Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

       Сформируем два результата, которые понадобятся далее.

Теорема 1. Пусть случайные величины 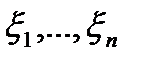 независимы и нормальны с параметрами (0, 1), тогда случайная величина  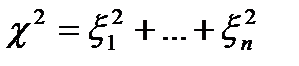подчинена закону распределения с плотностью вероятности

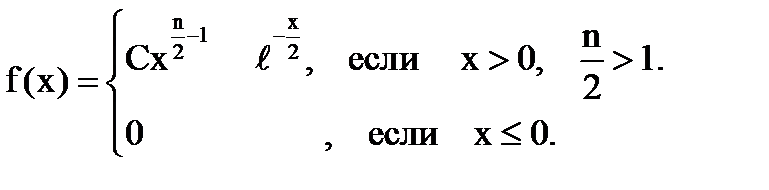
Где число n называется числом степеней свободы.

f(x)

0

x

 

Рис. 1. 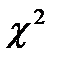 – распределение (Пирсона).

Теорема 2. Пусть случайные величины 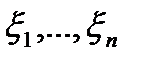 независимы и нормальны с параметрами (0, 1), тогда случайная величина  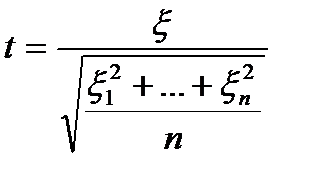подчинена закону распределения с плотностью вероятности:

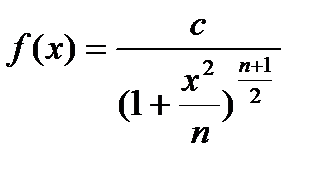
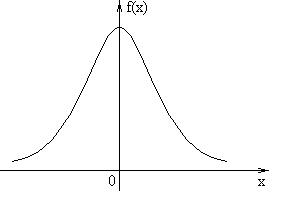
Рис. 2. t – распределение (Стьюдента).

 

       В обоих случаях константа С подобрана так, чтобы площадь под графиком плотности была равна 1.

 

       Квантиль распределения . Пусть имеется случайная величина 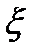 с функцией распределения F(x). Будем предполагать, что функция F(x) непрерывна и строго монотонна.

 

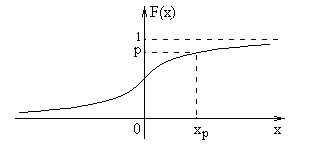
Рис. 3

Зададим число  pÎ (0, 1).

Квантилем уровня p распределения F ( x ) называется корень уравнения F(x) = p ,   х - ?

Обозначим его 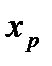 (см. рис. 3). Из определения функции F(x) вытекает: .

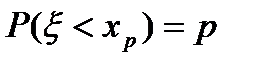Нам понадобится далее квантили распределений Пирсона и Стьюдента. Они обозначаются: ,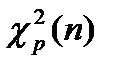

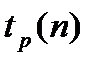
       Для этих квантилей имеются таблицы.

 

Доверительные интервалы для математического ожидания и дисперсии

       Пусть с испытанием связана случайная величина 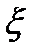 с неизвестными числовыми характеристиками (а, D) и пусть по выборке вычислены оценки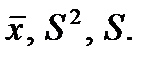

       Зададимся числом р в интервале (0,1).

Теорема. В указанной ситуации при достаточно большом объеме выборки с вероятностью р имеют место неравенства

        .

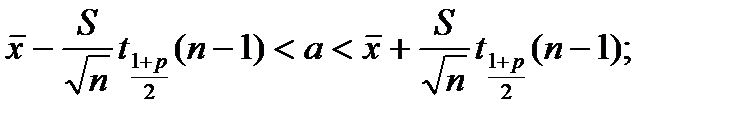
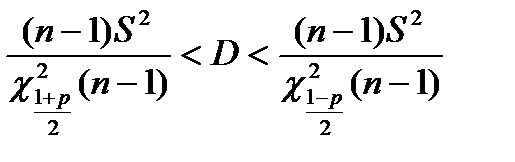Эти интервалы называются доверительными интервалами для математического ожидания и дисперсии. Число р называется уровнем доверия или доверительной вероятностью.

       Здесь n-объем выборки, 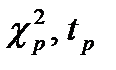-квантили распределений Пирсона и Стьюдента.

Указанные интервалы иногда называют интервальными оценками для математического ожидания и дисперсии.

Пример. Выполнена выборка значений случайной величины 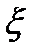 объема n = 25 и вычислены состоятельные несмещенные оценки для математического ожидания и

дисперсии: 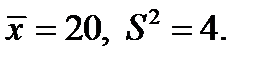 Найти доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0,95.

В силу неравенств (44), (45) с р = 0,95 имеют место интервальные оценки:

;

.

 

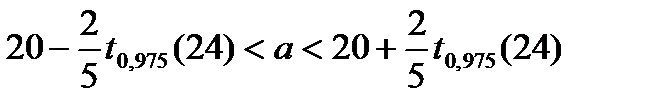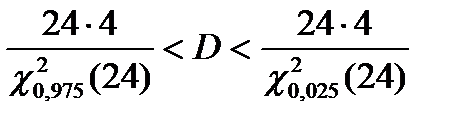По таблице квантилей (IV, V) найдем:

.

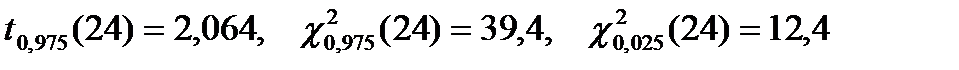Подставляя эти значения, получим: с вероятностью 0,95 верны неравенства: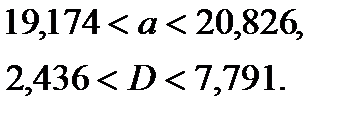

Лекция № 6

Тема: Проверка статистических гипотез

План:

1. Основные определения (статистическая гипотеза и примеры, классификация, ошибки 1-го и 2-го рода). Критерии согласия.

2. Параметрические гипотезы.

 

       Статистикой будем называть любую функцию 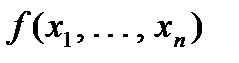 от выборки .

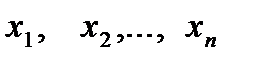Статистической называется гипотеза о предполагаемом виде неизвестного распределения или утверждение относительно значений одного или нескольких параметров известного распределения.

       Примеры статистических гипотез: генеральная совокупность наблюдаемых значений распределена по закону Пуассона, дисперсия двух нормальных совокупностей, равных между собой.

По содержанию статистические гипотезы можно классифицировать:

       1. Гипотезы о типе вероятностного закона распределения случайной величины, характеризующего явление или процесс.

       2. Гипотезы об однородности двух или более обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые выборочные характеристики различаются между собой статистически значимо или нет.

       3. Гипотезы о свойствах числовых значений параметров исследуемой генеральной совокупности. Больше ли значения параметров некоторого заданного номинала или меньше и т.д.

       4. Гипотезы о вероятностной зависимости двух или более признаков, характеризующих различные свойства рассматриваемого явления или процесса. При этом определяется характер этой зависимости.

Наряду с выдвинутой гипотезой рассматривают и противоположную ей. Если выдвинутая гипотеза будет отвергнута, то имеет место противоположная ей. По этой причине гипотезы делят на:

1. нулевые (основная);

2. конкурирующие (альтернативной).

 

       Гипотеза, которая подвергается проверке, называется нулевой и обозначается H₀. Альтернативной гипотезой H₁ (от Hypothesis – «гипотеза» (англ.)) называется гипотеза, конкурирующая с нулевой, т. е. ей противоречащая. Простой называется гипотеза, содержащая только одно предположение.

Кроме того гипотезы делят на простые и сложные. Простой называют гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез.несколько простых гипотез. Например гипотеза Н: 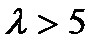 содержит бесчисленное множество простых гипотез Н_i: 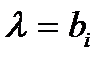,где 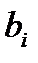-любое число большее 5.

Пример. Пусть проверяется гипотеза о равенстве некоторого параметра a значению a₀ , т. е. гипотеза H₀: a = a₀. В этом случае альтернативной гипотезой можно рассматривать одну из следующих гипотез:H₁: a > a₀; H₁: a < a₀; H₁: a ≠ a₀; H₁: a > 2. Все приведенные гипотезы простые, и только H₁: a > 2– сложная гипотеза.

 

Выбор альтернативной гипотезы определяется формулировкой решаемой задачи. Причина выделения нулевой гипотезы состоит в том, что чаще всего такие гипотезы рассматриваются как утверждения, которые более ценны, если они опровергаются. Это основано на общем принципе, в соответствии с которым теория должна быть отвергнута, если есть противоречащий ей факт, но не обязательно должна быть принята, если противоречащих ей фактов на текущий момент нет.

Правило, по которому выносится решение принять или отклонить гипотезу H₀, называется статистическим критерием. Проверка статистических гипотез осуществляется по результатам наблюдений (экспериментов, опытов), из которых формируют функцию результатов наблюдений, называемую проверочной статистикой. Таким образом, статистический критерий устанавливает, при каких значениях этой статистики проверяемая гипотеза принимается, а при каких она отвергается.

Правило проверки гипотезы о законе распределения:

1. Задаются уровнем значимости 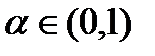 и вычисляют квантиль .

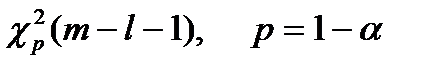2. Выполняют выборку 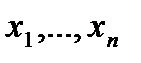 и по формуле вычисляют .

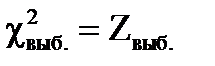3. Если 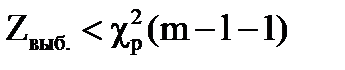, гипотеза принимается.

Если 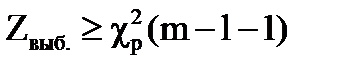, гипотеза отвергается.

 

При проверке гипотез по указанному правилу возможны ошибки двух типов:

1. Ошибка первого рода: отвергается верная гипотеза. Вероятность этой ошибки равна уровню значимости a. Действительно, из определения a имеем:

Р (ошибки 1-го рода)=

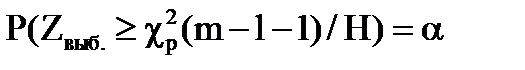
2. Ошибка второго рода: принимается неверная гипотеза. Вероятность этой ошибки обозначают b:

Р (ошибки второго рода)=  .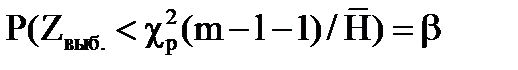

В конкретной ситуации эта вероятность может быть вычислена.

В математической статистике доказывается: при фиксированном объеме выборки уменьшение уровня значимости a влечет увеличение b и обратно, уменьшение b влечет увеличение a.

       Единственный способ уменьшения одновременно a и b - это увеличение объема выборки.

       В конкретных ситуациях можно минимизировать вероятность той ошибки, которая ведет к менее тяжелым последствиям. Рекомендуется, если это возможно, проводить проверку более одного раза (набрать хотя бы еще одну выборку).

       Мощностью критерия называется вероятность отвергнуть неверную гипотезу:

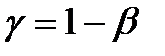, где b - вероятность ошибки второго рода.

Малое значение вероятности α, используемое при проверке гипотезы, называется уровнем значимости критерия. Интервал значений 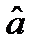, для которых гипотезу следует отвергнуть, называется областью отклонения гипотезы, или критической областью. Интервал значений 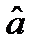, при которых гипотезу следует принять, носит название области принятия гипотезы (см. рис. 1).

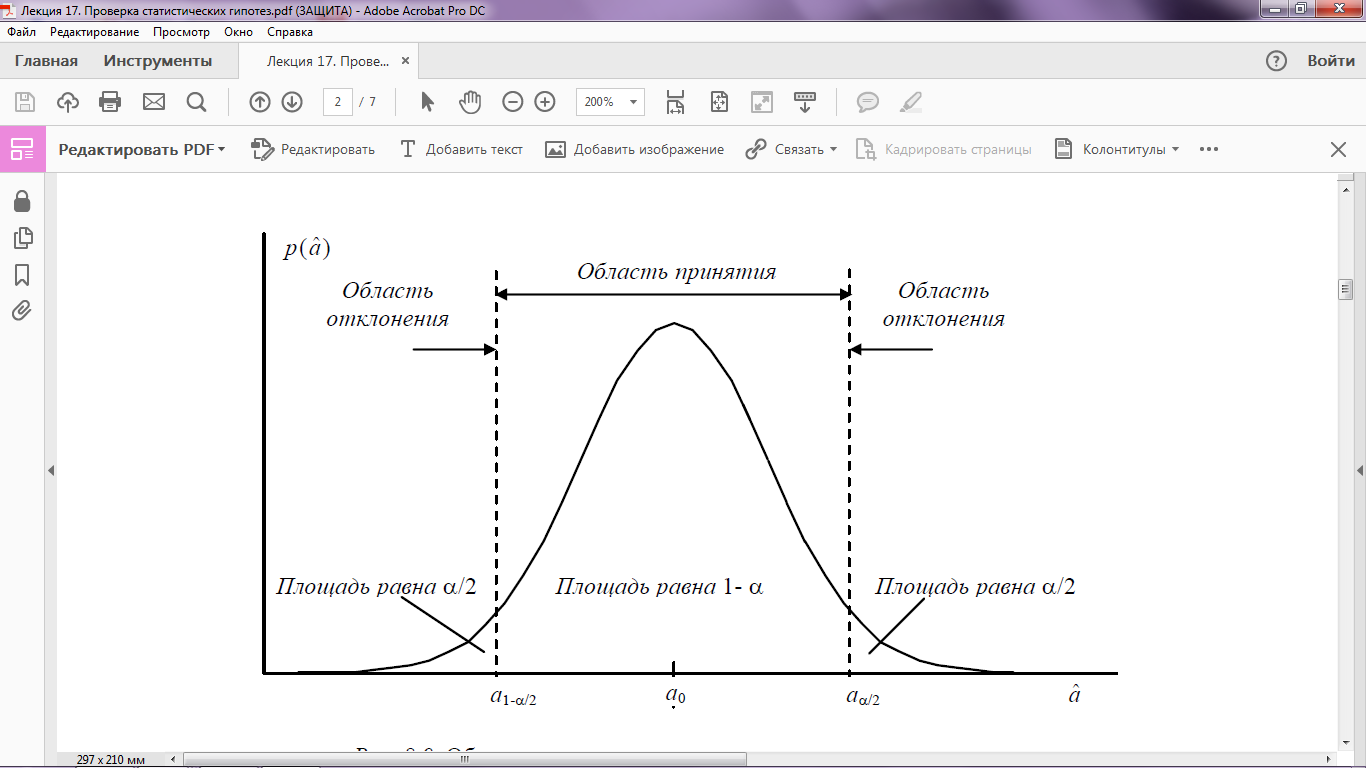
Рис.1. Области принятия и оклонения при проверке гипотез

 

Приведенный способ проверки гипотезы называется двусторонним критерием, так как если гипотеза H₀ верна, то величина 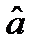 может быть как больше, так и меньше a₀. Необходимо проверять значимость расхождения между  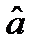и a₀ с обеих сторон. В некоторых задачах может оказаться достаточно одностороннего критерия.

Например, пусть гипотеза состоит том, что a ≥ a₀. В этом случае гипотеза будет ошибочной только тогда, когда a < a₀, а критерий будет использовать только нижнюю границу плотности распределения p( ).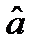

Как видно на рис. 1, ошибка первого рода происходит в том случае, когда при справедливости гипотезы 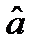 попадает в область ее отклонения. Таким образом, вероятность ошибки первого рода равна α, т. е. уровню значимости критерия.

Для того чтобы найти вероятность ошибки второго рода, следует определить каким-тообразом величину отклонения истинного значения параметра a от гипотетического значения параметра a₀, которое требуется определить. Предполагается, что истинное значение параметра a₀ в действительности равно a₀ + d или a₀ − d (см. рис. 2).

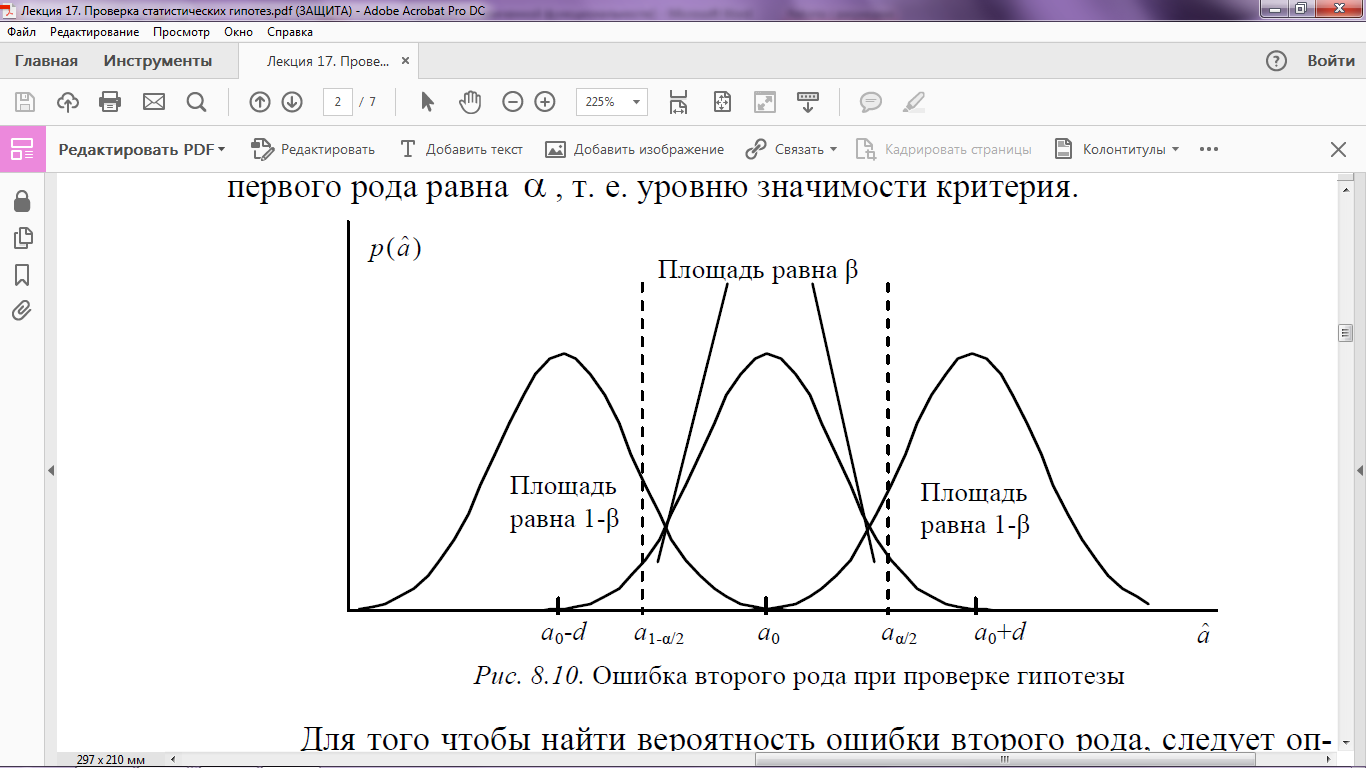
Рис.2. Ошибка второго рода при проверке гипотезы.

 

Если согласно гипотезе H₀: a = a₀, а на самом деле a = a₀ ± d, то вероятность того, что 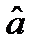 попадет в область принятия гипотезы H₀, т.е. в интервал (a_{1−α 2}, a_{α 2}), составляет β. Таким образом, вероятность ошибки второго рода равна β при выявлении отклонения истинного значения параметра a на ± d от гипотетической величины a₀.

 

       Под статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы.

Различают три вида критериев:

       1) Параметрические критерии - критерии значимости, которые служат для проверки гипотез о параметрах распределения генеральной совокупности при известном виде распределения.

       2) Критерии согласия - позволяют проверить гипотезы о соответствии распределений генеральной совокупности известной теоретической модели.

       3) Непараметрические критерии - используются в гипотезах, когда не требуется знаний о конкретном виде распределения.

 

       Задача проверки статистических гипотез сводится к исследованию генеральной совокупности по выборке. Множество возможных значений элементов выборки может быть разделено на два непересекающихся подмножества- критическую область и область принятия гипотезы.

       Наблюдаемые значения критерия (статистика) K_набл называют такое значение критерия, которое находится по данным выборки.

       Границы критической области, отделяющие ее от области принятия гипотезы, называют критическими точками и обозначают K_кр.

       Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают. Итак, процесс проверки гипотезы состоит из следующих этапов:

· выбирается статистический критерий К;

· вычисляется его наблюдаемое значение К_набл по имеющейся выборке;

· поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значение k_кр, разделяющее критическую область и область принятия гипотезы (например, если р(К > k_кр) = α, то справа от kкр располагается критическая область, а слева – область принятия гипотезы);

· если вычисленное значение Кнабл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.

Различают разные виды критических областей:

· правостороннюю критическую область, определяемую неравенством K > k_кр (k_кр > 0);

· левостороннюю критическую область, определяемую неравенством K < k_кр ( k_кр < 0);

· двустороннюю критическую область, определяемую неравенствами K < k₁, K > k₂ (k₂ > k₁).

Критерии согласия

       Критериями согласия называют критерии, в которых гипотеза определяет закон распределения либо полностью, либо с точностью до небольшого числа параметров. Существует несколько различных критериев согласия: критерий Смирнова, критерий Колмогорова, критерий χ²- Пирсона и др.

 

       Рассмотрим универсальный критерий согласия Пирсона. Проверка гипотезы о том, что эмпирическая частота мало отличается от соответствующей теоретической частоты, осуществляется с помощью величины χ²- меры расхождения между ними.

       Любая аналитическая функция f(x), с помощью которой аппроксимируется статистическое распределение, должна обладать основными свойствами плотности распределения:

f (x) ≥ 0

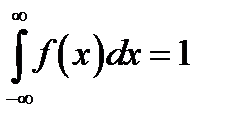
Чтобы оценить, насколько хорошо выбранный теоретический закон распределения согласуется с экспериментальными данными, используются так называемые критерии согласия. Таких критериев существует несколько, но наиболее часто применяется критерий согласия χ², предложенный Пирсоном. Является непараметрическим критерием проверки статистических гипотез.

Пусть проведено n независимых опытов, в каждом из которых случайная величина X приняла определенное значение. Результаты опытов сведены в k интервалов, и построены статистический ряд, выборочная функция распределения и гистограмма, т.е. экспериментальные данные описываются выборочным законом распределения P*(x). Необходимо проверить, согласуются ли экспериментальные данные с гипотезой H₀: P(x) = P*(x) о том, что случайная величина X имеет выбранный теоретический закон распределения P(x), который может быть задан функцией распределения F(x) или плотностью f(x). Альтернативная гипотеза в этом случае – H₁: P(x) ≠ P*(x).

Знание теоретического закона распределения позволяет найти теоретические вероятности попадания случайной величины в каждый интервал

(x_i, x_{i+ 1}), i = 1, k: p₁, p₂, K, p_k.

Проверка согласованности теоретического и статистического распределений сводится к оценке расхождений между теоретическими вероятностями p_i и полученными частотами p^*_i. В качестве меры расхождения удобно выбрать сумму квадратов отклонений(p^*_i  − p_i), взятых с некоторыми «весами» c_i:

 

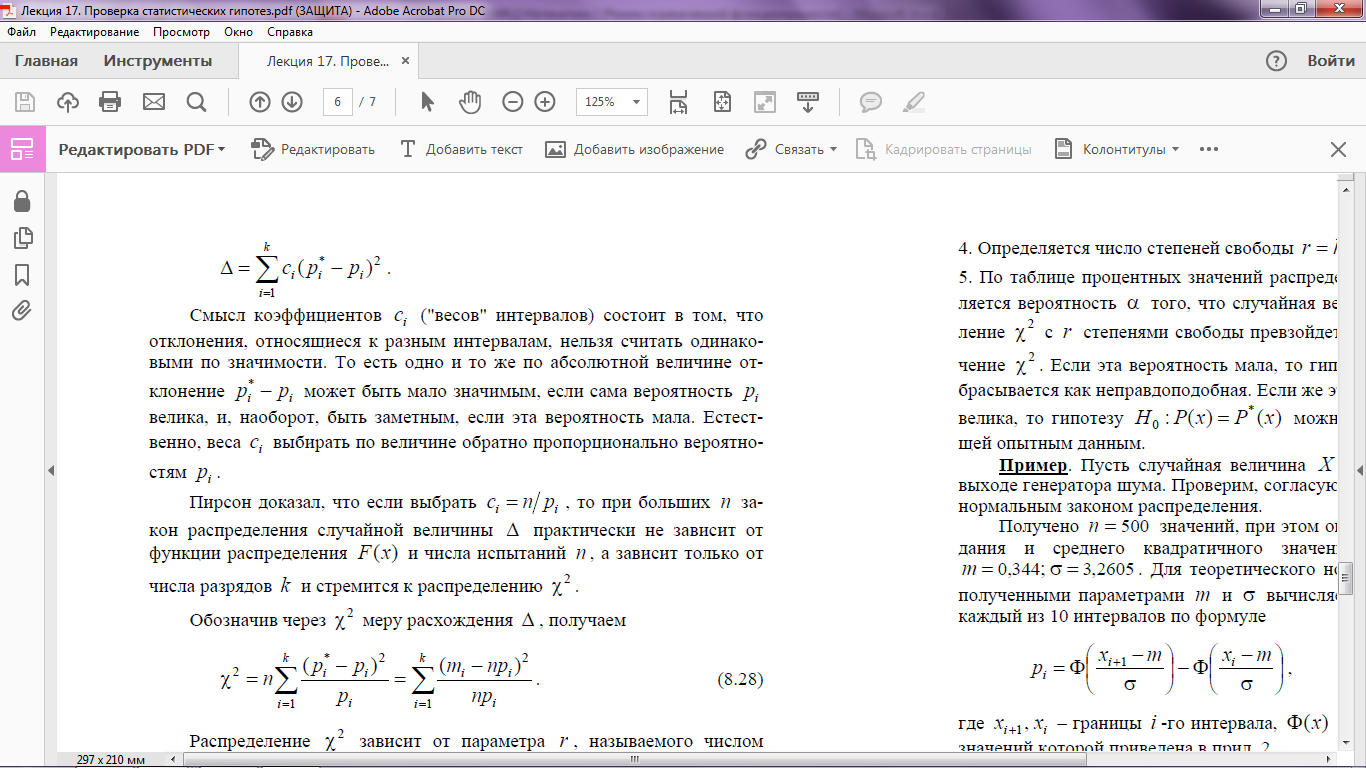
Смысл коэффициентов c_i («весов» интервалов) состоит в том, что отклонения, относящиеся к разным интервалам, нельзя считать одинаковыми по значимости. То есть одно и то же по абсолютной величине отклонение p^*_i  − p_i может быть мало значимым, если сама вероятность p_i велика, и, наоборот, быть заметным, если эта вероятность мала. Естественно, веса c_i выбирать по величине обратно пропорционально вероятностям p_i. Пирсон доказал, что если выбрать c_i = n/p_i, то при больших n закон распределения случайной величины практически не зависит от функции распределения F(x) и числа испытанийn, а зависит только от числа разрядов k и стремится к распределению χ². Обозначив через χ² меру расхождения , получаем:

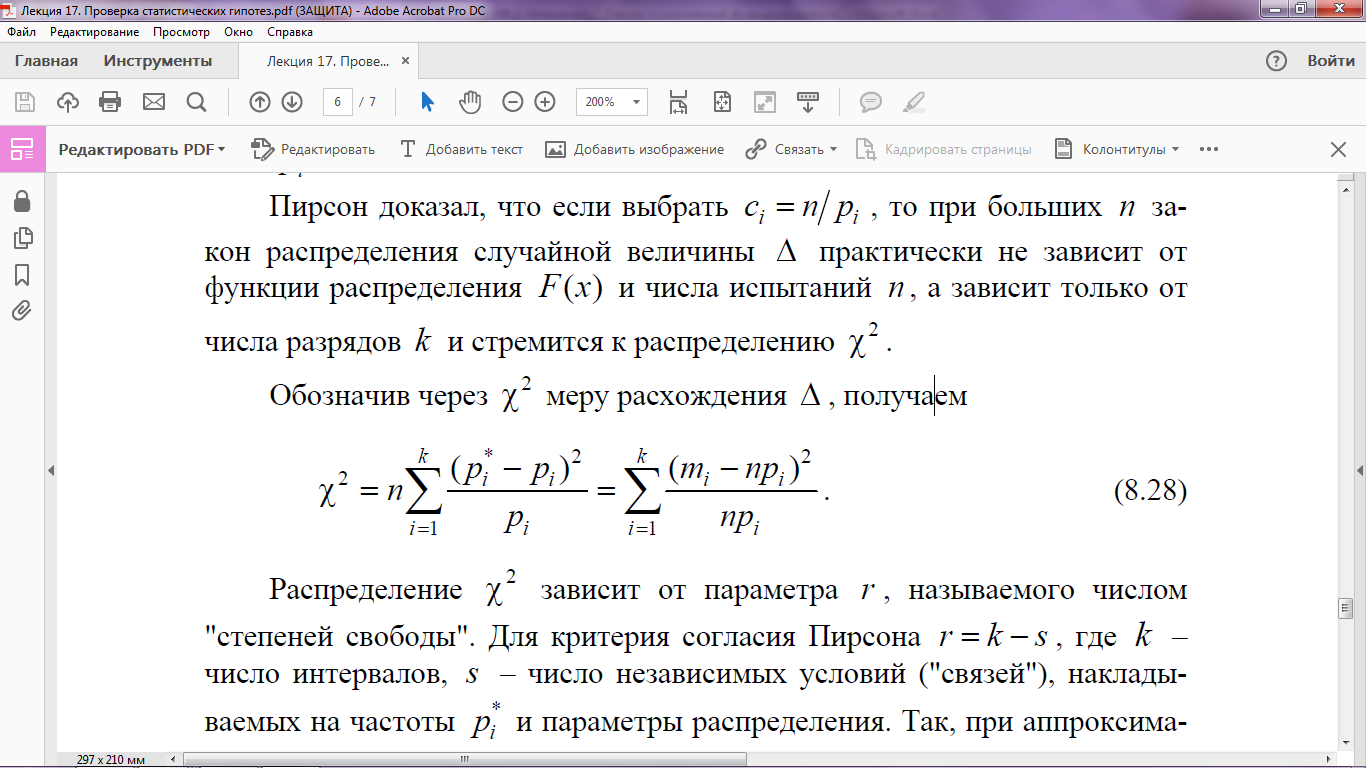
       Распределение зависит от параметра r, называемого числом степеней свободы, которое равно:

r = k − s,

где k – число интервалов, s – число независимых условий («связей»), накладываемых на частоты p* и параметры распределения. Так, при аппроксимации нормального распределения s = 3, а при исследовании распределения Пуассона s = 2.

       Схема применения критерия χ² для оценки согласованности теоретического и статистического распределения сводится к следующим процедурам (этапам):

       1. На основании полученных экспериментальных данных x₁, x₂, K, xnрассчитываются значения частот p^*_i в каждом из k интервалов.

       2. Вычисляются, исходя из теоретического распределения, вероятности p_i попадания значений случайной величины в интервалы(x_i, x_i + 1).

       3. По формуле   рассчитывается значение χ².

       4. Определяется число степеней свободы r = k − s.

       5. По таблице процентных значений распределения χ² определяется вероятность α того, что случайная величина, имеющая распределение χ² с r степенями свободы превзойдет полученное на этапе 3 значение χ². Если эта вероятность мала, то гипотеза H₀: P(x) = P*(x) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, то гипотезу H₀: P(x) = P*(x) можно признать не противоречащей опытным данным.

Пример. Пусть случайная величина X – значения напряжения на выходе генератора шума. Проверим, согласуются ли полученные данные с нормальным законом распределения.

Получено n = 500 значений, при этом оценки математического ожидания и среднего квадратичного значения соответственно равны: m = 0,344; σ = 3,2605. Для теоретического нормального распределения с полученными параметрами m и σ вычисляем вероятности попадания в каждый из 10 интервалов по формуле

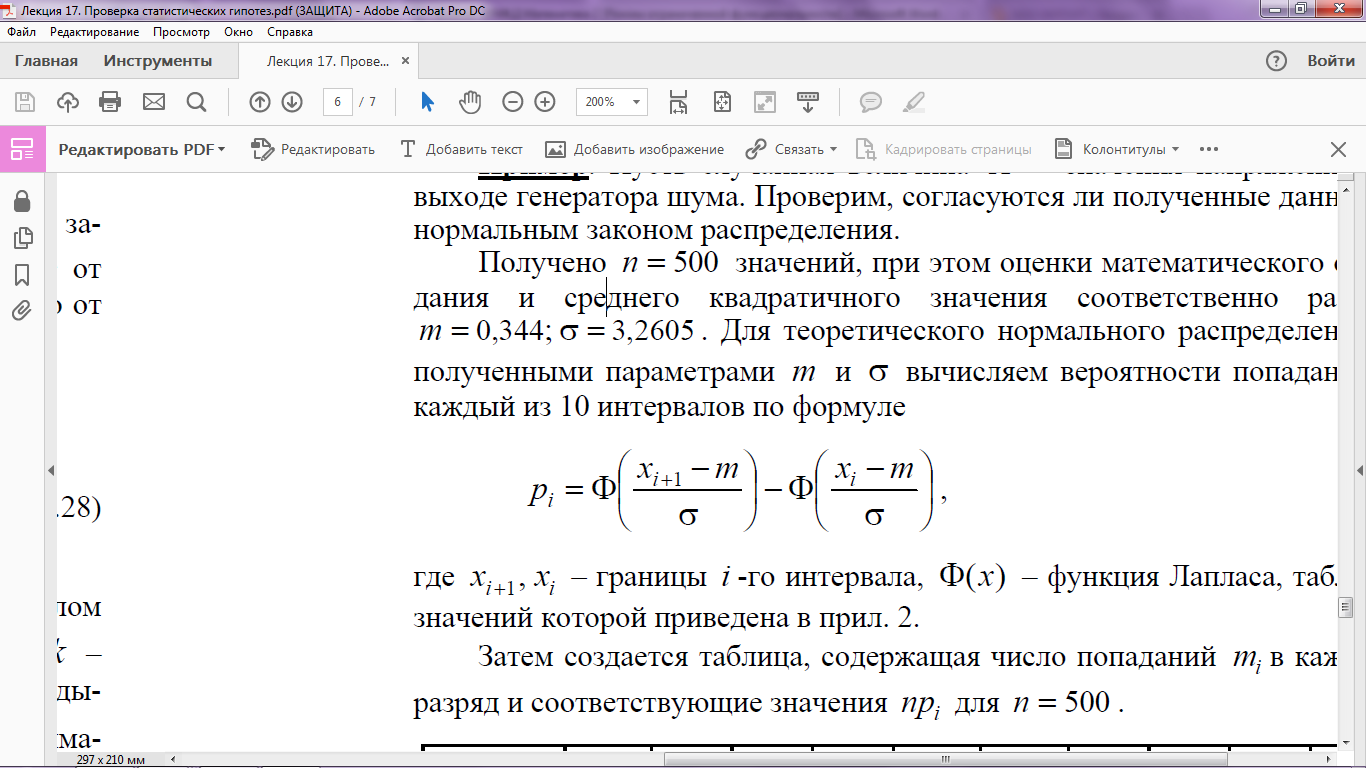
x_{i + 1}, x_i – границы i -гоинтервала,Φ(x) – функция Лапласа (табличная).

Затем создается таблица, содержащая число попаданий m i в каждый разряд и соответствующие значения npi для n = 500.

 

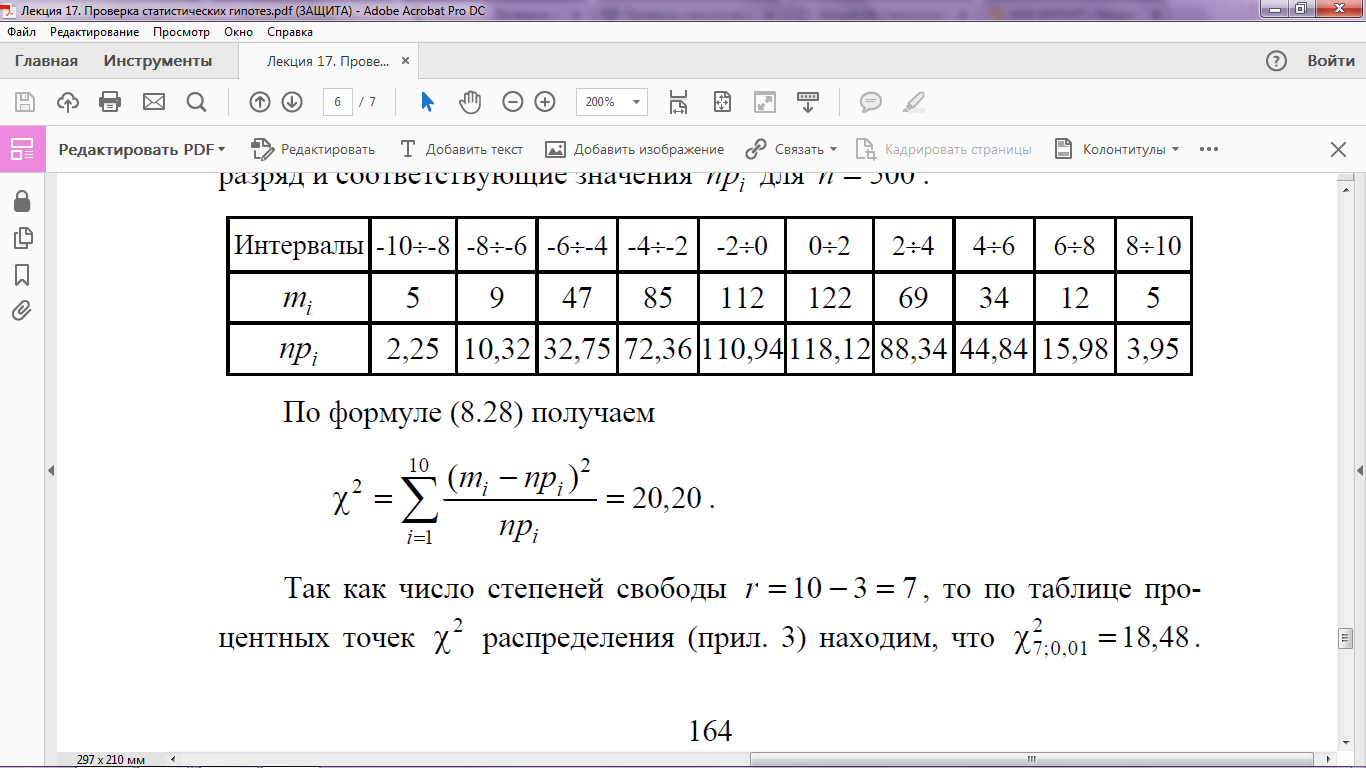
По формуле для χ²:

 

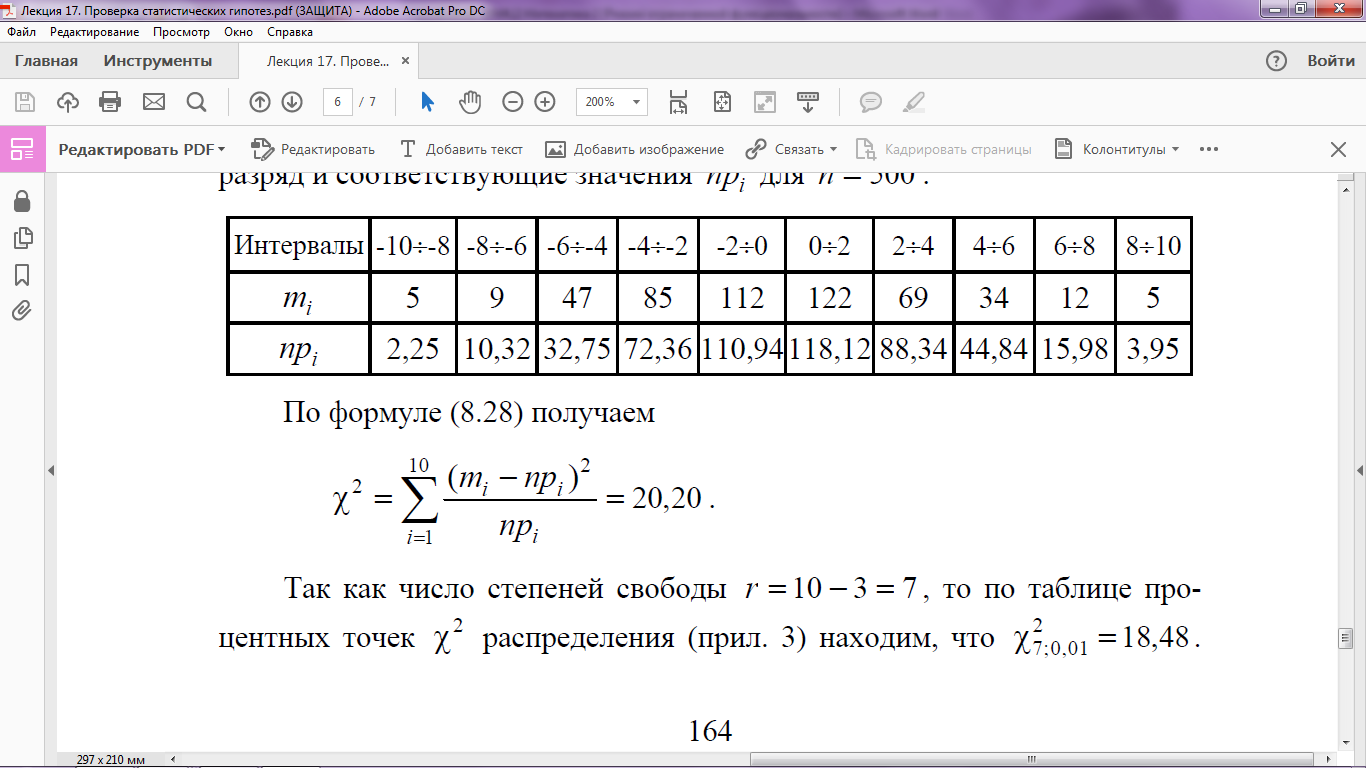
Так как число степеней свободы r = 10 − 3 = 7, то по таблице процентных точек χ² распределения находим, что χ²_{7; 0,01} = 18,48

       Поскольку χ² > χ²_7;0,01 для малой вероятности α = 0,01, следует признать: полученные экспериментальные данные противоречат проверяемой гипотезе о том, что случайная величина X распределена по нормальному закону.

       При использовании критерия согласия (χ² или любого другого) положительный ответ нельзя рассматривать как утвердительный о правильности выбранной гипотезы. Определенным является лишь отрицательный ответ, т.е. если полученная вероятность α мала, то можно отвергнуть выбранную гипотезу H₀: P(x) = P*(x) и отбросить ее как явно не согласующуюся с экспериментальными данными. Если же вероятность α велика, то это не может считаться доказательством справедливости гипотезы

H₀: P(x) = P*(x), а указывает только на то, что гипотеза не противоречит экспериментальным данным.

При использовании критерия согласия χ² достаточно большими должны быть не только общее число опытов n (несколько сотен), но и значения m_i в отдельных интервалах. Для всех интервалов должно выполняться условие m_i ≥ 5. Если для некоторых интервалов это условие нарушается, то соседние интервалы объединяются в один.

 

Схема применения критерия

       1. Выдвижение начальной гипотезы 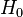, состоящей в том, что случайная величина X распределена по нормальному закону распределения.

       2. Необходимо сравнить эмпирические (найденные экспериментальным путем) и теоретические (найденные исходя из закона распределения) частот. Однако как бы точно не был подобран закон распределения между теоретическими и эмпирическими частотами неизбежны расхождения возникает вопрос, объяснимы ли эти расхождения только случайными факторами, связанные с ограниченным числом наблюдений, или это связано с неправильным выбором теоретического закона распределения. Критерий Пирсона позволяет ответить на этот вопрос, однако как и любой другой критерий, он не доказывает справедливости гипотез, а лишь устанавливает ее согласие или несогласие с экспериментальными данными на принятом уровне значимости. В качестве проверки нулевой гипотезы применяется случайная величина χ², которая вычисляется по формул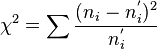е  где 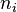 - эмпирические частоты,  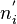- теоретические частоты.

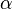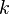       3. По таблице χ²-Пирсона находят критические значения χ², которое зависит от двух параметров  и , где 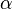 - заданный уровень значимости (обычно 0,05 0,01 0,1) (то есть с вероятностью 0,95 0,99 0,9 можно гарантировать принятие или опровержение гипотезы)  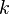- число степеней свободы. Оно находится по формул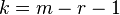е , где 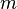 - число групп (интервалов в вариационном ряду),  - число параметров распределения (для нормального распределения 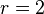, для показательного распределения 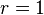, для равномерного )

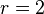       4. Необходимо сравнить χ² критическое и χ² наблюдаемое. Если χ² критическое больше χ² наблюдаемого, то гипотеза принимается, если χ² критическое меньше χ² наблюдаемого, то гипотеза опровергается.

       5. Сделать вывод из пункта 1.

Параметрические гипотезы.

       В тех случаях, когда известен закон, но неизвестны значения его параметров (дисперсия или математическое ожидание) в конкретной ситуации, статистическую гипотезу называют параметрической.

       Например, предположение об ожидаемом среднем доходе по акциям или разбросе дохода являются параметрическими гипотезами.

       Большинство параметрических методов разработаны для нормально распределенных совокупностей. Некоторые методы позволяют анализировать данные, распределенные по другим законам (например, биномиальному или Пуассона).

       Когда закон распределения генеральной совокупности не известен, но есть основания предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его распределения называются непараметрическими.

       Например, можно выдвинуть гипотезу, что число дневных продаж в магазине или доход населения подчинены нормальному закону распределения.

       Непараметрические методы позволяют исследовать данные без допущений о характере распределения переменных. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг, то эти тесты нечувствительны к выбросам. Непараметрические тесты могут применяться в тех случаях, когда переменные измерены при помощи порядковой или метрической шкалы. Существуют тесты, предназначенные для анализа номинальных данных.

       Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики. Когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью.

        Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), практически всегда подходят для больших выборок.

       Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство {F(x; θ), θ 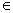Θ}, т.е. F(x) = F(x;θ₀) при некотором θ₀ 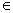Θ, то рассматриваемая гипотеза – параметрическая, в противном случае – непараметрическая.

       Если и H₀ и H₁ – параметрические гипотезы, то задача проверки статистической гипотезы – параметрическая. Если хотя бы одна из гипотез H₀ и H₁ – непараметрическая, то задача проверки статистической гипотезы – непараметрическая. Другими словами, если вероятностная модель ситуации – параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – параметрическая.

 

Традиционный метод проверки однородности двух независимых выборок (критерий Стьюдента)

       Наиболее распространенный метод проверки однородности выборок путем выдвижения и проверки параметрических гипотез основан на применении критерия Стьюдента.

       Рассмотрим случай сравнения двух независимых выборок.

       Выдвигаются: нулевая гипотеза о равенстве средних и альтернативная, о том, что средние не равны.

       Вычисляют выборочные средние арифметические и дисперсии в каждой выборке и статистику Стьюдента t, на основе которой принимают решение.

       По заданному уровню значимости a и числу степеней свободы (m + n - 2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t| > t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t| < t_кр, то принимают.

Общая постановка задачи проверки гипотез:

       1. Формулируют (выдвигают) нулевую гипотезу H₀ об отсутствии различий между группами, об отсутствии существенного отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др.

Сущность нулевой гипотезы H₀: разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, то есть эти выборки принадлежат одной генеральной совокупности.

       2. Формулируют противоположную нулевой, альтернативную гипотезу H₁.

       3. Задают уровень значимости α. Уровень значимости α – это вероятность ошибки отвергнуть нулевую гипотезу H₀, если на самом деле эта гипотеза верна. При α ≤ 0,05 ошибка возможна в 5% случаев.

       4. Для проверки выдвинутой гипотезы используют критерии.

       Критерий – это случайная величина К. которая служит для проверки H₀. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости α. Фактическую величину критерия получают по данным наблюдения К_набл.

       5. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно К_крит(α, f).

       6. Сравнивают Кнабл и К_крит(α, f).

Если К_набл > К_крит(α, f), то отвергают H₀ и принимают H₁.

Если К_набл < К_крит(α, f) то принимают H₀.

Это для параметрических критериев.

Если использованы непараметрические критерии, то наоборот: если К_набл > К_крит(α, f), то принимают H₀.

       7. Вывод: различие статистически значимо (α ≤ 0,05) или незначимо.

 

       Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности. Из которых взяты выборки, подчиняются нормальному закону распределения.

       Непараметрические критерии применяются, если нет подчинения распределения нормальному закону. Эти критерии обычно заменяют данные выборки знаками (+ или -), рангами (т.е. числами 1; 2; 3;…, описывающими их положение в упорядоченном наборе данных), категориями и т.п. Непараметрический критерий можно использовать, если объем выборки небольшой настолько, что невозможно оценить закон распределения данных.

 

Лекция № 7

Тема: Математическая формулировка экономических и производственных задач

План:

1. Представление ограничений ресурсов, капиталовложений и т.д. в виде линейных неравенств.

2. Определение функции цели и нахождение вектора решений, удовлетворяющего задаче с заданными ограничениями.