Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

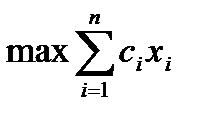
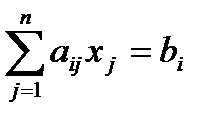, i=1,…, m,

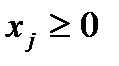, j=1,…, n.

       Основные вычислительные методы решения задач линейного программирования разработаны именно для канонической задачи.

 

Общая задача линейного программирования

       Необходимо максимизировать (минимизировать) линейную функцию от n переменных:

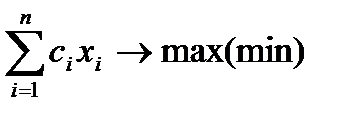
при ограничениях:

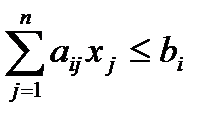, i=1,…, k, 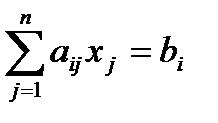, i=1+ k,…, m,  , …,   

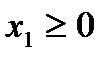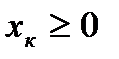
       Стандартная задача получается как частный случай общей при k =m, r = n; каноническая – при k = 0, r = n.

 

       Пример. Кондитерская фабрика производит несколько сортов конфет. Назовем их условно "A", "B" и "C". Известно, что реализация десяти килограмм конфет "А" дает прибыль 90 рублей, "В" - 100 рублей и "С" - 160 рублей. Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной. Нормы расхода сырья на производство 10 кг конфет каждого вида приведены в таблице 1.

 

Таблица 1. Нормы расходов сырья на производство

Сырье

Нормы расхода сырья

Запас сырья

А В С Какао 18 15 12 360 Сахар 6 4 8 192 Наполнитель 5 3 3 180 Прибыль 90 100 160 максимум Объем выпуска Х1 Х2 Х3  

 

Экономико-математическая формулировка задачи имеет вид: Найти такие значения переменных Х = (х₁, х₂, х₃), чтобы целевая функция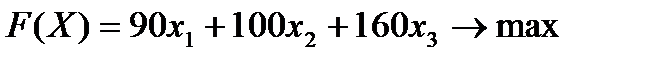

 при условиях-ограничениях:

 

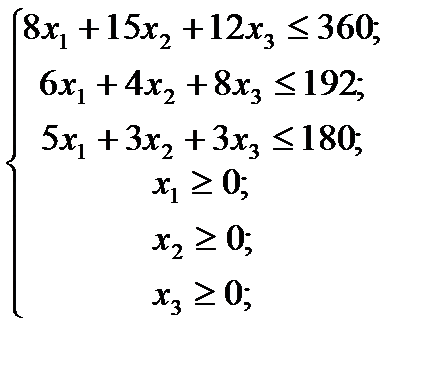
       Оптимизационная модель - экономико-математическая модель, которая охватывает некоторое число вариантов производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них. Кроме системы ограничений включает критерий для выбора, особое уравнение, называемое целевой функцией. С помощью такого критерия находят решение, наилучшее по какому-либо показателю, напр. минимум затрат на материалы при заданном объеме продукции или, максимум прибыли при заданных ограничениях по ресурсам и т. д.

       Оптимизационная модель является основным инструментом экономико-математических методов. Оптимизационные модели разного характера часто сводятся к задачам линейного программирования.

   Среди линейных моделей математического программирования особое место занимают четыре типа моделей:

1) модель общей задачи линейного программирования;

2) модель транспортной задачи линейного программирования;

3) модель распределительной задачи линейного программирования;

4) модель ассортиментной задачи линейного программирования.

   Модель общей задачи линейного программирования применяют для решения задач планирования в торговле, использования сырья, определения оптимального плана выпуска изделий и др.

   В торговле планирование связано с поиском наиболее выгодного варианта распределения различного вида ресурсов: финансовых, трудовых, товарных, материальных, технических и др. Модель общей задачи линейного программирования применяют для решения широкого круга задач торговой практики, таких как планирование товарооборота; организация рациональных за­купок продуктов питания (задача о диете); замена торгового оборудования; определение ассортимента товаров для торговой базы в силу ограниченной площади хранения; установление рационального режима работы и т.д.

       Методика построения экономико-математической модели заключается в том, чтобы экономическую сущность задачи представить математически. Необходимо определить систему переменных величин. Рассчитать нужные технико-экономические коэффициенты и собрать соответствующие нормативные данные. Все условия задачи записать в виде уравнений или неравенств. Обосновать критерии оптимальности и выразить его математической формулой.

Как правило, выделяется шесть этапов:

· постановка экономической проблемы (задачи), ее качественный анализ и обоснование критерия оптимальности;

· формализация экономической проблемы и ее математическая запись;

· подготовка исходной информации и технико-экономических коэффициентов;

· построение математической модели;

· создание расчетной компьютерной модели и ее решение;

· анализ результатов решения и их практическое применение.

 

       В настоящее время множество задач планирования и управления в различных отраслях хозяйства решаются методами математического программирования (моделирования), наиболее развитым из которых в области оптимизационных задач является самый простой и доступный метод линейного программирования (МЛП). Этот метод позволяет описать широкий круг задач хозяйственной и коммерческой деятельности: планирование товароснабжения, распределение ресурсов, капиталовложений, организация рациональных перевозок товаров, распределение рабочей силы и специалистов и т.д.

       Если задача МП содержит только линейные функции, то ее называют задачей линейного программирования.