Отнесение какого-либо объекта к некоторому классу в условиях упорядоченности классов решений (первый класс лучше второго и т.д.) и порядковых шкал оценок критериев накладывает определенные ограничения на отношения между объектами. Так, объекты, доминирующие по критериальным оценкам над данным объектом, не могут быть отнесены к классу, худшему, чем класс данного объекта. С другой стороны, объекты, над которыми он доминирует, не могут быть отнесены к классу, лучшему, чем класс данного объекта. Нарушение этих ограничений считалось ошибкой, допускаемой испытуемым при классификации.
Поведение испытуемых оценивалось по трем параметрам, смысл которых следует объяснить более подробно.
1. Число противоречий. Задача испытуемых состояла в разделении объектов (сочетаний оценок по критериям) на упорядоченные классы. На рис. 7.1,а приведен крайне простой вариант этой задачи - разделение на два класса (первый класс лучше второго) сочетаний оценок по двум критериям: А и В (первые оценки - лучшие; оценки на шкалах упорядочены по качеству). На рис. 7.1,а представлено гипотетическое разделение на два класса (пустые клетки — первый класс, заштрихованные — второй класс). Очевидно, что оценка клетки А2В2 противоречит оценкам клеток A 2 B 3, А3В2, A 4 B 2 и А3В3. Следовательно, в данной классификации на рис. 7.1,а имеются четыре противоречия.
2. Число замен (ошибок). Наряду с числом противоречий информативным является и другой показатель - число изменений в ответах испытуемого, которые делают классификацию непротиворечивой. Так, в классификации, представленной на рис. 7.1,а, нужно только одно изменение — назначение другого (первого) класса для сочетания А2В2. Эта замена делает классификацию непротиворечивой. Число замен характеризует число ошибок, совершенных испытуемыми при классификации.
3. Сложность границ между классами. Этот критерий, предложенный нами ранее [19], оценивает сложность правил, используемых при классификации. Так, граница между классами на рис. 7.1,6 очень проста, поскольку испытуемый фактически заменил критерии на ограничения. Его решающее правило в данном случае очень просто: к первому классу относятся сочетания, имеющие оценки лучшие, чем a 5 и лучше, чем B 4 .
Граница между классами на рис. 7.1,а значительно сложнее. Легко убедиться, что она описывается пятью сочетаниями оценок по двум критериям. Замена критерия на ограничения может происходить по двум причинам.
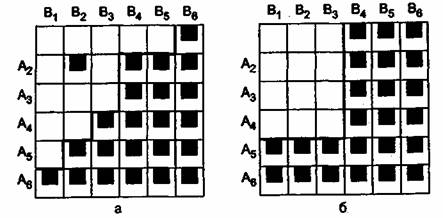
Рис.7.1. Сложное (в) и простое (б) разделение на два класса сочетаний оценок по двум критериям: А и В
Во-первых, среди испытуемых могут быть люди, которые рассматривают исходную задачу не как многокритериальную, а как более простую — однокритериальную с ограничениями по другим критериям (недаром А. Тверский [8] и Д. Рассо [11] предварительно отбирали испытуемых, использующих все критерии).
Во-вторых, как мы увидим далее, один и тот же человек может перейти к использованию ограничений вместо критериев при усложнении задачи. Известно, что стратегия последовательного введения ограничений вместо критериев («исключение по аспектам») в когнитивном отношении крайне проста.
В соответствии с вышеописанными критериями был установлен уровень требований к качеству выполнения задания, в соответствии с которым выносилось суждение о том, справился ли испытуемый с задачей классификации. Известно, что, выполняя те или иные операции по переработке информации, человек может ошибаться. Однако ошибка ошибке рознь. Как показано на рис. 7.1,а, ошибки, совершаемые вдали от границ, влекут за собой большое число противоречий. Эти ошибки, как правило, очевидны. Они не мешают установить границы между классами решений. Иначе обстоит дело с ошибками, совершаемыми у самой границы. Так, если испытуемый отнес ко второму классу клетку А2В3 на рис. 7.1,а, то имеется лишь одно противоречие (принадлежность клетки А3В3 к первому классу), и вопрос ставится следующим образом: отнести клетку А2В3 к первому классу или клетку А3В3 ко второму классу. Следовательно, ошибки около границы и на самой границе особенно опасны тем, что они меняют границу между классами, и при большом числе таких ошибок невозможно установить четкие границы между классами решений.
В связи с этим в качестве значения первого критерия, определяющего, справился ли испытуемый с задачей, было принято число ошибок, совершаемое около границы - на единичном расстоянии от границы (изменение на одну оценку по любому критерию переводит сочетание в элемент границы). Было принято, что испытуемый справляется с задачей лишь в том случае, когда число таких ошибок у границ между классами не превышает двух. В качестве второго критерия, определяющего, справился ли испытуемый с задачей классификации, была выбрана сложность границы, отражающая сложность решающих правил, используемых испытуемыми. А именно: требовалось, чтобы среди граничных элементов между классами были хотя бы один-два элемента, представляющих сочетания оценок критериев. Иначе говоря, считалось, что если испытуемый перевел все критерии в ограничения и превратил задачу в «исключение по аспектам», то он не справился с задачей. Действительно, в последнем случае задача многокритериальной классификации просто исчезает.
Описание экспериментов
Следует разделить эксперименты на две группы: 1) эксперименты, проводимые с людьми, не имевшими большой практики в принятии решений (студенты, школьники - первая серия экспериментов),
2) эксперименты, где в качестве испытуемых выступали профессионалы, решающие реальные практические задачи (вторая серия экспериментов).
Для первой группы испытуемых имелись широкие возможности варьировать параметры задачи классификации и условия эксперимента. Студенты (эксперименты с 1-го по 12-й) классифицировали арендуемые квартиры, решая, насколько предлагаемые варианты удовлетворяют их, а школьники (эксперименты 13 и 14) - высшие учебные заведения, определяя насколько они подходят им для поступления после окончания школы. Для второй группы испытуемых возможности варьирования параметров задачи почти отсутствовали, и схема эксперимента соответствовала реальной задаче. В экспериментах второй серии участвовали члены редакционного совета научно-исследовательского института, оценивая качество предлагаемых к опубликованию препринтов (эксперименты 15 и 16).
Результаты экспериментов
Данные о среднем количестве ошибок, допускаемых испытуемыми при выполнении 100 классификаций в каждом из экспериментов, представлены в табл. 7.1.
Как видно из таблицы, среднее число ошибок зависит от сложности задачи классификации. Можно определить зависимость количества ошибок от параметров Р, N и W . Это позволило получить следующий результат: число ошибок (число замен) при фиксированных N и W существенно зависит от числа классов решений Р.
Среднее время, затрачиваемое испытуемыми на вынесение одного суждения о принадлежности объекта к тому или иному классу, составляло 14 с. Дополнительный анализ качества выполнения классификации, проведенный для каждого испытуемого в соответствии с критериями, позволил вынести суждение, справился ли испытуемый с заданием. Например, в эксперименте 9, при N=4 (число критериев), Wi =4, i =1,...,4 (число оценок на порядковых шкалах), Р=2 (число классов решений), 67% испытуемых справились с задачей (среднее число ошибок равнялось 3). В эксперименте 7, при тех же N=4 и W =4, но уже при Р=4, не справились с задачей 90% испытуемых, причем наблюдалось резкое увеличение числа противоречий и ошибок (среднее число замен равнялось 8,8).
Были найдены такие значения N , W , Р, что при увеличении одного из этих параметров значительная часть испытуемых переставала справляться с задачей. Было условно определено, что если как минимум треть испытуемых из группы, состоявшей обычно из 10-15 человек, успешно справляется с задачей, то задача классификации данной сложности находится в пределах возможностей человека.
Таблица 7.1 Результаты экспериментов по решению задачи классификации многомерных объектов
| Номер эксперимента | Количество испытуемых | Размерность задачи | Среднее число допущенных ошибок | Процент испытуемых, справившихся с задачей | ||||
| N | W | P | Q | |||||
| 1 | 9 | 7 | 2 | 5 | 128 | 9,5 | 11 | Первая серия экспериментов |
| 2 | 9 | 7 | 2 | 4 | 128 | 6,5 | 0 | |
| 3* | 19 | 7 | 2 | 3 | 128 | 6,5 | 37 | |
| 4 | 15 | 5 | 3 | 4 | 243 | 9,7 | 13 | |
| 5* | 20 | 5 | 3 | 3 | 243 | 5,8 | 35 | |
| 6* | 24 | 5 | 3 | 2 | 243 | 5,0 | 46 | |
| 7 | 20 | 4 | 4 | 4 | 256 | 8,8 | 10 | |
| 8 | 20 | 4 | 4 | 3 | 256 | 6,2 | 20 | |
| 9* | 9 | 4 | 4 | 2 | 256 | 3 | 67 | |
| 10 | 10 | 3 | 5 | 5 | 125 | 17 | 0 | |
| 11 | 11 | 3 | 5 | 4 | 125 | 8,8 | 9 | |
| 12* | 10 | 3 | 5 | 3 | 125 | 5,1 | 60 | |
| 13 | 16 | 5 | 3 | 4 | 243 | 9,8 | 19 | |
| 14* | 16 | 5 | 3 | 2 | 243 | 3,5 | 73 | |
| 15* | 9 | 5 | 3 | 2 | 243 | 3,3 | Вторая серия экспериментов | |
| 16 | 4 | 5 | 3 | 4 | 243 | 1,3 | ||
| Примечание: N-число критериев; W-число градаций на шкалах их оценок; P-число классов; Q-число классифицируемых объектов; *-сложность данной задачи находится в пределах возможностей человека | ||||||||
Дата: 2019-02-19, просмотров: 386.