Двухфакторный дисперсионный анализ с повторениями применяется для того, чтобы проверить не только возможную зависимость результативного признака от двух факторов - A и B, но и возможное взаимодействие факторов A и B. Тогда a - число градаций фактора A и b - число градаций фактора B, r - число повторений. В статистическом комплексе сумма квадратов остатков разделяется на четыре компоненты:

SS = SS_a + SS_b + SS_ab + SS_e,

где

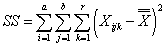- общая сумма квадратов отклонений,

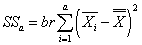- объяснённая влиянием фактора A сумма квадратов отклонений,

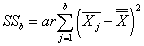- объяснённая влиянием фактора B сумма квадратов отклонений,

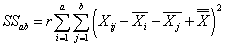- объяснённая влиянием взаимодействия факторов Aи B сумма квадратов отклонений,

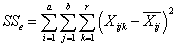- необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки,

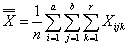- общее среднее наблюдений,

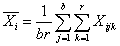- среднее наблюдений в каждой градации фактора A,

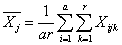- среднее число наблюдений в каждой градации фактора B,

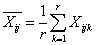- среднее число наблюдений в каждой комбинации градаций факторов A и B,

n = abr - общее число наблюдений.

Дисперсии вычисляются следующим образом:

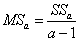- дисперсия, объяснённая влиянием фактора A,

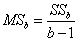- дисперсия, объяснённая влиянием фактора B,

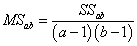- дисперсия, объяснённая взаимодействием факторов A и B,

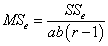- необъяснённая дисперсия или дисперсия ошибки,

где

v_a = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,

v_b = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,

v_ab = (a − 1)(b − 1) - число степеней свободы дисперсии, объяснённой взаимодействием факторов A и B,

v_e = ab(r − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,

v = abr − 1 - общее число степеней свободы.

Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются три нулевые гипотезы и соответствующие альтернативные гипотезы:

для фактора A:

H₀: μ₁A = μ₂A = ... = μ_aA,

H₁: не все μ_iA равны;

для фактора B:

H₀: μ₁B = μ₂B = ... = μ_aB,

H₁: не все μ_iB равны;

для взаимодействия факторов A и B:

H₀: AB_ij = 0,

H₁: AB_ij ≠ 0 для всех i и j.

Чтобы определить влияние фактора A, нужно фактическое отношение Фишера 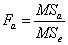сравнить с критическим отношением Фишера .

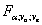Чтобы определить влияние фактора B, нужно фактическое отношение Фишера 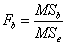сравнить с критическим отношением Фишера .

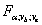Чтобы определить влияние взаимодействия факторов A и B, нужно фактическое отношение Фишера 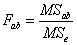сравнить с критическим отношением Фишера .

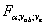Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.

Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.

Пример 4.

Торговое предприятие имеет три магазина - A, B и C. Проводятся две рекламные кампании. Требуется выяснить, зависят ли средние дневные доходы магазинов от двух рекламных кампаний. Для процедуры проверки случайно выбраны по 3 дня каждой рекламной кампании (то есть число повторений r = 3). Результаты обобщены в таблице:

Рекламная кампания	Магазин A	Магазин B	Магазин C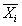
Рекламная кампания 1	12,05	15,17	9,48	14,53
	23,94	18,52	6,92
	14,63	19,57	10,47
Рекламная кампания 2	25,78	21,40	7,63	15,86
	17,52	13,59	11,90
	18,45	20,57	5,92
Среднее	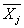18,73	18,14	8,72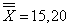

Факторы, подлежащие проверке: магазин (A, B и C) и рекламная кампания (1 и 2). Пусть эти факторы не зависят друг от друга.

Вычислим суммы квадратов отклонений:

SS = 592,47

SS_a = 8,01,

SS_b = 378,38,

SS_ab = 13,85,

SS_e = 192,22.

Числа степеней свободы:

v_a = a − 1 = 2 − 1 = 1,

v_b = b − 1 = 3 − 1 = 2,

v_ab = (a − 1)(b − 1) = 2,

v_e = ab(r − 1) = 12,

v = abr − 1 = 17.

Дисперсии:

,

,

,

.

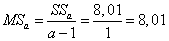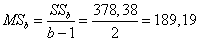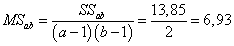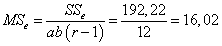Фактические отношения Фишера:

для фактора A: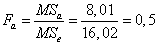

для фактора B: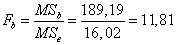

для взаимодействия факторов A и B: .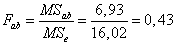

Критические значения отношения Фишера:

для фактора A: ,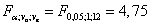

для фактора B: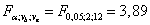

для взаимодействия факторов A и B: .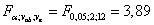

Делаем выводы:

о влиянии фактора A: фактическое отношение Фишера меньше критического значения, следовательно, рекламная кампания существенно не влияет на дневные доходы магазина с вероятностью 95%,

о влиянии фактора B: фактическое отношение Фишера больше критического, следовательно, доходы существенно различаются между магазинами,

о взаимодействии факторов A и B: фактическое отношение Фишера меньше критического, следовательно, взаимодействие рекламной кампании и конкретного магазина не существенно.