Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Занятие 5.

 ДИСПЕРСИОННЫЙ АНАЛИЗ

1. Однофакторный дисперсионный анализ. 1

Пример 1. 3

2 Двухфакторный дисперсионный анализ. 4

Пример  2. 5

3 Двухфакторный дисперсионный анализ без повторений в MS Excel. 6

Пример 3. 6

4 Двухфакторный дисперсионный анализ с повторениями.. 8

Пример 4. 10

5 Двухфакторный дисперсионный анализ с повторениями в MS Excel. 12

6 Практические задания. 13

6.1 Однофакторный ДА.. 13

Задание 1. 14

Задание 2. 14

Задание 3. 14

Задание 4. 15

6.2 Двухфакторный дисперсионный анализ без повторений. 15

Задание 5. 15

Задание 6. 15

6.3 Двухфакторный дисперсионный анализ с повторением.. 16

Задание 7. 16

Задание 8. 16

Пример 1.

Необходимо выявить, влияет ли расстояние от центра города на степень заполняемости гостиниц. Пусть введены 3 уровня расстояний от центра города: 1) до 3 км, 2) от 3 до 5 км и 3) свыше 5 км. Данные заполняемости представлены в таблице.

Решение.

1. Исследуемые данные введите в рабочую таблицу Excel по столбцам: в столбец А — заполняемость гостиниц в центре города, в столбец  В— гостиниц, находящихся на расстоянии от 3 до 5 км и т. д. (диапазон А1:С6).

2. Выполните команду Сервис > Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа щелчком мыши выберите процедуру Однофакторный дисперсионный анализ. Нажмите кнопку ОК.

3. В появившемся диалоговом окне Однофакторный дисперсионный анализ в поле Входной интервал задайте А 1: С 6. Для этого наведите указатель мыши на ячейку А1 и протяните его к ячейке С6 при нажатой левой кнопке мыши.

4. В разделе Группировка переключатель установите в положение по столбцам.

5. Далее необходимо указать выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем щелкните указателем мыши в правом поле ввода Выходной интервал, и щелчком мыши на ячейке А8 укажите расположение выходного диапазона. Нажмите кнопку ОК.

Результаты анализа. В результате будет получена таблица

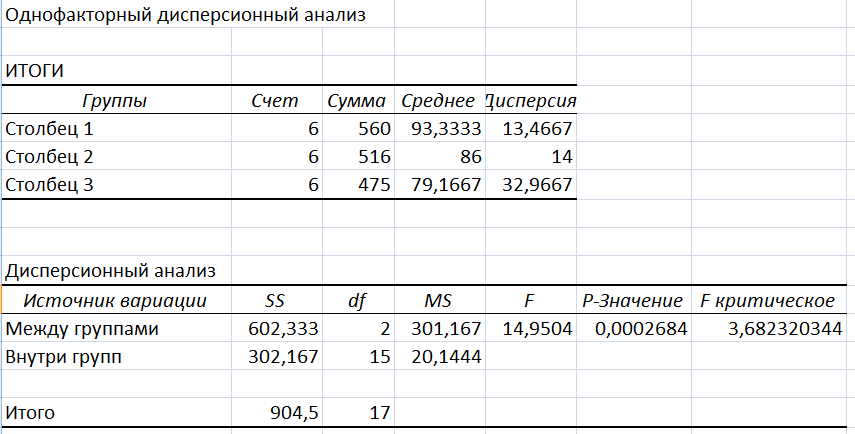
Результат работы инструмента Однофакторный дисперсионный анализ

 

Интерпретация результатов.

В таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение находится величина 0,0002684. Величина Р-Значение < 0,05, следовательно, критерий Фишера значим и влияние фактора расстояния от центра города на эффективность заполнения гостиниц доказано статистически.

Пример  2.

Дана информация о среднем потреблении топлива на 100 километров в литрах в зависимости от объёма двигателя и вида топлива.

	Бензин со свинцом	Бензин без свинца	Дизельное топливо	Среднее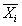
1001-1500 см³	9,3	8,9	6,5	8,23
1501-2000 см³	9,4	9,1	7,1	8,53
Более 2000 см³	12,6	9,8	8,0	10,13
Среднее	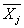10,42	9,27	7,2

 

Требуется проверить, зависит ли потребление топлива от объёма двигателя и вида топлива.

Решение.

Для фактора A число классов градации a = 3, для фактора B число классов градации b = 3.

Вычисляем суммы квадратов отклонений:

,

,

,

.

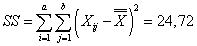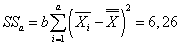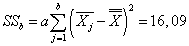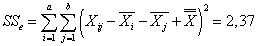Соответствующие дисперсии:

,

,

.

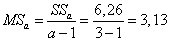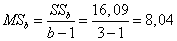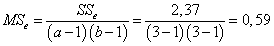Фактическое отношение Фишера для фактора A 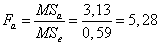, критическое значение отношения Фишера: 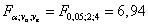. Так как фактическое отношение Фишера меньше критического, с вероятностью 95% принимаем гипотезу о том, что объём двигателя не влияет на потребление топлива. Однако, если мы выбираем уровень значимости α = 0,1, то фактическое значение отношения Фишера 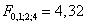и тогда с вероятностью 95% можем принять, что объём двигателя влияет на потребление топлива.

Фактическое отношение Фишера для фактора B 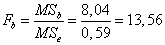, критическое значение отношения Фишера: 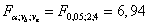. Так как фактическое отношение Фишера больше критического значения отношения Фишера, с вероятностью 95% принимаем, что вид топлива влияет на его потребление.

Пример 3.

Двухфакторный дисперсионный анализ без повторений можно провести с помощью процедуры MS Excel Двухфакторный дисперсионный анализ без повторений. Используем его для анализа данных о связи типа вида топлива и его потребления из примера 2.

В меню MS Excel выполняем команду Сервис/Анализ данных и выбираем средство анализа Двухфакторный дисперсионный анализ без повторений.

Заполняем данные также, как и в случае с однофакторным дисперсионным анализом.

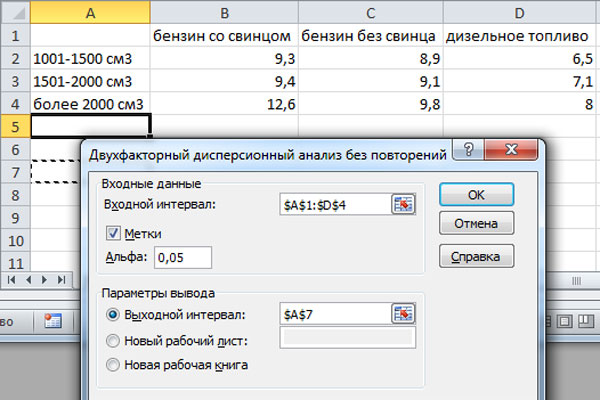
В результате действия процедуры выводятся две таблицы. Первая таблица - Итоги. В ней содержатся данные обо всех классах градации фактора: число наблюдений, суммарное значение, среднее значение и дисперсия.

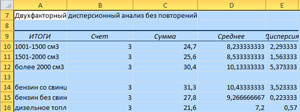
Во второй таблице - Дисперсионный анализ - содержатся данные об источниках вариации: рассеивании между строками, рассеивании между столбцами, рассеивании ошибки, общем рассеивании, сумма квадратов отклонений (SS), число степеней свободы (df), дисперсия (MS). В последних трёх столбцах - фактическое значение отношения Фишера(F), p-уровень (P-value) и критическое значение отношения Фишера (F crit).

Дисперсионный анализ
Источник вариации			SS		df
Строки			6,26		2
Столбцы			16,08667		2
Погрешность			2,373333		4
Итого			24,72		8
MS	F	P-value		F crit
3,13	5,275281

0,075572

6,94476

8,043333 13,55618

0,016529

6,944276

0,593333              

Фактор A (объём двигателя) сгруппирован в строках. Так как фактическое отношение Фишера 5,28 меньше критического 6,94, с вероятностью 95% принимаем, что потребление топлива не зависит от объёма двигателя.

Фактор B (вид топлива) сгруппирован в столбцах. Фактическое отношение Фишера 13,56 больше критического 6,94, поэтому с вероятностью 95% принимаем, что потребление топлива зависит от его вида.

Пример 4.

Торговое предприятие имеет три магазина - A, B и C. Проводятся две рекламные кампании. Требуется выяснить, зависят ли средние дневные доходы магазинов от двух рекламных кампаний. Для процедуры проверки случайно выбраны по 3 дня каждой рекламной кампании (то есть число повторений r = 3). Результаты обобщены в таблице:

Рекламная кампания	Магазин A	Магазин B	Магазин C
Рекламная кампания 1	12,05	15,17	9,48	14,53
	23,94	18,52	6,92
	14,63	19,57	10,47
Рекламная кампания 2	25,78	21,40	7,63	15,86
	17,52	13,59	11,90
	18,45	20,57	5,92
Среднее	18,73	18,14	8,72

Факторы, подлежащие проверке: магазин (A, B и C) и рекламная кампания (1 и 2). Пусть эти факторы не зависят друг от друга.

Вычислим суммы квадратов отклонений:

SS = 592,47

SS_a = 8,01,

SS_b = 378,38,

SS_ab = 13,85,

SS_e = 192,22.

Числа степеней свободы:

v_a = a − 1 = 2 − 1 = 1,

v_b = b − 1 = 3 − 1 = 2,

v_ab = (a − 1)(b − 1) = 2,

v_e = ab(r − 1) = 12,

v = abr − 1 = 17.

Дисперсии:

,

,

,

.

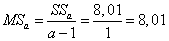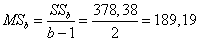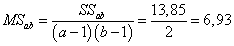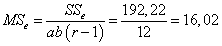Фактические отношения Фишера:

для фактора A: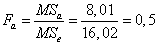

для фактора B: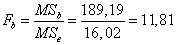

для взаимодействия факторов A и B: .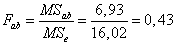

Критические значения отношения Фишера:

для фактора A: ,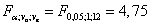

для фактора B: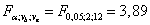

для взаимодействия факторов A и B: .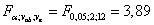

Делаем выводы:

о влиянии фактора A: фактическое отношение Фишера меньше критического значения, следовательно, рекламная кампания существенно не влияет на дневные доходы магазина с вероятностью 95%,

о влиянии фактора B: фактическое отношение Фишера больше критического, следовательно, доходы существенно различаются между магазинами,

о взаимодействии факторов A и B: фактическое отношение Фишера меньше критического, следовательно, взаимодействие рекламной кампании и конкретного магазина не существенно.

 

0,492897

4,747221

189,1904 11,81066

0,001462

3,88529

6,925272 0,432327

0,658717

3,88529

16,01861              

Для фактора A фактическое отношение Фишера меньше критического значения, следовательно, рекламная кампания существенно не влияет на дневные доходы магазина с вероятностью 95%.

Для фактора B фактическое отношение Фишера больше критического, следовательно, с вероятностью 95% доходы существенно различаются между магазинами.

Для взаимодействия факторов A и B фактическое отношение Фишера меньше критического, следовательно, с вероятностью 95% взаимодействие рекламной кампании и конкретного магазина не существенно.

ПРАКТИЧЕСКИЕ ЗАДАНИЯ

Однофакторный ДА

Задание 1.

В педагогическом эксперименте участвовали три группы студентов по 10 человек в каждой. В группах применили различные методы обучения: в первой – традиционный (F₁), во второй – основанный на компьютерных технологиях (F₂), в третьей – метод, широко использующий задания для самостоятельной работы (F₃). Знания оценивались по десятибалльной системе.

Требуется обработать полученные данные об экзаменах и сделать заключение о том, значимо ли влияние метода преподавания, приняв за уровень значимости α=0.05.
Результаты экзаменов заданы таблицей, F_j – уровень фактора x_ij – оценка i-го учащегося обучающегося по методике F_j.

 

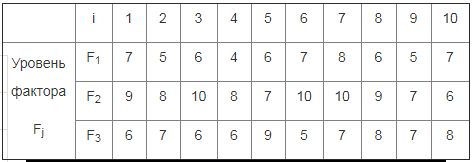
 Формулы для расчета

 

Расчетные данные свести в таблицу

Источник вариации	Сумма квадратов SS	Степени свободы df	Оценка дисперсии MS	Расчетное F	Критическое F кр
между группами
внутри групп
общая

 

Сделать выводы по проведенным исследованиям.

 

Задание 2.

Сведения о количестве голосов Y, отданных за кандидата в трех однотипных случайно выбранных избирательных округах, в которых использовались разные виды агитации (A(1) — личные встречи кандидата с избирателями, A(2) — раздача листовок с программой кандидата, A(3) — выступление кандидата по телевидению), приведены в таблице.

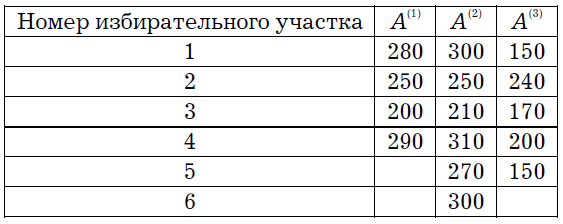
В однофакторном дисперсионном анализе проверяют гипотезу, состоящую в том, что эффекты влияния зафиксированных уровней фактора  A равны нулю — количество голосов, отданных за кандидата при каждом виде агитации, не зависит от вида агитации.

Задание 3.

Менеджер по продажам в сети супермаркетов хочет знать, влияет ли расположение рекламных щитов на объем продаж товара. Для каждого из трех видов щитов отобрано случайным образом по 6 магазинов, расположенных в соответствующем районе. Объемы продаж за месяц (млн. руб.) приведены в таблице. Решить задачу с использованием надстройки Excel.

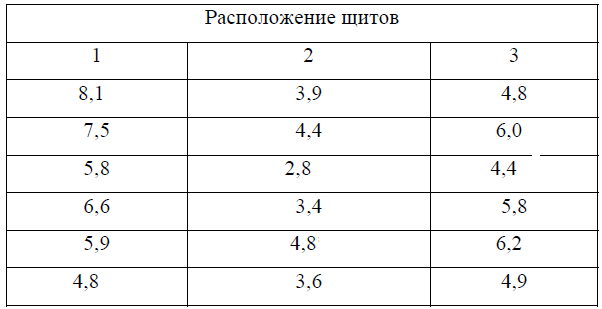
Задание 4.

Компания, производящая спортивные товары, желает сравнить расстояние, которое пролетают мячи, изготовленные по 4 разным технологиям. По каждой технологии произведено по 10 мячей. Мячи переданы для испытания в спортивный клуб, где испытаны в течение короткого промежутка времени при одинаковых погодных условиях. Результаты испытаний в м.:

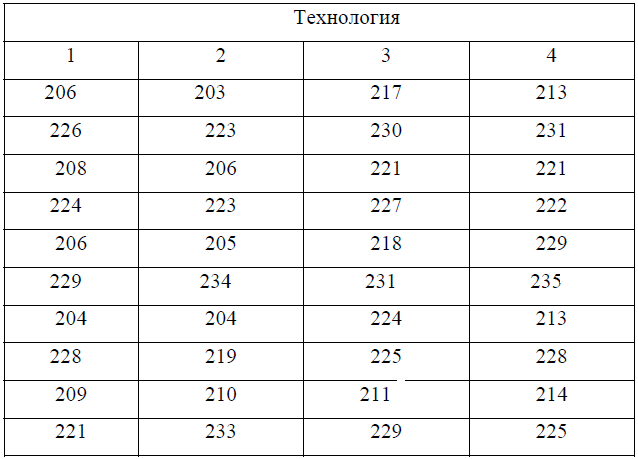
Решить задачу с использованием надстройки Excel.

Задание 5.

При исследовании зависимости средней оценки Y по математической статистике в группе от метода обучения (A(1) — традиционный классический, A(2) —компьютерный, A(3) — комбинированный), будущего направления подготовки (B(1) — «Менеджмент», B(2) — «Социология») и их взаимодействия было выделено случайным образом 18 групп, которые приписывались в равных количествах шести комбинациям методов и специальностей. Знания оценивались тестом, состоящим из 120 вопросов. Сведения о среднем числе правильных ответов в группах приведены в таблице.

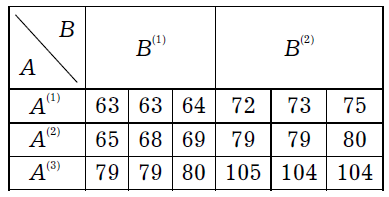
Задание 6.

Необходимо выяснить, различна ли в среднем урожайность разных сортов картофеля независимо от применяемого удобрения и различна ли эффективность используемых удобрений независимо от сорта.

	Сорт 1	Сорт 2	Сорт 3	Сорт 4	Сорт 5
1 участок	6	9	6	2	6
2 участок	4	7	8	3	5
3 участок	9	3	10	7	4
4 участок	8	4	14	4	10
5 участок	15	11	13	9	14
6 участок	12	14	15	11	9

 Решить задачу с использованием надстройки Excel.

Задание 7.

Проверка влияния возраста и стажа работников определенной специальности на производительность труда. Это результаты обследования 60 работников производства, у которых фиксировалась средняя часовая выработка в натуральных единицах продукции.

 

Стаж

Возраст

от 25 до 35 от 35 до 45 от 45 до 55 от 1 до 4 лет 19 19 18 20 20 19 20 20 20 20 23 21 22 25 23 от 4 до 7 лет 30 20 19   31 29 25   32 30 25   32 31 26   34 31 26 от 7 до 10 лет 35 36 24   35 40 24   39 41 24   40 42 25   41 45 25 Свыше 10 лет 40 28 20   40 31 24   41 35 25   41 36 31   42 40 32

Решить задачу с использованием надстройки Excel.

Задание 8.

При выращивании помидоров на тридцати участках применялись пять видов удобрений и шесть технологий выращивания. Каждый участок был разбит на четыре делянки, т.е. каждой паре уровней факторов (вид удобрений, технология выращивания) соответствуют четыре значения показателя урожайности (табл.). Влияют ли факторы (вид удобрений и технология выращивания) на урожайность продукции?

	Техн. 1	Техн. 2	Техн. 3	Техн. 4	Техн. 5	Техн. 6
Вид А	133	142	134	140	140	144
	147	133	148	132	146	145
	137	141	127	142	136	144
	128	124	138	134	131	134
Вид Б	127	137	120	127	127	127
	130	123	128	126	122	138
	131	131	146	125	144	126
	132	141	144	124	122	122
Вид В	121	122	149	127	120	127
	128	145	131	127	129	125
	137	145	144	142	146	139
	128	131	125	141	125	148
Вид Г	131	137	123	127	123	124
	123	138	144	146	135	125
	139	136	122	122	142	139
	137	127	131	120	129	125
Вид Д	149	148	132	143	131	127
	136	141	120	128	142	135
	129	149	125	135	131	145
	135	129	146	126	130	133

 

Решить задачу с использованием надстройки Excel.

Занятие 5.

 ДИСПЕРСИОННЫЙ АНАЛИЗ

1. Однофакторный дисперсионный анализ. 1

Пример 1. 3

2 Двухфакторный дисперсионный анализ. 4

Пример  2. 5

3 Двухфакторный дисперсионный анализ без повторений в MS Excel. 6

Пример 3. 6

4 Двухфакторный дисперсионный анализ с повторениями.. 8

Пример 4. 10

5 Двухфакторный дисперсионный анализ с повторениями в MS Excel. 12

6 Практические задания. 13

6.1 Однофакторный ДА.. 13

Задание 1. 14

Задание 2. 14

Задание 3. 14

Задание 4. 15

6.2 Двухфакторный дисперсионный анализ без повторений. 15

Задание 5. 15

Задание 6. 15

6.3 Двухфакторный дисперсионный анализ с повторением.. 16

Задание 7. 16

Задание 8. 16

ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

 

Дисперсионный анализ предназначен для исследования задачи о действии на измеряемую случайную величину (отклик) одного или нескольких независимых факторов, имеющих несколько градаций. В однофакторном, двухфакторном и т. д. анализе влияющие на результат факторы считаются известными, и речь идет только о выяснении существенности или оценке этого влияния.

Применение дисперсионного анализа возможно, если можно предполагать соответствие выборочных групп генеральным совокупностям с нормальным распределением и независимость распределений наблюдений в группах.

Задача заключается в том, чтобы сравнить дисперсию, обусловленную случайными причинами, с дисперсией вызываемой наличием исследуемого фактора. Если они значимо различаются, то считают, что фактор оказывает статистически значимое влияние на исследуемую переменную. Значимость различий проверяется по критерию Фишера.

Влияние случайной составляющей характеризуют внутри- групповая дисперсия, а влияние изучаемого фактора—межгрупповая. Внутригрупповая дисперсия рассчитывается по формуле:

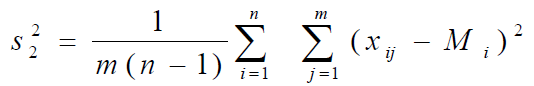
межгрупповая:

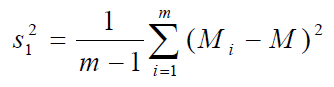
Здесь M — общее среднее,   т — количество групп,  п — количество элементов в группе.

В MS Excel для проведения однофакторного дисперсионного анализа используется процедура Однофакторный дисперсионный анализ. Для проведения дисперсионного анализа необходимо:

- ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соответствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора;

- выполнить команду Сервис > Анализ данных;

- в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;

- в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши

- в разделе Группировка переключатель установить в положение по столбцам;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;

- нажать кнопку ОК.

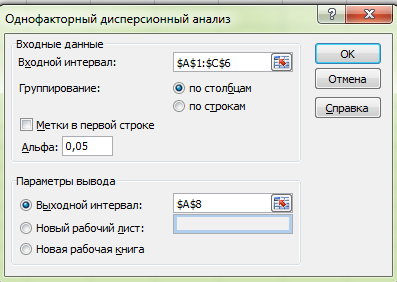
Пример заполнения диалогового окна Однофакторный дисперсионный анализ

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа: средние, дисперсии, критерий Фишера и другие показатели.

Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение. В случаях, когда Р-Значение < 0,05, критерий Фишера значим и влияние исследуемого фактора можно считать доказанным.

Кроме рассмотренной процедуры однофакторного дисперсионного анализа, для проведения двухфакторного дисперсионного анализа в пакете анализа реализованы процедуры Двухфакторный дисперсионный анализ с повторениями и Двухфакторный дисперсионный анализ без повторений.

Пример 1.

Необходимо выявить, влияет ли расстояние от центра города на степень заполняемости гостиниц. Пусть введены 3 уровня расстояний от центра города: 1) до 3 км, 2) от 3 до 5 км и 3) свыше 5 км. Данные заполняемости представлены в таблице.

Решение.

1. Исследуемые данные введите в рабочую таблицу Excel по столбцам: в столбец А — заполняемость гостиниц в центре города, в столбец  В— гостиниц, находящихся на расстоянии от 3 до 5 км и т. д. (диапазон А1:С6).

2. Выполните команду Сервис > Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа щелчком мыши выберите процедуру Однофакторный дисперсионный анализ. Нажмите кнопку ОК.

3. В появившемся диалоговом окне Однофакторный дисперсионный анализ в поле Входной интервал задайте А 1: С 6. Для этого наведите указатель мыши на ячейку А1 и протяните его к ячейке С6 при нажатой левой кнопке мыши.

4. В разделе Группировка переключатель установите в положение по столбцам.

5. Далее необходимо указать выходной диапазон. Для этого поставьте переключатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем щелкните указателем мыши в правом поле ввода Выходной интервал, и щелчком мыши на ячейке А8 укажите расположение выходного диапазона. Нажмите кнопку ОК.

Результаты анализа. В результате будет получена таблица

Результат работы инструмента Однофакторный дисперсионный анализ

 

Интерпретация результатов.

В таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение находится величина 0,0002684. Величина Р-Значение < 0,05, следовательно, критерий Фишера значим и влияние фактора расстояния от центра города на эффективность заполнения гостиниц доказано статистически.