Двухфакторный дисперсионный анализ применяется для того, чтобы проверить возможную зависимость результативного признака от двух факторов - A и B. Тогда a- число градаций фактора A и b - число градаций фактора B. В статистическом комплексе сумма квадратов остатков разделяется на три компоненты:

SS = SS_a + SS_b + SS_e,

где

SS - общая сумма квадратов отклонений

SS _а - объяснённая влиянием фактора A сумма квадратов отклонений

SS_b - объяснённая влиянием фактора B сумма квадратов отклонений

SS_e -  сумма квадратов отклонений ошибки

MS _а - дисперсия, объяснённая влиянием фактора A

MS_b - дисперсия, объяснённая влиянием фактора B

MS_e -  необъяснённая дисперсия или дисперсия ошибки

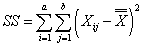
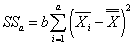
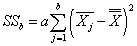
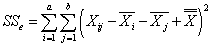
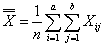
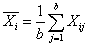
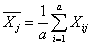
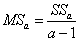
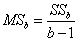
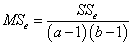
где

v_a = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,

v_b = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,

v_e = (a − 1)(b − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,

v = ab − 1 - общее число степеней свободы.

Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:

Чтобы определить влияние фактора A, нужно фактическое отношение Фишера

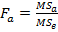сравнить с критическим отношением Фишера .

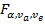Чтобы определить влияние фактора B, нужно фактическое отношение Фишера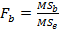

сравнить с критическим отношением Фишера .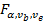

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.

Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.

Пример  2.

Дана информация о среднем потреблении топлива на 100 километров в литрах в зависимости от объёма двигателя и вида топлива.

	Бензин со свинцом	Бензин без свинца	Дизельное топливо	Среднее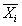
1001-1500 см³	9,3	8,9	6,5	8,23
1501-2000 см³	9,4	9,1	7,1	8,53
Более 2000 см³	12,6	9,8	8,0	10,13
Среднее	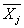10,42	9,27	7,2

Требуется проверить, зависит ли потребление топлива от объёма двигателя и вида топлива.

Решение.

Для фактора A число классов градации a = 3, для фактора B число классов градации b = 3.

Вычисляем суммы квадратов отклонений:

,

,

,

.

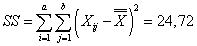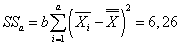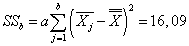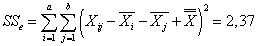Соответствующие дисперсии:

,

,

.

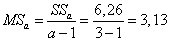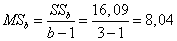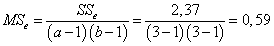Фактическое отношение Фишера для фактора A 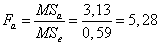, критическое значение отношения Фишера: 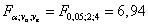. Так как фактическое отношение Фишера меньше критического, с вероятностью 95% принимаем гипотезу о том, что объём двигателя не влияет на потребление топлива. Однако, если мы выбираем уровень значимости α = 0,1, то фактическое значение отношения Фишера 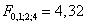и тогда с вероятностью 95% можем принять, что объём двигателя влияет на потребление топлива.

Фактическое отношение Фишера для фактора B 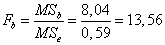, критическое значение отношения Фишера: 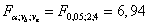. Так как фактическое отношение Фишера больше критического значения отношения Фишера, с вероятностью 95% принимаем, что вид топлива влияет на его потребление.