Результатов измерений
2.1 Цель работы: приобретение практических навыков выполне-
ния измерения физических величин и обработка результатов измерений.
2.2 Характер выполнения работы: каждый студент выполняет работу индивидуально.
2.3 Теоретическая часть
Измерение – это определение значения физической величины опытным путём с помощью специально предназначенных для этого технических средств. При измерениях получают количественную информацию об измеряемой величине. По способу получения числового значения измеряемой величины все измерения делят на прямые, косвенные, совокупные, совместные.
Совокупность приёмов использования, принципов и средств измерений называют методом измерений. Важнейшими являются следующие методы измерений: непосредственной оценки, сравнение с мерой, противопоставление, замещения, нулевой, дифференциальный, перестановки, дополнения, совпадений.
Для измерения физических величин используют технические средства. Технические средства, которые используют при измерениях и имеют нормированные метрологические характеристики, называют средствами измерений.
Все средства измерений подразделяют на меры, измерительные преобразователи, измерительные приборы, измерительные установки и системы.
К метрологическим характеристикам средств измерений относят: вид шкалы, цена деления, класс точности прибора.
Шкалы приборов характеризуются такими показателями: предел измерения по шкале прибора, цена деления шкалы.
Под классом точности средств измерения (ГОСТ 16263-70) понимается такая обобщённая характеристика, которая определяется пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность измерений.
Обозначение класса точности прибора наносится на циферблаты, щитки и корпуса средств измерений, приводятся в нормативных документах и могут быть представлены в различном виде.
Средствам измерений (ГОСТ 13600-80), пределы допускаемых погрешностей которых выражаются в виде приведённых погрешностей, должны присваиваться классы точности, выбираемые из ряда чисел (1; 1,5; 1,6; 2,5; 3; 4; 5; 6) х 10п, где п = 1, 0,-1, -2 и т.д. Это означает, что значение измеряемой величины не отличается от того, что показывает указатель отсчётного устройства, более, чем на соответствующее число процентов от верхнего предела измерений.
Обозначения могут иметь форму заглавных букв латинского алфавита (например, М, С и т.д.) или римских цифр (I, II, III, IV и т.д.) с добавлением условных знаков, обозначаться в виде дроби (0,02/0,01). Смысл таких обозначений раскрывается в нормативной документации. Существуют и другие обозначения классов точности средств измерений.
Класс точности является обобщённой характеристикой средств измерений. Знание его позволяет определить не точность конкретного измерения, а лишь указать пределы, в которых находится значение измеряемой величины. Ошибки измерений могут возникать по многим причинам.
Однако даже при соблюдении всех условий достаточно точно измерить значение физической величины при однократном измерении сложно, поэтому проводят многократные измерения физической величины.
При проведении в одинаковых условиях повторных измерений одной и той же величины получаются результаты наблюдений, которые в ряде случаев отличаются друг от друга, а в ряде совпадают. Такие расхождения в результате измерения говорят о наличии в них случайных погрешностей, а также присутствии промахов (грубых погрешностей). Целью обработки результатов измерений является установление значения измеряемой величины и погрешности полученного результата. Для получения оценки измеряемой величины максимально близкой к истинному значению необходимо по экспериментальным данным, выявить и исключить промахи, найти оценку математического ожидания отдельных результатов наблюдений, оценить систематическую погрешность и исключить её из оценки математического ожидания. Точность оценки математического ожидания ряда наблюдений зависит от количества выполненных измерений и от дисперсии случайной составляющей погрешности. Поэтому по экспериментальным данным приходится оценивать не только математическое ожидание, но и дисперсию.
2.4 Материальное обеспечение
Фотоэлектроколориметр К-77, стаканы химические (на 100мл), растворы для колориметрирования, бумага фильтровальная.
2.5 Порядок выполнения работы
Работу выполняют в следующем порядке:
- определение вида и метода измерений, типа средств измерений;
- определение класса точности прибора, погрешности измерений;
- ознакомление с устройством прибора и порядком работы на нём;
- выполнение многократных измерений значений физической величины;
- обработка полученных экспериментальных данных и оценка погрешности измерения;
- оформление отчёта.
2.4.1 Измерения выполняют на фотоэлектрическом колориметре
К-77.
Фотоэлектрический колориметр предназначен для определения концентрации цветных веществ или веществ, вступающих в цветные реакции путём сравнения с эталоном известной концентрации.
Подготовка прибора к измерениям
Перед выполнением колориметрических измерений необходимо предварительно выполнить следующие операции:
- проверить, находится ли стрелка измерителя в нулевом положении, если нет, необходимо её привести в нулевое положение вращением нуль-корректора (позиция 3);
- установить в гнездо соответствующий монохроматизирующий фильтр (позиция 7);
- включить прибор в питающую сеть путём нажатия клавиши (позиция 4);
- установить в бакелитовый блок под крышкой (позиция 8) корзинку (позиция 6) с двумя кюветами, заполненными дистиллированной водой, опустить крышку, установить корзинку в одно из крайних положений, установить с помощью рукоятки (позиция 2) стрелку измерителя в положение около 100оТ . Мелкие отклонения исправить рукояткой прецизера (позиция 1);
- подождать несколько минут для стабилизации температуры прибора. По мере необходимости повторно выполнить коррекцию положения стрелки измерителя на 100оТ;
- установить корзинку в центральном положении. Проверить находится ли стрелка измерителя в нулевом положении (в случае заметного отклонения стрелки от нулевого положения, регулировкой нуля (позиция 5) установить стрелку измерителя в нулевое положение);
- переместить корзинку в противоположное крайнее положение и проверить показания измерителя. Если измеряемые кюветы равносильны в спектральном отношении, тогда разность показаний не должна превышать 1 деления шкалы Т.
Внешний вид прибора представлен на рисунке1.
4 5 6 7 8
3
2
1
F
1– точная регулировка чувствительности;
2– грубая регулировка чувствительности;
3– нуль-корректор;
4– сетевой выключатель;
5– регулировка нуля;
6– корзинка;
7- патрон фильтров;
8– крышка.
Рисунок 1 – Фотоэлектрический колориметр
Измерения
Порядок измерений заключается в следующем:
- заполнить одну кювету эталонным раствором (дистиллированной водой), вторую раствором сравнения. Установит нужный светофильтр. Светофильтр по цвету исследуемого раствора может быть выбран по таблице 3.
Таблица 3 – Выбор светофильтра по цвету исследуемого раствора
| Характеристика исследуемого вещества | Цвет светофильтра | Длина волны пропускаемого света, нм | |
| окраска раствора | длина волны, нм | ||
| жёлтая красная фиолетовая синяя сине-зелёная | 425 490 530 590 640 | синий зелёный зелёно-жёлтый оранжевый красный | 400…430 460…500 520…550 590 600…650 |
- установить корзинку с кюветами в крайнее положение таким образом, чтобы пучок света проходил через кювету со сравниваемым раствором (дистиллированной водой) и установить стрелку измерителя в положение 100оТ;
- переместить корзинку с кюветами в противоположное крайнее положение так, чтобы пучок света проходил через кювету с эталонным раствором (исследуемый) и отметить на измерителе значение (светопоглащение).
2.4.2 Обработка результатов с многократными измерениями
При проведении данной практической работы можно определить различные многократные измерения физической величины, использовав при этом разнообразные средства измерений.
Математическую обработку результатов эксперимента проводят по всем данным, полученными студентами.
Полученные данные обрабатывают в следующей последовательности:
1. Исключают грубые погрешности (промахи).
Для этого располагают все измерения в порядке возрастания и определяют «выскакивающие» величины, наибольшие или наименьшие. Если величина имеет наибольшее крайнее значение, то составляют по
Q =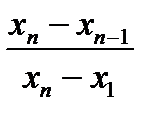 
(1)
где числитель – разность между предполагаемыми крайним
«выскакивающим» значением и значением,
которое ему предшествует;
знаменатель – разность между наибольшим и наименьшим
значением измерений.
Вычисленную величину «Q» оценивают с помощью табличного значения, которое выбирают в соответствии с выбранным значением уровня значимости числа измерений «n».
Наличие «выскакивающего» значения будет доказано, если «Q» вычисленное будет больше, чем табличное значение «Q» (таблица 4)
Также можно провести и предположение о том, что «выскакивающей» величиной являются крайнее наименьшее значение. Рассчитывают аналогичное вышеописанному отношение
Q =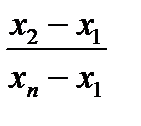 
, (2)
и сравнивают с табличным значением.
Таблица 4 – Значение критерия «Q» для определения грубых ошибок
| Число измерений | q = 0,05 | q = 0,01 |
| 3 4 5 6 7 8 9 10 11 12 15 20 | 0,941 0,765 0,642 0,560 0,507 0,468 0,437 0,412 0,392 0,376 0,338 0,300 | 0,988 0,889 0,780 0,698 0,637 0,590 0,555 0,527 0,502 0,482 0,438 0,391 |
2. Определяют среднее арифметическое значение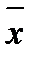 
результатов наблюдений хi
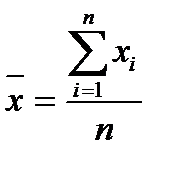, (3)
где хi - значение параметра в отдельном опыте;
n – число изменений.
3. Определяют отклонение для среднего значения для каждого результата (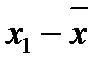 
) и полученное отклонение возводят в квадрат. Полученные результаты заносят в таблицу 5.
Таблица 5 – Определение суммы квадрата отклонения
| Число измерений | Результаты отдельных измерений | Отклонения от среднего арифметического | Квадрат отклонения |
| 
| 
| |
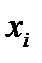
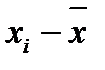
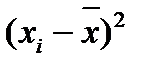
| 1 2 3 и т.д. |
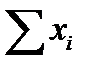
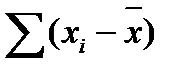
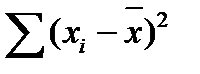
4. Вычисляют экспериментальную оценку дисперсии воспроизводимости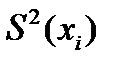 
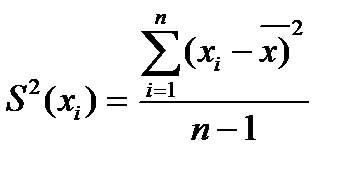, (4)
5. Вычисляют экспериментальную оценку стандартного отклонения отдельного определения S (xi)
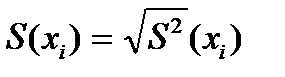, (5)
6. Вычисляют экспериментальную оценку стандартного отклонения среднего результата 
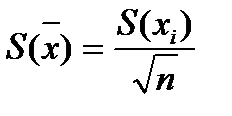, (6)
7. Получают надёжность полученных результатов по критерию Стьюдента t α при избранной доверительной вероятности α (0,95 или 0,99). Критерий Стьюдента находят по таблице 6, в зависимости от уровня значимости q, который при заданной вероятности равен 0,05 или 0,01 соответственно, и числа степеней свободы f, которое зависит от количества опытов n
f = n – 1, (7)
Таблица 6 – Значение критерия Стьюдента при различных уровнях
значимости
| Число степеней свободы, f | Уровень значимости, q | |
| при 0,05 | при 0,01 | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 30 | 12,71 4,30 3,18 2,78 2,57 2,45 2,37 2,31 2,26 2,23 2,20 2,18 2,16 2,15 2,04 | 63,66 9.93 5,84 4,60 4,03 3,71 3,50 3.36 3,25 3,17 3,11 3,06 2,01 2,98 2,75 |
Найдя tα, зная стандартное отклонение среднего результата, рассчитывают ошибку полученного среднего результата ξα
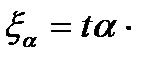s 
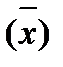, (8)
8. Устанавливают интервал, в котором с выбранной доверительной вероятностью α находится средний результат
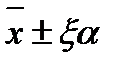, (9)
9. Определяют относительную ошибку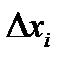 
, %
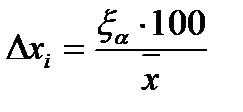, (10)
Если относительная ошибка оказывается больше 10 %, это указывает на то, что грубые ошибки полностью не были исключены. Тогда выявляют вновь грубые ошибки и производят повторную обработку экспериментальных данных.
2.5.3 Оформление отчёта
При оформлении отчёта указывается название, цель работы, вид и метод измерения. Производится рисунок шкалы прибора и его характеристика: предел, цена деления, класс точности.
Приводятся полученные экспериментальные данные и математическая обработка результатов исследования.
2.6 Контрольные вопросы
1. Что такое измерение?
2. Классификация измерений по видам и методам.
3. Приведите классификацию средств измерений.
4. Что называется метрологическими характеристиками средств измерений?
5. Что понимается под классом точности средств измерений?
6. Как обозначается класс точности измерительных приборов?
7. Приведите последовательность обработки экспериментальных данных.
8. Что такое «промахи» и грубые погрешности?
9. Каков порядок исключения грубых погрешностей?
10. Что такое систематическая погрешность?
11. Как можно исключить систематические погрешности (до начала измерения, в процессе измерения)?
12. Какие методы измерений применяют при оценке качества сырья, полуфабрикатов и готовой продукции?
13. Какая доверительная вероятность считается достаточно надёжной при проведении физико-химических исследований?
Практическая работа № 3
Дата: 2019-02-25, просмотров: 245.
