· Распределение Ферми по энергиям для свободных электронов в металле:
при 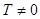
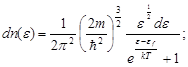
при 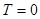
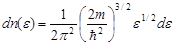 (при
(при 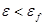 ),
),
где 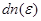 - концентрация электронов, энергия которых заключена в интервале значений от
- концентрация электронов, энергия которых заключена в интервале значений от 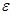 до
до 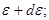 m и
m и 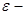 - масса и энергия электрона;
- масса и энергия электрона; 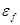 - уровень ( или энергия ) Ферми.
- уровень ( или энергия ) Ферми.
· Уровень Ферми в металле при T = 0
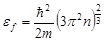 .
.
· Температура 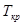 вырождения
вырождения
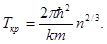
· Удельная проводимость собственных полупроводников
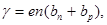
где e - заряд электрона; n - концентрация носителей заряда (электронов и дырок); 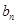 и
и 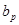 -подвижности электронов и дырок.
-подвижности электронов и дырок.
Напряжение UН на гранях образца при эффекте Холла
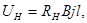
где RН - постоянная Холла; B - индукция магнитного поля; 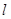 - ширина пластины; j - плотность тока.
- ширина пластины; j - плотность тока.
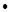 Постоянная Холла для полупроводников типа алмаза, кремния, германия и др., обладающих носителями заряда одного вида (n или p),
Постоянная Холла для полупроводников типа алмаза, кремния, германия и др., обладающих носителями заряда одного вида (n или p),
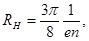
где 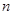 - концентрация носителей заряда.
- концентрация носителей заряда.
Примеры решения задач
Пример 1. Материальная точка массой т = 5 г совершает гармонические колебания с частотой v = 0,5 Гц. Амплитуда колебаний А = 3 см. Определить: 1) скорость u точки в момент времени, когда смещение х = 1,5 см; 2) максимальную силу .Fmax действующую на точку; 3) полную энергию Е колеблющейся точки.
Решение. 1. Уравнение гармонического колебания имеет вид

а формулу скорости получим, взяв первую производную по времени от смещения:
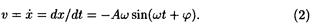
Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на А2, второе на А2w2 и сложим:
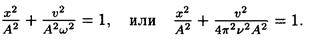
Решив последнее уравнение относительно υ, найдем
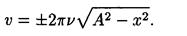
Выполнив вычисления по этой формуле, получим
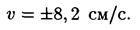
Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус, — когда направление скорости совпадает с отрицательным направлением оси х.
Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением
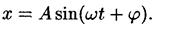
Повторив с этим уравнением такое же решение, получим тот же ответ.
2. Силу, действующую на точку, найдем по второму закону Ньютона:

где а — ускорение точки, которое получим, взяв производную по времени от скорости:
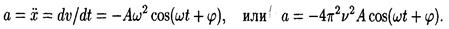
Подставив выражение ускорения в формулу (3), получим
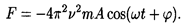
Отсюда максимальное значение силы
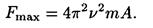
Подставив в это уравнение значения величин p, υ, т и A, найдем
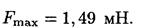
3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени.
Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия Е колеблющейся точки равна максимальной кинетической энергии
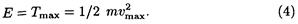
Максимальную скорость определим из формулы (2), положив cos ( wt + j ) = 1: umax = 2 p vA . Подставив выражение скорости в формулу (4), найдем
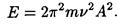
Подставив значения величин в эту формулу и произведя вычисления, получим
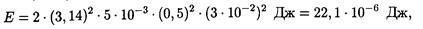
или Е = 22,1 мкДж.
Пример 2. Физический маятник представляет собой стержень длиной l = 1 м и массой 3 m 1 с прикрепленным к одному из его концов обручем диаметром d = 1/2l и массой m1. Горизонтальная ось Оz маятника проходит через середину стержня перпендикулярно ему. Определить период Т колебаний такого маятника.
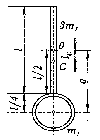 Решение. Период колебаний физического маятника определяется по формуле
Решение. Период колебаний физического маятника определяется по формуле
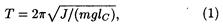
где J — момент инерции маятника относительно оси колебаний; т — его масса; lc — расстояние от центра масс маятника до оси колебаний.
Момент инерции маятника равен сумме моментов инерции стержня J1 и обруча J 2:

Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определяется по формуле J1 = 1/12 ml 2 . В данном случае т = 3m1 и
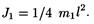
Момент инерции обруча найдем, воспользовавшись тео-ремой Штейнера J = J 0 + mа2, где J — момент инерции относительно произвольной оси; J0 — момент инерции относительно оси, проходящей через центр масс параллельно заданной оси; а — расстояние между указанными осями. Применив эту формулу к обручу, получим
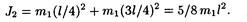
Подставив выражения J 1 и J2 в формулу (2), найдем момент инерции маятника относительно оси вращения:
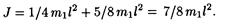
Расстояние l с от оси маятника до его центра масс равно
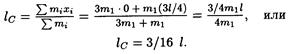
Подставив в формулу (1) выражения J , l с и массы маятника (т = 3 m 1 + m 1 = 4 m 1), найдем период его колебаний:
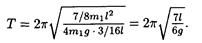
После вычисления по этой формуле получим
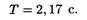
Пример 3. Поперечная волна распространяется вдоль упругого шнура со скоростью u = 15 м/с. Период Т колебаний точек шнура равен 1,2 с, амплитуда А = 2 см. Определить: 1) длину волны А; 2) фазу j колебаний, смещение ξ, скорость 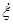 и ускорение
и ускорение 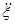 точки, отстоящей на расстоянии х = 45 м от источника волн в момент t = 4 с; 3) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х1 = 20 м и x2 = 30 м.
точки, отстоящей на расстоянии х = 45 м от источника волн в момент t = 4 с; 3) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х1 = 20 м и x2 = 30 м.
Решение. 1. Длина волны равна расстоянию, которое волна проходит за один период, и может быть найдена из соотношения
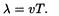
Подставив значения величин u и T, получим
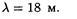
2. Запишем уравнение волны:

где ξ — смещение колеблющейся точки; х — расстояние точки от источника волн; u — скорость распространения волн.
Фаза колебаний точки с координатой х в момент времени t определяется выражением, стоящим в уравнении волны под знаком косинуса:
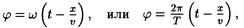
где учтено, что w == 2p/Т.
Произведя вычисления по последней формуле, получим
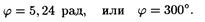
Смещение точки определим, подставив в уравнение (1) значения амплитуды А и фазы j:
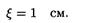
Скорость точки находим, взяв первую производную от смещения по времени:
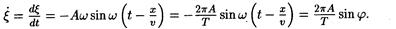
Подставив значения величин тp, А, Т и j и произведя вычисления, получим
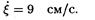
Ускорение есть первая производная от скорости по времени, поэтому
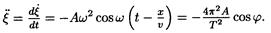
Произведя вычисления по этой формуле, найдем
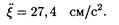
3. Разность фаз Dj колебаний двух точек волны связана с расстоянием Dx; между этими точками соотношением
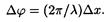
Подставив значения величин l, х1 и х2, и вычислив, получим
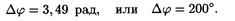
Пример 4. На расстоянии l = 4 м от источника плоской волны частотой v = 440 Гц перпендикулярно ее лучу расположена стена. Определить расстояния от источника волн до точек, в которых будут первые три узла и три пучности стоячей волны, возникшей в результате сложения бегущей и отраженной от стены волн. Скорость u волны считать равной 440 м/с.
Решение. Выберем систему координат так, чтобы ось х была направлена вдоль луча бегущей волны и начало О координат совпадало с точкой, находящейся на источнике MN плоской волны. С учетом этого уравнение бегущей волны запишется в виде

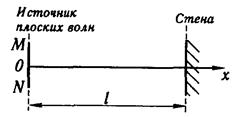
Поскольку в точку с координатой х волна возвратится, пройдя дважды расстояние l - х, и при отражении от стены, как среды более плотной, изменит фазу на p, то уравнение отраженной волны может быть записано в виде
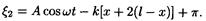
После очевидных упрощений получим
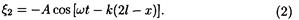
Сложив уравнения (1) и (2), найдем уравнение стоячей волны:
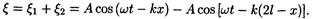
Воспользовавшись формулой разности косинусов, найдем
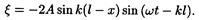
Так как выражение Asink ( l - x ) не зависит от времени, то, взятое по модулю, оно может рассматриваться как амплитуда стоячей волны:
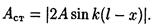
Зная выражение амплитуды, можем найти координаты узлов и пучностей.
Узлы возникнут в тех точках, где амплитуда стоячей волны равна нулю: |2Asink ( l - х)| = 0. Это равенство выполняется для точек, координаты xn которых удовлетворяют условию
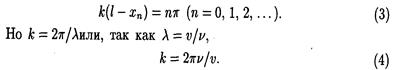
Подставив это выражение k в (3), получим
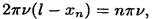
откуда координаты узлов
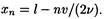
Подставив сюда значения l, u , v и п = 0,1,2, найдем координаты первых трех узлов:
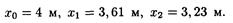
Пучности возникнут в тех точках, где амплитуда стоячей волны максимальна: 2Asin k (l - x ’ )=2A. Это равенство выполняется для точек, координаты x ' n которых удовлетворяют условию k ( l - x ' n )= (2n - 1)(p/2) (n = 0,1,2,3,...). Выразив здесь k по (4), получим
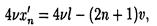
откуда координаты пучностей
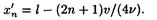
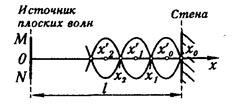
Подставив сюда значения l , u , v и п = 0,1,2, найдем координаты первых трех пучностей:
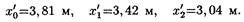
Границы максимальных смещений точек среды в зависимости от их координат изображены на рис.. Здесь же отмечены координаты x 1 , x2, x3 ... узлов и координаты 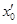 ,
, 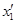 ,
, 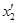 ,….. пучностей стоячей волны.
,….. пучностей стоячей волны.
Пример 5. На толстую стеклянную пластинку, покрытую очень тонкой пленкой, показатель преломления газ вещества которой равен 1,4, падает нормально параллельный пучок монохроматического света (l = 0,6 мкм). Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину d пленки.
Решение. Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения e1 ¹ 0, показан на рис. В точках A и В падающий пучок частично отражается и частично преломляется.
Отраженные пучки света AS 1 и BCS2 падают на собирающую линзу L , пересекаются в ее фокусе F и интерферируют между собой.
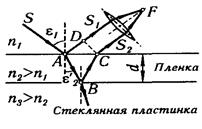
Так как показатель преломления воздуха (n1 = 1,00029) меньше показателя преломления вещества пленки (п2 = 1,4), который, в свою очередь, меньше показателя преломления стекла (n3 = 1,5), то в обоих случаях отражение происходит от среды оптически более плотной, чем та среда, в которой идет падающая волна. Поэтому фаза колебания пучка света AS 1 при отражении в точке А изменяется на p рад и точно так же на p рад изменяется фаза колебаний пучка света BCS 2 при отражении в точке В. Следовательно, результат интерференции этих пучков света при пересечении в фокусе F линзы будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого пучка не было.
Как известно, условие максимального ослабления света при интерференции в тонких пленках состоит в том, что оптическая разность хода D интерферирующих волн должна быть равна нечетному числу полуволн: D = (2 k +1)(l/2).
Как видно из рис., оптическая разность хода
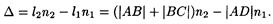
Следовательно, условие минимума интенсивность света примет вид
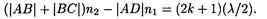
Если угол падения e1 будет уменьшаться, стремясь к нулю, то AD ® 0 и |АВ| + |ВС| ® 2d , где d — толщина пленки. В пределе при e1 = 0 будем иметь
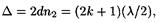
откуда искомая толщина пленки
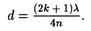
Полагая k = 0,1,2,3,..., получим ряд возможных значений толщины пленки:
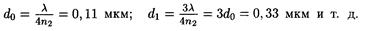
Пример 6. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны l = 0,6 мкм. В возникшей при этом интерференционной картине на отрезке длиной l = 1 см наблюдается 10 полос. Определить преломляющий угол q клина.
Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти пучки когерентны, и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные пучки света 1 и 2 будут практически параллельны.
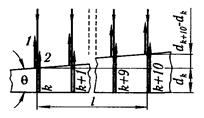
Темные полосы видны на тех участках клина, для которых разность хода кратна нечетному числу половины длины волны:
D = (2 k + 1) . ( l /2) , где k = 0, 1, 2, 3,… (1)
Разность хода D двух волн складывается из разности оптических длин путей этих волн (2dncos 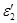 ) и половины длины волны (l/2). Величина l/2 представляет собой добавочную разность хода, возникающую при отражении волны от оптически более плотной среды. Подставляя в формулу (1) значение разности хода D, получим
) и половины длины волны (l/2). Величина l/2 представляет собой добавочную разность хода, возникающую при отражении волны от оптически более плотной среды. Подставляя в формулу (1) значение разности хода D, получим
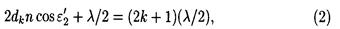
где п — коэффициент преломления стекла (п = 1,5); dk — толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; 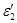 — угол преломления.
— угол преломления.
Согласно условию, угол падения равен нулю, следовательно, и угол преломления 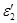 равен нулю, a cos
равен нулю, a cos 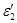 = 1. Раскрыв скобки в правой части равенства (2), после упрощения получим
= 1. Раскрыв скобки в правой части равенства (2), после упрощения получим

Пусть произвольной темной полосе номера k соответствует определенная толщина клина в этом месте dk, а темной полосе номера k +10 соответствует толщина клина dk+10. Согласно условию задачи, 10 полос укладываются на отрезке длиной l = 1 см. Тогда искомый угол будет равен

где из-за малости преломляющего угла sinq » q (угол q выражен в радианах).
Вычислив dk и dk+10 из формулы (3), подставив их в формулу (4) и произведя преобразования, найдем
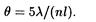
После вычисления получим
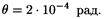
Выразим q в градусах. Для этого воспользуемся соотношением между радианом и секундой: 1 рад = 2,06" × 105, т. е.
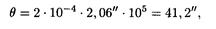
или в соответствии с общим правилом перевода из радиан в градусы
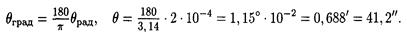
Искомый угол равен 41,2".
Пример 7. На диафрагму с круглым отверстием радиусом r = 1 мм падает нормально параллельный пучок света длиной волны l = 0,05 мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние bmах от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
Решение. Расстояние, при котором будет видно темное пятно, определяется числом зон Френеля, укладывающихся в отверстии. Если число зон четное, то в центре дифракционной картины будет темное пятно.
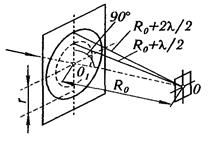
Число зон Френеля, помещающихся в отверстии, убывает по мере удаления экрана от отверстия. Наименьшее четное число зон равно двум. Следовательно, максимальное расстояние, при котором еще будет наблюдаться темное пятно в центре экрана, определяется условием, согласно которому в отверстии должны поместиться две зоны Френеля.
Из рисунка следует, что расстояние от точки наблюдения О на экране до края отверстия на 2 (l/2) больше, чем расстояние R0 = bmах.
По теореме Пифагора получим
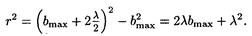
Учтя, что l < bmах и что членом, содержащим l2, можно пренебречь, последнее равенство перепишем в виде
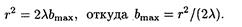
Произведя вычисления по последней формуле, найдем
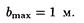
Пример 8. На дифракционную решетку нормально к ее поверхности падает параллельный пучок света с длиной волны l = 0,5 мкм. Помещенная вблизи решетки линза проецирует дифракционную картину на плоский экран, удаленный от линзы на L = 1 м. Расстояние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см . Определить: 1) постоянную d дифракционной решетки; 2) число п штрихов на 1 см; 3) число максимумов, которое при этом дает дифракционная решетка; 4) максимальный угол jmах отклонения лучей, соответствующих последнему дифракционному максимуму.
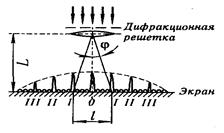
Решение 1. Постоянная d дифракционной решетки, длина волны l и угол j отклонения лучей, соответствующий k-му дифракционному максимуму, связаны соотношением

где k — порядок спектра, или в случае монохроматического света порядок максимума.
В данном случае k = 1, sin j = tg j (ввиду того, что l/2 << L), tg j = ( l /2) L (следует из рис.). С учетом последних трех равенств соотношение (1) примет вид
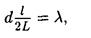
откуда постоянная решетки
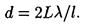
Подставляя данные, получим
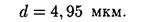
2. Число штрихов на 1 см найдем из формулы
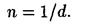
После подстановки числовых значений получим
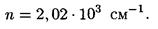
3. Для определения числа максимумов, даваемых дифракционной решеткой, вычислим сначала максимальное значение kmax, исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°.
Из формулы (1) запишем

Подставляя сюда значения величин, получим
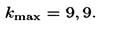
Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значении sinj должен быть больше единицы, что невозможно. Следовательно, kmax = 9.
Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному kmax, т. е. всего 2kmax. Если учесть также центральный нулевой максимум, получим общее число максимумов
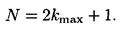
Подставляя значение kmax, найдем
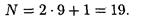
4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выразим из соотношения (2) синус этого угла:
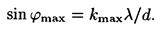
Отсюда
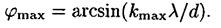
Подставив сюда значения величин l , d , kmax и произведя вычисления, получим
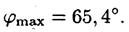
Пример 9. Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны l=500нм.
Принимая Солнце за абсолютно черное тело, определить; 1) энергетическую светимость 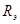 Солнца; 2) поток энергии Фе, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.
Солнца; 2) поток энергии Фе, излучаемый Солнцем; 3) массу m электромагнитных волн (всех длин), излучаемых Солнцем за 1 с. 
Решение. 1. Энергетическая светимость 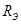 абсолютно черного тела выражается формулой Стефана - Больцмана
абсолютно черного тела выражается формулой Стефана - Больцмана
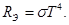 (1)
(1)
Температура излучающей поверхности может быть определена из закона смещения Вина: 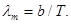 Выразив отсюда температуру Т и подставив ее в формулу (1), получим
Выразив отсюда температуру Т и подставив ее в формулу (1), получим
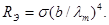 (2)
(2)
Произведя вычисления по формуле (2),найдем
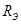 =64 МВт/ м2.
=64 МВт/ м2.
2. Поток энергии 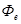 излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:
излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности:
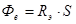 , или
, или 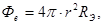 (3)
(3)
где r -радиус Солнца.
Подставив в формулу (3) значения p, r и 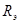 и произведя вычисления, получим
и произведя вычисления, получим
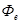 =3,1 . 1026 Вт.
=3,1 . 1026 Вт.
3. Массу электромагнитных волн (всех длин), излучаемых Солнцем за время t=1c, определим, применив закон пропорциональности массы и энергии Е=mс 2. Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии Ф (мощности излучения) на время: E=Ф.t. Следовательно, Фе = mc2, откуда m = Фе / с2.
Произведя вычисления по этой формуле, найдем
m = 4,3 . 109 кг.
Пример 10. Длина волны lm, на которую приходится максимум энергии в спектре излучения абсолютно черного тела, равна 0,58 мкм. Определить максимальную спектральную плотность энергетической светимости (R l,Т)max, рассчитанную на интервал длин волн 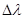 = 1 нм, вблизи
= 1 нм, вблизи 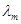 .
.
Решение. Максимальная спектральная плотность энергетической светимости пропорциональна пятой степени температуры Кельвина и выражается формулой
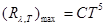 (1)
(1)
Температуру Т выразим из закона смещения Вина
lm=b / T, откуда Т=b /lm.
Подставив полученное выражение температуры в формулу (1), найдем
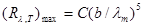 (2)
(2)
Табличное значение С дано в единицах СИ, в которых единичный интервал длин волн 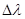 = 1м. По условию же задачи требуется вычислить спектральную плотность энергетической светимости, рассчитанную на интервал длин волн 1 нм, поэтому выпишем значение С в единицах СИ и пересчитаем его на заданный интервал длин волн:
= 1м. По условию же задачи требуется вычислить спектральную плотность энергетической светимости, рассчитанную на интервал длин волн 1 нм, поэтому выпишем значение С в единицах СИ и пересчитаем его на заданный интервал длин волн:
С=1,3.10-5 Вт/(м3.К5 ) = 1,30. 10-5 Вт/(м2 . м . К5) = 1,30.10-14 Вт/(м2. Нм. К5).
Вычисление по формуле (2) дает
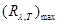 =40,6 кВт/(м . нм).
=40,6 кВт/(м . нм).
Пример 11. Пучок монохроматического света с длиной волны 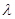 =663нм падает нормально на зеркальную плоскую поверхность. Поток энергии
=663нм падает нормально на зеркальную плоскую поверхность. Поток энергии 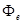 =0,6Вт. Определить силу F давления, испытываемую этой поверхностью, а также число N фотонов, падающих на нее за время t = 5 с.
=0,6Вт. Определить силу F давления, испытываемую этой поверхностью, а также число N фотонов, падающих на нее за время t = 5 с.
Решение. Сила светового давления на поверхность равна произведению светового давления р на площадь S поверхности:
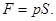 (1)
(1)
Световое давление может быть найдено по формуле
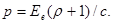 (2)
(2)
Подставляя выражение (2) давления света в формулу (1), получим
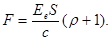 (3)
(3)
Так как произведение облученности 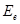 на площадь S поверхности равно потоку Ф энергии излучения, падающего на поверхность, то соотношение (3) можно записать в виде
на площадь S поверхности равно потоку Ф энергии излучения, падающего на поверхность, то соотношение (3) можно записать в виде 
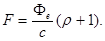
После подстановки значений 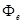 и с учетом, что
и с учетом, что 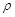 =1 (поверхность зеркальная), получим
=1 (поверхность зеркальная), получим
F= 4 нН.
Число N фотонов, падающих за время 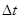 на поверхность, определяется по формуле
на поверхность, определяется по формуле
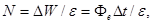
где 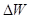 - энергия излучения, получаемая поверхностью за время
- энергия излучения, получаемая поверхностью за время 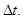
Выразив в этой формуле энергию фотона через длину волны 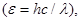
 получим
получим
N=1019 фотонов.
Пример 12. Параллельный пучок света длиной волны 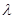 = 500 нм падает нормально на зачерненную поверхность, производя давление р=10 мкПа. Определить: 1) концентрацию n фотонов в пучке; 2) число n1 фотонов, падающих на поверхность площадью 1 м2 за время 1с.
= 500 нм падает нормально на зачерненную поверхность, производя давление р=10 мкПа. Определить: 1) концентрацию n фотонов в пучке; 2) число n1 фотонов, падающих на поверхность площадью 1 м2 за время 1с.
Решение. 1. Концентрация n фотонов в пучке может быть найдена, как частное от деления объемной плотности энергии w на энергию 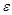 одного фотона:
одного фотона:
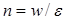 (1)
(1)
Из формулы 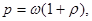 определяющей давление света, где
определяющей давление света, где 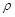 - коэффициент отражения, найдем
- коэффициент отражения, найдем
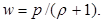 (2)
(2)
Подставив выражение для 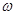 из уравнения (2) в формулу (1), получим
из уравнения (2) в формулу (1), получим
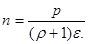 (3)
(3)
Энергия фотона зависит от частоты 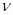 , а следовательно, и от длины световой волны
, а следовательно, и от длины световой волны 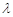 :
:
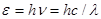 . (4)
. (4)
Подставив выражение для энергии фотона в формулу (3), определим искомую концентрацию фотонов:
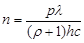 . (5)
. (5)
Коэффициент отражения 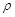 для зачерненной поверхности принимаем равным нулю.
для зачерненной поверхности принимаем равным нулю.
Подставив числовые значения в формулу (5), получим
n=2,52 . 1 013 м-3.
2. Число 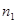 фотонов, падающих на поверхность площадью
фотонов, падающих на поверхность площадью
1м2 за время 1с, найдем из соотношения 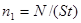 , где N- число фотонов, падающих за время t на поверхность площадью S. Но
, где N- число фотонов, падающих за время t на поверхность площадью S. Но 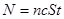 , следовательно,
, следовательно,
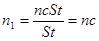 .
.
Подставив сюда значения n и с, получим
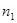 = 7,56. 1021 м-2 . с-1.
= 7,56. 1021 м-2 . с-1.
Пример 13. Определить максимальную скорость 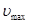 фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовым излучением с длиной волны
фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовым излучением с длиной волны 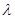 = 0,155мкм.
= 0,155мкм.
Решение. Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта:
. 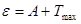 (1)
(1)
Энергия фотона вычисляется по формуле 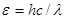 , работа выхода А по таблице для серебра А = 4,7 эВ.
, работа выхода А по таблице для серебра А = 4,7 эВ.
Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена или по классической формуле
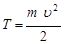 , (2)
, (2)
или по релятивистской
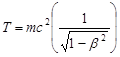 , (3)
, (3)
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект; если энергия фотона 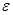 много меньше энергии покоя электрона ,
много меньше энергии покоя электрона , 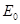 то может быть применена формула (2); если же
то может быть применена формула (2); если же 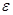 сравнима по размеру с
сравнима по размеру с 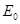 , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3).
, то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3).
В формулу энергии фотона 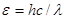 подставим значения величин h, c и
подставим значения величин h, c и 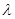 , и произведя вычисления, для ультрафиолетового излучения получим
, и произведя вычисления, для ультрафиолетового излучения получим
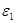 = 1,28аДж = 8эВ.
= 1,28аДж = 8эВ.
Это значение энергии фотона много меньше энергии покоя электрона (0,51МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть выражена по классической формуле (2) 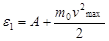 , откуда
, откуда
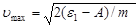 . (4)
. (4)
Выпишем величины, входящие в формулу (4):
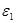 = 1,28 . 10-18 Дж (вычислено выше);
= 1,28 . 10-18 Дж (вычислено выше);
А = 4,7эВ = 4.7 . 1,6 . 10-19 Дж = 0,75 . 10-18 Дж;
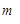 = 9,11 . 10-31 кг.
= 9,11 . 10-31 кг.
Подставив числовые значения в формулу (4), найдем максимальную скорость:
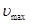 = 1,08 Мм/с.
= 1,08 Мм/с.
Пример 14. Определить красную границу 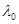 фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны
фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны 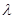 =400 нм максимальная скорость
=400 нм максимальная скорость 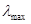 фотоэлектронов равна 0,65 Мм/с.
фотоэлектронов равна 0,65 Мм/с.
Решение. При облучении светом, длина волны 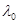 которого соответствует красной границе фотоэффекта, скорость, а следовательно, и киниетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта
которого соответствует красной границе фотоэффекта, скорость, а следовательно, и киниетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта 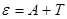 в случае красной границы запишется в виде
в случае красной границы запишется в виде
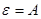 , или
, или 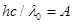
Отсюда

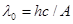 . (1)
. (1)
Работу выхода для цезия определим с помощью уравнения Эйнштейна
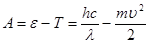 . (2)
. (2)
Выпишем числовые значения величин, выразив их в СИ:
h = 6,62 . 10-34 Дж.с; с = 3 . 108 м/с; 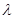 = 400 нм = 4.10-7м;
= 400 нм = 4.10-7м;
m = 9,11.10-31 кг; 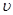 = 6,5. 105 м/с.
= 6,5. 105 м/с.
Подставив эти значения величин в формулу (2) и вычислив, получим
А = 3,05. 10-19 Дж .
Для определения красной границы фотоэффекта подставим значения А,h и с в формулу (1) и вычислим:
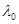 = 651 нм.
= 651 нм.
Пример 15. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол 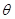 = 90o. Энергия
= 90o. Энергия 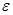 ' рассеянного фотона равна 0,4МэВ. Определить энергию
' рассеянного фотона равна 0,4МэВ. Определить энергию 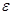 фотона до рассеяния.
фотона до рассеяния.
Решение. Для определения первичного фотона воспользуемся формулой Комптона в виде
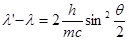 . (1)
. (1)
Формулу (1) преобразуем следующим образом: 1) выразим длины волн 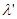 и
и 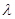 через энергии
через энергии 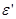 и
и 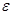 соответствующих фотонов, воспользовавшись соотношением
соответствующих фотонов, воспользовавшись соотношением 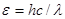 ; 2) умножим числитель и знаменатель правой части формулы на с. Тогда получим
; 2) умножим числитель и знаменатель правой части формулы на с. Тогда получим
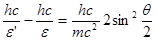 .
.
Сократив на hc, выразим из этой формулы искомую энергию:
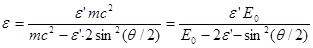 (2)
(2)
где 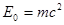 - энергия покоя электрона.
- энергия покоя электрона.
Вычисления по формуле (2) удобнее вести во внесистемных единицах. Взяв из таблицы значение энергии покоя электрона в мегаэлектрон-вольтах и подставив числовые данные, получим
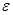 =1,85МэВ.
=1,85МэВ.
Пример 16. Вычислить радиус первой орбиты атома водорода (боровский радиус) и скорость электрона на этой орбите.
Решение. Согласно теории Бора, радиус r электронной орбиты и скорость 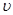 электрона на ней связаны равенством
электрона на ней связаны равенством 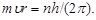 Так как в задаче требуется определить величины, относящиеся к первой орбите, то главное квантовое число n = 1 и указанное выше равенство примет вид
Так как в задаче требуется определить величины, относящиеся к первой орбите, то главное квантовое число n = 1 и указанное выше равенство примет вид
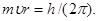 (1)
(1)
Для определения двух неизвестных величин r и 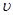 необходимо еще одно уравнение. В качестве второго уравнения воспользуемся уравнением движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщает электрону центростремительное ускорение. На основании второго закона Ньютона можем записать
необходимо еще одно уравнение. В качестве второго уравнения воспользуемся уравнением движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщает электрону центростремительное ускорение. На основании второго закона Ньютона можем записать
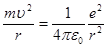
(e и m - заряд и масса электрона), или
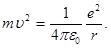 (2)
(2)
Совместное решение равенств (1) и (2) относительно r дает
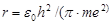 .
.
Подставив сюда значения h, e, m и произведя вычисления, найдем боровский радиус:
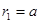 = 5,29 . 10-11м.
= 5,29 . 10-11м.
Из равенства (1) получим выражение скорости электрона на первой орбите:
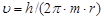 .
.
Произведя вычисления по этой формуле, найдем
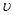 = 2,18 Мм/с.
= 2,18 Мм/с.
Пример 17. Определить энергию 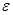 фотона, соответствующего второй линии в первой инфракрасной серии (серии Пашена) атома водорода.
фотона, соответствующего второй линии в первой инфракрасной серии (серии Пашена) атома водорода.
Решение. Энергия 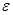 фотона, излучаемого атомом водорода при переходе электрона с одной орбиты на другую,
фотона, излучаемого атомом водорода при переходе электрона с одной орбиты на другую,
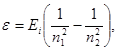
где Ei - энергия ионизации атома водорода; n1 = 1, 2, 3, . . . - номер орбиты, на которую переходит электрон; n2 = n1 +1; n1 + 2;
. . . ; n1 + m -номер орбиты, с которой переходит электрон;
m - номер спектральной линии в данной серии. Для серии Пашена n1 = 3; для второй линии этой серии m =2, n2 = n1 + m = 3 + 2 = 5.
Подставив числовые значения, найдем энергию фотона:
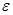 = 0,97 эВ.
= 0,97 эВ.
Пример 18. Определить потенциал 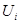 ионизации и первый потенциал возбуждения атома водорода
ионизации и первый потенциал возбуждения атома водорода 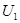 .
.
Решение. Потенциалом ионизации U1 называют ту наименьшую разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с данным невозбужденным атомом ионизировать его. Работа по удалению электрона из атома Ai равна работе сил электрического поля, ускоряющего электрон. 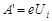 , поэтому
, поэтому
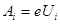 (1)
(1)
Учитывая квантовый характер поглощения энергии атомом; можно сказать ,что работа ионизации Ai равна кванту энергии 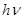 , поглощенному атомом водорода при переходе электрона с первой боровской орбиты на бесконечно удаленную орбиту. Тогда, применив формулу Бальмера-Ритца и положив в ней n1 =1, n2 =
, поглощенному атомом водорода при переходе электрона с первой боровской орбиты на бесконечно удаленную орбиту. Тогда, применив формулу Бальмера-Ритца и положив в ней n1 =1, n2 = 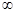 , получим
, получим
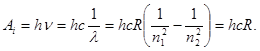 (2)
(2)
Теперь из (1), (2) найдем
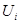 = 13,6 В
= 13,6 В
Первый потенциал возбуждения U1 есть та наименьшая разность потенциалов, которую должен пройти в ускоряющем поле электрон, чтобы при столкновении с невозбужденным атомом перевести его в первое возбужденное состояние. Для атома водорода это соответствует переходу электрона с первой боровской орбиты на вторую. Снова приравняв работу сил ускоряющего электрического поля 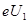 кванту энергии
кванту энергии 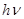 , поглощенному атомом при переходе в первое возбужденное состояние, и положив n1=1, n2=2, получим
, поглощенному атомом при переходе в первое возбужденное состояние, и положив n1=1, n2=2, получим
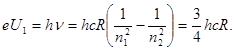
Отсюда
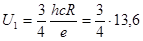 В = 10,2 В.
В = 10,2 В.
Пример 19. Определить начальную активность 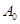 радиоактивного магния
радиоактивного магния 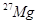 массой m=0,2мкг, а также активность A по истечению времени t = 1 ч. Предполагается, что все атомы изотопа радиоактивны.
массой m=0,2мкг, а также активность A по истечению времени t = 1 ч. Предполагается, что все атомы изотопа радиоактивны.
Решение. Начальная активность изотопа
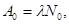 (1)
(1)
где 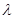 -постоянная радиоактивного распада; N0 - количество атомов изотопа в начальный момент( t = 0 ).
-постоянная радиоактивного распада; N0 - количество атомов изотопа в начальный момент( t = 0 ).
Если учесть, что 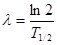 ,
, 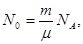 то формула (1) примет вид
то формула (1) примет вид
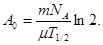 (2)
(2)
Выразим входящие в эту формулу величины в СИ и произведем вычисления:
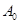 = 5,15 . 1012Бк .
= 5,15 . 1012Бк .
Активность изотопа уменьшается со временем по закону
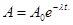 (3)
(3)
Заменив в Формуле (3) постоянную распада 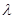 ее выражением, получим
ее выражением, получим
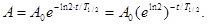
Так как 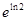 =2, то окончательно будем иметь
=2, то окончательно будем иметь
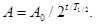
Сделав подстановку числовых значений, получим
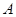 = 8,05 . 1010Бк .
= 8,05 . 1010Бк .
Пример 20. При определении периода полураспада T1/2 короткоживущего радиоактивного изотопа использован счетчик импульсов. За время 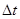 = 1 мин в начале наблюдения ( t = 0) было насчитано
= 1 мин в начале наблюдения ( t = 0) было насчитано 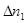 =250 импульсов, а по истечению времени t = 1 ч -
=250 импульсов, а по истечению времени t = 1 ч - 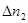 = 92 импульса. Определить постоянную радиоактивного распада
= 92 импульса. Определить постоянную радиоактивного распада 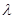 и период полураспада
и период полураспада 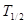 изотопа.
изотопа.
Решение. Число импульсов 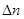 , регистрируемых счетчиком за время
, регистрируемых счетчиком за время 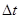 , пропорционально числу распавшихся атомов
, пропорционально числу распавшихся атомов 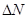 . Таким образом, при первом измерении
. Таким образом, при первом измерении
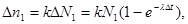 (1)
(1)
где 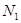 - количество радиоактивных атомов к моменту начала отсчета; k - коэффициент пропорциональности (постоянный для данного прибора и данного расположения прибора относительно радиоактивного изотопа).
- количество радиоактивных атомов к моменту начала отсчета; k - коэффициент пропорциональности (постоянный для данного прибора и данного расположения прибора относительно радиоактивного изотопа).
При повторном измерении (предполагается, что расположение приборов осталось прежним)
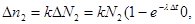 (2)
(2)
где N2 - количество радиоактивных атомов к моменту начала второго измерения.
Разделив соотношение (1) на выражение (2) и приняв во внимание, что по условию задачи 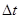 одинаково в обоих случаях, а также, что N1 и N2 связаны между собой соотношением
одинаково в обоих случаях, а также, что N1 и N2 связаны между собой соотношением 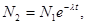 получим
получим
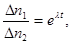 (3)
(3)
где t - время от первого до второго измерения. Для вычисления  выражение (3)следует прологарифмировать:
выражение (3)следует прологарифмировать: 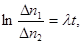 откуда
откуда
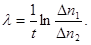
Подставив числовые данные, получим постоянную радиоактивного распада, а затем и период полураспада
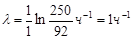 ;
;
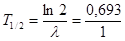 ч = 0,693 ч = 41,5мин.
ч = 0,693 ч = 41,5мин.
Пример 21. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля 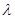 для двух случаев: 1)
для двух случаев: 1) 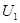 = 51 В; 2)
= 51 В; 2) 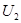 = 510кВ.
= 510кВ.
Решение. Длина волны де Бройля 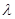 частицы зависит от ее импульса p и определяется формулой
частицы зависит от ее импульса p и определяется формулой
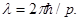 (1)
(1)
Импульс частицы можно определить, если известна ее кинетическая энергия T . Связь импульса с кинетической энергией для нерелятивистского ( когда 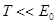 ) и для релятивистского ( когда
) и для релятивистского ( когда 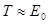 ) случаев соответственно выражается формулами:
) случаев соответственно выражается формулами:
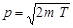 ; (2)
; (2)
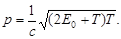 (3)
(3)
Формула (1) с учетом соотношений (2) и (3) запишется соответственно в нерелятивистском и релятивистском случаях:
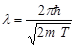 ; (4)
; (4)
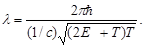 (5)
(5)
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов 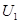 =51В и
=51В и 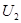 = 510кВ, с энергией покоя электрона и в зависимости от этого решим вопрос, которую из формул (4) и (5) следует применить для вычисления длины волны де Бройля.
= 510кВ, с энергией покоя электрона и в зависимости от этого решим вопрос, которую из формул (4) и (5) следует применить для вычисления длины волны де Бройля.
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U ,
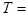
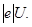
В первом случае 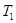 =
= 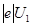 = 51эВ = 0,51 . 10-4МэВ, что много меньше энергии покоя электрона
= 51эВ = 0,51 . 10-4МэВ, что много меньше энергии покоя электрона 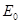
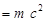 = 0,51МэВ. Следовательно, можно применить формулу(4).
= 0,51МэВ. Следовательно, можно применить формулу(4).
Для упрощения расчетов заметим, что 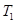 =10-4
=10-4 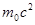 . Подставив это выражение в формулу(4), перепишем ее в виде
. Подставив это выражение в формулу(4), перепишем ее в виде
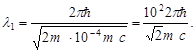
Учтя, что 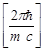 есть комптоновская длина волны
есть комптоновская длина волны 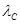 , получим
, получим
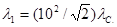
Так как 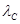 = 2,43 . 10-12) м, то
= 2,43 . 10-12) м, то
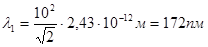 .
.
Во втором случае кинетическая энергия 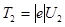 = 150 кэВ = 0,51 МэВ, т.е. равна энергии покоя электрона. Следовательно, необходимо применить релятивистскую формулу (5).
= 150 кэВ = 0,51 МэВ, т.е. равна энергии покоя электрона. Следовательно, необходимо применить релятивистскую формулу (5).
Учтя, что 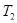 = 0,51 МэВ =
= 0,51 МэВ = 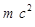 , по формуле (5) найдем
, по формуле (5) найдем
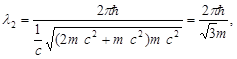 или
или 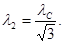
Подставив значение 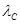 в последнюю формулу и произведя вычисления, получим
в последнюю формулу и произведя вычисления, получим
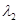 = 1,4 пм.
= 1,4 пм.
Пример 22. Кинетическая энергия T электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
Решение. Неопределенность координаты и импульса электрона связаны соотношением
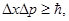 (1)
(1)
где 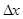 -неопределенность координаты электрона;
-неопределенность координаты электрона; 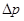 - неопределенность его импульса.
- неопределенность его импульса.
Из этого соотношения следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью: 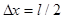 . Соотношение неопределенностей (1) можно записать в этом случае в виде
. Соотношение неопределенностей (1) можно записать в этом случае в виде
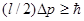 ,откуда
,откуда
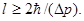 (2)
(2)
Физически разумная неопределенность импульса 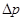 , во всяком случае, не должна превышать значения самого импульса p, т.е
, во всяком случае, не должна превышать значения самого импульса p, т.е 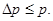
Импульс p связан с кинетической энергией T соотношением: 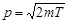 . Заменим
. Заменим 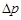 значением
значением 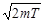 ( такая замена не увеличит
( такая замена не увеличит 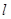 ). Переходя от неравенства (2) к равенству,
). Переходя от неравенства (2) к равенству,
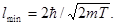
Подставив числовые значения и произведя вычисления, найдем
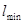 = 124 пм.
= 124 пм.
Пример 23. В баллоне вместимостью V = 6,9 л находится азот массой m = 2,3 г. При нагревании часть молекул диссоциировали на атомы. Степень диссоциации 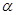 = 0,2. Определить: 1) общее число
= 0,2. Определить: 1) общее число 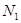 молекул и концентрацию
молекул и концентрацию 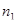 молекул азота до нагревания;2) концентрацию
молекул азота до нагревания;2) концентрацию 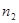 молекул и
молекул и 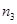 атомов азота после нагревания.
атомов азота после нагревания.
Решение. По определению, концентрация частиц газа есть отношение числа частиц к вместимости сосуда, занимаемого газом:
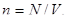 (1)
(1)
1. Число 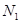 молекул газа до нагревания найдем из соотношения
молекул газа до нагревания найдем из соотношения
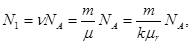 (2)
(2)
где 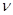 - количество вещества азота;
- количество вещества азота; 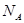 - постоянная Авогадро;
- постоянная Авогадро; 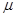 - молярная масса азота;
- молярная масса азота; 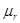 - относительная молекулярная масса азота; k =10-3 кг/моль.
- относительная молекулярная масса азота; k =10-3 кг/моль.
Подставив значения величин в (2), получим
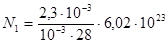 молекул = 4,94 . 1023 молекул.
молекул = 4,94 . 1023 молекул.
Концентрацию 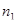 найдем, подставив значения величин в (1):
найдем, подставив значения величин в (1):
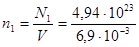 м-3 =7,16. 1025 м-3.
м-3 =7,16. 1025 м-3.
2. Концентрацию после нагревания найдем из соотношения
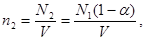 (3)
(3)
где 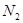 - число молекул, не распавшихся на атомы.
- число молекул, не распавшихся на атомы.
После подстановки значений величин в (3) получим
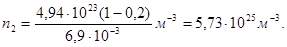
Концентрация атомов после нагревания азота
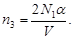 (4)
(4)
Число 2 в формуле (4) выражает тот факт, что каждая молекула после распада дает два атома.
Подставим в (4) значения величин и произведем вычисления: 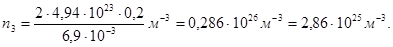
Пример 24. В колбе вместимостью V = 0,5 л находится кислород при нормальных условиях. Определить среднюю энергию 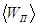 поступательного движения всех молекул, содержащихся в колбе.
поступательного движения всех молекул, содержащихся в колбе.
Решение. Средняя энергия 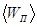 поступательного движения всех молекул может быть выражена соотношением
поступательного движения всех молекул может быть выражена соотношением
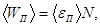 (1)
(1)
где 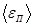 - средняя энергия поступательного движения одной молекулы; N - число всех молекул, содержащихся в колбе.
- средняя энергия поступательного движения одной молекулы; N - число всех молекул, содержащихся в колбе.
Как известно,
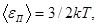 (2)
(2)
где k - постоянная Больцмана; T - термодинамическая температура.
Число молекул, содержащихся в колбе, найдем по формуле
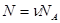 , (3)
, (3)
где 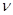 - количество вещества кислорода;
- количество вещества кислорода; 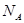 - постоянная Авогадро.
- постоянная Авогадро.
Количество вещества 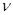 найдем из таких соображений: известно, что при нормальных условиях молярный объем
найдем из таких соображений: известно, что при нормальных условиях молярный объем 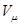 равен 22.4 . 10-3 м3/моль. Так как, по условию задачи, кислород в колбе находится при нормальных условиях, то количество вещества кислорода в колбе выражается соотношением
равен 22.4 . 10-3 м3/моль. Так как, по условию задачи, кислород в колбе находится при нормальных условиях, то количество вещества кислорода в колбе выражается соотношением
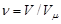 . (4)
. (4)
Подставив выражение 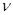 по (4) в (3) , получим
по (4) в (3) , получим
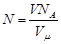 . (5)
. (5)
С учетом (2) и (5) выражение (1) энергии поступательного движения молекул примет вид
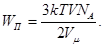 (6)
(6)
Проверим, дает ли правая часть расчетной формулы единицу энергии (джоуль). Для этого вместо символов величин подставим единицы, в которых эти величины выражаются:
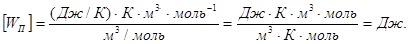
Подставив значения величин в (6) и произведя вычисления, найдем
. 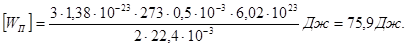
Пример 25. Средняя длина свободного пробега 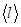 молекулы углекислого газа при нормальных условиях равна 40нм. Определить среднюю арифметическую скорость
молекулы углекислого газа при нормальных условиях равна 40нм. Определить среднюю арифметическую скорость 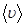 молекул и число z соударений, которые испытывает молекула в 1 с.
молекул и число z соударений, которые испытывает молекула в 1 с.
Решение. Средняя скорость молекул определяется по формуле
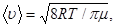
где 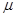 - молярная масса вещества.
- молярная масса вещества.
Подставив числовые значения, получим
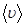 = 362 м/с.
= 362 м/с.
Среднее число 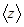 соударений молекулы в 1 с определяется отношением средней скорости
соударений молекулы в 1 с определяется отношением средней скорости 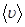 молекулы к средней длине ее свободного пробега
молекулы к средней длине ее свободного пробега 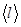 :
:
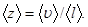
Подставив в эту формулу значения 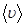 = 362 м/с,
= 362 м/с, 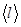 = 4нм= 4 . 10-8 м, получим
= 4нм= 4 . 10-8 м, получим
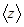 =9,05 . 109 с-1.
=9,05 . 109 с-1.
Пример 26. Два тонкостенных коаксиальных цилиндра длиной l=10см могут свободно вращаться вокруг их общей оси z. Радиус R большого цилиндра равен 5 см. Между цилиндрами имеется зазор размером d=2мм. Оба цилиндра находятся в воздухе при нормальных условиях. Внутренний цилиндр приводят во вращение с постоянной частотой 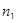 =20 Гц. Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту вращения
=20 Гц. Внешний цилиндр заторможен. Определить, через какой промежуток времени с момента освобождения внешнего цилиндра он приобретет частоту вращения 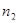 =1 Гц. При расчетах изменением относительной скорости цилиндров пренебречь. Масса m внешнего цилиндра равна 100г.
=1 Гц. При расчетах изменением относительной скорости цилиндров пренебречь. Масса m внешнего цилиндра равна 100г.
Решение .При вращении внутреннего цилиндра слой воздуха увлекается им и начинает участвовать во вращательном движении. Вблизи поверхности этого цилиндра слой воздуха приобретает со временем практически такую же линейную скорость, как и скорость точек на поверхности цилиндра,т.е. 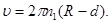 Так как
Так как 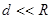 , то приближенно можно считать
, то приближенно можно считать
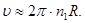 (1)
(1)
Вследствие внутреннего трения момент импульса передается соседним слоям газа и в конечном счете внешнему цилиндру. За интервал времени 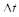 внешний цилиндр приобретает момент импульса
внешний цилиндр приобретает момент импульса 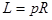 , где p - импульс, полученный за
, где p - импульс, полученный за 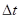 внешним цилиндром. Отсюда,
внешним цилиндром. Отсюда,
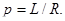 . (2)
. (2)
С другой стороны,
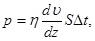 (3)
(3)
где 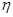 - динамическая вязкость;
- динамическая вязкость; 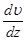 - градиент скорости; S - площадь поверхности цилиндра
- градиент скорости; S - площадь поверхности цилиндра 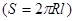 .
.
Приравняв правые части выражений (2) и (3) и выразив из полученного равенства искомый интервал 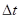 , получим
, получим
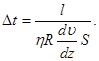 (4)
(4)
Найдем входящие в эту формулу величины L, 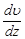 и S. Момент импульса
и S. Момент импульса 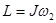 ,где
,где 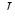 момент инерции цилиндра
момент инерции цилиндра 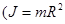 ); m -его масса;
); m -его масса; 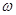 - угловая скорость внешнего цилиндра
- угловая скорость внешнего цилиндра 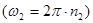 . С учетом этого запишем
. С учетом этого запишем
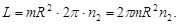
Градиент скорости 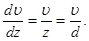 Площадь цилиндра равна
Площадь цилиндра равна 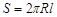 .
.
Подставив в (4) выражение 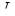 ,
, 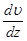 , S, получим
, S, получим
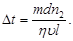
Заменив здеь 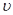 по (1), найдем
по (1), найдем
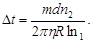 (5)
(5)
Динамическая вязкость воздуха
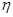 = 17,2 мкПа . с = 1,72 . 10-5 Па . с.
= 17,2 мкПа . с = 1,72 . 10-5 Па . с.
Подставив в (5) значения входящих в нее величин и произведя вычисления, получим
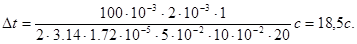
Пример 27. Определить коэффициенты диффузии и внутреннего трения азота, находящегося при температуре Т = 300 К и давлении 105 Па.
Решение. Коэффициент диффузии определяется по формуле
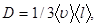 (1)
(1)
где 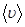 средняя арифметическая скорость молекул, равная
средняя арифметическая скорость молекул, равная
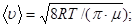 (2)
(2)
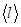 - средняя длина свободного пробега молекул. Для нахождения
- средняя длина свободного пробега молекул. Для нахождения 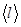 воспользуемся формулой
воспользуемся формулой
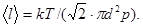 (3)
(3)
Подставляя (2) и (3) в выражение (1), имеем
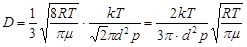 . (4)
. (4)
Коэффициент внутреннего трения
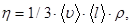 (5)
(5)
где 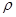 - плотность газа при температуре 300 К и давлении
- плотность газа при температуре 300 К и давлении
105 Па. Для нахождения 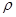 воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота - при нормальных условиях
воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота - при нормальных условиях 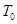 = 273 К, р = 1,01 . 105 Па и в условиях задачи:
= 273 К, р = 1,01 . 105 Па и в условиях задачи:
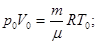
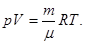 (6)
(6)
Учитывая, что 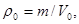
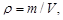 - имеем
- имеем
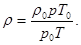 (7)
(7)
Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии
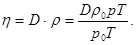 (8)
(8)
Подставляя числовые значения в (4) и (8), получим
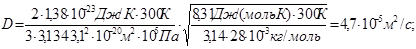
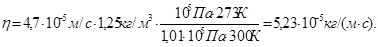
Пример 28. Пылинки массой m = 10-18 г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура T воздуха во всем объеме одинакова и равна 300 К.
Решение. При равновесном распределении пылинок концентрация их зависит только от координаты z по оси, направленной вертикально. В этом случае к распределению пылинок можно применить формулу Больцмана
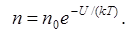 (1)
(1)
Так как в однородном поле силы тяжести 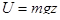 , то
, то
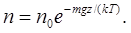 (2)
(2)
По условию задачи, изменение 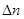 концентрации с высотой мало по сравнению с
концентрации с высотой мало по сравнению с 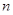
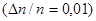 , поэтому без существенной погрешности изменение концентрации
, поэтому без существенной погрешности изменение концентрации 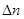 можно заменить дифференциалом
можно заменить дифференциалом 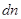 .
.
Дифференцируя выражение (2) по z, получим
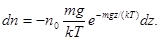
Так как 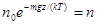 , то
, то
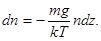
Отсюда находим интересующее нас изменение координаты:
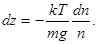
Знак минус показывает, что положительным изменениям координаты 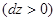 соответствует уменьшение относительной концентрации
соответствует уменьшение относительной концентрации 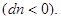 Знак минус опустим (в данном случае он несуществен) и заменим дифференциалы
Знак минус опустим (в данном случае он несуществен) и заменим дифференциалы 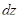 и
и 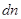 конечными приращениями
конечными приращениями  и
и 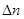 :
:
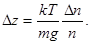
Подставим в эту формулу значения величин 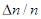 = 0,01,
= 0,01, 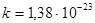 Дж/К, T = 300 К, m = 10-21 кг,
Дж/К, T = 300 К, m = 10-21 кг, 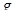 = 9,81 м/с и, произведя вычисления, найдем
= 9,81 м/с и, произведя вычисления, найдем
 = 4,23 мм.
= 4,23 мм.
Как видно из полученного результата, концентрация даже таких маленьких пылинок (m = 10-18 г) очень быстро изменяется с высотой.
Пример 29. В сосуде содержится газ, количество вещества 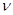 которого равно 1,2 моль. Рассматривая этот газ как идеальный, определить число
которого равно 1,2 моль. Рассматривая этот газ как идеальный, определить число 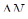 молекул, скорости u которых меньше 0,001 наиболее вероятной скорости
молекул, скорости u которых меньше 0,001 наиболее вероятной скорости 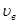 .
.
Решение. Для решения задачи удобно воспользоваться распределением молекул по относительным скоростям u (u = 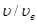 ). Число
). Число 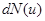 молекул, относительные скорости u которых заключены в пределах от u до du, определяется формулой
молекул, относительные скорости u которых заключены в пределах от u до du, определяется формулой
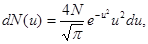 (1)
(1)
где N - полное число молекул.
По условию задачи, максимальная скорость интересующих нас молекул 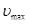 = 0,001. Для таких значений u выражение (1) можно существенно упростить. В самом деле, для u<<1 имеем
= 0,001. Для таких значений u выражение (1) можно существенно упростить. В самом деле, для u<<1 имеем 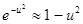 . Пренебрегая значением
. Пренебрегая значением 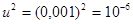 по сравнению с единицей, выражение (1) запишем в виде
по сравнению с единицей, выражение (1) запишем в виде
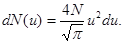 (2)
(2)
Интегрируя это выражение по u в пределах от 0 до 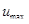 , получим
, получим
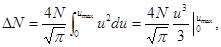 или
или
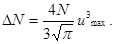 (3)
(3)
Выразим в (3) число молекул N через количество вещества 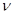 и постоянную Авогадро, найдем расчетную формулу:
и постоянную Авогадро, найдем расчетную формулу:
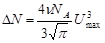 . (4)
. (4)
Подставим в (4) значение величин 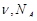 и произведем вычисле ния:
и произведем вычисле ния:
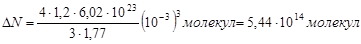
Пример 30. Зная функцию 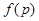 распределения молекул по импульсам, определить среднее значение квадрата импульса
распределения молекул по импульсам, определить среднее значение квадрата импульса 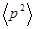 .
.
Решение. Среднее значение квадрата импульса 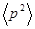 можно определить по общему правилу вычисления среднего:
можно определить по общему правилу вычисления среднего:
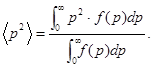 (1)
(1)
Функция распределения молекул по импульсам имеет вид
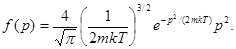 (2)
(2)
Эта функция распределения уже нормирована на единицу, т.е. 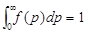 . С учетом нормировки формулу (1) перепишем иначе:
. С учетом нормировки формулу (1) перепишем иначе:
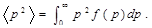 (3)
(3)
Подставим выражение 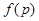 по уравнению (2) в формулу (3) и вынесем величины, не зависящие от p, за знак интеграла:
по уравнению (2) в формулу (3) и вынесем величины, не зависящие от p, за знак интеграла:
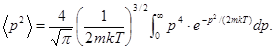 (4)
(4)
Этот интеграл можно привести к табличному
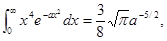 положив
положив 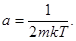
В нашем случае это даст
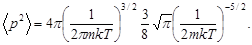
После упрощений и сокращений найдем
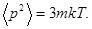
Пример 31. Определить количество теплоты 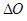 , необходимое для нагревания кристалла
, необходимое для нагревания кристалла 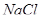 массой m = 20 г на
массой m = 20 г на 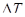 = 2К, в двух случаях, если нагревание происходит от температуры: 1)
= 2К, в двух случаях, если нагревание происходит от температуры: 1) 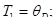 2) T2 = 2 К. Характеристическую температуру Дебая
2) T2 = 2 К. Характеристическую температуру Дебая 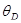 для
для 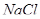 принять равной 320 К.
принять равной 320 К.
Решение. Количество теплоты 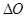 , подводимое для нагревания тела от температуры T1 до T2, может быть вычислено по формуле
, подводимое для нагревания тела от температуры T1 до T2, может быть вычислено по формуле
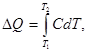 (1)
(1)
где C - теплоемкость тела (системы).
Теплоемкость тела связана с молярной теплоемкостью 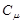 соотношением
соотношением 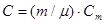 , где
, где 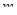 - масса тела;
- масса тела;
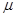 - молярная масса. Подставив это выражение C в формулу (1) получим
- молярная масса. Подставив это выражение C в формулу (1) получим
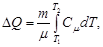 (2)
(2)
В общем случае 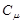 есть функция температуры, поэтому за знак интеграла ее выносить нельзя. Однако в первом случае изменением теплоемкости по сравнению с ее значением при температуре T1 можно пренебречь и считать ее на всем интервале температур
есть функция температуры, поэтому за знак интеграла ее выносить нельзя. Однако в первом случае изменением теплоемкости по сравнению с ее значением при температуре T1 можно пренебречь и считать ее на всем интервале температур 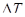 постоянной и равной
постоянной и равной 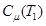 Ввиду этого формула (2) примет вид
Ввиду этого формула (2) примет вид
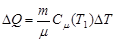 (3)
(3)
Подставляя это значение 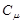 в формулу (3), получим
в формулу (3), получим
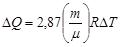 . (4)
. (4)
Произведя вычисления по формуле (4), найдем
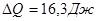 .
.
Во втором случае 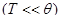 нахождение
нахождение 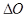 облегчается тем, что можно воспользоваться предельным законом Дебая, в согласии с которым теплоемкость пропорциональна кубу абсолютной температуры. В этом случае теплоемкость сильно изменяется в пределах заданного интервала темпера тур и ее нельзя выносить за знак интеграла в формуле (2).
облегчается тем, что можно воспользоваться предельным законом Дебая, в согласии с которым теплоемкость пропорциональна кубу абсолютной температуры. В этом случае теплоемкость сильно изменяется в пределах заданного интервала темпера тур и ее нельзя выносить за знак интеграла в формуле (2).
Используя выражение предельного закона Дебая
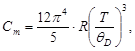 получим
получим
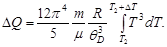
Выполним интегрирование:
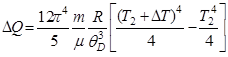 (5)
(5)
С учетом того, что 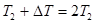 , выражение (5) примет вид
, выражение (5) примет вид
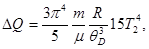 или
или
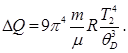
Подставив в последнюю формулу значения величин 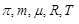 и
и 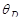 и произведя вычисления, найдем
и произведя вычисления, найдем
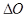 = 1,22мДж.
= 1,22мДж.
Пример 32. Молярная изохорная теплоемкость аргона при температуре 4 К равна 0,174 Дж/моль. К. Определить значение молярной изохорной теплоемкости аргона при температуре 2 К.
Решение. Согласно теории Дебая, теплоемкость кристаллической решетки при низких температурах T, когда 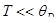 (квантовая область), где
(квантовая область), где 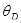 - характеристическая температура Дебая, пропорциональна кубу термодинамической температуры,
- характеристическая температура Дебая, пропорциональна кубу термодинамической температуры,
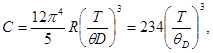 (1)
(1)
где C - молярная изохорная теплоемкость. R - молярная газовая постоянная.
При высоких температурах, когда ( 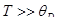 классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти
классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти
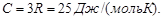 (2) Поскольку при T1 = 4 К теплоемкость аргона
(2) Поскольку при T1 = 4 К теплоемкость аргона
C1 = 0.174 Дж /(моль.К) много меньше, чем 3R = 25 Дж/(мольК),
выполняется закон Т3 Дебая, согласно которому 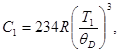
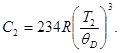 (3)
(3)
Отсюда
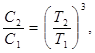 (4)
(4)
или
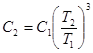 . (5)
. (5)
Подставляя в (5) числовые данные, получим
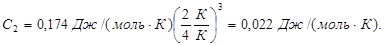
Пример 33. Дебаевская температура кристалла равна 150 К. Определить максимальную частоту колебаний кристаллической решетки. Сколько фононов такой же частоты возбуждается в среднем в кристалле при температуре 300К?
Решение. Дебаевская температура
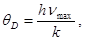 (1)
(1)
где 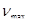 - максимальная частота колебаний кристаллической решетки, h - постоянная Планка; k - постоянная Больцмана.
- максимальная частота колебаний кристаллической решетки, h - постоянная Планка; k - постоянная Больцмана.
Из (1) найдем
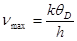 . (2)
. (2)
Подставляя в (2) числовые значения, получаем 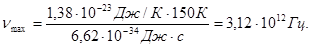
Среднее число фононов с энергией 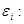
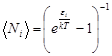 . (3)
. (3)
где T - термодинамическая температура кристалла.
Энергия фонона, соответствующая частоте колебаний 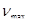 ,
,
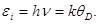 (4)
(4)
Подставляя (4) в (3), находим
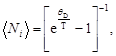
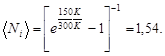
Пример 34. Определить число n узлов, приходящихся на одну элементарную ячейку в гранецентрированной кубической решетке.
Решение. Выделим элементарную ячейку в кубической решетке и определим, скольким соседним элементарным ячейкам принадлежит тот или иной узел выделенной ячейки. В этой ячейке имеются узлы двух типов: А (находящиеся в вершинах куба) и В ( находящиеся на гранях куба в точке пересечения диагоналей).
Узел А принадлежит одновременно восьми элементарным ячейкам. Следовательно, в данную ячейку узел А входит с долей 1/8. Узел В входит одновременно только в две ячейки и, следовательно, в данную ячейку узел В входит с долей ½. Если учесть, что число узлов типа А в ячейке равно восьми, а число узлов типа В равно шести, т.е. числу граней, то общее число узлов, приходящихся на одну элементарную ячейку в гранецентрированной решетке,
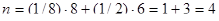 узла.
узла.
Так как число узлов равно числу атомов, то в соответствующей структуре на элементарную ячейку приходится четыре атома.
Пример 35. Определить параметр  решетки и расстояние d между ближайшими соседними атомами кристалла каль ция (решетка гранецентрированная кубической сингонии). Плотность
решетки и расстояние d между ближайшими соседними атомами кристалла каль ция (решетка гранецентрированная кубической сингонии). Плотность 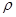 кристалла кальция равна 1,55 . 103 кг/м.
кристалла кальция равна 1,55 . 103 кг/м.
Решение. Параметр  кубической решетки связан с объемом элементарной ячейки соотношением
кубической решетки связан с объемом элементарной ячейки соотношением 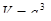 С другой стороны, объем элементарной ячейки равен отношению молярного объема к числу элементарных ячеек в одном моле кристалла:
С другой стороны, объем элементарной ячейки равен отношению молярного объема к числу элементарных ячеек в одном моле кристалла: 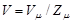 . Приравняв правые части приведенных выражений для V, найдем
. Приравняв правые части приведенных выражений для V, найдем
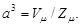 (1)
(1)
Молярный объем кальция 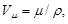 где
где 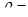 плотность кальция;
плотность кальция; 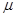 - его молярная масса. Число элементарных ячеек в одном моле
- его молярная масса. Число элементарных ячеек в одном моле
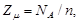
где n - число атомов, приходящихся на одну ячейку. Подставив в формулу (1) приведенные выражения для 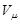 и
и 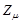 , получим
, получим
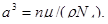
Отсюда
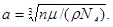 (2)
(2)
Подставим значения величин 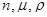 и
и 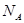 в формулу (2), учитывая, что n = 4. Произведя вычисления, найдем
в формулу (2), учитывая, что n = 4. Произведя вычисления, найдем
 = 556пм.
= 556пм.
Расстояние d между ближайшими соседними атомами находится из простых геометрических соображений
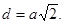
Подставив в это выражение найденное ранее значение  , получим
, получим
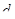 = 393пм.
= 393пм.
Пример 36. Кусок металла объемом 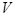 = 20 см3 находится при температуре
= 20 см3 находится при температуре 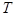 = 0. Определить число
= 0. Определить число 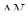 свободных электронов, импульсы которых отличаются от максимального импульса
свободных электронов, импульсы которых отличаются от максимального импульса 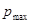 не более чем на 0,1
не более чем на 0,1 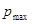 . Энергия Ферми
. Энергия Ферми 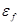 = 5эВ.
= 5эВ.
Решение. Для того чтобы установить распределение свободных электронов в металле по импульсам, воспользуемся распределением Ферми для свободных электронов при 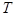 = 0:
= 0:
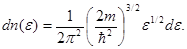 (1)
(1)
Так как 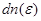 есть число электронов в единице объема, энергии которых заключены в интервале значений от
есть число электронов в единице объема, энергии которых заключены в интервале значений от  до
до 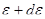 , то оно должно быть равно числу электронов
, то оно должно быть равно числу электронов 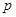 в единице объема, заключенных в интервале значений импульса от
в единице объема, заключенных в интервале значений импульса от 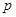 до
до 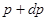 , т.е.
, т.е.
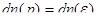 (2)
(2)
При этом должно соблюдаться следующее условие. Данной энергии  соответствует определенный импульс
соответствует определенный импульс
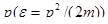 и интервалу энергии
и интервалу энергии 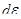 отвечает соответствующий ему интервал импульсов
отвечает соответствующий ему интервал импульсов 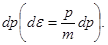 Заметив, что
Заметив, что 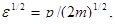 подставим в правую часть равенства (2) вместо
подставим в правую часть равенства (2) вместо 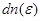 выражение (1) с заменой
выражение (1) с заменой  на
на 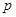 и
и 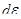 на
на 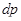 в соответствии с полученными соотношениями, т.е.
в соответствии с полученными соотношениями, т.е.
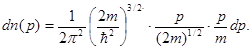
После сокращений получим искомое распределение свободных электронов в металле по импульсам при 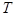 = 0:
= 0:
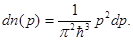
Число электронов в единице объема, импульсы которых заключены в интервале от 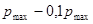 до
до 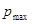 , найдем интегрированием в соответствующих пределах:
, найдем интегрированием в соответствующих пределах:
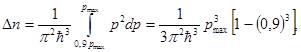
или 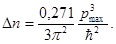
Учитывая, что максимальный импульс 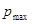 и максимальная энергия
и максимальная энергия  электронов в металле ( при
электронов в металле ( при 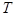 = 0 ) связаны соотношением
= 0 ) связаны соотношением 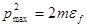 найдем искомое число
найдем искомое число 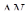 свободных электронов в металле:
свободных электронов в металле:
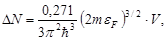
или
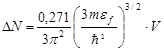 .
.
Подставив значения величин 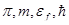 и
и 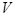 и произведя вычисления
и произведя вычисления 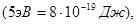 получим
получим 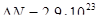 электронов.
электронов.
Таблица вариантов контрольной работы № 2.
| Вариант | Задачи | |||||
| 1 | 42 | 48 | 78 | 124 | 152 | 182 |
| 2 | 43 | 49 | 79 | 125 | 153 | 182 |
| 3 | 1 | 50 | 80 | 126 | 154 | 183 |
| 4 | 2 | 51 | 81 | 127 | 155 | 184 |
| 5 | 3 | 52 | 82 | 128 | 156 | 185 |
| 6 | 4 | 53 | 83 | 129 | 157 | 186 |
| 7 | 5 | 54 | 84 | 130 | 158 | 187 |
| 8 | 6 | 55 | 85 | 131 | 159 | 188 |
| 9 | 7 | 56 | 86 | 132 | 160 | 189 |
| 10 | 8 | 57 | 87 | 133 | 161 | 190 |
| 11 | 9 | 58 | 88 | 134 | 162 | 191 |
| 12 | 10 | 59 | 89 | 135 | 163 | 192 |
| 13 | 11 | 60 | 90 | 136 | 164 | 193 |
| 14 | 12 | 61 | 91 | 137 | 165 | 194 |
| 15 | 13 | 62 | 92 | 138 | 166 | 195 |
| 16 | 14 | 63 | 93 | 139 | 167 | 196 |
| 17 | 15 | 64 | 94 | 140 | 168 | 197 |
| 18 | 16 | 65 | 95 | 141 | 169 | 198 |
| 19 | 17 | 66 | 96 | 142 | 170 | 199 |
| 20 | 18 | 67 | 97 | 143 | 171 | 200 |
| 21 | 19 | 68 | 98 | 144 | 172 | 101 |
| 22 | 20 | 69 | 99 | 145 | 173 | 202 |
| 23 | 21 | 70 | 100 | 146 | 174 | 203 |
| 24 | 22 | 72 | 101 | 147 | 175 | 204 |
| 25 | 23 | 72 | 102 | 148 | 176 | 205 |
| 26 | 24 | 72 | 103 | 149 | 177 | 206 |
| 27 | 25 | 74 | 104 | 150 | 178 | 207 |
| 28 | 26 | 75 | 105 | 151 | 179 | 208 |
| 29 | 27 | 76 | 106 | 124 | 180 | 209 |
| 30 | 28 | 77 | 107 | 125 | 181 | 210 |
| 31 | 29 | 48 | 108 | 126 | 152 | 211 |
| 32 | 30 | 49 | 109 | 127 | 153 | 212 |
| 33 | 31 | 50 | 110 | 128 | 154 | 213 |
| 34 | 32 | 51 | 111 | 129 | 155 | 214 |
| 35 | 33 | 52 | 112 | 130 | 156 | 215 |
| 36 | 34 | 53 | 113 | 131 | 157 | 216 |
| 37 | 35 | 54 | 114 | 132 | 158 | 217 |
| 38 | 36 | 55 | 115 | 133 | 159 | 218 |
| 39 | 37 | 56 | 116 | 134 | 160 | 219 |
| 40 | 38 | 57 | 117 | 135 | 161 | 220 |
| 41 | 39 | 58 | 118 | 136 | 162 | 221 |
| 42 | 40 | 59 | 119 | 137 | 163 | 222 |
| 43 | 41 | 60 | 120 | 138 | 164 | 223 |
| 44 | 42 | 61 | 121 | 139 | 165 | 224 |
| 45 | 43 | 62 | 122 | 140 | 166 | 225 |
| 46 | 44 | 63 | 123 | 141 | 167 | 226 |
| 47 | 45 | 64 | 78 | 142 | 168 | 227 |
| 48 | 46 | 65 | 79 | 143 | 169 | 228 |
| 49 | 47 | 66 | 80 | 144 | 170 | 229 |
| 50 | 1 | 67 | 81 | 145 | 171 | 230 |
| 51 | 2 | 68 | 82 | 146 | 172 | 231 |
| 52 | 3 | 69 | 83 | 147 | 173 | 232 |
| 53 | 4 | 70 | 84 | 148 | 174 | 182 |
| 54 | 5 | 72 | 85 | 149 | 175 | 182 |
| 55 | 6 | 72 | 86 | 150 | 176 | 183 |
| 56 | 7 | 72 | 87 | 151 | 177 | 184 |
| 57 | 8 | 74 | 88 | 124 | 178 | 185 |
| 58 | 9 | 75 | 89 | 125 | 179 | 186 |
| 59 | 10 | 76 | 90 | 126 | 180 | 187 |
| 60 | 11 | 77 | 91 | 127 | 181 | 188 |
| 61 | 12 | 48 | 92 | 128 | 152 | 189 |
| 62 | 13 | 49 | 93 | 129 | 153 | 190 |
| 63 | 14 | 50 | 94 | 130 | 154 | 191 |
| 64 | 15 | 51 | 95 | 131 | 155 | 192 |
| 65 | 16 | 52 | 96 | 132 | 156 | 193 |
| 66 | 17 | 53 | 97 | 133 | 157 | 194 |
| 67 | 18 | 54 | 98 | 134 | 158 | 195 |
| 68 | 19 | 55 | 99 | 135 | 159 | 196 |
| 69 | 20 | 56 | 100 | 136 | 160 | 197 |
| 70 | 21 | 57 | 101 | 137 | 161 | 198 |
| 71 | 22 | 58 | 102 | 138 | 162 | 199 |
| 72 | 23 | 59 | 103 | 139 | 163 | 200 |
| 73 | 24 | 60 | 104 | 140 | 164 | 101 |
| 74 | 25 | 61 | 105 | 141 | 165 | 202 |
| 75 | 26 | 62 | 106 | 142 | 166 | 203 |
| 76 | 27 | 63 | 107 | 143 | 167 | 204 |
| 77 | 28 | 64 | 108 | 144 | 168 | 205 |
| 78 | 29 | 65 | 109 | 145 | 169 | 206 |
| 79 | 30 | 66 | 110 | 146 | 170 | 207 |
| 80 | 31 | 67 | 111 | 147 | 171 | 208 |
| 81 | 32 | 68 | 112 | 148 | 172 | 209 |
| 82 | 33 | 69 | 113 | 149 | 173 | 210 |
| 83 | 34 | 70 | 114 | 150 | 174 | 211 |
| 84 | 35 | 72 | 115 | 151 | 175 | 212 |
| 85 | 36 | 72 | 116 | 124 | 176 | 213 |
| 86 | 37 | 72 | 117 | 125 | 177 | 214 |
| 87 | 38 | 74 | 118 | 126 | 178 | 215 |
| 88 | 39 | 75 | 119 | 127 | 179 | 216 |
| 89 | 40 | 76 | 120 | 128 | 180 | 217 |
| 90 | 41 | 77 | 121 | 129 | 181 | 218 |
| 91 | 42 | 48 | 122 | 130 | 152 | 219 |
| 92 | 43 | 49 | 123 | 131 | 153 | 220 |
| 93 | 44 | 50 | 78 | 132 | 154 | 221 |
| 94 | 45 | 51 | 79 | 133 | 155 | 222 |
| 95 | 46 | 52 | 80 | 134 | 156 | 223 |
| 96 | 47 | 53 | 81 | 135 | 157 | 224 |
| 97 | 1 | 54 | 82 | 136 | 158 | 225 |
| 98 | 2 | 55 | 83 | 137 | 159 | 226 |
| 99 | 3 | 56 | 84 | 138 | 160 | 227 |
| 100 | 4 | 57 | 85 | 139 | 161 | 228 |
1. Материальная точка совершает гармонические колебания с периодом Т и амплитудой А. Когда смещение точки равно х1, то скорость ее равна v1, а при смещении х2 скорость ее равна v2. Смещение и скорость определяются по абсолютной величине. Определить смещение х1,если Т=1,1 с; v1=6,8 см/с; х2=2,3 см; v2=4,4 см/с.
2. Материальная точка совершает гармонические колебания с периодом Т и амплитудой А. Когда смещение точки равно х1, то скорость ее равна v1, а при смещении х2 скорость ее равна v2. Смещение и скорость определяются по абсолютной величине. Определить амплитуду А, если х1=11,2 см; v1=4,3 см/с; х2=8,7 см; v2=6,9 см/с.
3. Точка совершает гармонические колебания, уравнение которых имеет вид х=5sin2t. В момент, когда на точку действовала возвращающая сила F=5.10 -3 Н, точка обладала потенциальной энергией 10 -4 Дж. Найти этот момент времени t и соответствующую ему фазу колебания j.
4. Точка участвует одновременно в двух колебаниях одного направления, которые происходят по законам х1=a*coswt и х2=a.cos2ωt. Найти максимальную скорость точки.
5. Стакан массой m1=20 г и площадью поперечного сечения S=5см2 содержит m2=80г ртути и плавает на поверхности воды. Под действием вертикальной силы система выводится из положения равновесия и отпускается. Определите период колебаний системы.
6. Поршень массой m делит цилиндр с газом на две равные части. Допустим, что поршень сдвинули влево на расстояние x и отпустили. Полагая, что процесс изотермический, определить частоту колебаний поршня.
7. Материальная точка совершает колебания по закону х = хоsin(2 p t+ p /6). В какой момент времени ее потенциальная энергия равна кинетической?
8. Тело массой m совершает колебания по закону х=хоsinωt. Определить силу, действующую на тело, и его максимальную кинетическую энергию.
9. Тело движется под действием силы F=Fo·cos(ωt)по закону х=C·sin(ωt). Найти работу силы за время от t=tн до t=tк. Найти работу силы за один период действия и среднюю мощность за тот же период.
10. Материальная точка массой m=50 г совершает гармонические колебания согласно уравнению х=0,1соs3π/2*t м. Определить: 1) возвращающую силу F для момента времени t=0,5 с; 2) полную энергию Е точки.
11. Материальная точка массой m=20 г совершает гармонические колебания по закону х=0,1соs(4π t+ π/4) м. Определить полную энергию Е этой точки.
12. Найти отношение кинетической энергии Wк точки, совершающей гармоническое колебание, к ее потенциальной энергии Wп для моментов, когда смещение точки от положения равновесия составляет: а) х=А/4, б) х=А/2, в) х=А, где А - амплитуда колебаний.
13. Математический маятник массой m=0,10 кг и длиной l=10 м совершает гармонические колебания по закону α = 0,25*sin2pt. Определить натяжение в момент времени t=Т/2.
14. Найти зависимость от времени угла отклонения математического маятника длины 80 см, если в начальный момент маятник находился в состоянии равновесия и его нижнему концу сообщили горизонтальную скорость 0,22 м/с.
15. Тонкий однородный стержень длиной l=60 см может свободно вращаться вокруг горизонтальной оси, проходящей через верхний конец стержня. Стержень отклонили на угол Ао= 0,01 рад и в момент времени tо = 0 отпустили. Считая колебания малыми, определить период колебаний стержня и записать функцию А(t).
16. Физический маятник совершает колебания около горизонтальной оси с периодом Т1. Если к нему прикрепить небольшой груз массы m на расстоянии l ниже оси, то период колебаний будет равен Т2.Момент инерции маятника относительно оси равен J. Определить расстояние l,если Т1 = 1,75с; m=0,85 кг; Т2=2,05 с; J=620 кг.см2.
17. Физический маятник совершает колебания около горизонтальной оси с периодом Т1. Если к нему прикрепить небольшой груз массы m на расстоянии l ниже оси, то период колебаний будет равен Т2. Момент инерции маятника относительно оси равен J. Определить момент инерции J, если Т1=0,68 с; m=0,25 кг; l=25 см; Т2=0,83 с.
18. К концам однородного стержня массой m и длиной l прикреплены небольшие шарики массами m1 и m2 (m1>m2). Период малых колебаний системы относительно горизонтальной оси, проходящей перпендикулярно к стержню через его середину, равен Т. Определить массу m1, если m=25 г; l=37 см; m2=12 г; Т=1,5 с.
19. К концам однородного стержня массой m и длиной l прикреплены небольшие шарики массами m1 и m2 (m1>m2). Период малых колебаний системы относительно горизонтальной оси, проходящей перпендикулярно к стержню через его середину, равен Т. Определить период Т,если m=72 г; l=45 см; m1=130 г; m2=115 г
20. К концам однородного стержня массой m и длиной l прикреплены небольшие шарики массами m1 и m2 (m1>m2). Период малых колебаний системы относительно горизонтальной оси, проходящей перпендикулярно к стержню через его середину, равен Т. Определить длину l, если m=140 г; m1=75 г; m2=35 г; Т=2,4 с.
21. Стержень длиной l= 50 см совершает колебания около горизонтальной оси, проходящей через точку, которая расположена на расстоянии d=12,5 см от конца стержня. Определите частоту колебаний стержня.
22. Амплитуда колебаний математического маятника длиной l за время t1 уменьшается в к1 раз, а за время t2 - в к2 раз. Логарифмический декремент затухания колебаний маятника равен δ. Определить декремент затухания б, если l=45 см; t1=120 с; к1=2,5.
23. Амплитуда колебаний математического маятника длиной l за время t1 уменьшается в к1 раз, а за время t2 - в к2 раз. Логарифмический декремент затухания колебаний маятника равен δ. Определить к2, если t1=370 с; t2=610 с; к1=1,5.
24. За время t полная механическая энергия математического маятника длины l уменьшилась в к раз. Период собственных колебаний маятника равен Т, логарифмический декремент затухания δ. Определить к, если t=75 с; l=0,85 м; δ=0,011.
25. За время t полная механическая энергия математического маятника длины l уменьшилась в к раз. Период собственных колебаний маятника равен Т, логарифмический декремент затухания δ. Определить логарифмический декремент затухания , если t=140 с; к=2,0; Т=0,75 с.
26. Начальная амплитуда колебаний механического маятника А1=0,20 м. Амплитуда после 10 полных колебаний А10=0,01 м. Определить декремент затухания и коэффициент затухания, если период колебаний Т=5 с. Записать уравнение колебаний.
27. К невесомой пружине подвесили грузик, в результате чего она растянулась на 9,8 см. С каким периодом будет колебаться грузи к, если ему дать небольшой толчок в вертикальном направлении? Логарифмический декремент затухания δ=3,1.
28. Колебательный контур состоит из конденсатора емкостью С и катушки с индуктивностью L и сопротивлением R. Добротность контура равна Q. Контур настроен на длину волны λ. Определить длину волны λ, если L=38 мкГ; R=5,3 Ом; Q=110.
29. Колебательный контур состоит из конденсатора емкостью С и катушки с индуктивностью L и сопротивлением R. Добротность контура равна Q. Контур настроен на длину волны λ. Определить добротность контура Q, если С=68 пФ; R=1,2 Ом; λ =27 м.
30. Колебательный контур состоит из конденсатора емкостью С и катушки с индуктивностью L и сопротивлением R. Добротность контура равна Q. Контур настроен на длину волны λ . Определить сопротивление R, если С=810 пФ; Q=95; λ=170м.
31. Колебательный контур содержит конденсатор емкостью С=0,5 нФ и катушку индуктивностью L=0,4 мГн. Определить длину волны излучения, генерируемого контуром.
32. Определить длину электромагнитной волны в вакууме, на которую настроен колебательный контур, если максимальный заряд на обкладках конденсатора Q=50 нКл, а максимальная сила тока в контуре I=1,5 А. Активным сопротивлением контура пренебречь.
33. На какой диапазон волн можно настроить колебательный контур, если его индуктивность равна 2.10-3 Гн, а емкость может меняться от 62 до 480 см? Сопротивление контура ничтожно мало.
34. На струне длиной 120 см образовалась стоячая волна, причем точки струны, для которых амплитуда смещения равна 3,5 мм, отстоят друг от друга на 15,0 см. Найти максимальную амплитуду смещения.
35. Для определения скорости звука в воздухе методом акустического резонанса используется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов. Найти скорость звука, если расстояние между соседними положениями поршня, при которых наблюдается резонанс на частоте 2000 Гц, составляет l=8,5 см.
36. Чему равна скорость распространения звуковой волны в медной проволоке длиной 10 м, которая натянута с силой 200 Н? Масса проволоки 50 г.
37. Чему равен коэффициент всестороннего сжатия воды, если посланный с корабля ультразвуковой сигнал, отразившись на глубине h = 1,5 км, вернулся через t = 2,1 с? Плотность морской воды r =1,03 т/м3.
38. Неподвижный приемник при приближении источника звука, излучающего волны с частотой v0 = 360 Гц, регистрирует звуковые колебания с частотой v=400 Гц. Принимая температуру воздуха Т=290 К, его молярную массу М=29г/моль, определите скорость движения источника звука.
39. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Интенсивность волны, т.е. средняя энергия, проходящая через единицу поверхности за единицу времени, составляет 21,2 мкВт/м2. Определить амплитуду напряженности электрического поля волны.
40. За сколько времени звуковые колебания пройдут расстояние l между точками А и В, если температура воздуха между ними меняется линейно от Т1 до Т2? Скорость звука в газе v = a.T, где а - постоянная.
41. Скорость звука в газе при температуре Т=293 К равна v=343 м/с. Определить отношение теплоемкостей газа, если его молекулярная масса равна 29 г/моль.
42. Плотность некоторого двухатомного газа при нормальном давлении равна 1,78 кг/м3. Определить скорость распространения звука в газе при этих условиях.
43. При повышении температуры от 20 до 100 оС скорость продольных волн в медном стержне убывает на 7,4% скорости при 20 оС. Каков средний температурный коэффициент модуля упругости в этом интервале температур?
44. При помощи эхолота измерялась глубина моря. Какова была глубина моря, если промежуток времени между возникновением звука и его приемом был равен 2,5 с? Коэффициент сжатия воды 4,6.10-10 м2/Н и плотность морской воды 1030 кг/м3.
45. Во сколько раз скорость распространения звука в воздухе летом (температура +27 оС) больше скорости распространения звука зимой (температура -33 оС)?
46. Наблюдатель, находящийся на расстоянии l=800 м от источника звука, слышит звук, пришедший по воздуху на 1,78 с позднее, чем звук, пришедший по воде. Найти скорость v звука в воде, если температура Т воздуха равна 350 К.
47. Скорость v звука в некотором газе при нормальных условиях равна 308 м/с. Плотность газа равна 1,78 кг/м3. Определить отношение Ср/Сv для данного газа.
48. На мыльную пленку (n=1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны 0,55 мкм окажется максимально усиленным в результате интерференции?
49. На тонкий стеклянный клин (n=1,55 ) падает нормально монохроматический свет. Двугранный угол а между поверхностями клина равен 2'. Определить длину световой волны , если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,3 мм.
50. Поверхности стеклянного клина образуют между собой угол Q= 0,2'. На клин нормально к его поверхности падает пучoк лучей монохроматического света с длиной волны λ = 0,55 мкм. Определить ширину интерференционной полосы.
51. Плосковыпуклая линза (n=1,6) выпуклой стороной прижата к стеклянной пластинке. Расстояние между первыми двумя кольцами Ньютона, наблюдаемыми в отраженном свете, равно 0,5 мм. Определить оптическую силу линзы, если освещение производится монохроматическим светом с λ = 550 нм, падающим нормально.
52. Две плосковыпуклые линзы с радиусами кривизны R1 и R2 сложены выпуклыми поверхностями. Радиус m-го светлого интерференционного кольца, наблюдаемого в отраженном свете, равен rm для длины волны λ. Определить радиус rm, если R1=1,4 м; R2=2,7 м; λ=0,59 мкм; m=11.
53. Кольца Ньютона в отраженном свете наблюдаются с помощью плосковыпуклой линзы с радиусом кривизны R1, положенной на вогнутую сферическую поверхность с радиусом кривизны R2. Длина волны света равна λ, радиус m-го темного кольца rm. Определить радиус rm, если R1=1,1 м; R2=3,2 м; λ=0,55 мкм; m=5.
54. Кольца Ньютона в отраженном свете наблюдаются с помощью плосковыпуклой линзы с радиусом кривизны R1, положенной на вогнутую сферическую поверхность с радиусом кривизны R2. Длина волны света равна λ , радиус m=го темного кольца rm. Определить радиус rm, если R1=1,4 м; R2=2,3 м; λ=0,59 мкм; m=12.
55. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна х при длине волны света λ. Определить радиус r, если b=2,4 м; х=0,95мм; λ =0,63 мкм.
56. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна х при длине волны света λ. Определить ширину зоны х, если r=3,5 мм; b=1,7 м; λ=0,55 мкм.
57. Плоская волна падает на круглый диск радиуса r. Точка наблюдения находится на расстоянии b от диска. Ширина зоны Френеля, непосредственно примыкающей к диску, равна х при длине волны света λ. Определить расстояние b, если r=2,2 мм; х=1,3 мм; λ=0,59 мкм.
58. На диафрагму с круглым отверстием радиусом r = 1 мм падает нормально параллельный пучoк света длиной волны 0,5мкм. На пути лучей, прошедших через отверстие, помещают экран. Определить максимальное расстояние bмах от центра отверстия до экрана, при котором в центре дифракционной картины еще будет наблюдаться темное пятно.
59. Зная формулу радиуса k-й зоны Френеля для сферической волны , вывести соответствующую формулу для плоской волны.
60. Радиус 4 четвертой зоны Френеля для плоского волнового фронта равен 3 мм. Определить радиус 6 шестой зоны Френеля.
61. Плоская световая волна (λ=0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром d = 1 см. На каком расстоянии b от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля? 2) две зоны Френеля?
62. На щель шириной а=0,05 мм падает нормально монохроматический свет (λ=0,6мкм).Определить угол между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу.
63. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с 24000Ǻ на 8000Ǻ. Как и во сколько раз изменились энергетическая светимость тела и максимальное значение спектральной плотности энергетической светимости?
64. Температура абсолютно черного тела равна 2000К. Определить: а) спектральную плотность энергетической светимости для длины волны 6000Ǻ; б) энергетическую светимость в интервале длин волн от 5900Ǻ до 6100Ǻ. Принять, что среднее значение спектральной плотности энергетической светимости тела в этом интервале равно значению, найденному для длины волны 6000Ǻ.
65. Энергия, излучаемая через смотровое окошко печи за время t, равна W. Площадь окошка равна S, максимум в спектре излучения приходится на длину волны λ. Определить энергию W, если t=5с; S=5,5см2; λ=1,6мкм.
66. Модель абсолютно черного тела - полость с малым круглым отверстием диаметром d. Нагрев производится электрической спиралью, потребляющей ток I при напряжении U, причем некоторая доля энергии р рассеивается стенками полости. Равновесная температура излучения, исходящего из отверстия, равна T. Определить энергию p, если d=1,5см; I=35мА; U=220В; T=870К.
67. Небольшая болванка с поверхностью S находится в печи с температурой стенок t1. При температуре болванки t2 результирующая энергия, получаемая ею в результате теплообмена излучением со стенками за единицу времени, равна W. Болванку можно считать серым телом с поглощательной способностью a. Определить энергию W, если S=150см2; t1=1100ºС; t2=380ºС; a=0,8
68. Температура поверхности котла равна t1, температура окружающей среды t2. Результирующая энергия, теряемая поверхностью котла в единицу времени за счет теплообмена излучением с окружающей средой, равна W. Величина поверхности котла S, коэффициент поглощения поверхности котла a. Определить коэффициент поглощения a, если t1=+157ºС; t2=-13ºС; S=2,5м2; W=1,47 кВт.
69. Найти с помощью формулы Планка мощность излучения единицы поверхности абсолютно черного тела, приходящегося на узкий интервал длин волн ∆λ=1,0 Нм вблизи максимума спектральной плотности излучения, при температуре тела T=300К.
70. Котел с водой при 97ºС излучает энергию на руку наблюдателя, на поверхности которой температура 27ºС. Во сколько раз больше получит кусок льда такой же поверхности на том же расстоянии? Излучение считать близким к излучению абсолютно черного тела.
71. Какое количество энергии излучает в течение суток каменное оштукатуренное здание общей поверхностью 1000м2, если коэффициент поглощения (поглощательная способность) при этом 0,8 и температура излучающей поверхности 0ºС.
72. Стальная болванка, температура которой 727ºС, излучает за 1с 4Дж энергии с поверхности 1см2. Определить коэффициент поглощения (поглощательную способность) болванки при данной температуре, считая, что он одинаков для всех волн.
73. Звезда с температурой поверхности Т имеет радиус Rз=kRc, где Rc - радиус Солнца. На расстоянии R=nRo от звезды, где Ro - радиус земной орбиты, через перпендикулярную лучам площадку S проходит поток энергии Ф. Можно считать, что звезда излучает как абсолютно черное тело. Определить температуру T, если k=Rз/Rc=530; n=R/Ro=12; S=3,9см2; Ф=42Вт41.
74. 1) Найти насколько уменьшится масса Солнца за год вследствие излучения? 2) Считая излучение Солнца постоянным, найти за какое время масса Солнца уменьшится вдвое. Температуру поверхности Солнца принять равной 5800К.
75. Какую мощность надо подводить к зачерненному металлическому шарику радиусом 2см, чтобы поддерживать его температуру на 27º выше температуры окружающей среды? Температура окружающей среды равна 20ºС. Считать, что тепло теряется только вследствие излучения.
76. Поверхность тела нагрета до температуры 1000К. Затем одна половина этой поверхности нагревается на 100º, другая охлаждается на 100º Во сколько раз изменится энергетическая светимость поверхности этого тела?
77. Температура абсолютно черного тела изменилась при нагревании от 1000К до 3000К. 1) Во сколько раз увеличилась при этом его энергетическая светимость? 2) На сколько изменилась при этом длина волны, на которую приходится максимум спектральной плотности энергетической светимости? 3) Во сколько раз увеличилась его максимальная спектральная плотность энергетической светимости?
78. Поток монохроматического излучения (λ=500нм) падает нормально на плоскую зеркальную поверхность и давит на нее с силой 10-8Н. Определить число фотонов, ежесекундно падающих на эту поверхность.
79. Параллельный пучок монохроматических лучей (λ=662нм) падает на зачерненную поверхность и производит на нее давление 3×10-7Н/м2. Определить концентрацию фотонов в световом пучке.
80. Длина волны λ фотона равна комптоновской длине волны электрона. Определить энергию ε и импульс р фотона.
81. Во сколько раз энергия фотона (λ=550 нм) больше средней кинетической энергии поступательного движения молекулы кислорода при комнатной температуре (17ºС)?
82. Определить поверхностную плотность  потока энергии излучения, падающего на зеркальную поверхность, если световое давление p при перпендикулярном падении лучей равно 10мкПа.
потока энергии излучения, падающего на зеркальную поверхность, если световое давление p при перпендикулярном падении лучей равно 10мкПа.
83. Поток энергии Фе, излучаемый электрической лампой, равен 600 Вт. На расстоянии 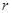 = 1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром
= 1 м от лампы перпендикулярно падающим лучам расположено круглое плоское зеркальце диаметром 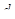 = 2 см. Принимая, что излучение лампы одинаково во всех направлениях и что зеркальце полностью отражает падающий на него свет, определить силу F светового давления на зеркальце.
= 2 см. Принимая, что излучение лампы одинаково во всех направлениях и что зеркальце полностью отражает падающий на него свет, определить силу F светового давления на зеркальце.
84. На зеркальце с идеально отражающей поверхностью площадью  = 1,5 см2 падает нормально свет от электрической дуги. Определить импульс
= 1,5 см2 падает нормально свет от электрической дуги. Определить импульс 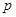 , полученный зеркальцем, если поверхностная плотность потока излучения φ, падающего на зеркальце, равна 0,1МВт/м2. Продолжительность облучения
, полученный зеркальцем, если поверхностная плотность потока излучения φ, падающего на зеркальце, равна 0,1МВт/м2. Продолжительность облучения 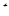 = 1с.
= 1с.
85.Определить энергию  и импульс
и импульс 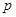 фотона. Которому соответствует длина волны
фотона. Которому соответствует длина волны  нм (фиолетовая граница видимого спектра).
нм (фиолетовая граница видимого спектра).
86. Определить длину волны l и импульс 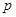 фотона с энергией e = 1МэВ.
фотона с энергией e = 1МэВ.
87. Давление 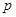 монохроматического света (l = 600 нм ) на черную поверхность, расположенную перпендикулярно падающим лучам, равно 0,1мкПа. Определить число
монохроматического света (l = 600 нм ) на черную поверхность, расположенную перпендикулярно падающим лучам, равно 0,1мкПа. Определить число  фотонов, падающих за время
фотонов, падающих за время  = 1 с на поверхность площадью
= 1 с на поверхность площадью  = 1 см2.
= 1 см2.
88. Монохроматическое излучение с длиной волны l = 500 нм падает нормально на плоскую зеркальную поверхность и давит на нее с силой  = 10нН. Определить число
= 10нН. Определить число  фотонов, ежесекундно падающих на эту поверхность.
фотонов, ежесекундно падающих на эту поверхность.
89. Параллельный пучок монохроматического света (l = 662 нм ) падает на зачерненную поверхность и производит на нее давление p= 0,3мкПа. Определить концентрацию n фотонов в световом пучке.
90. Определить давление солнечных лучей нормально падающих на зеркальную поверхность. Интенсивность солнечного излучения принять равной 1,37 кВт/м2.
91. Плотность потока энергии в импульсе излучения лазера может достигать значения 1,30 . 1020 Вт/м2. Определить давление такого излучения, нормально падающего на черную поверхность.
92. Свет с длиной волны  0,5 мкм нормально падает на зеркальную поверхность и производит на нее давление
0,5 мкм нормально падает на зеркальную поверхность и производит на нее давление  4мкПа. Определить число фотонов, ежесекундно падающих на 1 см2 этой поверхности.
4мкПа. Определить число фотонов, ежесекундно падающих на 1 см2 этой поверхности.
93. На платиновую пластинку падают ультрафиолетовые лучи. Для прекращения фотоэффекта нужно приложить задерживающую разность потенциалов 3,7В. Если платиновую пластинку заменить пластинкой из другого металла, то задерживающую разность потенциалов нужно увеличить до 6В. Определить работу выхода электронов с поверхности этой пластинки.
94. На цинковую пластинку падает монохроматический свет длиной волны 2200Ǻ. Определить максимальную скорость фотоэлектронов.
95. Красная граница фотоэффекта для металла с работой выхода А соответствует длине волны λо. При освещении поверхности металла излучением с длиной волны λ максимальная скорость фотоэлектронов равна u. Определить работу А, если λ=0,14мкм; u=1300км/с.
96. При поочередном освещении поверхности некоторого металла светом с длинами волн λ1=0,35мкм и λ2=0,54мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в n=2,0 раза. Найти работу выхода с поверхности этого металла.
97. Красная граница фотоэффекта рубидия 810нм. Какую обратную разность потенциалов нужно приложить к фотоэлементу, чтобы задержать электроны, испускаемые рубидием под действием ультрафиолетовых лучей с длиной волны 100нм?
98. При падении излучения с длиной волны λ на пластинку из металла с красной границей фотоэффекта λ1, задерживающее напряжение для фотоэлектронов равнялось U1, а при падении на пластинку с красной границей  2 оно равнялось U2.Определить U2, если λ1=0,35мкм; U1=1,4В; λ2=0,45мкм.
2 оно равнялось U2.Определить U2, если λ1=0,35мкм; U1=1,4В; λ2=0,45мкм.
99. При освещении фотокатода площади S излучением с длиной волны λ и плотностью потока энергии Ф ток насыщения в фотоэлементе равен I. Доля фотонов, выбивающих из фотокатода электроны, равна n. Определить n, если λ=0,43мкм; Ф=75эрг/(с×см2); S=1,5см2; I=0,15мкА.
100. На поверхность фотокатода падает поток энергии электромагнитного излучения Ф. Длина волны падающего излучения λ. Определенная доля n фотонов выбивает электроны из фотокатода. Ток насыщения равен I. Определить I, если Ф=55эрг/с; λ=0,36мкм; n=0,05.
101. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян на угол, равный 180º
102. Фотон с энергией 0,25МэВ рассеялся на свободном электроне. Энергия рассеянного фотона 0,2МэВ. Определить угол рассеяния.
103. Фотон с энергией 1,00МэВ рассеялся на свободном покоившемся электроне. Найти кинетическую энергию электрона отдачи, если в результате рассеяния длина волны фотона изменилась на 25%.
104. Рентгеновский фотон испытал комптоновское рассеяние на угол J. Первоначальная энергия фотона W1, энергия после рассеяния W2, энергия электрона отдачи We. Определить W2, (МэВ). Если J=48°; W1=0,15МэВ.
105. При рассеянии рентгеновского излучения с длиной волны λ на угол J кинетическая энергия отдачи равна We, угол между падающим фотоном и направлением движения электрона отдачи равен g. Определить We (кэВ). Если λ=3,2пм; g=22º.
106. При рассеянии рентгеновского излучения с длиной волны λ на угол J кинетическая энергия электрона отдачи равна We, угол между падающим фотоном и направлением движения электрона отдачи равен g. Определить λ (пм). Если J=130º; We=85кэВ.
107. Определить наименьшее и наибольшее значения энергии фотона в ультрафиолетовой серии спектра водорода (серии Лаймана).
108. Фотон с энергией 16,5эВ выбил электрон из невозбужденного атома водорода. Какую скорость будет иметь электрон вдали от ядра атома?
109. Электрон движется по второй орбите атома водорода. Найти длину волны де Бройля.
110. Атомарный водород переведен из нормального состояния в возбужденное, характеризуемое главным квантовым числом 3. Какие спектральные линии могут появиться в спектре водорода при переходе атома из возбужденного состояния в нормальное?
111. Атом водорода в основном состоянии поглотил квант света с энергией 12,09эВ. Определить кинетическую, потенциальную и полную энергию электрона в возбужденном атоме.
112. Насколько изменится орбитальный момент импульса электрона в атоме водорода (момент количества движения) при испускании атомом второй по порядку спектральной линии серии Бальмера (электрон переходит с 4-го уровня на 2-ой)?
113. На каком энергетическом уровне находятся возбужденные атомы водорода, если они испускают только три спектральных линии? Определить энергию возбуждения атомов водорода и наименьшую длину волны в спектре испускания. Решение пояснить схемой энергетических уровней с обозначением переходов электрона.
114. Возбужденный атом водорода при переходе в основное состояние испустил последовательно только два кванта с длинами волн 1281,8нм и 102,57нм. Вычислить энергию первоначального состояния данного атома и соответствующее ему квантовое число.
115. Определить потенциальную П, кинетическую Т и полную энергии электрона, находящегося на первой орбите атома водорода.
116. Найти наибольшую lmax и наименьшую lmin длины волн в первой инфракрасной серии спектра водорода (серии Пашена).
117. Найти энергию 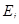 и потенциал
и потенциал 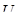 ионизации ионов
ионизации ионов 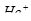 и
и 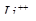
118. Вычислить частоты n1 и n2 вращения электрона в атоме водорода на второй и третьей орбитах. Сравнить эти частоты с частотой n излучения при переходе электрона с третьей на вторую орбиту.
119. Атом водорода в основном состоянии поглотил квант света с длиной волны l = 121,5 нм. Определить радиус 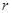 электронной орбиты возбужденного атома водорода.
электронной орбиты возбужденного атома водорода.
120. Определить первый потенциал 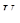 возбуждения атома водорода.
возбуждения атома водорода.
121. Вычислить длину волны l которую испускает ион гелия 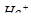 при переходе со второго энергетического уровня на первый. Сделать такой же подсчет для иона лития
при переходе со второго энергетического уровня на первый. Сделать такой же подсчет для иона лития 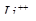
122. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию Тmin электрона, движущегося внутри сферической области диаметром d=0,1нм.
123. Атом испустил фотон с длиной волны λ=600нм. Продолжительность излучения t=50нс. Определить наибольшую точность (Dλ), с которой может быть измерена длина волны излучения.
124. Определить неточность Dх в определении координаты электрона, движущегося в атоме водорода со скоростью v=1.5×106м/с, если допускаемая неточность Dv в определении скорости составляет 10% от ее величины. Сравнить полученную неточность с диаметром d водорода, вычисленным по теории Бора для основного состояния, и указать, применимо ли понятие траектории в данном случае.
125. Электрон с кинетической энергией T=15эВ находится в металлической пылинке диаметром d=1мкм. Оценить (в процентах) относительную неточность, с которой может быть определена скорость электрона.
126. Во сколько раз дебройлевская длина волны λ частицы меньше неопределенности ее координаты Dх, которая соответствует неопределенности ее импульса в 1%.
127. Используя соотношение неопределенности DхDр³ħ, оценить низший энергетический уровень электрона в атоме водорода. Принять линейные размеры атома 1А.
128. Приняв, что минимальная энергия нуклона в ядре Еmin=10МэВ, оценить исходя из соотношения неопределенности, размеры ядра.
129. Оценить наименьшие ошибки, с которыми можно определить скорость электрона, протона и шарика массой 1мг, если координаты частиц и центра шарика установлены с неопределенностью 1мкм.
130. Оценить с помощью соотношения неопределенностей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.
131. Ширина следа электрона от фотографии, полученной с помощью камеры Вильсона составляет Dх = 10-3м. Найти неопределенность в определении скорости.
132. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна ℓ. Оценить с помощью соотношения неопределенностей силу давления электрона на стенки этой ямы при минимально возможной его энергии.
133. Пучок электронов с кинетической энергией W попадает в ускоряющее электрическое поле напряженностью Е. После того, как электроны прошли вдоль силовых линий поля расстояние ℓ, их дебройлевская длина волны стала равной λ. Определить напряженность Е, если W=0,35МэВ; ℓ=25см; λ=1,2пм.
134. Атом испустил фотон с длиной волны λ=600нм. Продолжительность излучения t=50нс. Определить наибольшую точность (Dλ), с которой может быть измерена длина волны излучения.
135. Частица с зарядом q=Zе (е - элементарный заряд) и массой M=Аm (m-масса протона), движущегося со скоростью u, попадает в однородное тормозящее электрическое поле с напряженностью Е и проходит вдоль его силовых линий расстояние ℓ. После этого дебройлевская длина волны частицы оказывается равной λ. Определить ℓ, см, если: Z=1; А=1; u=2700км/с; Е=1,2кВ/с; λ=0,28пм.
136. Альфа-частица движется по окружности радиусом r=8.3мм в однородном магнитном поле, напряженность которого Н=18.9кА/м. Найти длину волны де Бройля λ для α-частицы.
137. За один год начальное количество радиоактивного изотопа уменьшилось в три раза. Во сколько раз оно уменьшится за два года?
138. За какое время  распадается
распадается 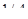 начального количества ядер радиоактивного изотопа, если период его полураспада
начального количества ядер радиоактивного изотопа, если период его полураспада 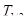 = 24 ч?
= 24 ч?
139. За время  = 8сут распалось
= 8сут распалось  начального количества ядер радиоактивного изотопа. Определить период полураспада
начального количества ядер радиоактивного изотопа. Определить период полураспада 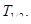
140. При распаде радиоактивного полония 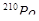 в течение времени
в течение времени  = 1ч образовался гелий
= 1ч образовался гелий 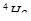 , который при нормальных условиях занял объем
, который при нормальных условиях занял объем 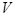 = 89,5 см3. Определить период полураспада
= 89,5 см3. Определить период полураспада 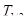 полония.
полония.
141. Период полураспада 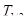 радиоактивного нуклида равен 1 ч. Определить среднюю продолжительность t жизни этого нуклида.
радиоактивного нуклида равен 1 ч. Определить среднюю продолжительность t жизни этого нуклида.
142. Какая часть начального количества радиоактивного нуклида распадается за время  равное средней продолжительности t жизни этого нуклида?
равное средней продолжительности t жизни этого нуклида?
143. Активность A препарата уменьшилась в 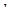 = 250 раз. Скольким периодам полураспада
= 250 раз. Скольким периодам полураспада 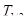 равен протекший промежуток времени
равен протекший промежуток времени  ?
?
144. За время 1 сутки активность изотопа уменьшилась от А1= 118 ГБк до А2=7,4 ГБк. Определить период полураспада Т1/2 этого нуклида.
145. Определить промежуток времени 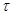 , в течение которого активность А изотопа стронция 90Sr уменьшится в k1=10раз? в k2=100раз?
, в течение которого активность А изотопа стронция 90Sr уменьшится в k1=10раз? в k2=100раз?
146. Определить активность А фосфора 32Р массой m=1мг.
147. Найти отношение массовой активности 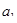 стронция
стронция 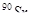 к массовой активности
к массовой активности 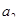 радия
радия 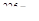 .
.
148. Определить массу  радона
радона  , находящегося в радиоактивном равновесии с радием
, находящегося в радиоактивном равновесии с радием  массой
массой  = 1г.
= 1г.
149. Уран 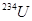 является продуктом распада наиболее распространенного изотопа урана
является продуктом распада наиболее распространенного изотопа урана 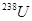 . Определить период полураспада T1/2 урана
. Определить период полураспада T1/2 урана 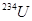 , если его массовая доля w в естественном уране
, если его массовая доля w в естественном уране 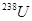 равна 6 . 10-5 .
равна 6 . 10-5 .
150. Радиоактивный изотоп 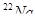 излучает g- кванты энергией e = 1,28МэВ. Определить мощность
излучает g- кванты энергией e = 1,28МэВ. Определить мощность 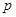 гамма-излучения и энергию
гамма-излучения и энергию 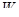 , излучаемую за время
, излучаемую за время  = 5 мин изотопом натрия массой
= 5 мин изотопом натрия массой  = 5 г. Считать, что при каждом акте распада излучается один g - фотон с указанной энергией.
= 5 г. Считать, что при каждом акте распада излучается один g - фотон с указанной энергией.
151. Определить интенсивность 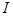 гамма-излучения на расстоянии
гамма-излучения на расстоянии 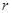 = 5 см от точечного изотропного радиоактивного источника, имеющего активность
= 5 см от точечного изотропного радиоактивного источника, имеющего активность 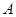 = 148ГБк. Считать, что при каждом акте распада излучается в среднем
= 148ГБк. Считать, что при каждом акте распада излучается в среднем 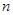 = 1,8 g - фотонов с энергией e = 0,5МэВ каждый.
= 1,8 g - фотонов с энергией e = 0,5МэВ каждый.
152. В баллоне, объем которого 0,250м3 , находится газ, состоящий из смеси углекислого газа и паров воды. Температура газа 327оС. Число молекул углекислого газа N1=6,60·1021, число молекул паров воды N2=0,90·1021. Вычислить давление р и молекулярный вес m газовой смеси.
153. Плотность газа, состоящего из смеси гелия и аргона при давлении 1,50 атм и температуре 27оС, равна ρ=2,00г/л. Сколько атомов гелия содержится в 1см3 газовой смеси?
154. Найти отношение средней квадратичной скорости молекул газа к скорости распространения звука в идеальном газе при той же температуре. Газ состоит из одноатомных молекул.
155. Найти энергию Е теплового движения молекул NH3, находящихся в баллоне объемом 10,0л, при давлении 18,4 мм.рт.ст. Какую часть этой энергии составляет энергия поступательного движения молекул Е? Молекулы считать жесткими.
156. Теплоизолированный сосуд с азотом движется со скоростью V=86,0м/с. Температура газа 0оС. Какова будет средняя энергия поступательного движения молекул газа, если сосуд остановить?
157. В баллоне, объем которого V=2,55л, находится m=1,50·10-2г водорода при температуре 2500оС. При этой температуре молекулы водорода оказываются упругими, причем часть молекул диссоциирует на атомы. Степень диссоциации молекул a=0,25. Вычислить давление р и количество тепла DQ, необходимое для нагревания водорода на 1оС при указанных условиях.
158. Средняя квадратичная скорость некоторого газа при нормальных условиях равна 480м/с. Сколько молекул содержит 1г этого газа?
159. В сосуде вместимостью V=0,3л при температуре Т=290К находится некоторый газ. Насколько понизится давление р в сосуде, если из него из-за утечки выйдет N=1019молекул?
160. Определить среднюю кинетическую энергию поступательного движения молекулы газа, находящегося под давлением 0,1 Па. Концентрация молекул газа равна 1013см-3.
161. В баллоне вместимостью V=1л находится азот при нормальных условиях. Когда азот нагрели до температуры Т=1,8кК, то молекулы азота оказались частично диссоциированными на атомы. Степень диссоциации а=0,3. Определить количество вещества и концентрацию n атомов атомарного азота после нагревания.
162. Определить среднюю кинетическую энергию поступательного движения и среднее значение полной кинетической энергии молекулы водяного пара при температуре Т=600°К. Найти также кинетическую энергию W поступательного движения всех молекул пара, содержащего количество вещества ν=1кмоль.
163. Для получения высокого вакуума в стеклянном сосуде необходимо прогревать его при откачке с целью удаления адсорбированного газа. Определить, на сколько повысится давление в сферическом сосуде радиусом R=10см, если все адсорбированные молекулы перейдут со стенок в сосуд. Слой молекул на стенках считать мономолекулярным, сечение одной молекулы равно 10-15см2. Температура Т, при которой производится откачка, равна 600°К.
164. Молярная энергия диссоциации 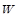 (энергия, затрачиваемая на диссоциацию всех молекул газа, содержащего количество вещества, равное молю) водорода равна 419кДж/моль. При какой температуре Т газа средняя кинетическая энергия поступательного движения его молекул достаточна для их расщепления?
(энергия, затрачиваемая на диссоциацию всех молекул газа, содержащего количество вещества, равное молю) водорода равна 419кДж/моль. При какой температуре Т газа средняя кинетическая энергия поступательного движения его молекул достаточна для их расщепления?
165. При какой температуре Т молекулы кислорода имеют такую же среднюю квадратичную скорость, как молекулы водорода при температуре Т1=100°К?
166. В баллоне объемом V находится смесь кислорода и гелия. Число молекул кислорода равно N1 число молекул гелия - N2. Температура смеси равна Т, давление - р. Среднее значение молекулярной массы смеси равно m. Определить р, если V=0,25м3, N1 =0,6·1021, N2=0,9·1021, Т=620°К.
167. При температуре t давление газа равно р, средняя длина свободного пробега молекул ℓ. Эффективное сечение молекул газа равно s. Определить ℓ, если t=17о С; р=11кПа, s =24·10-20 м2
168. При температуре t и давлении р молекула газа испытывает в единицу времени z соударений с другими молекулами. Масса кило моля газа m, эффективный диаметр молекул d, средняя длина свободного пробега ℓ. Определить t, если р=360мм.рт.ст.; d=0,29нм, ℓ=150нм.
169.Можно ли считать вакуум с давлением р=100мкПа высоким, если он создан в колбе диаметром d=20см, содержащей азот при температуре Т=290°К?
170. Средняя длина свободного пробега <l> атомов гелия при нормальных условиях равна 180нм. Определить коэффициент диффузии D гелия.
171. Диффузия D кислорода при температура t=0оС равна 0,19см2/с. Определить среднюю длину свободного пробега <l> молекул кислорода.
172. Определить, во сколько раз отличается диффузия D1 газообразного водорода от диффузии D2 газообразного кислорода, если оба газа находятся при одинаковых условиях.
173. Вычислить динамическую вязкость кислорода при нормальных условиях.
174. Найти среднюю длину свободного пробега <l> молекул азота при условии, что его динамическая вязкость равна 17мкПа×с.
175. Найти динамическую вязкость гелия при нормальных условиях, если диффузия D при тех же условиях равна 1,06·10-4м2/с.
176. При нормальных условиях динамическая вязкость воздуха равна 17,2мкПа·с. Найти для тех же условий теплопроводность воздуха.
177. Определить коэффициент теплопроводности азота, находящегося в некотором объеме при температуре 280°К. Эффективный диаметр молекул азота принять равным 0,38нм.
178. Кислород находится при нормальных условиях. Определить коэффициент теплопроводности кислорода, если эффективный диаметр его молекул равен 0,36нм.
179. Пространство между двумя параллельными пластинами площадью 150см2 каждая, находящимися на расстоянии 5мм друг от друга, заполнено кислородом. Одна пластина поддерживается при температуре 17°С, другая - при температуре 27°С. Определить количество теплоты, прошедшее за 5мин посредством теплопроводности от одной пластины к другой. Кислород находится при нормальных условиях. Эффективный диаметр молекул кислорода считать равным 0,35нм.
180. Азот находится под давлением 100кПа при температуре 290°К. Определить коэффициенты диффузии D и внутреннего трения. Эффективный диаметр молекул азота принять равным 0,35нм.
181. Толщина деревянной стены 10см. Какой должна быть толщина кирпичной стены, чтобы она обладала такой же теплопроводностью, как деревянная?
182. Определить скорость, соответствующую максимуму функции распределения при 100оС для водорода, гелия и азота.
183. Какая часть молекул воздуха при температуре 17оС обладает скоростями, отличающимися не больше, чем на 0,50м/с от скорости, равной υ=0,1υвер? Молекулярный вес воздуха 29.
184. Найти число молекул гелия в 1см3, скорости которых лежат в интервале от 2,39·103м/с до 2,61·103м/с. Температура гелия 690оС, его плотность 2,16·10-4кг/м3.
185. При каком значении скорости υ пересекаются кривые распределения Максвелла для температур Т1 и Т2=2Т1
186. Найти давление воздуха в шахте на глубине 10км. На поверхности Земли давление 760мм.рт.ст., молекулярный вес воздуха 29. Считать, что температура воздуха не зависит от высоты и равна 0оС.
187. При какой температуре средняя квадратичная скорость молекул кислорода больше их наиболее вероятной скорости на 100м/с?
188. Вычислить массу азота и массу кислорода в 1м3 воздуха на уровне моря и на высоте 5532м. Температура воздуха и его давление на уровне моря равны соответственно 0оС и 1,01·105Н/м2.
189. Вычислить, на какой высоте парциальное давление азота и углекислого газа уменьшаются в два раза, если температура равна 0оС. Какие высоты получаются при 30оС.
190. На какой высоте h над уровнем моря плотность воздуха уменьшается в два раза? Считать, что температура воздуха Т и ускорение силы тяжести g не зависят от h. Молекулярный вес воздуха 29, температура 0°С.
191. На какой высоте h над уровнем моря плотность кислорода уменьшается на 1%? Температура кислорода 27°C.
192. На какой высоте давление воздуха составляет 60% от давления на уровне моря? Считать, что температура воздуха везде одинакова и равна 10оС.
193. Пылинки, взвешенные в воздухе, имеют массу m=10-18г. Во сколько раз уменьшится их концентрация n при увеличении высоты Dh на 10м? Температура воздуха Т=300K.
194. На сколько уменьшится атмосферное давление р=100кПа при подъеме наблюдателя над поверхностью Земли на высоту h=100м? Считать, что температура Т воздуха равна 290К и не изменяется с высотой?
195. Найти изменение высоты Dh, соответствующее изменению давления на Dр=100Па вблизи поверхности Земли, где температура Т=290°К, давление р=100кПа.
196. Барометр в кабине летящего самолета все время показывает одинаковое давление р=80кПа, благодаря чему летчик считает высоту h полета неизменной. Однако температура воздуха изменилась на DТ=1°К. Какую ошибку Dh в определении высоты допустил летчик? Считать, что температура не зависит от высоты и что у поверхности Земли давление ро=100кПа.
197. Вычислить по классической теории теплоемкости теплоемкость С кристалла бромида алюминия объемом 1м3 и плотностью 3010кг/м3.
198. Определить изменение внутренней энергии кристалла никеля при нагревании его от Т1=0˚С до Т2=200˚С. масса кристалла 20г. Теплоемкость вычислить.
199. Определить среднюю энергию линейного одномерного квантового осциллятора при температуре Т=200К.
200. Определить энергию U системы, состоящей из n=1023 независимых квантовых трехмерных осцилляторов, при температуре Т=300˚К.
201. Найти частоту колебаний атомов серебра по теории теплоемкости Эйнштейна, если характеристическая температура серебра равна 165˚К.
202. Используя квантовую теорию теплоемкости Эйнштейна, вычислить изменение DU молярной внутренней энергии кристалла при нагревании его на DТ=2˚К от температуры 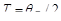 .
.
203. Пользуясь теорией теплоемкости Эйнштейна, определить изменение DU мoлярной внутренней энергии кристалла при нагревании его от нуля до температуры 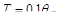 . Характеристическая температура Эйнштейна для данного кристалл равна 300˚К.
. Характеристическая температура Эйнштейна для данного кристалл равна 300˚К.
204. Определить относительную погрешность, которая будет допущена, если при вычислении теплоемкости С вместо значения, даваемого теорией Эйнштейна (при  ), воспользоваться значением , даваемым законом Дюлонга и Пти.
), воспользоваться значением , даваемым законом Дюлонга и Пти.
205. Определить максимальную частоту собственных колебаний в кристалле золота по теории Дебая. Характеристическая температура равна 180˚К.
206. Вычислить максимальную частоту Дебая, если известно, что малярная теплоемкость серебра с = 1.7Дж/(моль К) при Т=20˚К. Считать условие  выполненным.
выполненным.
207. Найти отношение изменения внутренней энергии кристалла DU при его нагревании от нуля до 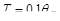 к нулевой энергии U0 . Считать условие
к нулевой энергии U0 . Считать условие 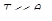 выполненным.
выполненным.
208. Используя квантовую теорию теплоемкости Дебая, вычислить изменение DU молярной внутренней энергии кристалла при нагревании его на DТ=2˚К от температуры 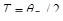 .
.
209. При нагревании серебра массой 10г от Т1=10˚К до Т2=20К было подведено DQ=0.71Дж теплоты. Определить характеристическую температуру Дебая серебра. Считать условие 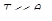 выполненным.
выполненным.
210. Определить относительную погрешность, которая будет допущена, если при вычислении теплоемкости С кристалла вместо значения, даваемого теорией Дебая (при Т=QД), воспользоваться значением , даваемым законом Дюлонга и Пти.
211. Найти отношение характеристических температур Эйнштейна и Дебая.
212.Определить плотность кальция (решетка гранецентрированная кубическая), если расстояние d между ближайшими атомами равно 0.393нм.
213.Стронций имеет гранецентрированную кубическую решетку. Определить расстояние d между ближайшими соседними атомами, если параметр а решетки равен 0.605нм.
214. Определить число Z элементарных ячеек в единице объема кристалла бария (решетка объемно-центрированная кубическая). Плотность бария считать известной.
215. Барий имеет объемно-центрированную кубическую решетку. Плотность кристалла бария считать равной 3.5·103кг/м3. Определить параметр а решетки.
216. Алюминий имеет гранецентрированную кубическую решетку. Параметр а решетки равен 0.404нм. Определить плотность алюминия.
217. Ванадий имеет объемно-центрированную кубическую решетку. Определить расстояние d между ближайшими соседними атомами и параметр а решетки. Плотность ванадия считать известной.
218. Расстояние d между ближайшими соседними атомами кристаллической решетки золота равно 0.288нм. Определить параметр а решетки, если решетка гранецентрированная кубическая.
219. Никель имеет гранецентрированную кубическую решетку. Определить расстояние d между ближайшими соседними атомами и параметр а решетки. Плотность никеля считать известной.
220. Определить число элементарных ячеек кристалла объемом 1м3 хлористого цезия (решетка объемно-центрированная решетка кубической сингонии).
221. Определить число элементарных ячеек кристалла объемом 1м3 меди (гранецентрированная решетка кубической сингонии).
222. Найти плотность кристалла неона (при Т=20К), если известно, что решетка гранецентрированная кубической сингонии. Постоянная а решетки при той же температуре равна 0.452 нм.
223. Найти плотность кристалла стронция, если известно, что решетка гранецентрированная кубической сингонии, а расстояние d между ближайшими соседними атомами равно 0.43нм.
224. Определить относительную атомную массу А кристалла, если известно, что расстояние d между ближайшими соседними атомами равно 0.304нм. Решетка объемно-центрированная кубической сингонии. Плотность кристалла равна 543кг/м3
225. Найти постоянную а решетки и расстояние d между ближайшими соседними атомами кристалла алюминия (решетка гранецентрированная кубической сингонии).
226. Найти постоянную а решетки и расстояние d между ближайшими соседними атомами кристалла вольфрама (решетка объемно-центрированная кубической сингонии).
227. Определить концентрацию n свободных электронов при температуре Т=0˚К. Энергию Ферми принять равной 1 эВ.
228. Определить отношение концентраций n1/n2 свободных электронов при Т=0˚К в литии и цезии, если известно, что уровни Ферми в этих металлах соотв. равны 4.72эВ и 1.53эВ.
229. Определить число свободных электронов, которое приходится на один атом натрия при температуре Т=0˚К. Уровень Ферми для натрия равен 3.12эВ. Плотность натрия равна 970кг/м3.
230. Вычислить среднюю кинетическую энергию электронов в металле при температуре Т=0˚К, если уровень Ферми равен 7эВ.
231. Определить максимальную скорость электронов в металле при T=0˚К, если уровень Ферми равен 5эВ.
232. Определить уровень Ферми в свободном полупроводнике, если энергия активации равна 0.1эВ. За нулевой уровень отсчета кинетической энергии принять низший уровень зоны проводимости.
Содержание
Введение ……………….…………………………….…3
Рабочая программа……………………………..………… 7
Методические материалы к контрольной работы № 2....11
Контрольная работа № 2 ……………..……….………….88
Учебное издание.
Анатолий Алексеевич Босенко,
ФИЗИКА
Контрольные работы № 2.
Физика колебаний и волн.
Квантовая и атомная физика.
Термодинамика и молекулярная физика.
Технический редактор:
Подписано в печать _______________ Формат 60х90 1/16
Бумага для множительной техники
Усл.печ.л.____7.0____ Тираж _____ экз. Заказ _________

Отпечатано с авторского оригинала в центре информационных технологий СОФ МГРИ-РГГРУ
Дата: 2019-02-19, просмотров: 914.