МИНОБРНАУКИ РОССИИ
СТАРООСКОЛЬСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ОБРАЗОВАНИЯ
«Российский государственный геологоразведочный университет имени
Серго Орджоникидзе»
(СОФ МГРИ-РГГРУ)
 |
А.А. Босенко
ФИЗИКА
Контрольные работы № 3,4
Физика колебаний и волн
Квантовая и атомная физика
Термодинамика и молекулярная физика
Учебное пособие
для студентов горно-геологических направлений
Старый Оскол
СОФ МГРИ - РГГРУ
2017 г
УДК 53
ББК 22.3
Рецензент: А.Х. Иванова, доцент, кандидат физико-математических наук ( Старооскольский технологический институт )
Босенко А.А.
Физика. Контрольные работы №2. Физика колебаний и волн. Квантовая и атомная физика. Термодинамика и молекулярная физика./А.А. Босенко – Старый Оскол: СОФ МГРИ - РГГРУ, 2017, – 122 с.
В пособие включены программа учебного курса и все необходимые материалы для самостоятельной работы студентов при изучении курса физики по разделам “ Физика колебаний и волн.” “Квантовая и атомная физика.” “Термодинамика и молекулярная физика.”
Для студентов технических направлений высших учебных заведений
УДК 53
ББК 22.3
© А.А. Босенко 2017 г.
ВВЕДЕНИЕ
Курс общей физики студенты заочного отделения изучают на первом и втором курсах. Занятия по расписанию (аудиторные) проводятся в форме лекций, практических, лабораторных занятий и консультаций.
Контроль знаний осуществляется при защите контрольных работ и отчетов о проделанных лабораторных работах, при сдаче зачетов и экзаменов. Содержание курса изложено в рабочей программе. Рабочая программа курса составлена на основе требований Государственного стандарта и типовой программы по физике, утвержденной Главным учебно-методическим управлением министерства образования.
Пособие содержит основной справочный материал необходимый при выполнении контрольных работ и примеры решения задач по основным темам разделов “Физика колебаний и волн. Квантовая и атомная физика. Молекулярная физика. Термодинамика.” курса физики и задачи контрольных работ.
Контрольные работы.
Контрольные работы позволяют закрепить теоретический материал. В процессе изучения третьей и четвёртой части курса физики студент должен выполнить две контрольные работы. Решение задач контрольных работ является проверкой степени усвоения студентами теоретического курса, а рецензии на работу помогают ему доработать и правильно усвоить различные разделы курса физики. Контрольные работы выполняются в период между сессиями и сдаются для проверки не позднее, чем за 15 дней до начала сессии.
Перед выполнением контрольной работы необходимо внимательно ознакомится с примерами решения задач по данной теме, уравнениями и формулами, а также со справочными материалами. Прежде, чем приступить к решению той или иной задачи, необходимо хорошо понять ее содержание и поставленные вопросы.
Решенные задачи следует оформить так, как указано ниже.
Контрольные работы, оформленные без соблюдения указанных правил, а так же работы, выполненные не по своему варианту, не будут зачтены.
При наличии значительных ошибок и неправильных решений работа возвращается студенту для исправлений. После исправления работа отправляется на кафедру физики на повторное рецензирование. Защита контрольных работ происходит в виде собеседования по решенным задачам на консультациях во время сессии.
Контрольные работы, включенные в данное пособие, распределены следующим образом: № 3 Физика колебаний и волн. № 4 Квантовая и атомная физика. Молекулярная физика. Термодинамика.
Каждая контрольная работа содержат по пять задач.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
КОНТРОЛЬНЫХ РАБОТ:
1) Контрольная работа оформляется в отдельной тетради. Титульный лист оформляется следующим образом:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Старооскольский филиал
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
"Российский государственный геологоразведочный университет имени Серго Орджоникидзе"
(СОФ МГРИ-РГГРУ)
Контрольная работа по физике N ....
“ ..........................................”
(н а з в а н и е к. р.)
студент_______ группы__________
.....................................................
( Ф. И. О. )
вариант N ...... (.................................)
н о м е р а з а д а ч
"Зачтено"
_________ дата _________ роспись преподавателя
Номер варианта соответствует двум последним цифрам номера зачётной книжки.
2) Каждая задача оформляется с начала нового листа. В начале полностью (без сокращений) записывается текст задачи так, как он приведен в методичке.
3) Все, содержащиеся в задаче данные, которые могут быть представлены в виде математических соотношений, должны быть записаны в колонке под заголовком "Дано" (краткое условие).
4) Величины, выраженные через внесистемные единицы, должны быть переведены в единицы системы СИ. Численное значение всех величин должно быть представлено в нормализованном виде: (1-9,99).10n
5) Решению задачи должно предшествовать изображение физических явлений и процессов, происходящих в данной задаче. На рисунке, чертеже или блок-схеме должны быть указаны характерные параметры данной задачи, известные и искомые физические величины.
6) Задачу рекомендуется решить сначала в общем виде, т.е. только в буквенных обозначениях, поясняя при написании формул буквенные обозначения. Решение задачи должно содержать краткие пояснения основных этапов. Значение фундаментальных физических констант, которые используются в данной задаче, должно быть приведено с указанием их численного значения и размерности в системе СИ.
7) Далее необходимо провести проверку размерности полученного выражения. Для этого в конечную формулу для искомой величины необходимо подставить вместо буквенных параметров их размерности в системе СИ. Затем преобразовать эти размерности, используя связи и соотношения между самими величинами в виде физических законов и определяющих формул. Полученная в результате проверки размерность искомой величины должна совпадать с ее размерностью в системе СИ.
8) После проверки размерности в полученную формулу для искомой величины подставить численные значения каждого из параметров задачи и записать ответ.
9) Полученное значение искомой величины должно быть проанализировано с точки зрения вероятности попадания данной величины в интервал ее возможных значений.
Данный перечень требований с необходимостью должен быть применен к каждой из задач!
10) В конце контрольной работы, после решения всех указанных в маршруте номеров задач, необходимо привести список использованной литературы.
Рабочая программа
Тема 3. Физика колебаний и волн.
3.1. Понятие о колебательных процессах. Единый подход к колебаниям различной физической природы. Кинематика гармонических колебаний. Амплитуда, частота, фаза колебаний. Сложение колебаний. Комплексная форма представления колебаний. Векторные диаграммы. Гармонический осциллятор. Маятник, груз на пружине, колебательный контур.
3.2. Свободные затухающие колебания. Коэффициент затухания, логарифмический декремент, добротность. Энергетические соотношения для осциллятора. Вынужденные колебания осциллятора под действием синусоидальной силы. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
3.3. Процесс установления колебаний. Время установления и его связь с добротностью. Параметрический резонанс. Осциллятор как спектральный прибор. Фурье-разложение. Физический смысл спектрального разложения. Модулированные колебания. Ангармонические колебания. Физические системы, содержащие нелинейность.
3.4. Волны. Плоская волна. Бегущая и стоячая волны. Фазовая скорость, длина волны, волновое число. Эффект Доплера. Продольные волны в твердом теле. Энергетические соотношения. Вектор Умова. Упругие волны в газах и жидкостях. Плоские электромагнитные волны. Вектор Пойнтинга.
3.5. Интерференция монохроматических волн. Способы получения когерентных волн и интерференционных картин. Интерферометры.
3.6. Дифракция волн. Принцип Гюйгенса-Френеля. Приближения Френеля. Простые задачи дифракции. Дифракция Фраунгофера. Дифракционная решетка.
3.7. Принцип голографии. Распространение волн в средах с дисперсией. Нормальная и аномальная дисперсия. Поглощение света. Прозрачные среды. Поляризация света. Искусственная анизотропия.
Тема 4. Квантовая физика.
4.1. Противоречия классической физики. Проблемы излучения черного тела, фотоэлектрического эффекта, стабильности и размера атома. Открытие постоянной Планка. Экспериментальное обоснование основных идей квантовой теории. Опыты Франка и Герца, Штерна и Герлаха.
4.2. Правило частот Бора. Линейчатые спектры атомов. Энергия и импульс световых квантов. Фотоэффект. Эффект Комптона. Вынужденное и спонтанное излучение фотонов.
4.3. Корпускулярно-волновой дуализм. Гипотеза де-Бройля. Микрочастица в двухщелевом интерферометре. Соотношения неопределенностей. Оценка основного состояния атома водорода и объяснение устойчивости атома.
4.4. Квантовое состояние. Задание состояния микрочастицы; волновая функция; ее статистический смысл. Суперпозиция состояний в квантовой теории. Амплитуда вероятностей. Объяснение поведения микрочастицы в интерферометре.
4.5. Уравнение Шредингера. Стационарные состояния. Частица в одномерной прямоугольной яме. Прохождение частицы под барьером. Объяснение туннельного эффекта.
4.6. Атом. Частица в сферически симметричном поле. Водородоподобные атомы. Энергетические уровни. Потенциалы возбуждения и ионизации. Принцип Паули. Периодическая система элементов Д.И. Менделеева. Молекула водорода. Физическая природа химической связи.
4.7. Атомное ядро. Строение и феноменологические модели ядра. Ядерные реакции. Радиоактивные превращения атомных ядер. Цепная реакция деления. Проблемы источников энергии. Термоядерные реакции. Энергия звезд.
Тема 5. Термодинамика и молекулярная физика.
5.1 Термодинамический метод. Макроскопические параметры. Интенсивные и экстенсивные параметры. Уравнение состояния. Первое начало термодинамики.
5.2.Обратимые и необратимые тепловые процессы. II начало термодинамики. Энтропия. Цикл Карно. Максимальный КПД тепловых машин.
5.3.Термодинамичкские потенциалы и условия равновесия. Термодинамические преобразования. Фазы и фазовые превращения.
5.4.Условия равновесия фаз. Фазовые диаграммы. Уравнение Клайперона-Клаузиуса. Критическая точка. Тройная точка.
5.5.Свойства реальных газов. Изотермы Ван-дер-Ваальса. Поверхностные явления.
5.6. Статистический и термодинамический методы. Тепловое движение. Макроскопические параметры. Уравнение состояния. Давление газа с точки зрения молекулярно-кинетической теории. Молекулярно кинетический смысл температуры.
5.7. Основная задача статистики. Фазовое пространство. Функции распределения. Распределение частиц по абсолютным значениям скорости. Средняя кинетическая энергия частицы. Скорости теплового движения частиц. Распределение Больцмана.
5.8. Понятие о физической кинетике. Экспериментальные данные о диффузии, внутреннем трении, теплопроводности в газах, жидкостях и твердых телах. Эффективное сечение рассеяния, средняя длина свободного пробега молекул в газе. Молекулярно-кинетическая теория явлений переноса в идеальном газе.
5.9. Статистическое описание квантовой системы, различие между квантово-механической и статистической вероятностью. Принцип тождественности частиц. Распределения Бозе и Ферми.
5.10. Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории. Электронный Ферми-газ в металле. Носители тока как квазичастицы. Электронная теплоемкость. Уровень Ферми. Элементы зонной теории кристаллов. Зонная структура энергетического спектра электронов. Число электронных состояний в зоне. Заполнение зон. Металлы, полупроводники, диэлектрики.
5.11. Электрический ток в вакууме. Термоэлектронная эмиссия. Электрический ток в газе. Процессы ионизации и рекомбинации. Понятие о плазме. Строение кристаллов. Точечные дефекты в кристаллах: вакансии, примеси внедрения, примеси замещения. Дислокации и пластичность.
5.12. Колебания кристаллической решетки. Понятие о фононах. Теплоемкость кристаллов при низких и высоких температурах. Модели Эйнштейна и Дебая.
5.13. Явление сверхпроводимости. Куперовское спаривание как необходимое условие сверхпроводимости. Высокотемпературные сверхпроводники.
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ
ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ № 2.
КОЛЕБАНИЯ И ВОЛНЫ
Основные формулы
• Уравнение гармонических колебаний
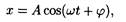
где х — смещение колеблющейся точки от положения равновесия; t — время; A, w , j — соответственно амплитуда, угловая частота, начальная фаза колебаний; ( wt + j) — фаза колебаний в момент t.
• Угловая частота колебаний
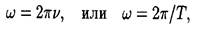
где v и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания,
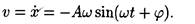
• Ускорение при гармоническом колебании
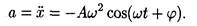
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
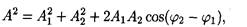
где A 1 и А2, — амплитуды составляющих колебаний; j1 и j 2 , — их начальные фазы.
• Начальная фаза j результирующего колебания может быть найдена из формулы
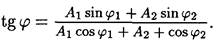
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами v 1 и v 2,
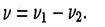
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами А1 и А2 и начальными фазами j 1 и j 2 ,
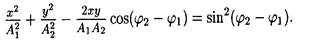
Если начальные фазы j 1 и j 2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
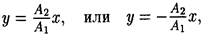
т.е. точка движется по прямой.
В том случае, если разность фаз Dj = j 2 — j 1 = p/2, уравнение принимает вид
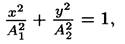
т.е. точка движется по эллипсу.
• Дифференциальное уравнение гармонических колебаний материальной точки
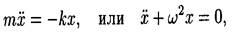
где т — масса точки; k — коэффициент квазиупругой силы
• Полная энергия материальной точки, совершающей гармонические колебания,
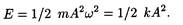
• Период колебаний тела, подвешенного на пружине (пружинный маятник),
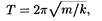
где т — масса тела; k — жесткость пружины.
Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
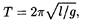
где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника
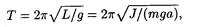
где J — момент инерции колеблющегося тела относительно оси колебаний; a - расстояние центра масс маятника от оси колебаний; L = J/(mа) - приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более » 3° ошибка в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой нити,
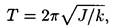
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний
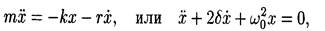
где r — коэффициент сопротивления; d — коэффициент затухания: d = r /(2 m ); ω0 — собственная угловая частота колебаний
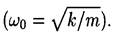
• Уравнение затухающих колебаний
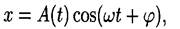
где A ( t ) — амплитуда затухающих колебаний в момент t ; ω — их угловая частота.
• Угловая частота затухающих колебаний
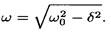
• Зависимость амплитуды затухающих колебаний от времени
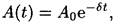
где А0 — амплитуда колебаний в момент t = 0.
• Логарифмический декремент колебаний
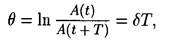
где A ( t ) и A ( t + T ) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
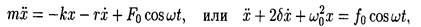
где F0 cosω t — внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 — ее амплитудное значение; f0 = F0/m.
• Амплитуда вынужденных колебаний
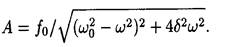
• Резонансная частота и резонансная амплитуда
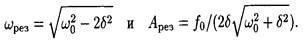
Интерференция света
• Скорость света в среде
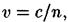
где с — скорость света в вакууме; п — абсолютный показатель преломления среды.
• Оптическая длина пути световой волны
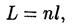
где l — геометрическая длина пути световой волны в среде с показателем преломления п.
3. Оптическая разность хода двух световых волн
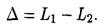
• Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе (рис. а),
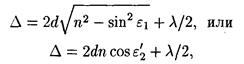
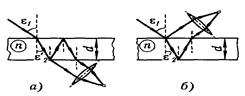
где d — толщина пластинки (пленки); e 1 — угол падения; 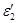 — угол преломления.
— угол преломления.
Второе слагаемое в этих формулах учитывает изменение оптической длины пути световой волны на l/2 при отражении ее от среды оптически более плотной.
В проходящем свете (рис. б) отражение световой волны происходит от среды оптически менее плотной и дополнительной разности хода световых лучей не возникает.
• Связь разности фаз Dj колебании с оптической разностью хода волн
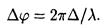
• Условие максимумов интенсивности света при интерференции
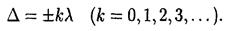
• Условие минимумов интенсивности света при интерференции
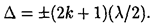
• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)
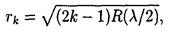
где k — номер кольца ( k = 1,2,3,...); R — радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.
Радиусы темных колец в отраженном свете (или светлых в проходящем)
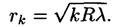
Дифракция света
• Радиус k-й зоны Френеля:
для сферической волны
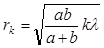
где а — расстояние диафрагмы с круглым отверстием от точечного источника света; b — расстояние диафрагмы от экрана, на котором ведется наблюдение дифракционной картины; k — номер зоны Френеля; l — длина волны;
для плоской волны
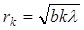
• Дифракция света на одной щели при нормальном падении лучей. Условие минимумов интенсивности света
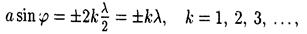
где а — ширина щели; j — угол дифракции; k — номер минимума; l — длина волны.
Условие максимумов интенсивности света
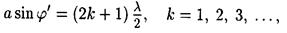
где j ' — приближенное значение угла дифракции.
• Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности

где d — период ( постоянная ) решетки; k — номер главного максимума; j — угол между нормалью к поверхности решетки и направлением дифрагированных волн.
• Разрешающая сила дифракционной решетки
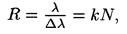
где Dl — наименьшая разность длин волн двух соседних спектральных линий (l и l+Dl), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — число штрихов решетки; k — порядковый номер дифракционного максимума.
• Угловая дисперсия дифракционной решетки
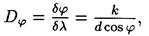
линейная дисперсия дифракционной решетки
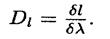
Для малых углов дифракции
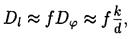
где f — главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны.
• Формула Вульфа — Брэгга
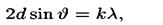
где d — расстояние между атомными плоскостями кристалла; θ — угол скольжения (угол между направлением пучка параллельных лучей, падающих на кристалл, и гранью кристалла), определяющий направление, в котором имеет место зеркальное отражение лучей (дифракционный максимум).
Законы теплового излучения.
 Закон Стефана-Больцмана
Закон Стефана-Больцмана
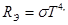
где 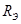 -энергетическая светимость абсолютно черного тела; Т - термодинамическая температура; s - постоянная Стефана- Больцмана [ s =5,67. 10-8 Вт/(м2.K4].
-энергетическая светимость абсолютно черного тела; Т - термодинамическая температура; s - постоянная Стефана- Больцмана [ s =5,67. 10-8 Вт/(м2.K4].
· Энергетическая светимость серого тела

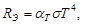
где 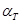 - коэффициент черноты серого тела.
- коэффициент черноты серого тела.
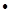 Закон смещения Вина
Закон смещения Вина
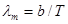 ,
,
где lm -длина волны, на которую приходится максимум энергии излучения абсолютно черного тела; b-постоянная закона смещения Вина (b = 2,90.10 -3 м . K).
 Зависимость максимальной спектральной плотности энергетической светимости от температуры
Зависимость максимальной спектральной плотности энергетической светимости от температуры
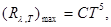

где C-постоянная [С= 1,30 . 105Вт/(м3. К5)].
Давление света.
 Давление, производимое светом при нормальном падении,
Давление, производимое светом при нормальном падении,
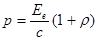 , или
, или 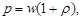

где 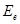 - облученность поверхности; с - скорость электромагнитного излучения в вакууме; w- объемная плотность энергии излучения в вакууме;
- облученность поверхности; с - скорость электромагнитного излучения в вакууме; w- объемная плотность энергии излучения в вакууме; 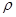 - коэффициент отражения.
- коэффициент отражения.
· Энергия фотона 

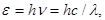
 или
или 
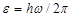 ,
,
где h - постоянная Планка; 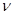 - частота света;
- частота света; 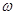 - круговая частота;
- круговая частота; 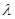 - длина волны.
- длина волны.
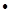 Импульс фотона выражается соответственно формулой
Импульс фотона выражается соответственно формулой
КВАНТОВАЯ ФИЗИКА.
Основные формулы.
Основные формулы.
Тепловые свойства.
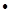 Молярная внутренняя энергия химически простых (состоящих из одинаковых атомов) твердых тел в классической теории теплоемкости выражается формулой
Молярная внутренняя энергия химически простых (состоящих из одинаковых атомов) твердых тел в классической теории теплоемкости выражается формулой

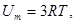
где R - молярная газовая постоянная; T - термодинамическая температура.
 Теплоемкость системы (тела) при постоянном объеме определяется как производная от внутренней энергии U по температуре, т.е.
Теплоемкость системы (тела) при постоянном объеме определяется как производная от внутренней энергии U по температуре, т.е.
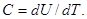
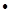 Закон Дюлонга и Пти. Молярная теплоемкость
Закон Дюлонга и Пти. Молярная теплоемкость 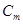 химически простых твердых тел
химически простых твердых тел
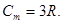
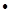 Закон Неймана - Коппа. Молярная теплоемкость химически сложных тел ( состоящих из различных атомов)
Закон Неймана - Коппа. Молярная теплоемкость химически сложных тел ( состоящих из различных атомов)
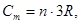
где n - общее число частиц в химической формуле соединения.
· Среднее значение энергии 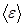 квантового осциллятора, приходящейся на одну степень свободы, в квантовой теории Эйнштейна выражается формулой
квантового осциллятора, приходящейся на одну степень свободы, в квантовой теории Эйнштейна выражается формулой
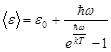 ,
,
где 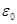 - нулевая энергия
- нулевая энергия 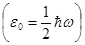 ;
; 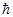 - постоянная Планка;
- постоянная Планка; 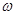 - круговая частота колебаний осциллятора; k - постоянная Больцмана;T - термодинамическая температура.
- круговая частота колебаний осциллятора; k - постоянная Больцмана;T - термодинамическая температура.
· Молярная внутренняя энергия кристалла в квантовой теории теплоемкости Эйнштейна определяется по формуле

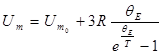 ,
,
где 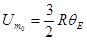 - молярная нулевая энергия по Эйнштейну;
- молярная нулевая энергия по Эйнштейну; 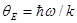 -характеристическая температура Эйнштейна.
-характеристическая температура Эйнштейна.
· Молярная теплоемкость кристалла в квантовой теории теплоемкости Эйнштейна
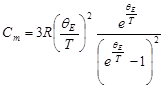 .
.
При низких температурах 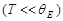
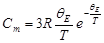 .
.
· Частотный спектр колебаний в квантовой теории теплоемкости Дебая задается функцией распределения частот g 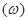 . Число
. Число 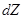 собственных частот тела, приходящихся на интервал частот от
собственных частот тела, приходящихся на интервал частот от 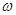 до
до 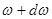 , определяется выражением
, определяется выражением
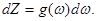
Для трехмерного кристалла, содержащего N атомов,
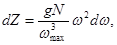
где 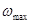 - максимальная частота, ограничивающая спектр колебаний.
- максимальная частота, ограничивающая спектр колебаний.
· Энергия U твердого тела связана со средней энергией 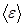 квантового осциллятора и функцией распределения частот
квантового осциллятора и функцией распределения частот 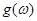 соотношением
соотношением
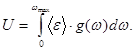
· Молярная внутренняя энергия кристалла по Дебаю
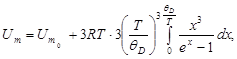
где 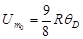 -молярная нулевая энергия кристалла по Дебаю;
-молярная нулевая энергия кристалла по Дебаю; 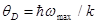 -характеристическая температура Дебая.
-характеристическая температура Дебая.
· Молярная теплоемкость кристалла по Дебаю
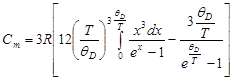 .
.
Предельный закон Дебая. В области низких температур 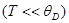 последняя формула принимает вид
последняя формула принимает вид
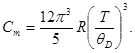
Кристаллы. Элементы кристаллографии.
· Молярный объем кристалла
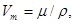
где 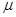 - молярная масса;
- молярная масса; 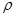 - плотность кристалла.
- плотность кристалла.
Объем 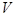 - элементарной ячейки в кристаллах:
- элементарной ячейки в кристаллах:
а) при кубической сингонии 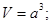
б) при гексагональной сингонии 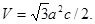 Здесь
Здесь 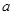 и с- параметры решетки.
и с- параметры решетки.
Если для гексагональной решетки принять теоретическое значение
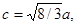 то
то 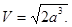
· Число 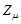 элементарных ячеек в одном моле кристалла
элементарных ячеек в одном моле кристалла
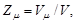 или
или 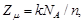
где 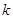 - число одинаковых атомов в химической формуле соединения (например, в кристалле
- число одинаковых атомов в химической формуле соединения (например, в кристалле 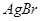 число одинаковых атомов
число одинаковых атомов 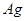 или
или 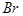 в химической формуле соединения равно единице);
в химической формуле соединения равно единице); 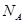 - постоянная Авогадро; n - число одинаковых атомов, приходящихся на элементарную ячейку.
- постоянная Авогадро; n - число одинаковых атомов, приходящихся на элементарную ячейку.
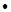 Число Z элементарных ячеек в единице объема кристалла
Число Z элементарных ячеек в единице объема кристалла
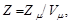
или в общем случае
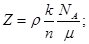
для кристалла, состоящего из одинаковых атомов (k = 1),
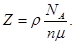
· Параметр 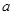 кубической решетки
кубической решетки
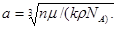
Расстояние d между соседними атомами в кубической решетке:
а) в гранецентрированной 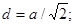
б) в объемно-центрированной 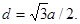
ФИЗИКА
Контрольные работы № 2.
Физика колебаний и волн.
Квантовая и атомная физика.
Термодинамика и молекулярная физика.
Технический редактор:
Подписано в печать _______________ Формат 60х90 1/16
Бумага для множительной техники
Усл.печ.л.____7.0____ Тираж _____ экз. Заказ _________

Отпечатано с авторского оригинала в центре информационных технологий СОФ МГРИ-РГГРУ
МИНОБРНАУКИ РОССИИ
СТАРООСКОЛЬСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ОБРАЗОВАНИЯ
«Российский государственный геологоразведочный университет имени
Серго Орджоникидзе»
(СОФ МГРИ-РГГРУ)
 |
А.А. Босенко
ФИЗИКА
Контрольные работы № 3,4
Физика колебаний и волн
Квантовая и атомная физика
Термодинамика и молекулярная физика
Учебное пособие
для студентов горно-геологических направлений
Старый Оскол
СОФ МГРИ - РГГРУ
2017 г
УДК 53
ББК 22.3
Рецензент: А.Х. Иванова, доцент, кандидат физико-математических наук ( Старооскольский технологический институт )
Босенко А.А.
Физика. Контрольные работы №2. Физика колебаний и волн. Квантовая и атомная физика. Термодинамика и молекулярная физика./А.А. Босенко – Старый Оскол: СОФ МГРИ - РГГРУ, 2017, – 122 с.
В пособие включены программа учебного курса и все необходимые материалы для самостоятельной работы студентов при изучении курса физики по разделам “ Физика колебаний и волн.” “Квантовая и атомная физика.” “Термодинамика и молекулярная физика.”
Для студентов технических направлений высших учебных заведений
УДК 53
ББК 22.3
© А.А. Босенко 2017 г.
ВВЕДЕНИЕ
Курс общей физики студенты заочного отделения изучают на первом и втором курсах. Занятия по расписанию (аудиторные) проводятся в форме лекций, практических, лабораторных занятий и консультаций.
Контроль знаний осуществляется при защите контрольных работ и отчетов о проделанных лабораторных работах, при сдаче зачетов и экзаменов. Содержание курса изложено в рабочей программе. Рабочая программа курса составлена на основе требований Государственного стандарта и типовой программы по физике, утвержденной Главным учебно-методическим управлением министерства образования.
Пособие содержит основной справочный материал необходимый при выполнении контрольных работ и примеры решения задач по основным темам разделов “Физика колебаний и волн. Квантовая и атомная физика. Молекулярная физика. Термодинамика.” курса физики и задачи контрольных работ.
Контрольные работы.
Контрольные работы позволяют закрепить теоретический материал. В процессе изучения третьей и четвёртой части курса физики студент должен выполнить две контрольные работы. Решение задач контрольных работ является проверкой степени усвоения студентами теоретического курса, а рецензии на работу помогают ему доработать и правильно усвоить различные разделы курса физики. Контрольные работы выполняются в период между сессиями и сдаются для проверки не позднее, чем за 15 дней до начала сессии.
Перед выполнением контрольной работы необходимо внимательно ознакомится с примерами решения задач по данной теме, уравнениями и формулами, а также со справочными материалами. Прежде, чем приступить к решению той или иной задачи, необходимо хорошо понять ее содержание и поставленные вопросы.
Решенные задачи следует оформить так, как указано ниже.
Контрольные работы, оформленные без соблюдения указанных правил, а так же работы, выполненные не по своему варианту, не будут зачтены.
При наличии значительных ошибок и неправильных решений работа возвращается студенту для исправлений. После исправления работа отправляется на кафедру физики на повторное рецензирование. Защита контрольных работ происходит в виде собеседования по решенным задачам на консультациях во время сессии.
Контрольные работы, включенные в данное пособие, распределены следующим образом: № 3 Физика колебаний и волн. № 4 Квантовая и атомная физика. Молекулярная физика. Термодинамика.
Каждая контрольная работа содержат по пять задач.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
КОНТРОЛЬНЫХ РАБОТ:
1) Контрольная работа оформляется в отдельной тетради. Титульный лист оформляется следующим образом:
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Старооскольский филиал
федерального государственного бюджетного образовательного учреждения высшего профессионального образования
"Российский государственный геологоразведочный университет имени Серго Орджоникидзе"
(СОФ МГРИ-РГГРУ)
Контрольная работа по физике N ....
“ ..........................................”
(н а з в а н и е к. р.)
студент_______ группы__________
.....................................................
( Ф. И. О. )
вариант N ...... (.................................)
н о м е р а з а д а ч
"Зачтено"
_________ дата _________ роспись преподавателя
Номер варианта соответствует двум последним цифрам номера зачётной книжки.
2) Каждая задача оформляется с начала нового листа. В начале полностью (без сокращений) записывается текст задачи так, как он приведен в методичке.
3) Все, содержащиеся в задаче данные, которые могут быть представлены в виде математических соотношений, должны быть записаны в колонке под заголовком "Дано" (краткое условие).
4) Величины, выраженные через внесистемные единицы, должны быть переведены в единицы системы СИ. Численное значение всех величин должно быть представлено в нормализованном виде: (1-9,99).10n
5) Решению задачи должно предшествовать изображение физических явлений и процессов, происходящих в данной задаче. На рисунке, чертеже или блок-схеме должны быть указаны характерные параметры данной задачи, известные и искомые физические величины.
6) Задачу рекомендуется решить сначала в общем виде, т.е. только в буквенных обозначениях, поясняя при написании формул буквенные обозначения. Решение задачи должно содержать краткие пояснения основных этапов. Значение фундаментальных физических констант, которые используются в данной задаче, должно быть приведено с указанием их численного значения и размерности в системе СИ.
7) Далее необходимо провести проверку размерности полученного выражения. Для этого в конечную формулу для искомой величины необходимо подставить вместо буквенных параметров их размерности в системе СИ. Затем преобразовать эти размерности, используя связи и соотношения между самими величинами в виде физических законов и определяющих формул. Полученная в результате проверки размерность искомой величины должна совпадать с ее размерностью в системе СИ.
8) После проверки размерности в полученную формулу для искомой величины подставить численные значения каждого из параметров задачи и записать ответ.
9) Полученное значение искомой величины должно быть проанализировано с точки зрения вероятности попадания данной величины в интервал ее возможных значений.
Данный перечень требований с необходимостью должен быть применен к каждой из задач!
10) В конце контрольной работы, после решения всех указанных в маршруте номеров задач, необходимо привести список использованной литературы.
Рабочая программа
Тема 3. Физика колебаний и волн.
3.1. Понятие о колебательных процессах. Единый подход к колебаниям различной физической природы. Кинематика гармонических колебаний. Амплитуда, частота, фаза колебаний. Сложение колебаний. Комплексная форма представления колебаний. Векторные диаграммы. Гармонический осциллятор. Маятник, груз на пружине, колебательный контур.
3.2. Свободные затухающие колебания. Коэффициент затухания, логарифмический декремент, добротность. Энергетические соотношения для осциллятора. Вынужденные колебания осциллятора под действием синусоидальной силы. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
3.3. Процесс установления колебаний. Время установления и его связь с добротностью. Параметрический резонанс. Осциллятор как спектральный прибор. Фурье-разложение. Физический смысл спектрального разложения. Модулированные колебания. Ангармонические колебания. Физические системы, содержащие нелинейность.
3.4. Волны. Плоская волна. Бегущая и стоячая волны. Фазовая скорость, длина волны, волновое число. Эффект Доплера. Продольные волны в твердом теле. Энергетические соотношения. Вектор Умова. Упругие волны в газах и жидкостях. Плоские электромагнитные волны. Вектор Пойнтинга.
3.5. Интерференция монохроматических волн. Способы получения когерентных волн и интерференционных картин. Интерферометры.
3.6. Дифракция волн. Принцип Гюйгенса-Френеля. Приближения Френеля. Простые задачи дифракции. Дифракция Фраунгофера. Дифракционная решетка.
3.7. Принцип голографии. Распространение волн в средах с дисперсией. Нормальная и аномальная дисперсия. Поглощение света. Прозрачные среды. Поляризация света. Искусственная анизотропия.
Тема 4. Квантовая физика.
4.1. Противоречия классической физики. Проблемы излучения черного тела, фотоэлектрического эффекта, стабильности и размера атома. Открытие постоянной Планка. Экспериментальное обоснование основных идей квантовой теории. Опыты Франка и Герца, Штерна и Герлаха.
4.2. Правило частот Бора. Линейчатые спектры атомов. Энергия и импульс световых квантов. Фотоэффект. Эффект Комптона. Вынужденное и спонтанное излучение фотонов.
4.3. Корпускулярно-волновой дуализм. Гипотеза де-Бройля. Микрочастица в двухщелевом интерферометре. Соотношения неопределенностей. Оценка основного состояния атома водорода и объяснение устойчивости атома.
4.4. Квантовое состояние. Задание состояния микрочастицы; волновая функция; ее статистический смысл. Суперпозиция состояний в квантовой теории. Амплитуда вероятностей. Объяснение поведения микрочастицы в интерферометре.
4.5. Уравнение Шредингера. Стационарные состояния. Частица в одномерной прямоугольной яме. Прохождение частицы под барьером. Объяснение туннельного эффекта.
4.6. Атом. Частица в сферически симметричном поле. Водородоподобные атомы. Энергетические уровни. Потенциалы возбуждения и ионизации. Принцип Паули. Периодическая система элементов Д.И. Менделеева. Молекула водорода. Физическая природа химической связи.
4.7. Атомное ядро. Строение и феноменологические модели ядра. Ядерные реакции. Радиоактивные превращения атомных ядер. Цепная реакция деления. Проблемы источников энергии. Термоядерные реакции. Энергия звезд.
Тема 5. Термодинамика и молекулярная физика.
5.1 Термодинамический метод. Макроскопические параметры. Интенсивные и экстенсивные параметры. Уравнение состояния. Первое начало термодинамики.
5.2.Обратимые и необратимые тепловые процессы. II начало термодинамики. Энтропия. Цикл Карно. Максимальный КПД тепловых машин.
5.3.Термодинамичкские потенциалы и условия равновесия. Термодинамические преобразования. Фазы и фазовые превращения.
5.4.Условия равновесия фаз. Фазовые диаграммы. Уравнение Клайперона-Клаузиуса. Критическая точка. Тройная точка.
5.5.Свойства реальных газов. Изотермы Ван-дер-Ваальса. Поверхностные явления.
5.6. Статистический и термодинамический методы. Тепловое движение. Макроскопические параметры. Уравнение состояния. Давление газа с точки зрения молекулярно-кинетической теории. Молекулярно кинетический смысл температуры.
5.7. Основная задача статистики. Фазовое пространство. Функции распределения. Распределение частиц по абсолютным значениям скорости. Средняя кинетическая энергия частицы. Скорости теплового движения частиц. Распределение Больцмана.
5.8. Понятие о физической кинетике. Экспериментальные данные о диффузии, внутреннем трении, теплопроводности в газах, жидкостях и твердых телах. Эффективное сечение рассеяния, средняя длина свободного пробега молекул в газе. Молекулярно-кинетическая теория явлений переноса в идеальном газе.
5.9. Статистическое описание квантовой системы, различие между квантово-механической и статистической вероятностью. Принцип тождественности частиц. Распределения Бозе и Ферми.
5.10. Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории. Электронный Ферми-газ в металле. Носители тока как квазичастицы. Электронная теплоемкость. Уровень Ферми. Элементы зонной теории кристаллов. Зонная структура энергетического спектра электронов. Число электронных состояний в зоне. Заполнение зон. Металлы, полупроводники, диэлектрики.
5.11. Электрический ток в вакууме. Термоэлектронная эмиссия. Электрический ток в газе. Процессы ионизации и рекомбинации. Понятие о плазме. Строение кристаллов. Точечные дефекты в кристаллах: вакансии, примеси внедрения, примеси замещения. Дислокации и пластичность.
5.12. Колебания кристаллической решетки. Понятие о фононах. Теплоемкость кристаллов при низких и высоких температурах. Модели Эйнштейна и Дебая.
5.13. Явление сверхпроводимости. Куперовское спаривание как необходимое условие сверхпроводимости. Высокотемпературные сверхпроводники.
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ
ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ № 2.
КОЛЕБАНИЯ И ВОЛНЫ
Основные формулы
• Уравнение гармонических колебаний
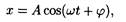
где х — смещение колеблющейся точки от положения равновесия; t — время; A, w , j — соответственно амплитуда, угловая частота, начальная фаза колебаний; ( wt + j) — фаза колебаний в момент t.
• Угловая частота колебаний
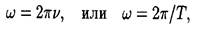
где v и Т — частота и период колебаний.
• Скорость точки, совершающей гармонические колебания,
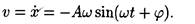
• Ускорение при гармоническом колебании
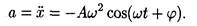
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
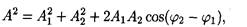
где A 1 и А2, — амплитуды составляющих колебаний; j1 и j 2 , — их начальные фазы.
• Начальная фаза j результирующего колебания может быть найдена из формулы
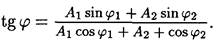
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами v 1 и v 2,
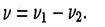
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами А1 и А2 и начальными фазами j 1 и j 2 ,
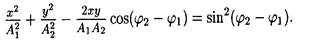
Если начальные фазы j 1 и j 2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
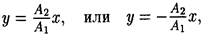
т.е. точка движется по прямой.
В том случае, если разность фаз Dj = j 2 — j 1 = p/2, уравнение принимает вид
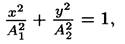
т.е. точка движется по эллипсу.
• Дифференциальное уравнение гармонических колебаний материальной точки
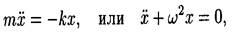
где т — масса точки; k — коэффициент квазиупругой силы
• Полная энергия материальной точки, совершающей гармонические колебания,
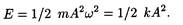
• Период колебаний тела, подвешенного на пружине (пружинный маятник),
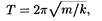
где т — масса тела; k — жесткость пружины.
Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела).
Период колебаний математического маятника
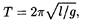
где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника
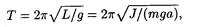
где J — момент инерции колеблющегося тела относительно оси колебаний; a - расстояние центра масс маятника от оси колебаний; L = J/(mа) - приведенная длина физического маятника.
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более » 3° ошибка в значении периода не превышает 1 %.
Период крутильных колебаний тела, подвешенного на упругой нити,
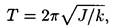
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.
• Дифференциальное уравнение затухающих колебаний
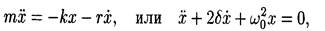
где r — коэффициент сопротивления; d — коэффициент затухания: d = r /(2 m ); ω0 — собственная угловая частота колебаний
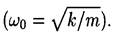
• Уравнение затухающих колебаний
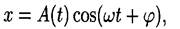
где A ( t ) — амплитуда затухающих колебаний в момент t ; ω — их угловая частота.
• Угловая частота затухающих колебаний
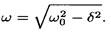
• Зависимость амплитуды затухающих колебаний от времени
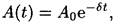
где А0 — амплитуда колебаний в момент t = 0.
• Логарифмический декремент колебаний
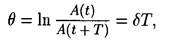
где A ( t ) и A ( t + T ) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период.
• Дифференциальное уравнение вынужденных колебаний
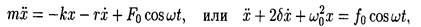
где F0 cosω t — внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания; F0 — ее амплитудное значение; f0 = F0/m.
• Амплитуда вынужденных колебаний
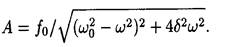
• Резонансная частота и резонансная амплитуда
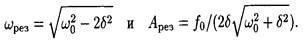
Дата: 2019-02-19, просмотров: 342.