 Распределение Больцмана (распределение частиц в силовом поле)
Распределение Больцмана (распределение частиц в силовом поле)
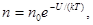
где n - концентрация частиц; U - их потенциальная энергия; no - концентрация частиц в точках поля, где U = 0; k - постоянная Больцмана; T - термодинамическая температура; e - основание натуральных логарифмов.
 Барометрическая формула (распределение давления в однородном поле силы тяжести)
Барометрическая формула (распределение давления в однородном поле силы тяжести)
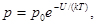 или
или 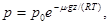
где p - давление газа; m - масса частицы; 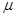 - молярная масса; z - координата (высота) точки по отношению к уровню, принятому за нулевой; po - давление на этом уровне;
- молярная масса; z - координата (высота) точки по отношению к уровню, принятому за нулевой; po - давление на этом уровне; 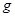 - ускорение свободного падения; R - молярная газовая постоянная.
- ускорение свободного падения; R - молярная газовая постоянная.
· Вероятность того, что физическая величина x, характеризующая молекулу. лежит интервале значений от 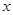 до
до 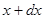 ,
,
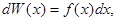
где f(x) - функция распределения молекул по значениям данной физической величины x (плотность вероятности).
· Количество молекул, для которых физическая величина x, характеризующая их, заключена в интервале значений от 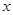 до
до 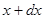 ,
,
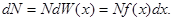 .
.
· Распределение Максвелла (распределение молекул по скоростям) выражается двумя соотношениями:
а) число молекул, скорости которых заключены в пределах от 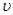 до
до 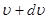 ,
,
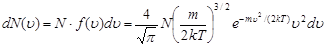 ,
,
где 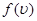 - функция распределения молекул по модулям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от
- функция распределения молекул по модулям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от 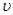 до
до 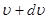 , к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале; N - общее число молекул; m - масса молекулы;
, к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале; N - общее число молекул; m - масса молекулы;
б) число молекул, относительные скорости которых заключены в пределах от u до u+du,
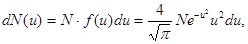
где u= 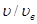 - относительная скорость, равная отношению скорости
- относительная скорость, равная отношению скорости 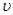 к наивероятнейшей скорости
к наивероятнейшей скорости 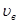 ; f(u) - функция распределения по относительным скоростям.
; f(u) - функция распределения по относительным скоростям.
 Распределение молекул по импульсам. Число молекул, импульсы которых заключены в пределах от
Распределение молекул по импульсам. Число молекул, импульсы которых заключены в пределах от 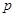 до
до 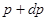 ,
,
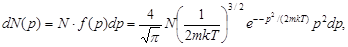
где 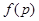 - функция распределения по импульсам.
- функция распределения по импульсам.
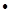 Распределение молекул по кинетическим энергиям поступательного движения. Число молекул, энергии которых заключены в интервале от
Распределение молекул по кинетическим энергиям поступательного движения. Число молекул, энергии которых заключены в интервале от 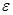 до
до 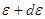 ,
,
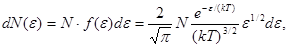
где 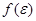 - функция распределения по кинетическим энергиям.
- функция распределения по кинетическим энергиям.
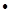 Среднее значение физической величины x в общем случае
Среднее значение физической величины x в общем случае
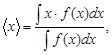
а в том случае если функция распределения нормирована на единицу,
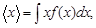
где 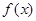 - функция распределения, а интегрирование ведется по всей совокупности изменений величины x.
- функция распределения, а интегрирование ведется по всей совокупности изменений величины x.
Например, среднее значение скорости молекулы (т.е. средняя арифметическая скорость) 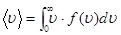 ; средняя квадратичная скорость
; средняя квадратичная скорость 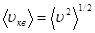 , где
, где 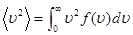 ; средняя кинетическая энергия поступательного движения молекулы
; средняя кинетическая энергия поступательного движения молекулы
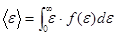 .
.
Тепловые свойства.
 Молярная внутренняя энергия химически простых (состоящих из одинаковых атомов) твердых тел в классической теории теплоемкости выражается формулой
Молярная внутренняя энергия химически простых (состоящих из одинаковых атомов) твердых тел в классической теории теплоемкости выражается формулой

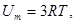
где R - молярная газовая постоянная; T - термодинамическая температура.
 Теплоемкость системы (тела) при постоянном объеме определяется как производная от внутренней энергии U по температуре, т.е.
Теплоемкость системы (тела) при постоянном объеме определяется как производная от внутренней энергии U по температуре, т.е.
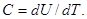
 Закон Дюлонга и Пти. Молярная теплоемкость
Закон Дюлонга и Пти. Молярная теплоемкость 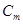 химически простых твердых тел
химически простых твердых тел
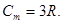
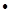 Закон Неймана - Коппа. Молярная теплоемкость химически сложных тел ( состоящих из различных атомов)
Закон Неймана - Коппа. Молярная теплоемкость химически сложных тел ( состоящих из различных атомов)
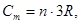
где n - общее число частиц в химической формуле соединения.
· Среднее значение энергии 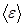 квантового осциллятора, приходящейся на одну степень свободы, в квантовой теории Эйнштейна выражается формулой
квантового осциллятора, приходящейся на одну степень свободы, в квантовой теории Эйнштейна выражается формулой
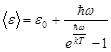 ,
,
где 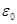 - нулевая энергия
- нулевая энергия 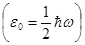 ;
; 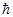 - постоянная Планка;
- постоянная Планка; 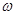 - круговая частота колебаний осциллятора; k - постоянная Больцмана;T - термодинамическая температура.
- круговая частота колебаний осциллятора; k - постоянная Больцмана;T - термодинамическая температура.
· Молярная внутренняя энергия кристалла в квантовой теории теплоемкости Эйнштейна определяется по формуле

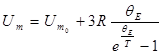 ,
,
где 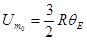 - молярная нулевая энергия по Эйнштейну;
- молярная нулевая энергия по Эйнштейну; 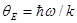 -характеристическая температура Эйнштейна.
-характеристическая температура Эйнштейна.
· Молярная теплоемкость кристалла в квантовой теории теплоемкости Эйнштейна
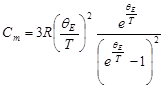 .
.
При низких температурах 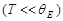
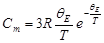 .
.
· Частотный спектр колебаний в квантовой теории теплоемкости Дебая задается функцией распределения частот g  . Число
. Число  собственных частот тела, приходящихся на интервал частот от
собственных частот тела, приходящихся на интервал частот от 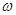 до
до 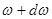 , определяется выражением
, определяется выражением
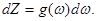
Для трехмерного кристалла, содержащего N атомов,
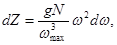
где 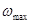 - максимальная частота, ограничивающая спектр колебаний.
- максимальная частота, ограничивающая спектр колебаний.
· Энергия U твердого тела связана со средней энергией 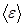 квантового осциллятора и функцией распределения частот
квантового осциллятора и функцией распределения частот 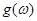 соотношением
соотношением
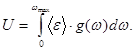
· Молярная внутренняя энергия кристалла по Дебаю
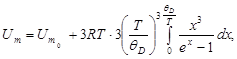
где 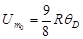 -молярная нулевая энергия кристалла по Дебаю;
-молярная нулевая энергия кристалла по Дебаю; 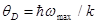 -характеристическая температура Дебая.
-характеристическая температура Дебая.
· Молярная теплоемкость кристалла по Дебаю
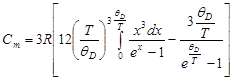 .
.
Предельный закон Дебая. В области низких температур 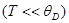 последняя формула принимает вид
последняя формула принимает вид
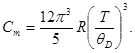
Кристаллы. Элементы кристаллографии.
· Молярный объем кристалла
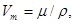
где 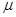 - молярная масса;
- молярная масса; 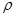 - плотность кристалла.
- плотность кристалла.
Объем 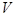 - элементарной ячейки в кристаллах:
- элементарной ячейки в кристаллах:
а) при кубической сингонии 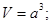
б) при гексагональной сингонии 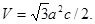 Здесь
Здесь 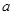 и с- параметры решетки.
и с- параметры решетки.
Если для гексагональной решетки принять теоретическое значение
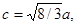 то
то 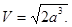
· Число 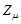 элементарных ячеек в одном моле кристалла
элементарных ячеек в одном моле кристалла
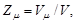 или
или 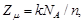
где 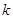 - число одинаковых атомов в химической формуле соединения (например, в кристалле
- число одинаковых атомов в химической формуле соединения (например, в кристалле 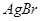 число одинаковых атомов
число одинаковых атомов 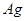 или
или 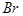 в химической формуле соединения равно единице);
в химической формуле соединения равно единице); 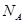 - постоянная Авогадро; n - число одинаковых атомов, приходящихся на элементарную ячейку.
- постоянная Авогадро; n - число одинаковых атомов, приходящихся на элементарную ячейку.
 Число Z элементарных ячеек в единице объема кристалла
Число Z элементарных ячеек в единице объема кристалла
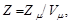
или в общем случае
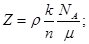
для кристалла, состоящего из одинаковых атомов (k = 1),
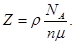
· Параметр 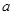 кубической решетки
кубической решетки
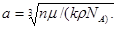
Расстояние d между соседними атомами в кубической решетке:
а) в гранецентрированной 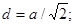
б) в объемно-центрированной 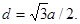
Дата: 2019-02-19, просмотров: 328.