Понятие неопределенного интеграла. Свойства неопределенного интеграла. Таблица основных неопределенных интегралов [3, §29]. Основные методы интегрирования [3, §30]. Интегрирование рациональных функций [3, §31]. Интегрирование тригоно-метрических функций [3, §32]. Интегрирование иррациональных функций [3, §33].
Пример 9.  Найти неопределенные интегралы:
Найти неопределенные интегралы:
а) 
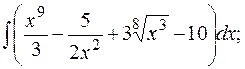 б)
б) 
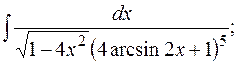
в) 
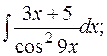 г)
г) 
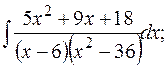 д)
д) 
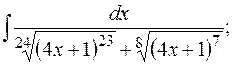
е) 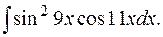
Решение.
а) 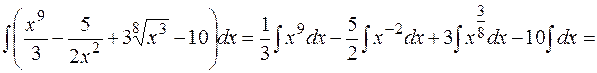
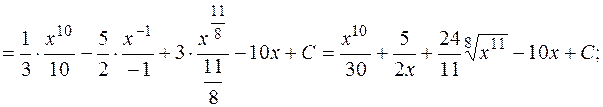
б) 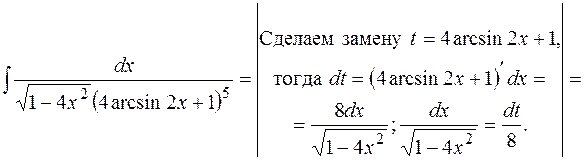
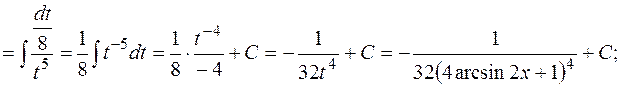
в) 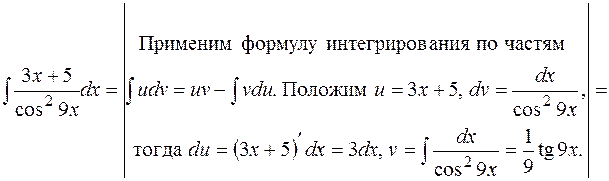
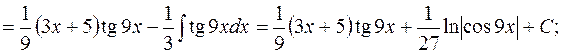
г) подынтегральная дробь – правильная, но ее знаменатель не до конца разложен на множители. Поэтому преобразуем знаменатель
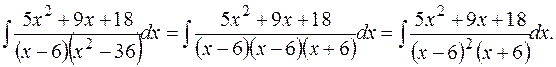
Разложим подынтегральную дробь на сумму простейших дробей
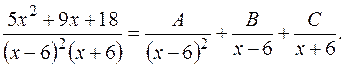
Неизвестные коэффициенты 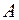 ,
, 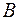 ,
,  найдем методом частных значений. Так как
найдем методом частных значений. Так как
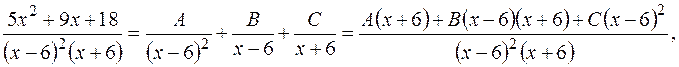 то
то 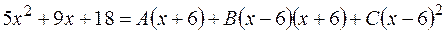 .
.
Положим 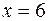 , тогда
, тогда 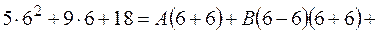
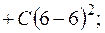
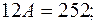
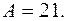
Положим 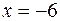 , тогда
, тогда 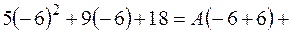
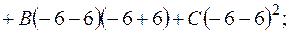
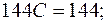
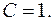
Так как «удобных» частных значений не осталось, то придадим 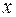 любое значение, например
любое значение, например 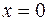 . Получим
. Получим 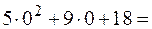
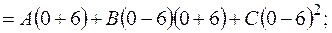
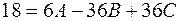 или
или 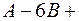
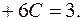 Откуда с учетом найденных значений
Откуда с учетом найденных значений 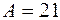 и
и 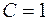 , имеем
, имеем 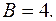
Значит, 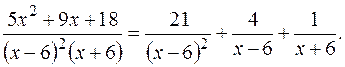 Тогда
Тогда
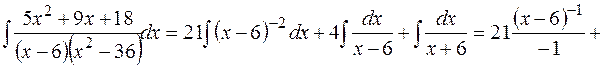
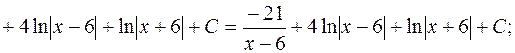
д) наименьшее общее кратное показателей корней в подынтегральном выражении равно 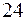 , поэтому сделаем подстановку
, поэтому сделаем подстановку 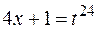 , получим
, получим
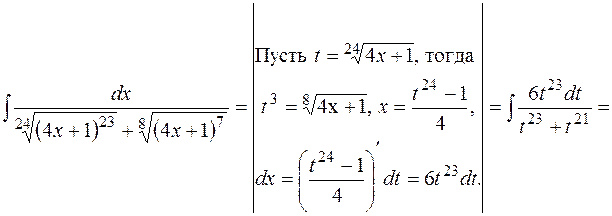
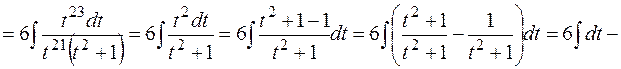
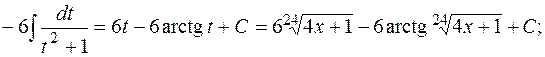
е) 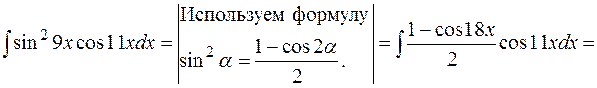
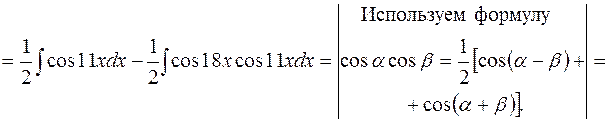
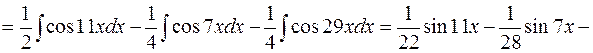
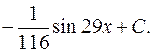
Тема 5. определенный интеграл
Определенный интеграл [3, §35]. Свойства определенного интеграла [3, §38]. Формула Ньютона-Лейбница [3, §37]. Вычисление определенного интеграла [3, §39]. Несобственные интегралы [3, §40]. Геометрические и физические приложения определенного интеграла [3, §41].
Пример 10. Найти площадь фигуры, ограниченной линиями 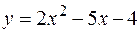 ,
, 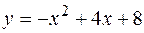 .
.
Решение. Площадь фигуры, ограниченной кривыми 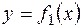 и
и
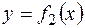 , причем
, причем 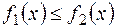 , прямыми
, прямыми 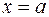 и
и 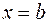 , вычисляется по формуле
, вычисляется по формуле 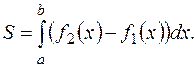
Найдем абсциссы точек пересечения заданных парабол. Для этого решим систему уравнений 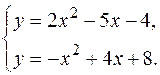
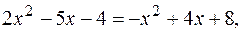 откуда
откуда 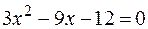 или
или 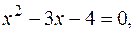
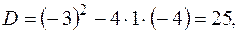
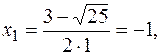
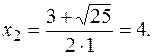
Сделаем чертеж.
 |
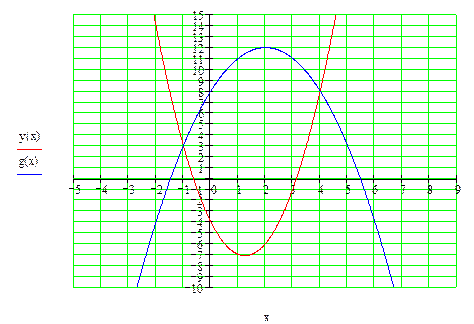
Таким образом,
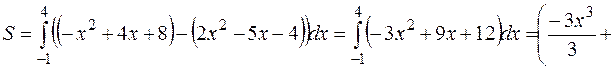
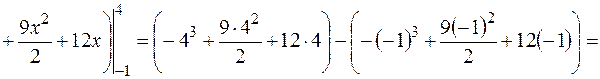
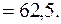
Пример 11. Найти объем тела, образованного вращением вокруг оси 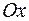 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 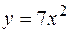 , прямой
, прямой 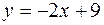 и осью
и осью 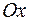 .
.
Решение. Объем тела вращения, образованного вращением вокруг оси 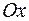 криволинейной трапеции, ограниченной кривой
криволинейной трапеции, ограниченной кривой 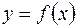 и прямыми
и прямыми 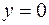 ,
, 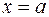 ,
, 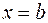 , вычисляется по формуле
, вычисляется по формуле 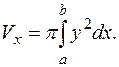
 Найдем абсциссу точки пересечения заданной параболы и заданной прямой в первой четверти. Для этого решим систему уравнений
Найдем абсциссу точки пересечения заданной параболы и заданной прямой в первой четверти. Для этого решим систему уравнений 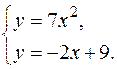
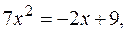 откуда
откуда 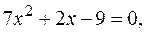
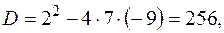
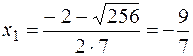 ,
, 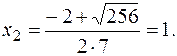 Первой четверти соответствует корень
Первой четверти соответствует корень 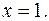
Найдем абсциссу точки пересечения заданной прямой с осью 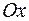 :
: 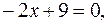
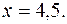
Сделаем чертеж.
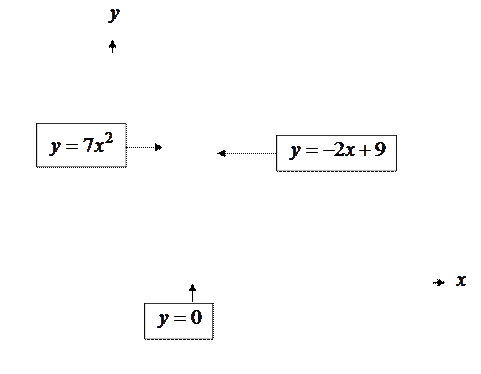 |
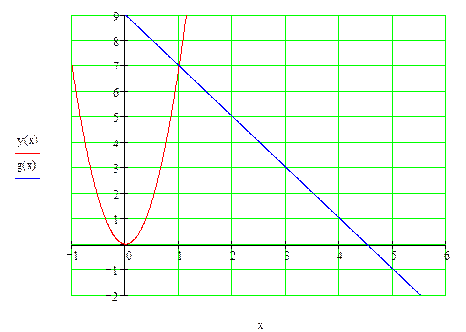
Таким образом, тело вращения при 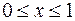 ограничено поверхностью, образованной вращением параболы
ограничено поверхностью, образованной вращением параболы 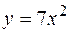 вокруг оси
вокруг оси 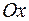 , а при
, а при 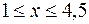 – вращением прямой
– вращением прямой 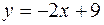 вокруг оси
вокруг оси 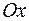 .
.
Следовательно, искомый объем 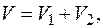 где
где
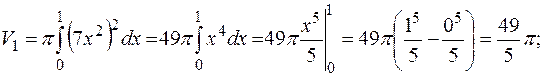
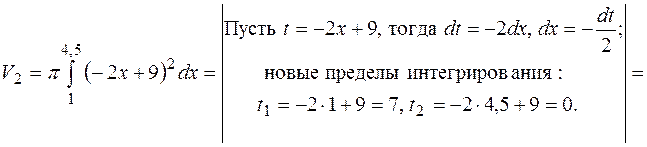
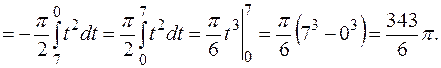
Значит, 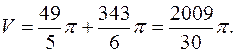
Тема 6. двойной интеграл
Двойной интеграл [4, §7.1]. Основные свойства двойного интеграла [4, §7.3]. Вычисление двойного интеграла в декартовых координатах [4, §7.4]. Вычисление двойного интеграла в полярных координатах [4, §7.5]. Приложения двойного интеграла [4, §7.6].
Пример 11. Записать двойной интеграл 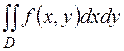 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 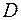 ограничена линиями
ограничена линиями 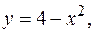
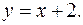
Решение. Найдем точки пересечения заданных линий. Для этого решим систему уравнений 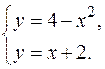
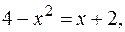 откуда
откуда 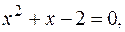
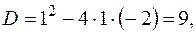
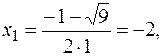
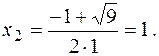
Соответственно 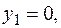
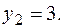
Изобразим область  .
. 
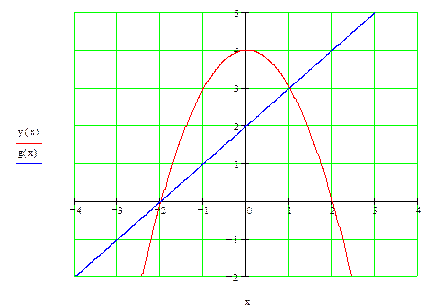
С одной стороны, область 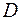 можно описать как часть плоскости, расположенную в полосе между прямыми
можно описать как часть плоскости, расположенную в полосе между прямыми 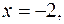
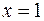 и линиями
и линиями 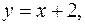
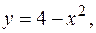 и тогда
и тогда
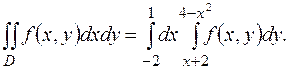
С другой стороны, область 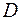 можно представить в виде
можно представить в виде 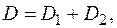 где область
где область 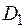 – часть плоскости, расположенная в горизонтальной полосе между прямыми
– часть плоскости, расположенная в горизонтальной полосе между прямыми 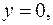
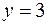 и линиями
и линиями 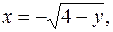
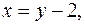 область
область 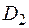 – часть плоскости, расположенная в горизонтальной полосе между прямыми
– часть плоскости, расположенная в горизонтальной полосе между прямыми 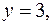
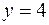 и линиями
и линиями 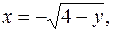
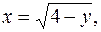 и тогда
и тогда
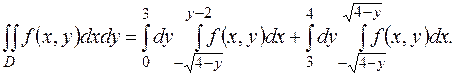
Пример 12. Найти массу пластинки, ограниченной линиями 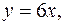
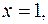
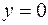 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 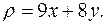
Решение. Если пластинка занимает область 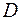 плоскости
плоскости 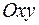 и имеет переменную поверхностную плотность
и имеет переменную поверхностную плотность 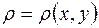 , то масса пластинки выражается двойным интегралом
, то масса пластинки выражается двойным интегралом 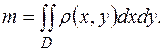
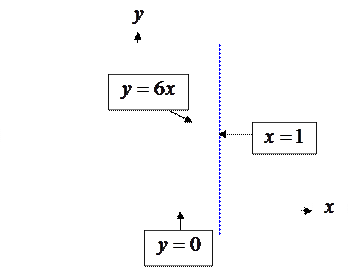 Сделаем чертеж.
Сделаем чертеж.

|
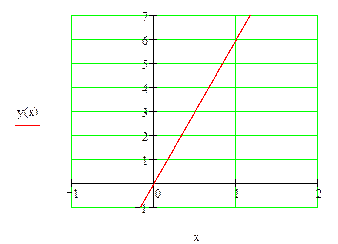
Имеем 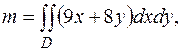 где область интегрирования
где область интегрирования 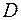 – часть плоскости, расположенная в полосе между прямыми
– часть плоскости, расположенная в полосе между прямыми 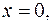
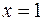 и линиями
и линиями 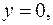
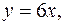 тогда
тогда
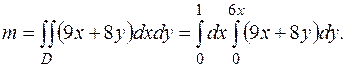
Вычислим внутренний интеграл по переменной 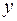 , считая
, считая 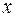 константой:
константой:
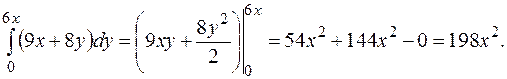
Вычислим внешний интеграл от функции 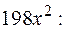
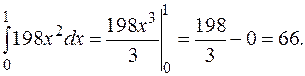
Таким образом, масса пластинки равна 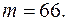
Дата: 2019-02-25, просмотров: 343.