УТВЕРЖДАЮ
Ректор университета
__________ О.Н. Федонин
«___»____________2013г.
МАТЕМАТИКА
Методические указания к изучению дисциплины
для студентов заочной формы обучения направлений подготовки
151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение»
(II семестр)
Брянск 2013
УДК 511
Математика [Текст]+[Электронный ресурс]: методические указания к изучению дисциплины для студентов заочной формы обучения направлений подготовки 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение» (II семестр). – Брянск: БГТУ, 2013. – 43 с.
Разработали: Е.С. Золотухина, канд. физ.-мат. наук, доц.;
А.И. Горелёнков, канд. техн. наук, доц.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол №3 от 19.11.12)
ПРЕДИСЛОВИЕ
Настоящие МУ предназначены для оказания помощи студентам при изучении дисциплины «Математика» во втором семестре. Они содержат список рекомендуемой литературы, методические рекомендации к изучению тем курса и выполнению контрольных работ и задачи для контрольных работ.
По дисциплине «Математика» студенты во втором семестре сдают экзамен после выполнения предусмотренных учебным планом двух контрольных работ. Задания к ним приводятся в данных указаниях. При выполнении работ и их оформлении следует придерживаться следующих правил:
– студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки;
– работа должна быть выполнена в тетради, имеющей поля для замечаний рецензента;
– перед решением каждой задачи нужно привести полностью ее условие;
– следует придерживаться той последовательности при решении задач, в какой они даны в задании;
– на обложке тетради указываются наименование учебной дисциплины, номер контрольной работы, фамилия, имя, отчество (полностью) студента, номер его группы и зачетной книжки, фамилия, имя, отчество рецензента.
Список рекомендуемой литературы
1. Пискунов, Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Интеграл-Пресс, 2004. – Т. 1. – 416 с.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Интеграл-Пресс, 2001. – Т. 2. – 544 с.
3. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1. − 288 с.
4. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 2. − 254 с.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ ТЕМ КУРСА И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Тема 6. двойной интеграл
Двойной интеграл [4, §7.1]. Основные свойства двойного интеграла [4, §7.3]. Вычисление двойного интеграла в декартовых координатах [4, §7.4]. Вычисление двойного интеграла в полярных координатах [4, §7.5]. Приложения двойного интеграла [4, §7.6].
Пример 11. Записать двойной интеграл 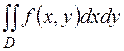 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 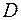 ограничена линиями
ограничена линиями 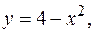
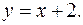
Решение. Найдем точки пересечения заданных линий. Для этого решим систему уравнений 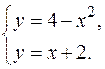
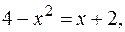 откуда
откуда 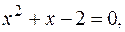
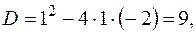
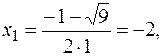
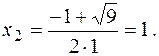
Соответственно 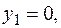
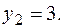
Изобразим область 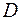 .
. 
С одной стороны, область 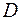 можно описать как часть плоскости, расположенную в полосе между прямыми
можно описать как часть плоскости, расположенную в полосе между прямыми 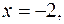
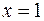 и линиями
и линиями 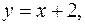
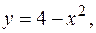 и тогда
и тогда
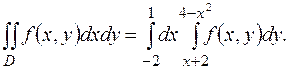
С другой стороны, область 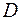 можно представить в виде
можно представить в виде 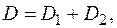 где область
где область 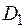 – часть плоскости, расположенная в горизонтальной полосе между прямыми
– часть плоскости, расположенная в горизонтальной полосе между прямыми 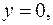
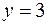 и линиями
и линиями 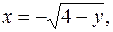
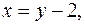 область
область 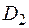 – часть плоскости, расположенная в горизонтальной полосе между прямыми
– часть плоскости, расположенная в горизонтальной полосе между прямыми 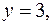
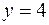 и линиями
и линиями 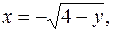
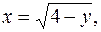 и тогда
и тогда
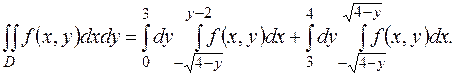
Пример 12. Найти массу пластинки, ограниченной линиями 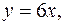
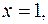
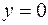 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 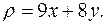
Решение. Если пластинка занимает область 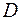 плоскости
плоскости 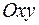 и имеет переменную поверхностную плотность
и имеет переменную поверхностную плотность 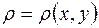 , то масса пластинки выражается двойным интегралом
, то масса пластинки выражается двойным интегралом 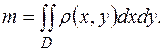
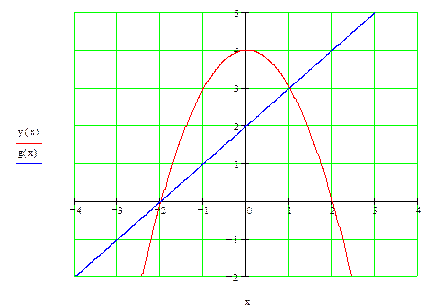
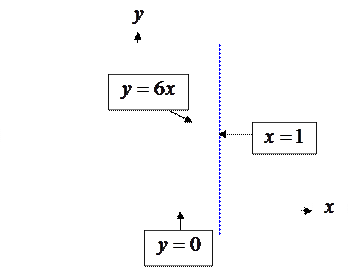 Сделаем чертеж.
Сделаем чертеж.

|
Имеем 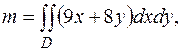 где область интегрирования
где область интегрирования 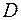 – часть плоскости, расположенная в полосе между прямыми
– часть плоскости, расположенная в полосе между прямыми 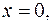
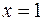 и линиями
и линиями 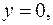
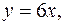 тогда
тогда
Вычислим внутренний интеграл по переменной 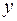 , считая
, считая 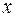 константой:
константой:
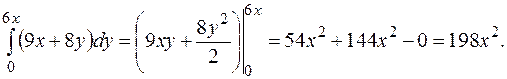
Вычислим внешний интеграл от функции 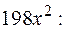
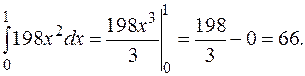
Таким образом, масса пластинки равна 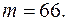
ВАРИАНТ 1
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 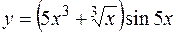 ;
;
б) 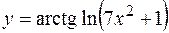 ;
;
в) 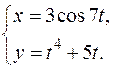
2. Найти производную второго порядка для функции 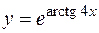 .
.
3. Исследовать функцию 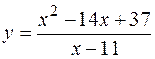 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 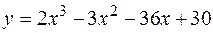 на отрезке
на отрезке 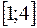 .
.
5. Найти частные производные первого порядка функции 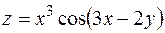 .
.
6. Найти дифференциал второго порядка функции 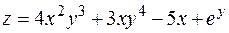 .
.
7. Найти градиент и производную функции 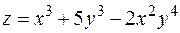 в точке
в точке 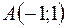 по направлению вектора
по направлению вектора 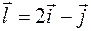 .
.
8. Найти экстремумы функции 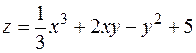 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 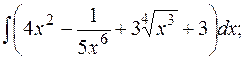
б) 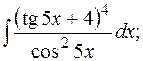
в) 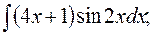
г) 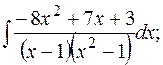
д) 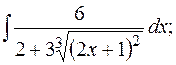
е) 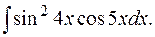
2. Найти площадь фигуры, ограниченной линиями 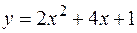 ,
, 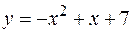 .
.
3. Найти объем тела, образованного вращением вокруг оси 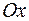 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 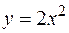 , прямой
, прямой 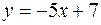 и осью
и осью 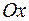 .
.
4. Записать двойной интеграл 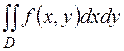 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 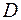 ограничена линиями
ограничена линиями 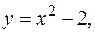
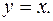
5. Найти массу пластинки, ограниченной линиями 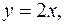
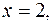
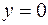 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 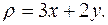
ВАРИАНТ 2
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 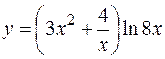 ;
;
б) 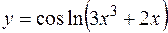 ;
;
в) 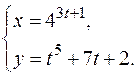
2. Найти производную второго порядка для функции 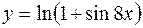 .
.
3. Исследовать функцию 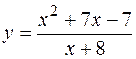 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 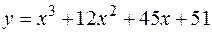 на отрезке
на отрезке 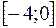 .
.
5. Найти частные производные первого порядка функции 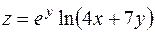 .
.
6. Найти дифференциал второго порядка функции 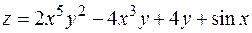 .
.
7. Найти градиент и производную функции 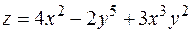 в точке
в точке 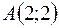 по направлению вектора
по направлению вектора 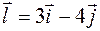 .
.
8. Найти экстремумы функции 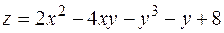 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 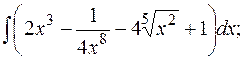
б) 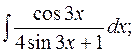
в) 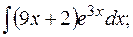
г) 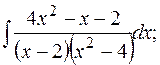
д) 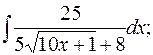
е) 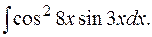
2. Найти площадь фигуры, ограниченной линиями 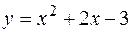 ,
, 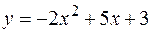 .
.
3. Найти объем тела, образованного вращением вокруг оси 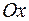 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 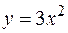 , прямой
, прямой 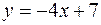 и осью
и осью 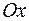 .
.
4. Записать двойной интеграл 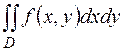 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 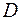 ограничена линиями
ограничена линиями 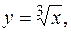
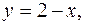 осью
осью 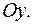
5. Найти массу пластинки, ограниченной линиями 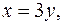
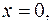
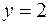 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 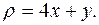
ВАРИАНТ 3
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 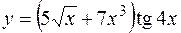 ;
;
б) 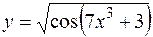 ;
;
в) 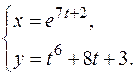
2. Найти производную второго порядка для функции 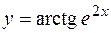 .
.
3. Исследовать функцию 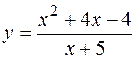 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 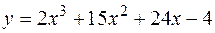 на отрезке
на отрезке 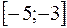 .
.
5. Найти частные производные первого порядка функции 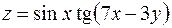 .
.
6. Найти дифференциал второго порядка функции 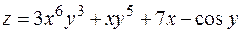 .
.
7. Найти градиент и производную функции 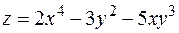 в точке
в точке 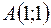 по направлению вектора
по направлению вектора 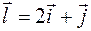 .
.
8. Найти экстремумы функции 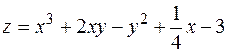 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 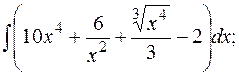
б) 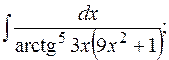
в) 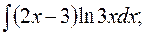
г) 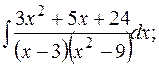
д) 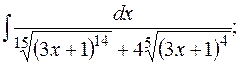
е) 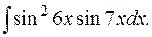
2. Найти площадь фигуры, ограниченной линиями 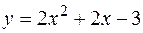 ,
, 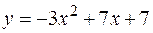 .
.
3. Найти объем тела, образованного вращением вокруг оси 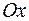 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 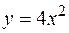 , прямой
, прямой 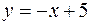 и осью
и осью 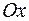 .
.
4. Записать двойной интеграл 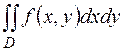 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 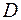 ограничена линиями
ограничена линиями 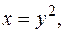
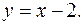
5. Найти массу пластинки, ограниченной линиями 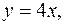
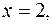
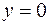 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 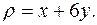
ВАРИАНТ 4
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 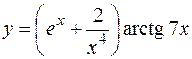 ;
;
б) 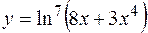 ;
;
в) 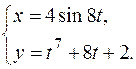
2. Найти производную второго порядка для функции 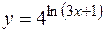 .
.
3. Исследовать функцию 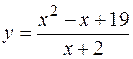 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 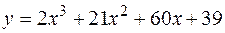 на отрезке
на отрезке 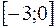 .
.
5. Найти частные производные первого порядка функции 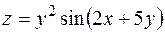 .
.
6. Найти дифференциал второго порядка функции 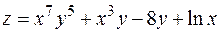 .
.
7. Найти градиент и производную функции 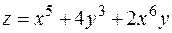 в точке
в точке 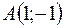 по направлению вектора
по направлению вектора 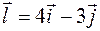 .
.
8. Найти экстремумы функции 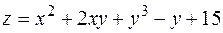 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 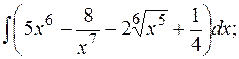
б) 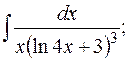
в) 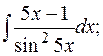
г) 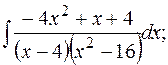
д) 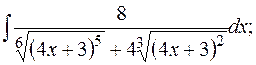
е) 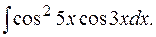
2. Найти площадь фигуры, ограниченной линиями 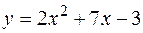 ,
, 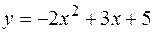 .
.
3. Найти объем тела, образованного вращением вокруг оси 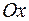 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 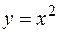 , прямой
, прямой 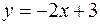 и осью
и осью 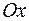 .
.
4. Записать двойной интеграл 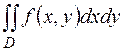 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 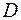 ограничена линиями
ограничена линиями 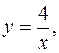
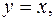
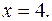
5. Найти массу пластинки, ограниченной линиями 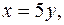
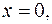
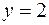 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 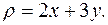
ВАРИАНТ 5
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 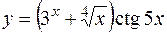 ;
;
б) 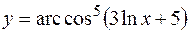 ;
;
в) 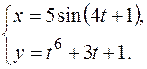
2. Найти производную второго порядка для функции 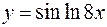 .
.
3. Исследовать функцию 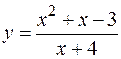 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 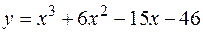 на отрезке
на отрезке 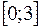 .
.
5. Найти частные производные первого порядка функции 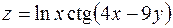 .
.
6. Найти дифференциал второго порядка функции 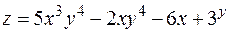 .
.
7. Найти градиент и производную функции 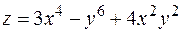 в точке
в точке 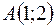 по направлению вектора
по направлению вектора 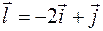 .
.
8. Найти экстремумы функции 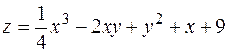 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 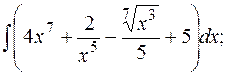
б) 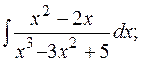
в) 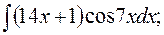
г) 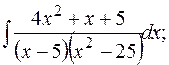
д) 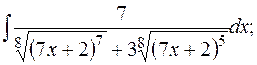
е) 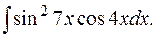
2. Найти площадь фигуры, ограниченной линиями 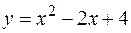 ,
, 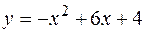 .
.
3. Найти объем тела, образованного вращением вокруг оси 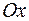 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 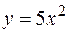 , прямой
, прямой 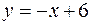 и осью
и осью 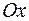 .
.
4. Записать двойной интеграл 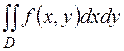 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 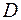 ограничена линиями
ограничена линиями 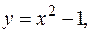
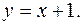
5. Найти массу пластинки, ограниченной линиями 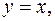
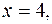
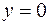 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 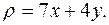
ВАРИАНТ 6
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 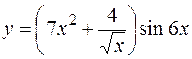 ;
;
б) 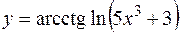 ;
;
в) 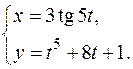
2. Найти производную второго порядка для функции 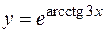 .
.
3. Исследовать функцию 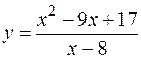 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 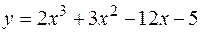 на отрезке
на отрезке 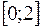 .
.
5. Найти частные производные первого порядка функции 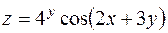 .
.
6. Найти дифференциал второго порядка функции 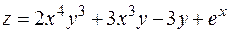 .
.
7. Найти градиент и производную функции 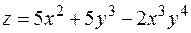 в точке
в точке 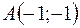 по направлению вектора
по направлению вектора 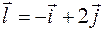 .
.
8. Найти экстремумы функции 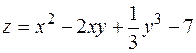 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 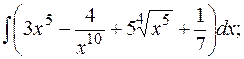
б) 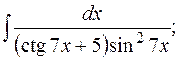
в) 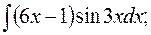
г) 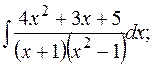
д) 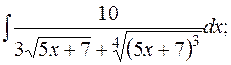
е) 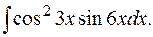
2. Найти площадь фигуры, ограниченной линиями 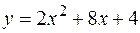 ,
, 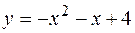 .
.
3. Найти объем тела, образованного вращением вокруг оси 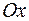 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 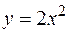 , прямой
, прямой 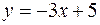 и осью
и осью 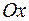 .
.
4. Записать двойной интеграл 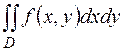 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 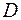 ограничена линиями
ограничена линиями 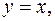
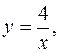
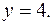
5. Найти массу пластинки, ограниченной линиями 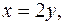
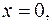
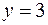 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 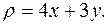
ВАРИАНТ 7
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 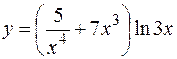 ;
;
б) 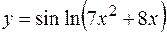 ;
;
в) 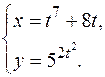
2. Найти производную второго порядка для функции 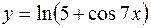 .
.
3. Исследовать функцию 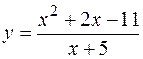 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 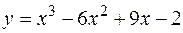 на отрезке
на отрезке 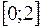 .
.
5. Найти частные производные первого порядка функции 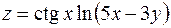 .
.
6. Найти дифференциал второго порядка функции 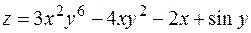 .
.
7. Найти градиент и производную функции 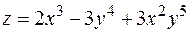 в точке
в точке 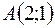 по направлению вектора
по направлению вектора 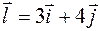 .
.
8. Найти экстремумы функции 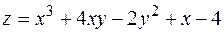 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 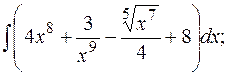
б) 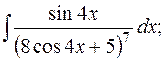
в) 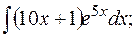
г) 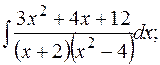
д) 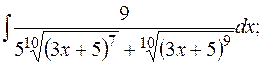
е) 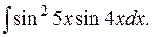
2. Найти площадь фигуры, ограниченной линиями 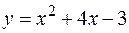 ,
, 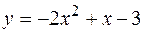 .
.
3. Найти объем тела, образованного вращением вокруг оси 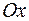 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 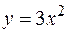 , прямой
, прямой 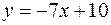 и осью
и осью 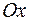 .
.
4. Записать двойной интеграл 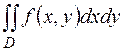 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 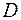 ограничена линиями
ограничена линиями 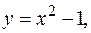
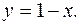
5. Найти массу пластинки, ограниченной линиями 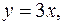
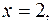
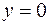 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 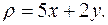
ВАРИАНТ 8
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 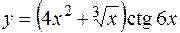 ;
;
б) 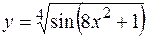 ;
;
в) 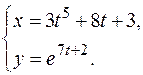
2. Найти производную второго порядка для функции 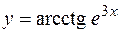 .
.
3. Исследовать функцию 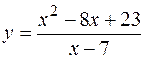 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 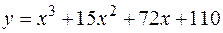 на отрезке
на отрезке 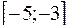 .
.
5. Найти частные производные первого порядка функции 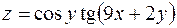 .
.
6. Найти дифференциал второго порядка функции 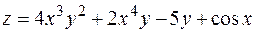 .
.
7. Найти градиент и производную функции 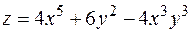 в точке
в точке 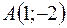 по направлению вектора
по направлению вектора 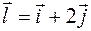 .
.
8. Найти экстремумы функции 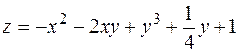 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 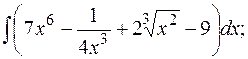
б) 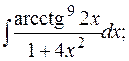
в) 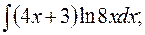
г) 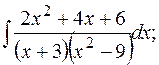
д) 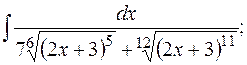
е) 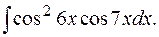
2. Найти площадь фигуры, ограниченной линиями 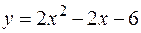 ,
, 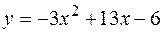 .
.
3. Найти объем тела, образованного вращением вокруг оси  фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 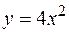 , прямой
, прямой 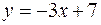 и осью
и осью 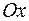 .
.
4. Записать двойной интеграл 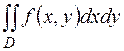 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 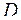 ограничена линиями
ограничена линиями 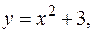
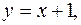
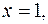 осью
осью 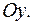
5. Найти массу пластинки, ограниченной линиями 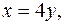
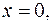
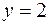 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 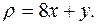
ВАРИАНТ 9
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 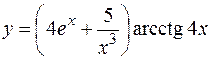 ;
;
б) 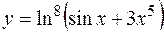 ;
;
в) 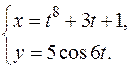
2. Найти производную второго порядка для функции 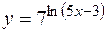 .
.
3. Исследовать функцию 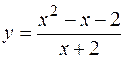 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 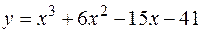 на отрезке
на отрезке 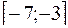 .
.
5. Найти частные производные первого порядка функции 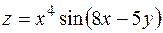 .
.
6. Найти дифференциал второго порядка функции 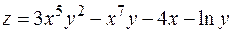 .
.
7. Найти градиент и производную функции 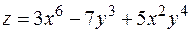 в точке
в точке 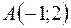 по направлению вектора
по направлению вектора 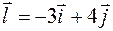 .
.
8. Найти экстремумы функции 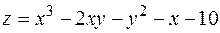 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 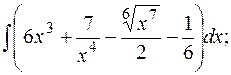
б) 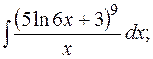
в) 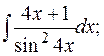
г) 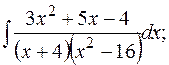
д) 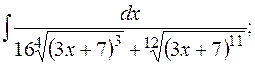
е) 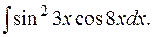
2. Найти площадь фигуры, ограниченной линиями 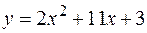 ,
, 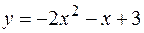 .
.
3. Найти объем тела, образованного вращением вокруг оси 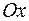 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 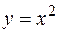 , прямой
, прямой 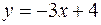 и осью
и осью 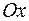 .
.
4. Записать двойной интеграл 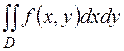 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 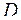 ограничена линиями
ограничена линиями 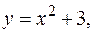
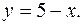
5. Найти массу пластинки, ограниченной линиями 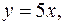
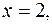
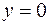 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 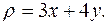
ВАРИАНТ 0
Контрольная работа №3
1. Найти производные первого порядка для заданных функций:
а) 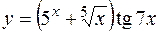 ;
;
б) 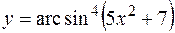 ;
;
в) 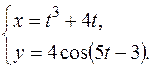
2. Найти производную второго порядка для функции 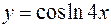 .
.
3. Исследовать функцию 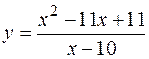 и построить ее график.
и построить ее график.
4. Найти наименьшее и наибольшее значения функции 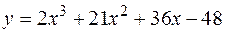 на отрезке
на отрезке 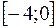 .
.
5. Найти частные производные первого порядка функции 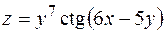 .
.
6. Найти дифференциал второго порядка функции 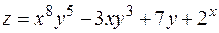 .
.
7. Найти градиент и производную функции 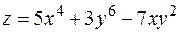 в точке
в точке 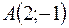 по направлению вектора
по направлению вектора 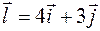 .
.
8. Найти экстремумы функции 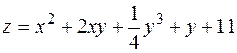 .
.
Контрольная работа №4
1. Найти неопределенные интегралы:
а) 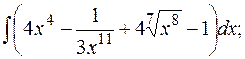
б) 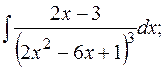
в) 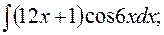
г) 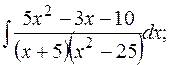
д) 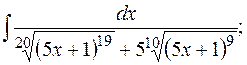
е) 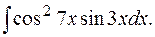
2. Найти площадь фигуры, ограниченной линиями 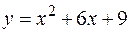 ,
, 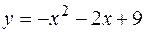 .
.
3. Найти объем тела, образованного вращением вокруг оси 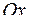 фигуры, расположенной в первой четверти и ограниченной параболой
фигуры, расположенной в первой четверти и ограниченной параболой 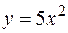 , прямой
, прямой 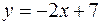 и осью
и осью 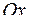 .
.
4. Записать двойной интеграл 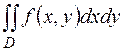 в виде повторного интеграла двумя способами, если область интегрирования
в виде повторного интеграла двумя способами, если область интегрирования 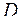 ограничена линиями
ограничена линиями 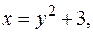
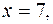
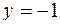 .
.
5. Найти массу пластинки, ограниченной линиями 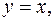
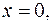
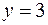 и имеющей переменную поверхностную плотность
и имеющей переменную поверхностную плотность 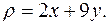
Математика: методические указания к изучению дисциплины для студентов заочной формы обучения направлений подготовки 151900 «Конструкторско-технологическое обеспечение машино-строительных производств» и 150700 «Машиностроение» (II семестр). – Брянск: БГТУ, 2013. – 43 с.
Екатерина Сергеевна Золотухина
Андрей Иванович Гореленков
Научный редактор В.М. Кобзев
Редактор издательства Л.И. Афонина
Компьютерный набор Е.С. Золотухина
Темплан 2013 г., п. 119
Подписано в печать Формат 60х84 1/16 Бумага офсетная
Офсетная печать. Печ. л. 2,32 Уч.-изд. л. 2,32 Т. 30 экз. Заказ
Издательство Брянского государственного технического университета
Брянск, бульвар 50-летия Октября, 7. тел. 58-82-49
Лаборатория оперативной печати БГТУ, ул. Институтская, 16.
УТВЕРЖДАЮ
Ректор университета
__________ О.Н. Федонин
«___»____________2013г.
МАТЕМАТИКА
Методические указания к изучению дисциплины
для студентов заочной формы обучения направлений подготовки
151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение»
(II семестр)
Брянск 2013
УДК 511
Математика [Текст]+[Электронный ресурс]: методические указания к изучению дисциплины для студентов заочной формы обучения направлений подготовки 151900 «Конструкторско-технологическое обеспечение машиностроительных производств» и 150700 «Машиностроение» (II семестр). – Брянск: БГТУ, 2013. – 43 с.
Разработали: Е.С. Золотухина, канд. физ.-мат. наук, доц.;
А.И. Горелёнков, канд. техн. наук, доц.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол №3 от 19.11.12)
ПРЕДИСЛОВИЕ
Настоящие МУ предназначены для оказания помощи студентам при изучении дисциплины «Математика» во втором семестре. Они содержат список рекомендуемой литературы, методические рекомендации к изучению тем курса и выполнению контрольных работ и задачи для контрольных работ.
По дисциплине «Математика» студенты во втором семестре сдают экзамен после выполнения предусмотренных учебным планом двух контрольных работ. Задания к ним приводятся в данных указаниях. При выполнении работ и их оформлении следует придерживаться следующих правил:
– студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки;
– работа должна быть выполнена в тетради, имеющей поля для замечаний рецензента;
– перед решением каждой задачи нужно привести полностью ее условие;
– следует придерживаться той последовательности при решении задач, в какой они даны в задании;
– на обложке тетради указываются наименование учебной дисциплины, номер контрольной работы, фамилия, имя, отчество (полностью) студента, номер его группы и зачетной книжки, фамилия, имя, отчество рецензента.
Список рекомендуемой литературы
1. Пискунов, Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Интеграл-Пресс, 2004. – Т. 1. – 416 с.
2. Пискунов, Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. – М.: Интеграл-Пресс, 2001. – Т. 2. – 544 с.
3. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1. − 288 с.
4. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 2. − 254 с.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ ТЕМ КУРСА И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Тема 1. Дифференциальное исчисление функции одной переменной
Определение производной; ее механический и геометрический смыслы. Производные суммы, разности, произведения и частного функций. Производная сложной функции. Таблица производных [3, §20]. Дифференцирование параметрически заданных функций [3, §21]. Производные высших порядков [3, §23]. Дифференциал функции [3, §24].
Пример 1.  Найти производные первого порядка для заданных функций:
Найти производные первого порядка для заданных функций:
а) 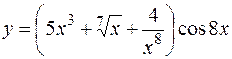 ; б)
; б) 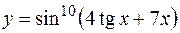 ; в)
; в) 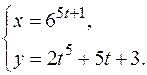
Решение. В пунктах а), б) последовательно применяем правила и формулы дифференцирования:
а) 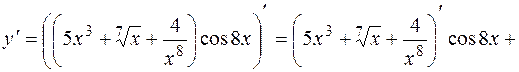
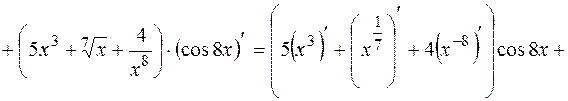
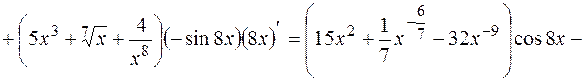
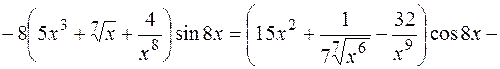
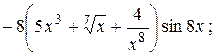
б) 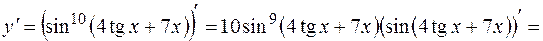
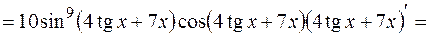
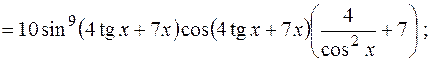
в) в данном случае заданная функция определена параметрически функциями 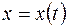 и
и 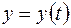 . Для нахождения производной первого порядка используем формулу
. Для нахождения производной первого порядка используем формулу 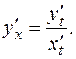
Так как 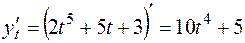 и
и 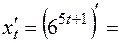
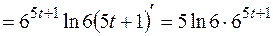 ,
,
то 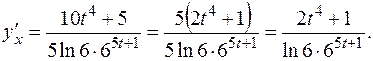
Пример 2. Найти производную второго порядка для функции 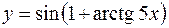 .
.
Решение. Сначала найдем производную первого порядка:
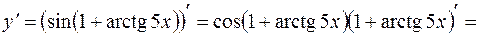
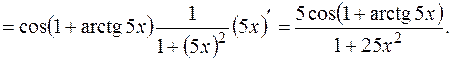
Тогда 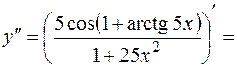
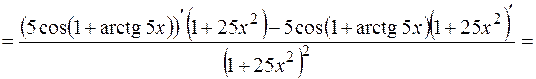
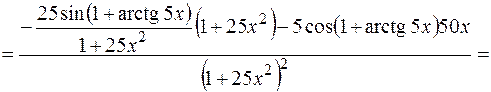
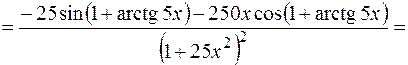
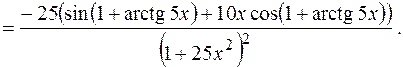
Дата: 2019-02-25, просмотров: 379.