Основные теоремы дифференциального исчисления. Правило Лопиталя. Возрастание и убывание функций. Максимум и минимум функций. Наибольшее и наименьшее значения функции на отрезке. Выпуклость графика функции. Точки перегиба. Асимптоты графика функции. Общая схема исследования функции и построения графика [3, §25].
Пример 3. Исследовать функцию 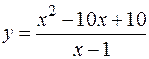 и построить ее график.
и построить ее график.
Решение.
1. Найдем область определения функции: 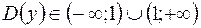 .
.
2. Заданная функция непериодическая.
3. Исследуем функцию на четность, нечетность.
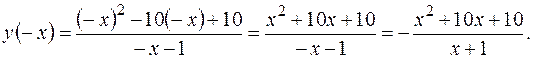
Так как 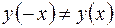 и
и 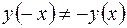 , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
4. Исследуем функцию на непрерывность.
Заданная функция является непрерывной на области определения. Точка 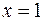 является точкой разрыва.
является точкой разрыва.
Найдем односторонние пределы функции в этой точке:
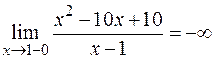 и
и 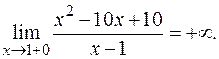
Следовательно, 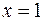 – точка разрыва II рода.
– точка разрыва II рода.
5. Исследуем функцию на экстремум и промежутки возрастания и убывания.
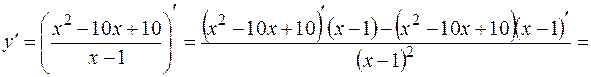
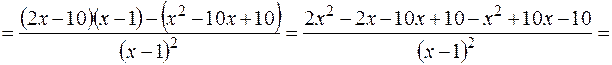
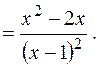
Найдем критические точки I рода:
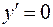 :
: 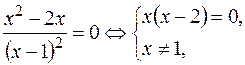 откуда
откуда 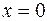 ,
, 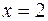 .
.
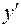 не существует в точке
не существует в точке 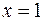 , но эта точка не принадлежит области определения функции.
, но эта точка не принадлежит области определения функции.
Значит, 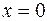 ,
, 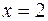 – точки возможного экстремума. Они разбивают числовую прямую на четыре промежутка. На каждом из них найдем знаки производной
– точки возможного экстремума. Они разбивают числовую прямую на четыре промежутка. На каждом из них найдем знаки производной 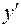 :
:
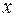
| 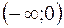
| 0 | 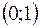
| 1 | 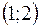
| 2 | 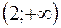
|
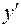
| + | 0 | – | не сущ. | – | 0 | + |
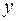
| 
| max | 
| не сущ. | 
| min | 
|
Так как при переходе через точку 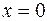 производная
производная 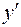 меняет знак с «+» на «–», то
меняет знак с «+» на «–», то 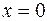 – точка максимума, тогда
– точка максимума, тогда 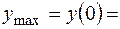
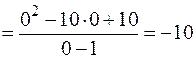 . Так как при переходе через точку
. Так как при переходе через точку 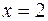 производная
производная 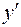 меняет знак с «–» на «+», то
меняет знак с «–» на «+», то 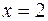 – точка минимума, тогда
– точка минимума, тогда 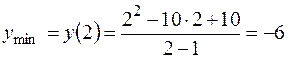 .
.
Функция возрастает при 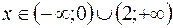 , так как на этом промежутке
, так как на этом промежутке 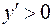 . Функция убывает при
. Функция убывает при 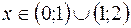 , так как на этом промежутке
, так как на этом промежутке 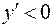 .
.
6. Исследуем график функции на выпуклость, вогнутость, точки перегиба.
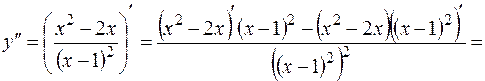
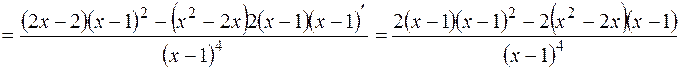
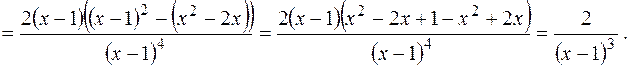
Найдем критические точки II рода:
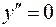 : таких точек нет;
: таких точек нет; 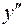 не существует в точке
не существует в точке 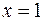 , но эта точка не принадлежит области определения функции.
, но эта точка не принадлежит области определения функции.
Значит, критических точек II рода нет, и, следовательно, нет точек перегиба.
Определим знаки второй производной:
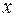
| 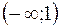
| 1 | 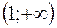
|
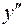
| – | не сущ. | + |
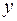
| 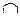
| не сущ. | 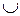
|
При 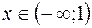 график функции является выпуклым, так как на этом промежутке
график функции является выпуклым, так как на этом промежутке 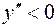 ; при
; при 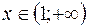 график функции является вогнутым, так как на этом промежутке
график функции является вогнутым, так как на этом промежутке 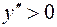 .
.
7. Исследуем график функции на наличие асимптот.
Найдем вертикальные асимптоты.
Так как 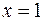 – точка разрыва II рода, то
– точка разрыва II рода, то 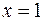 – уравнение вертикальной асимптоты.
– уравнение вертикальной асимптоты.
Найдем уравнения горизонтальных асимптот.
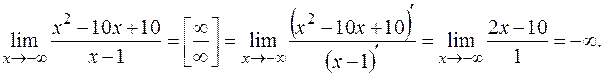
Аналогично 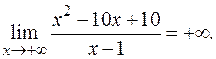
Значит, горизонтальных асимптот график функции не имеет.
Найдем уравнения наклонных асимптот графика функции в виде 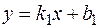 и
и 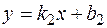 , где
, где 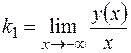 ;
; 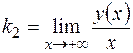 ;
; 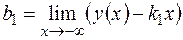 ;
; 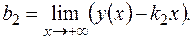
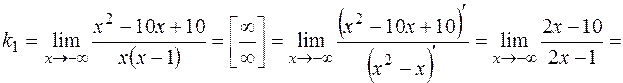
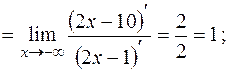
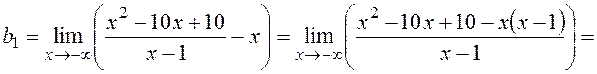
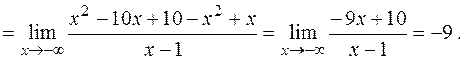
Аналогично
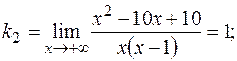
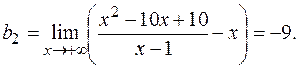
Следовательно, уравнение наклонной асимптоты имеет вид 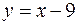 .
.
8. Найдем точки пересечения графика функции с осью 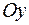 .
.
Так как 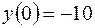 , то
, то 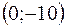 – точка пересечения с осью
– точка пересечения с осью 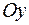 .
.
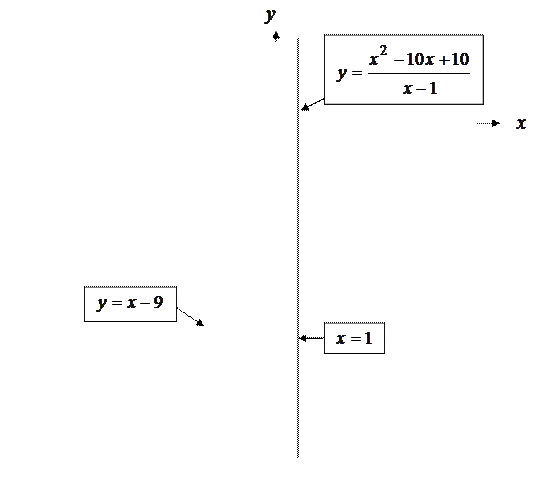
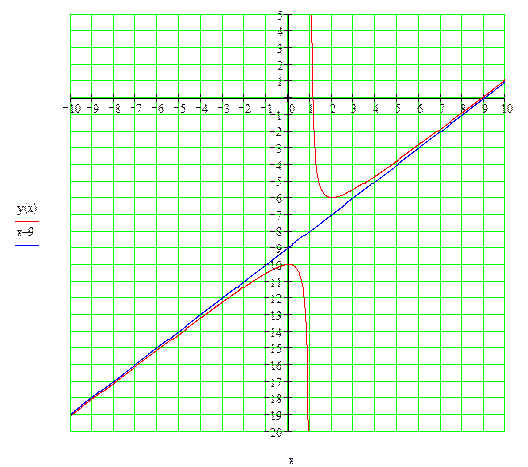
По результатам исследования построим график заданной функции.
 |

Пример 4. Найти наименьшее и наибольшее значения функции 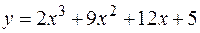 на отрезке
на отрезке 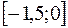 .
.
Решение.
Область определения заданной функции 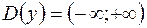 .
.
Найдем критические точки I рода, принадлежащие отрезку 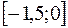 , и значения заданной функции в этих точках.
, и значения заданной функции в этих точках.
Для этого найдем производную первого порядка:
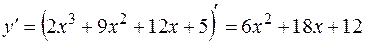 ;
;
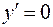 :
: 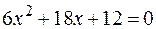 или
или 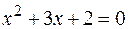 ,
, 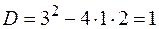 ,
, 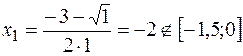 ,
, 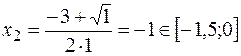 .
.
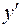 не существует: таких точек нет.
не существует: таких точек нет.
Таким образом, 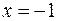 – критическая точка, принадлежащая отрезку
– критическая точка, принадлежащая отрезку 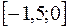 .
.
Тогда 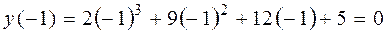 .
.
Найдем значения функции на концах отрезка:
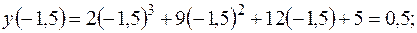
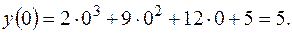
Выберем из найденных значений функции наименьшее и наибольшее: 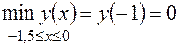 ,
, 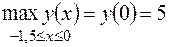 .
.
Дата: 2019-02-25, просмотров: 317.