Принцип измерения периода гармонического сигнала цифровым методом с помощью цифрового частотомера поясняется рис. 8, где приведены структурная схема устройства в режиме измерения периода гармонического колебания и соответствующие его работе временные диаграммы. Измерение интервала времени Тх цифровым методом основано на заполнении его импульсами, следующими с образцовым периодом Т0, и подсчете числа Мх этих импульсов.
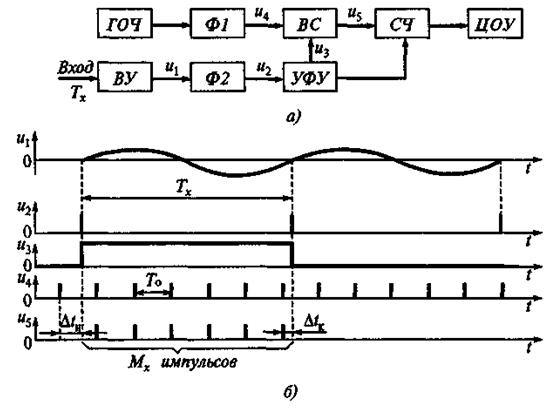
Рисунок 8 – Цифровой частотомер в режиме измерения периода (интервала времени): а) структурная схема, б) временные диаграммы
Все элементы устройства и их действие были проанализированы в предыдущем разделе. Структурный состав генератора опорной частоты при измерении периода рассматривается ниже.
Гармонический сигнал, период Тх которого требуется измерить, после прохождения входного устройства ВУ (u1 — выходной сигнал ВУ) и формирователя импульсов Ф2 преобразуется в последовательность коротких импульсов u2 с аналогичным периодом. В устройстве формирования и управления УФУ из них формируется строб-импульс u3 прямоугольной формы и длительностью Тx поступающий на один из входов временного селектора ВС. На второй вход этого селектора подаются короткие импульсы u4 с образцовым периодом следования Т0, созданные формирователем Ф1 из колебаний генератора опорной частоты ГОЧ.
Временной селектор ВС пропускает на счетчик СЧ Мx счетных импульсов u4 в течение времени Tx, равном длительности строб-импульса u3.
Измеряемый период Тx,, как следует из рис. 8, б,
Tx = MxT0 + Δtд (7)
где Δtд = Δtн - Δtκ — общая погрешность дискретизации; Δtн и δtk — погрешности дискретизации начала и конца периода Тх.
Без учета в формуле (7) погрешности Δtд число импульсов, поступившее на счетчик, Мх= Tx/T0, а измеряемый период пропорционален Мх:
Tx = MxT0 (8)
Выходной код счетчика СЧ, выдаваемый на цифровое отсчетное устройство ЦОУ, соответствует числу подсчитанных им счетных импульсов Мx , а показания ЦОУ— периоду Тх, поскольку период следования счетных импульсов u5 выбирается из соотношения T0 = 10-n, где n — целое число. Так, например, при n = 6 ЦОУ отображает число Мx , соответствующее периоду Tx , выраженному в мкс.
Погрешность измерения периода Tx , как и при измерении частоты, имеет систематическую и случайную составляющие.
Систематическая составляющая зависит от стабильности δкв образцовой частоты ГОЧ (его кварцевого генератора), а случайная определяется в основном погрешностью дискретизации Δtд. Максимальное значение этой погрешности удобно учитывать через эквивалентное изменение числа счетных импульсов Мx на ±1. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью двух значений периода Tx, получаемых по формуле (8) при Мx±1 и Мx , и равна ΔTx = ±Т0 . Соответствующая максимальная относительная погрешность δ = ±ΔTx /Tx= ±1/Mx = ±1/(Txf0), где f0 = 1/T0 — значение образцовой частоты генератора ГОЧ.
На погрешность измерения влияют также шумы в каналах формирования строб-импульса u3 и счетных импульсов u4 (рис. 8, а), вносящие в их положение временную модуляцию по случайному закону. Однако в реальных приборах с большим отношением сигнал/шум погрешность измерения за счет влияния шума пренебрежимо мала по сравнению с погрешностью дискретизации.
Суммарная относительная погрешность измерения периода определяется в процентах по формуле
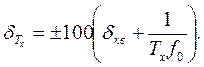(9)
Из выражения (9) следует, что из-за погрешности дискретизации погрешность измерения периода Тх резко увеличивается при его уменьшении Повышения точности измерений можно добиться за счет увеличения частоты f0 генератора ГОЧ (путем умножения частоты его кварцевого генератора в Ку раз), т.е. за счет увеличения числа счетных импульсов Мх. С этой же целью в схему после входного устройства вводят делитель частоты исследуемого сигнала с коэффициентом деления К (на рис. 8, а не показан). При этом выполняется измерение К периодов Tx и в К раз уменьшается относительная погрешность дискретизации.
Погрешность дискретизации можно уменьшить и способом измерений с многократными наблюдениями. Однако при этом значительно увеличивается время измерений. В связи с этим разработаны методы, уменьшающие погрешность дискретизации с существенно меньшим увеличением времени измерения. К их числу относится нони-усный метод, а также метод интерполяции.
Метод интерполяции состоит в том, что помимо целого числа периодов счетных импульсов, заполняющих измеряемый интервал времени, учитываются и дробные части периода, заключенные между опорным и первым счетным импульсами, а также между последним счетным импульсом и интервальным.
Измерение временных интервалов методом интерполяции поясняет рис. 9. Пусть измеряется интервал времени Tx, начало и конец которого заданы двумя импульсами uн , и иk , соответственно (рис. 9, а). Предполагается, что начало измеряемого интервала не связано синхронно со счетными импульсами, приведенными на рис. 9, а, б.
Для уменьшения составляющих погрешности дискретизации (ΔtΗ и Δtκ) в начале и конце интервала Tx, соответствующие данным погрешностям, интервалы расширяют в К раз и каждый измеряют, заполняя счетными импульсами. Учитывая погрешности расширителей, на практике расширяют интервалы большей длительности, например интервалы Δti = 2Т„ - ΔίΗ и τ2 = 2Т0 - Δ/κ (рис. 9, в). Расширители строят, используя обычно способ заряда и разряда конденсатора с разной скоростью.
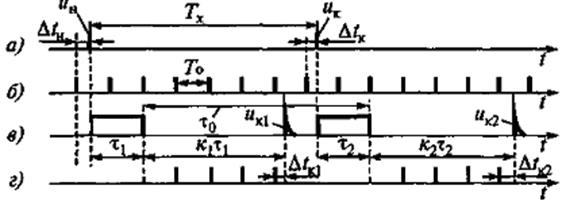
Рисунок 9 - Измерение временного интервала методом интерполяции:
а – измеряемый интервал, б – счетные импульсы, в – выходные импульсы расширителей, г – группы счетных импульсов, отражающих расширенные интервалы
На рис. 9, в приведены выходные импульсы расширителей uk1 и uк2, определяющие конец расширенных интервалов, а собственно расширенные интервалы обозначены через κ1τ1 и κ2τ2..
Расширенные интервалы, а также интервал τ0 между концами импульсов τ1 и τ2 измеряют цифровым методом, используя каналы, содержащие временной селектор и счетчик. Счетные импульсы, поступившие на вход каждого счетчика при измерении расширенных интервалов, показаны на рис. 9, г. Измеряемые интервалы, как следует из рис.9, можно представить в виде
κ1τ1 = N1T0+ Δtk1 ; κ2τ2 = N2T0+ Δtk2 ; τ0 = N0T0 (10)
где k1 и k2 — коэффициенты расширения; Ν0 , Ν1 и Ν2 — числа счетных импульсов, заполнивших отмеченные интервалы, а Δtk1 и Δtκ2 — погрешности дискретизации измерения расширенных интервалов.
Из рис. 9 также видно, что искомый интервал Тх = τ0+ τ1 - τ2. Подставляя в это выражение параметры τ0, τ1 и τ2, вычисляемые по (10), находим, что
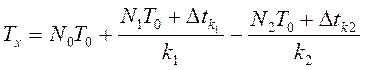(11)
При идентичности коэффициентов расширения (k1 = k2 = k), получим
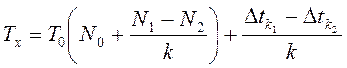(12)
Погрешности дискретизации Δtκ1 и Δtκ2 имеют равномерное распределение с пределами 0...T0, а их разность Δtκ1 - Δtκ2 распределена по треугольному закону с пределами ±T0. Поэтому максимальная погрешность дискретизации при измерении интервала T равна T0/k и уменьшается по мере роста коэффициента расширения k. Однако на практике данный коэффициент выбирают равным 128 или 256, так как при его дальнейшем увеличении существенно возрастает погрешность расширителей интервалов.
В заключение отметим, что современные точные измерительные приборы, построенные с использованием микропроцессоров, выполняют функции измерения интервалов времени и частоты на единой основе. Последнее связано с формированием и последующим измерением интервала времени, равного измеряемому интервалу (при измерении времени) или целому числу периодов измеряемого сигнала (при измерении периода и частоты). Сформированный подобным путем интервал измеряется цифровым методом с применением описанного выше метода с интерполяцией для уменьшения погрешности дискретизации.
В таких приборах при измерении расширенных интервалов (k1τ1 и k2τ2) и интервала τ0 (рис. 9) соответствующие числа счетных импульсов (Ν1, Ν2 и n0), заполняющих эти интервалы, накапливаются в отдельных регистрах.
Длительность Тх одиночного интервала вычисляется микропроцессором согласно формуле
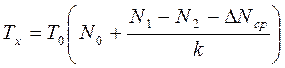, (13)
где ΔNср — поправочное число, учитывающее взаимное рассогласование расширителей и определяемое в процессе их автоматической калибровки с помощью микропроцессора.
При измерении повторяющихся интервалов (с усреднением) дополнительно подсчитывается число NE усредненных за время измерения интервалов. В этом случае интервал времени вычисляется согласно выражению
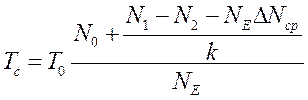(14)
В случае измерения периода Т число NE является количеством усредняемых периодов. При этом период вычисляется по формуле
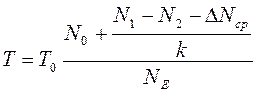(15)
Заключение
В заключительной части лекции подводится итог занятия и делается вывод о достижении цели занятия.
Контрольные вопросы
1. Дайте определение частоты, периода и интервала времени электрического сигнала. Основные измерительные приборы частоты и интервалов времени.
2. Поясните сущность и дайте характеристику методов измерения частоты путем сравнения с частотой источника образцовых колебаний (резонансный и с помощью осциллографа).
3. Поясните сущность и дайте характеристику гетеродинного метода измерения частоты.
4. Поясните сущность и дайте характеристику метода измерения частоты способом заряда и разряда конденсатора.
5. Поясните сущность и дайте характеристику цифрового метода измерения частоты.
6. Поясните сущность и дайте характеристику цифрового метода измерения интервалов времени.
ЗАДАНИЕ СТУДЕНТАМ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Рассмотреть и законспектировать основные руководящие документы по метрологии в вопросах стандартизации частоты.
2. Самостоятельно рассмотреть эталоны и эталонные средства измерений частоты.
ЛИТЕРАТУРА
Основная литература:
1. Метрология и радиоизмерения. Учебник для вузов/ В.И. Нефедов, В.И. Хахин, В.К. Битюков и др./Под ред. профессора В.И. Нефедова. – М.: Высшая школа, 2011. – 526 с.
2. Метрология и электрорадиоизмерения в телекоммуникационных системах/ В.И. Нефедов, В.И. Хахин, В.К. Битюков и др /Под ред. профессора В.И. Нефедова. – М.: Высшая школа, 2010. – 340 с.
Дополнительная литература:
3. Никифоров А.Д., Бакиев Т.А. Метрология, стандартизация и сертификация. – М.: Высшая школа, 2006. – 240 с.
4. Снытников А.А. Лицензирование и сертификация в области защиты информации. – М.: Гелиос АРВ, 2005. – 192 с.
5. Лаптиев Э. И., Брюхонов В. А. Межрегиональная научно-практическая конференция "Метрологическое обеспечение испытаний и сертификации продукции и услуг" // Стандарты и качество, 2008г., №8, стр. 26-28.
6. Стандартизация и управление качеством продукции: Учебник для ВУЗов / В. А. Швандар, В. Пейджер: Панов, Е. М. Купряков и др.; под ред. В. А. Швандара. - М.: Юнити-Дана, 2009. - 487 с.
7. Шишкин И. Ф. Метрология, стандартизация и управление качеством. - М.: Издательство стандартов, 2007. - 342 с.
Дата: 2019-02-25, просмотров: 315.
