Гетеродинный метод является одной из разновидностей методов сравнения измеряемой частоты f_х с частотой эталонного генератора f_кв (аналог метода нулевых биений); в качестве последнего используется ге­теродин. Упрощенная структурная схема гетеродинного частотомера представлена на рис. 8. Она содержит: входное устройство, кварцевый генератор, смеситель, гетеродин, усилитель низкой частоты и индикатор (нулевых биений).

Действие гетеродинного частотомера сводится к следующему про­стому принципу: при переключении ключа К в положение 1 производит­ся корректировка шкалы гетеродина; при положении 2 — измерение частоты, подаваемой на входное устройство.

Корректировка шкалы гетеродина (ключ К находится в положении 1) осуществляется непосредственно перед проведением измерения с помо­щью дополнительного, кварцевого генератора. Сигнал, поступающий с кварцевого генератора, имеет сложную форму и содержит ряд гармонических составляющих с кратными частотами: f_кв1,f_кв2,...,f_квi ..., f_квn,  где n — номер гармоники. Частоты этих гармоник кварцевого генератора в радиотехнике называются кварцевыми точками.

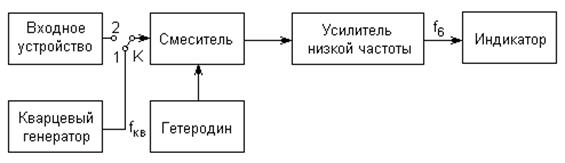
Рисунок 8 - Упрощенная структурная схема гетеродинного частотомера

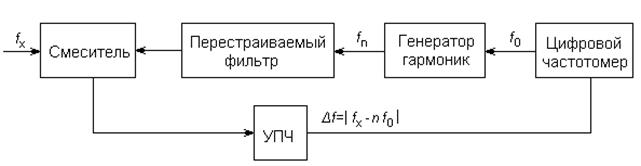
Рисунок 9 - Структурная схема дискретного гетеродинного преобразователя

При измерениях отсчетный лимб гетеродина устанавливают в поло­жение, соответствующее ближайшей к измеряемой частоте f_x кварцевой точке (примерное значение измеряемой частоты должно быть известно, иначе процесс измерения очень усложняется). Поскольку измеряемый и гетеродинный сигналы поступают на смеситель, на его выходе возника­ют колебания с суммарными, разностными и комбинационными частотами. Индикаторный прибор фиксирует наличие сигнала биений на минимальной разностной частоте f₆ = |f_квi-f_r|, проходящего через уси­литель низкой частоты (высокочастотные составляющие, получающиеся в результате смешения частот кварцевого генератора и гетеродина, через усилитель низкой частоты не проходят). Меняя емкость в контуре гете­родина, получают нулевые биения, следовательно, частота гетеродина становится равной частоте кварцевой гармоники f_r ≈ f_квi

После этого приступают к измерению неизвестной частоты f_x, пере­водя ключ К в положение 2. Вращая отсчетный лимб гетеродина, доби­ваются нулевых биений и по откорректированной шкале гетеродина оп­ределяют значение f_x ≈ f_r..

Гетеродинные частотомеры являются достаточно точными измери­тельными приборами. Их относительная погрешность измерения лежит в пределах 10³...10⁵. Однако в диапазоне средних частот (до 200 МГц и ниже) они вытесняются электронно-счетными частотомерами, которые обеспечивают ту же высокую точность, но значительно проще в экс­плуатации.

В диапазоне СВЧ гетеродинный метод измерения применяется совме­стно с электронно-счетными (цифровыми) методами. Расширение преде­ла измерения до 10... 12 ГГц достигается за счет переноса (преобра­зования) измеряемой частоты в область более низких частот. Такой пе­ренос можно осуществить, например, с помощью дискретного гетеро­динного преобразователя частоты, структурная схема которого приве­дена на рис. 7.6 вместе с цифровым частотомером.

В составе цифрового частотомера содержится генератор опорной (эталонной, образцовой) частоты f₀. Эта частота поступает на нелиней­ный элемент (генератор гармоник), который формирует сетку гармонических составляющих f_n=nf₀, где n — целые числа. С помощью пере­страиваемого фильтра (обычно это объемный резонатор со шкалой) до­биваются выделения из них гармоники f_n, ближайшей к измеряемой частоте f_x. При этом на выходе смесителя устройства появляется сигнал с разностной частотой F=|nf₀-f_x|.

Усилитель промежуточной частоты (УПЧ) имеет полосу пропуска­ния, несколько большую опорной частоты f₀. Поэтому он усиливает сиг­нал с разностной частотой F < f₀, измеряемой далее цифровым частото­мером.

Результат измерения неизвестной частоты f_x вычисляют по формуле f_x = nf₀ ± F, в которой n — номер гармоники, считываемой со шкалы пе­рестраиваемого фильтра. Поскольку это выражение неоднозначно, то для получения правильного результата проводят второе измерение, вы­бирая с помощью перестраиваемого фильтра гармонику (n ± 1)f₀, сосед­нюю с гармоникой nf₀. Если результаты вычисления частоты f_А совпали при двух измерениях, то они верны.