Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения

Если система ограничений задачи линейного программирования включает неравенство и уравнение, то задача называется общей задачей линейного программирования, а если только уравнение – то основной задачи линейного программирования (ОЗЛП).

Основная задача линейного программирования заключается в следующем:

Найти неотрицательное значение переменных х₁, х₂, … , х_n , удовлетворяющих “m” условиям - равенства:

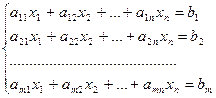
и обращающих в max(min) целевую функцию:

F=C₁X₁+C₂X₂+…+C_nX_n→max (min)

x_j≥0 ( )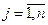

Если отыскивается мах функции, то задача линейного программирования называется задачей максимизации, а если min , то задачей минимизации

Задача минимизации легко сводится к задачи максимизации путем замены знаков коэффициентов целевой функции на противоположные.

Допустимым решением основной задачи линейного программирования называют всякую совокупность неотрицательных значений х₁, х₂, x_n , удовлетворяющих системе ограничений.

Оптимальным называют то из допустимых решений, которое обращает в max(min) целевую функцию.

Всякая общая задача линейного программирования может быть сведена к равносильной ей основной задаче путем введения новых неизвестных, называемых дополнительными неизвестные. Переменные, которые входят в ограничения исходной задачи, называется основными

В неравенствах типа «<=» к левым частям неравенств прибавляются дополнительные переменные, а в неравенствах типа «>=» из левых частей неравенств вычитаются дополнительные переменные.

Число дополнительных переменных равно числу ограничений - неравенств.

В целевую функцию все дополнительные переменные входят с нулевыми коэффициентами.

В этом случае система ограничений должна быть задана только в виде неравенств.

Решение начинается с построения многоугольника допустимых решений, который строится в декартовой системе координат. Стороны этого многоугольника располагаются на прямых, уравнения которых получаются, если в системе неравенств знаки неравенств заменить на точное равенство. Сам многоугольник есть пересечение полуплоскостей, на которые делит плоскость каждая из указанных прямых.

Чтобы определить нужную полуплоскость, подставляют координаты какой- либо точки (чаще всего начало координат) в левую часть неравенства. Если условие неравенства выполняется, то область решения задачи включает выбранную точку , в противном случае , искомая полуплоскость располагается по другую сторону граничной прямой.

Любая точка этого многоугольника, как внутри его, так и по контуру ,будет удовлетворять заданной системе ограничений, т.е имеем бесчисленное множество допустимых решений. Очевидно, оптимальное решение задачи будет в одной из вершин многоугольника допустимых решений.

Чтобы определить оптимальное решение, необходимо:

- построить вектор целевой функции. Его начало лежит в начале координат, а конец определяется коэффициентами целевой функции;

- провести прямую, перпендикулярную вектору и проходящую через начало координат (линию наклона целевой функции);

- переместить линию наклона целевой функции параллельно самой себе в направлении вектора, если требуется найти max, и в противоположном направлении, если требуется найти min, до тех пор, пока она не сместится в область недопустимых значений (пока она не будет пересекать многоугольник) и определить точку оптимума.

- выяснить, на пересечении каких прямых лежит эта точка, составить из них систему уравнений, решить её и найти координаты точки оптимума, а затем подставить их в целевую функцию и вычислить ее оптимальное значение.