В отличие от обычной формы закона Ома, в комплексной форме напряжение, токи, сопротивления и ЭДС записываются как комплексные числа. Данное нововведение основано на том, что в цепях переменного тока существуют активные и реактивные значения напряжений, токов и сопротивлений, что требует определённых корректив.

Итак, вместо активного сопротивления R, которое используется в основном в цепях постоянного тока, запишем полное (комплексное) сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже становятся комплексными величинами. При практических расчётах удобнее пользоваться действующими значениями.

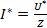, Z-комплексное (полное) сопротивление (импеданс)

Z= 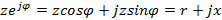, r-активное сопротивление, x-реактивное сопротивление, z-полное сопротивление,j=i=комплексная единица

17. ПО ПРАКТИКЕ

Решение синусоидальных цепей: 1. Закон Ома в комплексной форме. Необходимо помнить, что при последовательном соединении I1=I2=Ioбщ, U1+U2=Uобщ, а при параллельном U1=U2=Uобщ, I1+I2=Iобщ

18. Уравнения Максвелла в интегральной и дифференциальной форме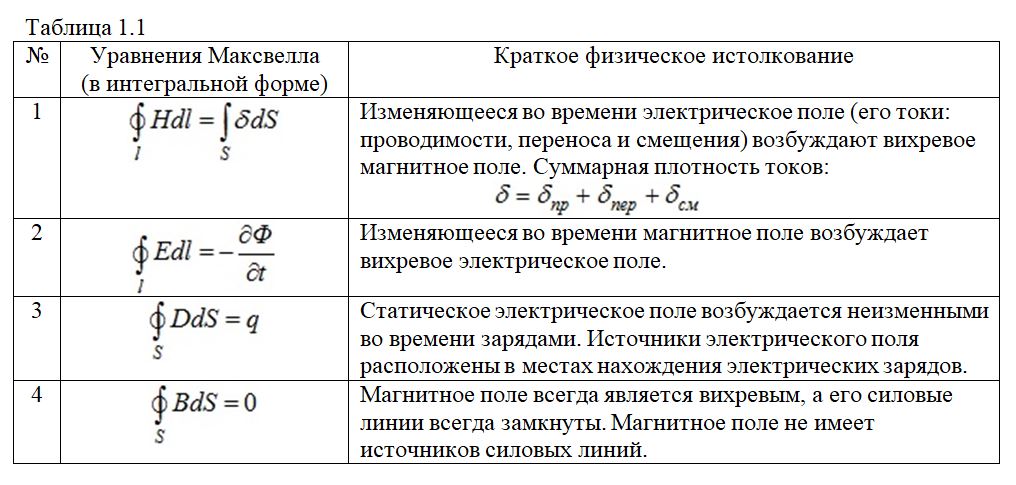

Б/Н: Циркуляцией МП называется интеграл по замкнутому контуру от скалярного произведения индукции МП на элемент контура/ Векторная сумма магнитной индукции, направленная по касательной к линиям магнитного поля.

Градиент – векторная производная скалярного поля

Дивергенция – скалярная производная векторная поля, выражает насколько в данной точке поле расходится. Ротор – векторная производная векторного поля, показывает, насколько поле закручено.

Теорема Стокса – интегрирование вект.поля и дифф.вект.поля. Циркуляция векторного поля по замкнутому положительно ориентированному контур L равна потоку ротора этого поля через любую гладкую поверхность S, опирающуюся на данный контур.

Время релаксации – время, за которое величина приближается к своему равновесному значению в е раз.

Самоиндукцией называется появление в проводнике ЭДС, направленной противоположно относительно напряжения источника питания при протекании тока. ЭДС самоиндукции прямо пропорциональна индуктивности катушки изменения силы тока в эл.цепи

ЭЛЕМЕНТАРНЫМ МАГНИТНЫМ ПОТОКОМ dФB через физически малый элемент поверхности площадью dS называется скалярное произведение вектора индукции магнитного поля B на вектор нормали n к данному элементу поверхности и на площадь

19.Вывод волнового уравнения из уравнений Максвелла

Волна – колебание, распространяющее в пространстве. Уравнение волны в общем виде

f(ωt-kx).

Система уравнений Максвелла– система, которая описывает эл-магнитные св-ва всего!

div B=0, div D=ρ, rot E=- 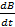, rot H=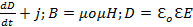

Возьмем виды среды, где нет свободных зарядов и соответственно эл.тока

j=0, ρ=0. rot (rot E)= rot (- )= =-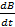

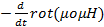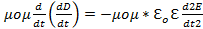
Δ= 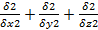 – оператор Лапласа (вторая пространственная производная)

ΔЕ= 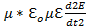– волновое уравнение

*Поглощением света называется явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии. В результате поглощения интенсивность света при прохождении через вещество уменьшается.

Поглощение света в веществе описывается законом Бугера:

I=I₀e^-αx, I, I0 – интенсивности плоской монохроматической волны на входе и выходе слоя поглощающего вещества толщиной х, α-коэффициент поглощения, зависящий от длины волны света, и не зависящий от интенсивности света.

20. Уравнение волны и смысл входящих в него величин

Если плоская волна распространяется в заданном направлении, для нее производные по другим направлениям =0

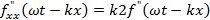
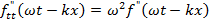
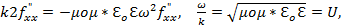 это фазовая скорость волны –скорость перемещения фазы волны в пространстве.

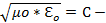свободное пространство, 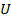=с/n , n-показатель преломления среды.

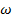 – циклическая частота колебаний, генерируемых источником, с которой колеблются и точки среды

21. Бегущие и стоящие волны.

Волна, в которой колебания частиц среды и распространение возмущения происходят в одном направлении, называется продольной.

Волна, в которой частицы среды колеблются перпендикулярно направлению распространения возмущений, называется поперечной.

Бегущая волна — волновое движение, при котором поверхность равных фаз (фазовые волновые фронты) перемещается с конечной скоростью (постоянной для однородной среды). С бегущей волной связан перенос энергии, импульса или других характеристик процесс

Бегущая волна - волна, которая при распространении в среде переносит энергию (в отличие от стоячей волны). Примеры: упругая волна в стержне, столбе газа, жидкости, электромагнитная волна вдоль длинной линии.

Бегущая волна — волновое возмущение, изменяющееся во времени t и пространстве z согласно выражению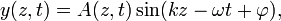

где A(z,t) — амплитудная огибающая волны, k — волновое число и фи фаза колебаний.

Стоя́чая волна́ — волна, образующаяся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.

Если навстречу друг другу распространяются две гармонические волны

S1=Acos(ωt-kх) и S2=Acos(ωt+kх), то образуется стоячая волна

S=S1+S2=2Аcoskx cosωt.

В случае стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут энергию в противоположных направлениях. Т.о. стоячая волна характеризует колебательное состояние среды.

Коэффициент стоячей волны – отношение наибольшего значения амплитуды напряжённости электрического или магнитного поля

Поскольку неравномерность распределения амплитуды волны вдоль линии обусловлена интерференцией («сложением и вычитанием») падающей и отражённой волн, то наибольшее значение амплитуды A волны вдоль линии (то есть значение амплитуды в пучности) составляет Ао + Во,

а наименьшее значение амплитуды (то есть значение амплитуды в узле) составляет

Ао — Во,

где Ао — амплитуда падающей волны, Во — амплитуда отражённой волны.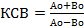

Желательно, чтобы значение КСВ в линии передачи было близко к единице, при этом максимален КПД системы «линия передачи — нагрузка», равный отношению мощности, выделяемой в нагрузке, к мощности падающей волны, отдаваемой генератором в линию передачи.

Коэфф.отражения хххх

22=19

23.Интерференция света. Оптический путь, расчет интерференционной картины. Интерференция света: При наложении световые волн в общем случае выполняется принцип суперпозиции: результирующий световой вектор является суммой световых векторов отдельных волн.

 Две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового направления, изменяющиеся по закону косинуса. Напряженности электрического и магнитного полей подчиняются принципу суперпозиции. При наложении двух (или более) когерентных волн происходит пространственное перераспределение светового потока, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга и наблюдается интерференционная картина.

Произведение геометрической длины пути световой волны на показатель преломления в этой среде называется оптической длиной пути. А разность оптических длин проходимыми двумя волнами называется оптической разностью хода.

Интерференция свойственна не только световым волнам, являющимися по своей природе электромагнитными волнами, но и волнам любого другого типа.

Методы наблюдения интерференции света.

1. Метод Юнга. Источником сета служит ярко освещенная щельSот которой световая волна падает на две узкие равноудаленные щели S1 и S2, параллельные щели S. Таким образом, щели играют роль когерентных источников. Интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии от щелей S1 и S2. В такой постановке Юнг осуществил первое наблюдение интерференции.

2. Зеркала Френеля.Два плоских зеркала расположены относительно друг друга под небольшим углом (φ=1). На расстоянииrот линии пересечения зеркал параллельно ей находится прямолинейный источник светаS. Световые пучки, отразившись от зеркал, являются мнимыми изображениями S в зеркалах. Мнимые источники S1 и S2 взаимно когерентны, и их световые пучки интерферируют в области взаимного перекрытия. От прямого попадания света на экран предохраняет заслонка.

3. Бипризма Френеля.Она состоит из двух одинаковых с общей гранью призм с малыми преломляющими углами. Свет от прямолинейного источника S преломляется в обеих призмах, в результате чего образуются две когерентные цилиндрические волны, исходящих из мнимых источников S1 и S2. На поверхности экрана в некоторой его части происходит наложение этих волн и наблюдается интерференция.

Расчет интерференционной картины включает два уравнения:

Если оптическая разность хода равна целому числу длин волн в вакууме

Δ=±mλ (m=0,1,2), то δ=±2mΠ, колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Значит интерференционный максимум

Δ=±(2m+1)λ/2 (m=0,1,2), то δ=±(2m+1)Π, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе

Расчет интерференционной картины от двух источников можно провести, используя две узкие параллельные щели, расположенные достаточно близко друг к другу. Они находятся на расстоянии d и являются когерентными. Интерференция наблюдается в произвольной точке А экрана, параллельном обеим щелям и расположенного от них на расстоянии l, большего, чем d.(Рис.251 из Трофимовой)