Пусть дан ряд (А). а_n≥0 Ɐn, члены ряда не возрастают.

a₁≥a₂≥… Ɐn

f(x) – непрерывная возрастающая положительная функция [1; +∞]

f(1)=a₁

…

f(n)=a_n

-

-

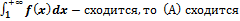
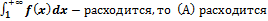
Абсолютная и условная сходимость. Теорема Коши.

Теорема Коши: если ряд, состоящий из модулей членов данного ряда, сходится, то сходится и исходный ряд.

(А) – абсолютно сходящийся, если сходится (А)*, состоящий из абсолютных величин членов данного ряда.

Если (А) – сходится, а ряд (А)* - расходится, то (А) сходится условно. Если (А)* - сходится, то (А) сходится абсолютно.

Замечание: из расходимости (А)* не следует расходимость (А), но если расходимость (А)* установлена с помощью признаков Даламбера или Коши, то 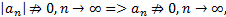 то есть из расходимости (А)*, установленной с помощью признака Даламбера или Коши, следует расходимость ряда (А).

Знакочередующиеся ряды. Теорема Лейбница.

Ряд называется знакочередующимся, если два его соседних члена являются числами разных знаков a_n*a_n+1<0

Будем предполагать, что всегда a₁>0 и будем явно выписывать знаки членов ряда, считая сами a_n>0 для любых n

a₁-a₂+a₃-…+(-1)^n-1*a_n+ … = 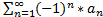       (1)

Теорема Лейбница

Если члены знакочередующегося ряда (1) по абсолютной величине монотонно убывают

1) a₁>a₂>…>a_n>…n

2) стремится к 0 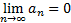, то знакочередующийся ряд (1) сходится и его сумма 0<S<a₁

Следствие

Остаток r_n ряда лейбницкого типа имеет знак своего первого члена и меньше его по абсолютной величине.

Свойства абсолютно и условно сходящихся рядов.

Пусть ряд (А): a₁+a₂+a₃+…+a_n+… = = 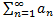 сходится и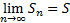

Объединим члены ряда (А) в группы произвольным образом,

получим (a₁+a_k1)+(a_k+1+…+a_k2)+…+((a_kn-1+…+a_kn)+… (*)

Теорема

Ряд (*) всегда сходится и имеет ту же самую сумму, что и данный ряд (А), т.е. сходящиеся ряды обладают сочетательными свойством.

Замечание

Эта аналогия с конечными суммами нарушается, если применить сочетательное свойство в "обратном порядке". Если (*) сходится, члены которого представляют собой суммы конечного числа членов ряда А, то опустив скобки получим ряд, который может оказаться расходящимся.

Например:

(1-1)+(1-1)+…+(1-1)+… - сходится

1-1+1-1+1-1+…+1-1+… - расходится

Теорема Дирихле

Абсолютно сходящиеся ряды обладают переместительными свойствами

Теорема Римана

Если ряд сходится условно, то путём перестановки его членов, можно получить ряд, имеющий наперёд заданную сумму, а также расходящийся ряд, т.е. условно сходящиеся ряды переместительным свойством не обладают.

Замечание

Различия между абсолютно и условно сходящимися рядами заключается в том. что условная сходимость осуществляется благодаря взаимному погашению положительных и отрицательных членов ряда и поэтому существенно зависит от того, в каком порядке члены ряда следуют друг за другом. А абсолютная сходимость основана на быстроте убывания этих членов и не зависит от порядка их следования друг за другом.