Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

у’’+P(x)y’+Q(x)y=f(x) (1)

y”+P(x)y’+Q(x)y=0 (2)

Общее решение неод ур-я (1) мб записана в виде y=u*y1(x)+v*y2(x),где y1(x);y2(x)-лнз решение однородного ур-я , а u=u(x) v=v(x) 2 спец образом подобраны ф-ции содержащие по 1-ой произв. Постоянной.

Доказательство:

Составим y=u(x)*y1(x)+v(x)*y2(x) тогда y’=u’y1+uy1+v’y2+vy2 будем искать uv такими, чтобы u’y1+v’y2=0 (3)

Тогда y’=uy1’+vy2’

y”=u’y1’+uy”+v’y2’+vy2”

Получим u’y1’+uy1”+v’y2”+vy2”+p(x)[uy1’+vy2’]+q(x)[uy1+vy2]=f(x)

u[y”+p(x)y’+q(x)y1]+v[y2”+p(x)y2’+q(x)y2]+u’y1’+v’y2’=f(x)

u’y1’+v’y2’=f(x) (4)

 

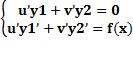
​​​(5)

Систему (5) можно рассматривать как условие на ф-цию u’v’,чтобы y=uy1+vy2 была решение ур-е(1)

Для того чтобы (5) имела E! ,чтобы опред. Этой системы дельта не равно 0

Дельта= W(y1;y2) не равно 0, любой х, тк ф-ция y1(x);y2(x) лнз

Из системы(5) можем найти u’ v’; интегрируя, найдем

u(x)=u1(x)+C1

v(x)=v1(x)+C2

Подставляя найденные знач.y=[u1(x)+C1]y1+[v1(x)+C2]y2=(C1y1+C2y2)+(u1(x)y1+v1(x)y2)

1-ое слаг. Есть y(оо) по Т4 ЛОДУ2. Ф-ция y по построению есть y(он) ур-я(1), тода по Т. о структуре решения ЛНДУ выражения во ЛНДУ 2-ой скобки есть чн ур-я(1), а тогда по Т1 y есть общее решение ур-я(1)

 

ЛОДУ с постоянными коэффициентами.

y”+Р(у’)+Q(y)=0 (1) ; P,Q — const;

Теорема 1: если k0 является корнем k^2+pk+q=0 (2) то y=e^k0x — решение (1)

Ур-е (2) — характеристическое для ЛОДУ (1)

Доказательство:

Найдем y’=k0*e^k0x

y”=k0²*e^k0x

из (1) => k0²e^k0x+P*k0*e^k0x+Q*e^k0x=e^k0x(k0²+Pk+Q)=0 => y=e^k0x — решение (1)

Теорема 2:

Общее решения (1) моджет быть написано по одной из след. Формул:

1) k1≠k2; k1,k2∈ℝ => y_oo=C1e^k1x+C2e^k2x; C1,C2 — const;

2) k1=k2; k1,k2∈ℝ => y_oo=C1e^k1x+C2xe^k2x; C1,C2 — const;

3) k1,2=α±βi, α,β∈ℝ y=e^αx(C1cosβx+C2sinβx) i²=-1;

Доказательство:

1 случай:

Пусть k1 и k2 — корни (2), k1≠k2, тогда у1=e^k1x и у2=e^k2x — решение (1) по Т1;

у1/у2=е^k1x/e^k2x=e^k1x-k2x=e^x(k1-k2) ≠const, т.к. k1≠k2 => y1 и у2 — линейно независимые => по теореме о структуре решения ЛОДУ: у_оо=С1е^k1x+C2e^k2x, C1,C2 — const.

2 случай:

k1=k2 => по Т1 y1=e^k1x – решение (1)

Рассмотрим y2=xe^k1x, покажем, что оно является решением (1):

y2’=e^k1x+xk1e^k1x

y2”=k1e^k1x+k1e^k1x+k1²xe^k1x=+k1²e^k1x

2k1e^k1x+ k1²xe^k1x+P(e^k1x+xk1e^k1x)+Q(xe^k1x)=e^k1xx(k1²+Pk1+Q)+2e^k1x(k1+P/2)

y2=xe^k1x – решение (1)

у1 и у2 – линейно независимые, т.к. у2/у1=xe^k1x/e^k1x=x≠const => y1 и у2 – линейно независимые.

По теореме о структуре решение ЛОДУ: У_оо=С1у^k1x+C2xe^k1x

3 случай:

k1=α±βi, тогда по Т1 e^(α±βi)x – решение.

e^α+βi=e^α(cosβ+isinβ) – формула Эйлера.

e^(α±βi)х=e^αх(cosβ±isinβ) – решение (1)

у1=e^αxcosβx и у2=e^αxsinβx – взятые в отдельности - решения (1)

функция у1 и у2 – линейно независимые, т.к. у2/у1=tgβx≠const

у1 и у2 – линейно независимые, тогда по теореме о структуре решения ЛОДу 2-го порядка У_оо=С1e^αxcosβx+С2e^αxsinβx или У_оо=e^αx(С1cosβx+С2sinβx)

 

ЛНДУ 2-го порядка с постоянными коэффициентами и правой частью специального вида.

y”+Py’+Qy=f(x) (1)

Рассмотрим различные правые части в уравнении (1)

1) f(x)=a_nxⁿ+…+a₁x+a₀ – линейное n-ой степени.

Решение (1) будем также искать решение в виде многочлена, подобрав в соответствующем образе его степень и коэффициенты:

а. Q≠0 => У_чн ищут в виде многочлена той же степени, что и многочлен в правой части: У_чн=b_nxⁿ+…+b₁x+b₀

От У_чн берем первую и вторую производные, чтобы найти b.

Подставляем в (1), приравниваем коэффициенты к одинаковым степеням х в левой и правой части (1). Получаем систему лин. уравнений для отыскания неизвестных буквенных коэффициентов.

b. Q=0, P≠0 => У_чн=x(b_nxⁿ+…+b₁x+b₀)

c. Q=P=0, => У_чн=xⁿ(b_nxⁿ+…+b₁x+b₀),

в случае b можно получить порядок уравнения y’=z, y”=z’;

в случае c решение ищется двукратным последовательным интегрированием.

2) f(x)=e^αx(a_nxⁿ+…+a₁x+a₀)

а . α≠k1,k2, то У_чн=e^αx(b_nxⁿ+…+b₁x+b₀)

b. α=k1 или k2 => У_чн=e^αxх(b_nxⁿ+…+b₁x+b₀)

с . α=k1=k2 => У_чн=e^αxх²(b_nxⁿ+…+b₁x+b₀)

3) f(x)=e^αx(P_n(x)cosβx+Q_m(x)sinβx)

a. α±βi≠k1,k2 => У_чн=e^αx(Т_S(х)cosβx+L_s(x)sinβx) S-наибольшая из степеней m и n.

b. α±βi=k1,k2 => У_чн=e^αx(Т_S(х)cosβx+L_s(x)sinβx)

У_он=У_оо+У_чн

Следствие:

Частное решение уравнений (их сумма) у”+Py’+Qy=f1(x) у”+Py’+Qy=f2(x) дают частное решение уравнения у”+Py’+Qy=f1(x)+f2(x)

 

Системы обыкновенных ДУ.

Системой ДУ называется совокупность, в каждое из которых входит независимая переменная, искомые функции и их производные.

Всегда предполагается, что число уравнений системы равно числу неизвестных функций.

Решением системы ДУ называется совокупность функций, при подстановке которых в каждое уравнение системы получается верное равенство.

Нормальной системой ДУ называется система уравнений вида:

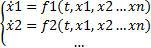(1)

Обычно нормальную систему ДУ (1) можно заменить одним ДУ, порядок которого равен числу уравнений системы.

Общее решение (1) имеет вид:

   

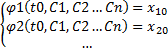
Для нормальных систем ДУ имеет место теорема, гарантирующая существование и единственность частного решения.