Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Система уравнений вида:

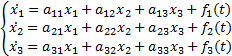 ,где х_i=х_i(t), 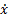_i=dx_i/dt, a_ij(i=1,2,3; j=1,2,3) – постоянные коэффициенты и f_i(t) – непрерывные функции аргумента t называется системой линейных ДУ с постоянными коэффициентами 3-го порядка (порядок равен количеству уравнений); неоднородной, если хотя бы одна из функций не равна тождественно нулю, и однородной, если все функции тождественно равны нулю.

 

Ряд и его частичные суммы. Сходящиеся и расходящиеся ряды.

Рассмотрим бесконечную последовательность чисел:

a₁, a₂… a_n= {a_n}

Числовой ряд – выражение 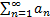 (1), которое получится, если члены последовательности {a_n} формально соединить знаком «+».

Числа а₁, а₂…а_n – члены ряда.

Выражение для n-го члена ряда при произвольном n называется общим членом ряда.

Рассмотрим суммы конечного числа членов (1)

S₁=a₁;

S₂=a₁+a₂;

…

S_n=a₁+a₂+…+a_n и т.д.

Сумма первых n слагаемых (1) – n-я частичная сумма.

Т.к. в (1) бесконечное число слагаемых, то можно составить бесконечную последовательность частичных сумм.

S₁, S₂…S_n={S_n}

Ряд (1) сходящийся, если существует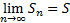

S – сумма ряда (1).

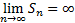Если  или 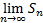 не существует, то (1) – расходящийся.

 

Основные свойства сходящихся рядов.

Ряд 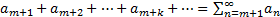, полученный из ряда a₁+…a_n=  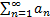(1), отбрасывание первых m слагаемых называется остатком ряда (1) после m-го члена.

Теорема 1.

Если (1) сходится, то сходится и любой из его остатков (2). И обратно, если (2) сходится, то сходится и исходный (1). Другими словами, отбрасывание в начале ряда или приписывание конечного числа слагаемых не отражается на сходимости-расходимости ряда. Обозначим сумму (2), если он сходится через 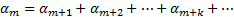 тогда S=S_m+α_m

Теорема 2.

Если (1) сходится, то сумма 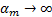 (его остатка);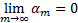

Теорема 3.

a₁+a₂+…+a_n+…=S – сходится, то С*a₁+…+C*a_n+…=C*S C – const тоже сходится.

Теорема 4.

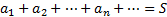
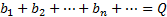тогда:

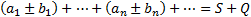
Теорема 5. (необходимое условие сходимости)

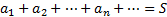 (*) сходится

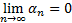
Доказательство:

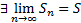
Тогда 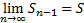, так как при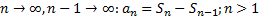

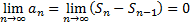
Следствие (достаточное условие расходимости)

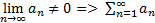 (ряд расходится)

 

Критерий сходимости положительных рядов.

Положительный – ряд, все члены которого неотрицательны.

Пусть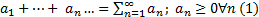

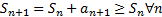
{S_n} – неубывающая последовательность чисел.

Поэтому вопрос о сходимости положительного ряда равносилен вопрос о наличии предела у неубывающей последовательности чисел. Расходимость может означать лишь то, что

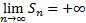
Для того, чтобы положительный ряд (1) сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.

 

Гармонический ряд.

Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных числам натурального ряда:

т.е. сумма всех чисел вида 1/n, где n - натуральное число, изменяющееся от единицы до бесконечности.

Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних.

Гармонический ряд это 1+1\2+1\3+1\4...и так далее где 1, 2, 3, 4, ... - натуральные числа, они стоят по порядку в знаменателе гармонического ряда.

 

Признаки сравнения.

Признаки сравнения применяются для исследования числовых рядов, члены которых неотрицательны, т.е. больше или равны нулю. Такие ряды называются знакоположительными.

Первый признак сравнения:

Пусть заданы два положительных ряда 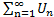 и .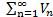

Если начиная с некоторого номера n0 выполнено неравенств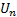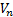о ≤ , то:

если ряд 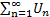 расходится, то ряд  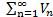будет расходящимся.

если ряд 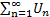 сходится, то ряд  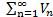будет сходящимся.

Т.е. если ряд с меньшими членами не имеет суммы (расходится), то и ряд с большими членами тоже будет расходиться и если ряд с большими членами имеет сумму (сходится), то и ряд с меньшими членами тоже будет сходиться.

Второй признак сравнения:

Пусть заданы два положительных ряда 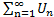 и .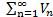

Если при условии 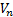≠0 существует предел

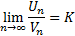
где 0<K<∞, то ряды 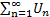 и 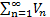сходятся либо расходятся одновременно.

Для применения признаков сравнения нам нужно иметь некий ряд, сходимость которого известна заранее. Чаще всего в роли ряда для сравнения выступает обобщённый гармонический ряд

 (*)

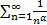Если α>1, то ряд (*) сходится, а если α≤1, то ряд (*)расходится.

Особо стоит обратить внимание на случай α=1, т.е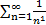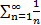. ряд = . Ряд 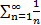 называют гармоническим рядом. Гармонический ряд расходится.

 

 

Признак Даламбера.

Пусть 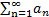− ряд с положительными членами. Тогда справедливы следующие свойства:

• Если 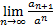<1, то ряд 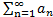сходится;
• Если 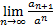>1, то ряд 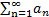расходится;
• Если 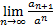=1, то ряд 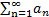может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.

Признак Коши.

Пусть дан ряд (А). а_n≥0 Ɐn, если существует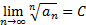

C<1 – (А) сходится

C>1 – (А) расходится

C=1 – признак не работает