ДУ с разделяющимися переменными.
Уравнения вида: М(х)*Р(у)dx+N(x)*Q(y)dy=0 (1) (M(x),N(x),P(y),Q(y) — известные непрерывные функции) называются ДУ с разделяющимися переменными.
Названия уравнения объясняется тем, что в нем модно отделить друг от друга переменные, уединим в одной части х и dx, в другой — у и dy.
M(x)dx/N(x)=-Q(y)dy/P(y)
∫M(x)dx/N(x)=- ∫Q(y)dy/P(y) (4 — общий интеграл)
Произвольная постоянная С входит в состав неопределенных интегралов.
Замечание: при делении (1) на Р(у)*N(x) могут быть потеряны решения. Поэтому надо решить отдельно: Р(у)*N(x)=0 и установить те решения, которые не могут быть получены избобщего решения (особое решение).
Линейные ДУ первого порядка. Уравнения Бернулли.
Уравнение вида: у’+Р(х)*у=f(x), где Р(х),f(x) — известные непрерывные функции; у,у’ — входят в уравнение 1-й степени и нигде между собой не перемножаются.
y=uv, u=u(x), v=v(x)
Действительно, любую функцию можно обозначить у(х)=у(х)/v(x) (1); v(x)=u(x)*v(x), где v(x)≠0.
y’=u’v+uv’
u’v+uv’+P(x)uv=f(x)
u’v+u(v’+P(x)v)=f(x)
v’+P(x)v=0 и u’v=f(x)
dv/dx=-P(x)v
dv/v=-P(x)dx
ln|v|=- ∫P(x)dx
v=e^( - ∫P(x)dx); v=0
Найдем u(x). Она должна быть такой, чтобы при v(x) произведение было решением (1)
u’*e^( - ∫P(x)dx)=f(x)
du/dx=f(x)*e^(∫P(x)dx)
du=e^(∫P(x)dx)*f(x)dx
u= ∫e^( ∫P(x)dx)*f(x)dx+C
y=uv
Этот способ (способ Бернулли) сводит решение линейного уравнения к решению двух уравнений с разделяющимися переменными.
Замечание: уравнения вида у’+Р(х)у=f(x)y^m, m∈ℝ, m≠0,1 — уравнения Бернулли. Подстановкой у^-m+1=z уравнение Бернулли сводится к линейному, но на практике уравнение (1), не сводя к линейному решают способом y=uv, m=0 ((1) — линейное); m=1 ((1) — с разделяющимися переменными).
Однородные ДУ первого порядка и приводящиеся к ним.
z=f(x,y) – однородная функция порядка m∈ℤ, если ∀k выполняется f(Kx, Ky)=Kmf(x,y).
Определение 1: у’=f(x,y) (1) однородное ДУ 1-го порядка, если f(x,y) – однородное 0-го порядка. Покажем, что (1) можно записать как: у’=φ(х/у) (1’).
Действительно, так как f(x,y) – однородная функция 0-го порядка, следовательно f(Kx,Ky)=f(x,y) (2)
Пусть К=1/х, тогда:
k(x,y)=f(1/x*x,1/y*y)=f(1,y/x)= φ(y/x)
Подстановка у/х=t, следовательно у=xt, следовательно у’=1t+xt’
Преобразуем 1’ в уравнение с разделяющимися переменными:
Из 1’ имеем: t+xt’=φ(t)
xt’=φ(t)-t
xdt/dx=φ(t)-t
xdt=(φ(t)-t)dx
dt/(φ(t)-t)=dx/x
Находим общее решение/интеграл и делаем замену и получаем общее решение/интеграл исходного уравнения.
Определение 2: Р(х,у)dx+Q(x,y)dy=0 (3) — однородное ДУ, если Р(х,у) и Q(x,y) — однородные функции одинакового порядка.
y/x=t, следовательно y=xt, следовательно dy=xdt+tdx
Преобразуем (3) в уравнение с разделяющимися переменными.
Уравнения в полных дифференциалах.
P(x,y)dx+Q(x,y)dy=0 (1)
P(x,y),Q(x,y) — непрерывны, дифференцируемы в области D
Условие: ∂P/∂x=∂Q/∂x (2) (непрерывны в D)
При выполнении равенства (2), в левой части уравнения (1) стоит полный дифференциал некоторой функции u(x,y).
Из (1) получаем: du(x,y)=0, следовательно общее решение/интеграл (1): u(x,y)=C, C=const.
Дифференциальные уравнения второго порядка. Общее и частное решения. Существование и единственность решения задачи Коши.
ДУ второго порядка — уравнение, связывающее независимую переменную, искомую функцию и ее первые две производные.
F(x,y,y’,y”)=0 (1)
y”=f(x,y,y’) (2)
Решением ДУ 2-го порядка называется любая функция у=φ(х,у), которая при подстановке в уравнение обращает его в верное равенство.
Общим решением ДУ 2-го порядка называется функция у=φ(х,С1,С2), содержащая 2 произвольные постоянные и удовлетворяющая условия:
1) у=φ(х,С1,С2) является решением (1) при любых произвольных значениях С1 и С2.
2) Каковы бы ни были у(х=х0)=у0; у’(х=х0)=у0’ существует единственное значение постоянных С1=C 1 и С2=С2, такие, что у=φ(х,С1,С2), являются решением уравнения (1) и удовлетворяет начальным условиям (3).
Всякое решение (1) у=φ(х,С1,С2), получающееся из общего решения при фиксированном значении С1 и С2 называется частным решением (1). Решения (1), полученные в виде Ф(х,у,С1,С2)=0 и Ф(х,у,С1,С2)=0 называются общим и частным интегралом соответственно.
График решения — интегральная кривая.
Теорема Коши: если в некоторой окрестности точки (х0,у0) функция f(x,y) определена, непрерывна и имеет непрерывную частную производную, то существует такая окрестность точки (х0,у0), в которой задача Коши имеет решение и притом единственное.
Доказательство:
Найдем y’=k0*ek0x
y”=k02*ek0x
из (1) => k02ek0x+P*k0*ek0x+Q*ek0x=ek0x(k02+Pk+Q)=0 => y=ek0x — решение (1)
Теорема 2:
Общее решения (1) моджет быть написано по одной из след. Формул:
1) k1≠k2; k1,k2∈ℝ => yoo=C1ek1x+C2ek2x; C1,C2 — const;
2) k1=k2; k1,k2∈ℝ => yoo=C1ek1x+C2xek2x; C1,C2 — const;
3) k1,2=α±βi, α,β∈ℝ y=eαx(C1cosβx+C2sinβx) i2=-1;
Доказательство:
1 случай:
Пусть k1 и k2 — корни (2), k1≠k2, тогда у1=ek1x и у2=ek2x — решение (1) по Т1;
у1/у2=еk1x/ek2x=ek1x-k2x=ex(k1-k2) ≠const, т.к. k1≠k2 => y1 и у2 — линейно независимые => по теореме о структуре решения ЛОДУ: уоо=С1еk1x+C2ek2x, C1,C2 — const.
2 случай:
k1=k2 => по Т1 y1=ek1x – решение (1)
Рассмотрим y2=xek1x, покажем, что оно является решением (1):
y2’=ek1x+xk1ek1x
y2”=k1ek1x+k1ek1x+k12xek1x=+k12ek1x
2k1ek1x+ k12xek1x+P(ek1x+xk1ek1x)+Q(xek1x)=ek1xx(k12+Pk1+Q)+2ek1x(k1+P/2)
y2=xek1x – решение (1)
у1 и у2 – линейно независимые, т.к. у2/у1=xek1x/ek1x=x≠const => y1 и у2 – линейно независимые.
По теореме о структуре решение ЛОДУ: Уоо=С1уk1x+C2xek1x
3 случай:
k1=α±βi, тогда по Т1 e(α±βi)x – решение.
eα+βi=eα(cosβ+isinβ) – формула Эйлера.
e(α±βi)х=eαх(cosβ±isinβ) – решение (1)
у1=eαxcosβx и у2=eαxsinβx – взятые в отдельности - решения (1)
функция у1 и у2 – линейно независимые, т.к. у2/у1=tgβx≠const
у1 и у2 – линейно независимые, тогда по теореме о структуре решения ЛОДу 2-го порядка Уоо=С1eαxcosβx+С2eαxsinβx или Уоо=eαx(С1cosβx+С2sinβx)
Следствие:
Частное решение уравнений (их сумма) у”+Py’+Qy=f1(x) у”+Py’+Qy=f2(x) дают частное решение уравнения у”+Py’+Qy=f1(x)+f2(x)
Системы обыкновенных ДУ.
Системой ДУ называется совокупность, в каждое из которых входит независимая переменная, искомые функции и их производные.
Всегда предполагается, что число уравнений системы равно числу неизвестных функций.
Решением системы ДУ называется совокупность функций, при подстановке которых в каждое уравнение системы получается верное равенство.
Нормальной системой ДУ называется система уравнений вида:
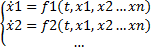 (1)
(1)
Обычно нормальную систему ДУ (1) можно заменить одним ДУ, порядок которого равен числу уравнений системы.
Общее решение (1) имеет вид:

Для нормальных систем ДУ имеет место теорема, гарантирующая существование и единственность частного решения.
Теорема 1.
Если (1) сходится, то сходится и любой из его остатков (2). И обратно, если (2) сходится, то сходится и исходный (1). Другими словами, отбрасывание в начале ряда или приписывание конечного числа слагаемых не отражается на сходимости-расходимости ряда. Обозначим сумму (2), если он сходится через 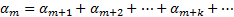 тогда S=Sm+αm
тогда S=Sm+αm
Теорема 2.
Если (1) сходится, то сумма  (его остатка);
(его остатка); 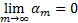
Теорема 3.
a1+a2+…+an+…=S – сходится, то С*a1+…+C*an+…=C*S C – const тоже сходится.
Теорема 4.
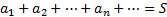
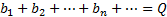 тогда:
тогда:
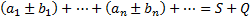
Гармонический ряд.
Гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных числам натурального ряда:
т.е. сумма всех чисел вида 1/n, где n - натуральное число, изменяющееся от единицы до бесконечности.
Ряд назван гармоническим так как каждый его член, начиная со второго, является гармоническим средним двух соседних.
Гармонический ряд это 1+1\2+1\3+1\4...и так далее где 1, 2, 3, 4, ... - натуральные числа, они стоят по порядку в знаменателе гармонического ряда.
Признаки сравнения.
Признаки сравнения применяются для исследования числовых рядов, члены которых неотрицательны, т.е. больше или равны нулю. Такие ряды называются знакоположительными.
Первый признак сравнения:
Пусть заданы два положительных ряда 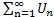 и
и  .
.
Если начиная с некоторого номера n0 выполнено неравенство 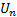 ≤
≤ 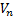 , то:
, то:
если ряд  расходится, то ряд
расходится, то ряд  будет расходящимся.
будет расходящимся.
если ряд  сходится, то ряд
сходится, то ряд  будет сходящимся.
будет сходящимся.
Т.е. если ряд с меньшими членами не имеет суммы (расходится), то и ряд с большими членами тоже будет расходиться и если ряд с большими членами имеет сумму (сходится), то и ряд с меньшими членами тоже будет сходиться.
Второй признак сравнения:
Пусть заданы два положительных ряда 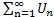 и
и  .
.
Если при условии 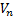 ≠0 существует предел
≠0 существует предел

где 0<K<∞, то ряды  и
и 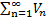 сходятся либо расходятся одновременно.
сходятся либо расходятся одновременно.
Для применения признаков сравнения нам нужно иметь некий ряд, сходимость которого известна заранее. Чаще всего в роли ряда для сравнения выступает обобщённый гармонический ряд
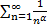 (*)
(*)
Если α>1, то ряд (*) сходится, а если α≤1, то ряд (*)расходится.
Особо стоит обратить внимание на случай α=1, т.е. ряд  =
= 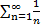 . Ряд
. Ряд 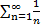 называют гармоническим рядом. Гармонический ряд расходится.
называют гармоническим рядом. Гармонический ряд расходится.
Признак Даламбера.
Пусть 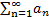 − ряд с положительными членами. Тогда справедливы следующие свойства:
− ряд с положительными членами. Тогда справедливы следующие свойства:
- Если
 <1, то ряд
<1, то ряд 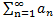 сходится;
сходится; - Если
 >1, то ряд
>1, то ряд 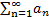 расходится;
расходится; - Если
 =1, то ряд
=1, то ряд 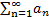 может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.
может как сходиться, так и расходиться. В этом случае для установления сходимости нужно использовать другие признаки.
Признак Коши.
Пусть дан ряд (А). аn≥0 Ɐn, если существует 
C<1 – (А) сходится
C>1 – (А) расходится
C=1 – признак не работает
Теорема Лейбница
Если члены знакочередующегося ряда (1) по абсолютной величине монотонно убывают
1) a1>a2>…>an>…n
2) стремится к 0 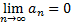 , то знакочередующийся ряд (1) сходится и его сумма 0<S<a1
, то знакочередующийся ряд (1) сходится и его сумма 0<S<a1
Следствие
Остаток rn ряда лейбницкого типа имеет знак своего первого члена и меньше его по абсолютной величине.
Теорема
Ряд (*) всегда сходится и имеет ту же самую сумму, что и данный ряд (А), т.е. сходящиеся ряды обладают сочетательными свойством.
Замечание
Эта аналогия с конечными суммами нарушается, если применить сочетательное свойство в "обратном порядке". Если (*) сходится, члены которого представляют собой суммы конечного числа членов ряда А, то опустив скобки получим ряд, который может оказаться расходящимся.
Например:
(1-1)+(1-1)+…+(1-1)+… - сходится
1-1+1-1+1-1+…+1-1+… - расходится
Теорема Дирихле
Абсолютно сходящиеся ряды обладают переместительными свойствами
Теорема Римана
Если ряд сходится условно, то путём перестановки его членов, можно получить ряд, имеющий наперёд заданную сумму, а также расходящийся ряд, т.е. условно сходящиеся ряды переместительным свойством не обладают.
Замечание
Различия между абсолютно и условно сходящимися рядами заключается в том. что условная сходимость осуществляется благодаря взаимному погашению положительных и отрицательных членов ряда и поэтому существенно зависит от того, в каком порядке члены ряда следуют друг за другом. А абсолютная сходимость основана на быстроте убывания этих членов и не зависит от порядка их следования друг за другом.
Теорема Абеля
Если ряд (1) сходится при некотором значении х0, отличном от 0, то он сходится и при абсолютном и для всех значений х: IxI<Ix0I
Если ряд (1) расходится при некотором значении х0, то он расходится для всех х: IxI>Ix1I
Для ряда (1) логически могут представляться 3 возможности
1. Ряд (1) сходится только в х=0
2. Ряд (1) сходится на всей числовой прямой
3. Ряд (1) сходится не только в точке х=0, но и не на всей числовой прямой
Теорема
Ряд (1) сходится не только в точке х=0, но и не на всей числовой прямой, то существует R>0, такое, что для любых IxI<R ряд (1) сходится абсолютно, а для всех IxI>R ряд (1) расходится.
Число R - радиус сходимости степенного ряда (-R; R) - интервал сходимости.
Если ряд (1) сходится только в ч=0, то полагают R=0. Если ряд (1) сходится на всей числовой прямой, то R= 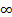 . Поведение ряда в точках x=
. Поведение ряда в точках x= 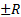 может быть разным. Надо отдельно исследовать поведение x=R и x=-R.
может быть разным. Надо отдельно исследовать поведение x=R и x=-R.
Исследовать степенной ряд на сходимость значит: найти его интервал сходимости и выяснить, как ведёт себя ряд в граничных точках интервала сходимости.
Область сходимости степенного ряда всегда состоит из интервала сходимости и может быть из граничных точек интервала сходимости.
Для нахождения радиуса сходимости степенного ряда есть формула
R= 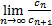 (*)
(*)
или
R=  (**)
(**)
Но формулам (*) и (**) пользоваться нельзя, если в ряде (1) отсутствуют какие-то степени х (Ряд содержит только чётные или нечётные степени х). В этом случае пользуются признаком Даламбера для абсолютной сходимости. Этот способ можно применять всегда.
Свойства степенных рядов.
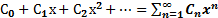 (1)
(1)
Теорема 1:
Сумма степенного ряда (1) есть функция, непрерывная в каждой точке интервала сходимости.
Теорема 2:
Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости.
Теорема 3:
Степенной ряд можно почленно интегрировать по любому промежутку, лежащему в интервале сходимости.
Замечание (2 и 3):
R рядов (2) и (3) такие же как и у исходного (1). 1+2х+3х2… получен из дифференцирования 1+х+х2… геометрическая прогрессия с b1=1 b q=x => -R<a<x<R
Доказательство:
f’(x)=C1+2C2(x-x0)+3C3(x-x0)2+…+nCn(x-x0)n-1…R
f’’(x)=1*2C2+2*3C3(x-x0)+…+n(n-1)Cn(x-x0)n…R
Коэффициент ряда 2 определяется однозначно Cn=fn(x0)/n! (v)
Подставим полученное выражение в (2)
f(x)=f(x0)+f’(x0)/1!*(x-x0)+f’’(x0)/2!*(x-x0)+…(vv) – ряд Тейлора.
Замечание:
Если в (vv) х0=0, то получим частный случай ряда Тейлора: f(x)=f(0)=fn(0)*xn/n!+… - ряд Маклорена.
Ряды Тейлора и Маклорена.
Теорема:
Если f(x) на (x0-R; x0+R) разлагается в f(x)=С0+С1(х-х0)+С2(х-х0)2+…+Сn(х-х0)n+…(2), то это разложение единственно.
Доказательство:
f’(x)=C1+2C2(x-x0)+3C3(x-x0)2+…+nCn(x-x0)n-1…R
f’’(x)=1*2C2+2*3C3(x-x0)+…+n(n-1)Cn(x-x0)n…R
Коэффициент ряда 2 определяется однозначно Cn=fn(x0)/n! (v)
Подставим полученное выражение в (2)
f(x)=f(x0)+f’(x0)/1!*(x-x0)+f’’(x0)/2!*(x-x0)+…(vv) – ряд Тейлора.
Замечание:
Если в (vv) х0=0, то получим частный случай ряда Тейлора: f(x)=f(0)=fn(0)*xn/n!+… - ряд Маклорена.
Ряд Тейлора можно составить для любой функции, бесконечно дифференцируемой в окрестности х0.
f(x0)+…+fn(х0)/n!*(x-x0)n+… (vvv)
Ряд (vvv) как и всякий степенной ряд по степеням х сходится в точке х=0. Но возникает вопрос, сходится ли этот ряд где-нибудь еще и если сходится, то что является суммой ряда. Функция f(x) с помощью которой вычисляют коэффициенты или какая-нибудь другая функция.
В дифференциальном исчислении установлена формула Тейлора:
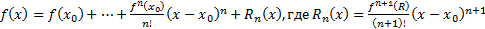 , где С между х и х0, Rn(x) – остаточный член в формуле Тейлора в форме Лагранжа.
, где С между х и х0, Rn(x) – остаточный член в формуле Тейлора в форме Лагранжа.
Теорема 1:
Для того, чтобы ряд Тейлора функции f(x) в промежутке (x0-R; x0+R) сходился и имел своей суммой функцию f(x), необходимо и достаточно, чтобы остаточный член Rn(x) в формуле Тейлора стремился к нулю при 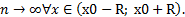
Выражение для Rn(x)-го бывает очень громоздким и поэтому трудно установить стремится Rn(x) к нулю или нет.
Теорема 2 (достаточное условие сходимости ряда Тейлора функции f( x) к функции f( x)):
Если в (x0-R; x0+R) функция f(x) имеет производные любого порядка и все они ограничены по абсолютной величине одним и тем же числом, то ряд Тейлора функции f(x) в (x0-R; x0+R) сходится к функции f(x).
Теорема Дирихле:
y=f(x) T=2π [-π; π] удовлетворяет условия:
1) f(x) непрерывна на [-π; π] или имеет на этом отрезе конечное число точек разрыва 1-го рода;
2) f(x) монотонна на [-π; π] или [-π; π] можно разбить на конечное число частей, на каждой из которых f(x) изменяется монотонною
3) Сумма в граничных точках равна 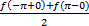
ДУ с разделяющимися переменными.
Уравнения вида: М(х)*Р(у)dx+N(x)*Q(y)dy=0 (1) (M(x),N(x),P(y),Q(y) — известные непрерывные функции) называются ДУ с разделяющимися переменными.
Названия уравнения объясняется тем, что в нем модно отделить друг от друга переменные, уединим в одной части х и dx, в другой — у и dy.
M(x)dx/N(x)=-Q(y)dy/P(y)
∫M(x)dx/N(x)=- ∫Q(y)dy/P(y) (4 — общий интеграл)
Произвольная постоянная С входит в состав неопределенных интегралов.
Замечание: при делении (1) на Р(у)*N(x) могут быть потеряны решения. Поэтому надо решить отдельно: Р(у)*N(x)=0 и установить те решения, которые не могут быть получены избобщего решения (особое решение).
Дата: 2019-02-19, просмотров: 299.