Момент импульса материальной точки - векторное произведение радиуса-вектора материальной точки на ее импульс
L=[r p]
Момент импульса твердого тела - сумма моментов импульса отдельных частиц или произведение момента инерции тела относительно той же оси на угловую скорость:
L=I⋅ω, где ω - угловая скорость, I - момент инерции твердого тела
Абсолютно твердое тело. Основной закон динамики вращательного движения твердого тела относительно неподвижной оси.
Абсолютно твёрдое тело - тело, которое ни при каких условиях не может деформироваться и всегда расстояние между двумя точками (частицами) этого тела остаётся постоянным.
Основной закон динамики вращательного движения твёрдого тела относительно неподвижной оси:
Угловое ускорение, приобретаемое телом, вращающегося относительно неподвижной оси, пропорционально моменту всех внешних сил, действующих на тело и обратно пропорционально моменту инерции I относительно оси.
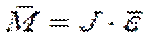 , ε - угловое ускорение, J - момент инерции, M - момент всех внешних сил
, ε - угловое ускорение, J - момент инерции, M - момент всех внешних сил
Закон сохранения момента импульса.
В замкнутой системе момент импульса твердого тела относительно любой неподвижной точки не изменяется с течением времени как по величине, так и по направлению.
M=dL/dt => dL=0 => L=const
Гармонические колебания. Уравнение гармонических колебаний.
Гармонические - колебания, при которых физическая величина изменяется с течением времени по гармоническому закону.
x=x m cos(ωt + φ 0 )
x – смещение тела от положения равновесия
xm – амплитуда колебаний - максимальное смещение от положения равновесия
ω – циклическая или круговая частота колебаний - число колебаний за 2π секунд
t – время
φ0 – начальная фаза - начальное положение
φ =ωt+φ0 - фаза гармонического процесса
Период колебаний T - минимальный интервал времени, через который происходит повторение движения тела
Частота колебаний f (герц, Гц) показывает, сколько колебаний совершается за 1 с
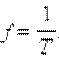
Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:
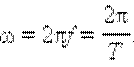
Фаза - аргумент периодической функции, описывающей колебательный или волновой процесс.
Гармонические колебания. Дифференциальные уравнения гармонических колебаний.
Уравнение дает зависимость колеблющейся величины S от времени t; это и есть уравнение свободных гармонических колебаний в явном виде. Однако обычно под уравнением колебаний понимают иную запись этого уравнения, в дифференциальной форме. Возьмем для определенности уравнение в виде 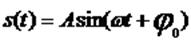
Дважды продифференцируем его по времени:
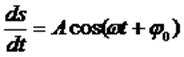
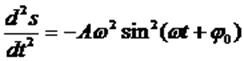
Видно, что выполняется следующее соотношение:
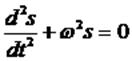
Дата: 2019-02-19, просмотров: 309.