В зависимости от степени сложности изучаемого явления и от поставленных задач статистические группировки могут выполняться по одному или нескольким группировочным признакам. Группировка называется простой (одномерной), если однородные группы формируются по одному признаку. Если однородные группы образуются по двум и более признакам, то группировка называется сложной. В классе одномерных группировок выделяют следующие типы:

- структурные – предназначены для выявления состава изучаемого явления;

- типологические – предназначены для выделения в статистической совокупности различных социально-экономических типов явлений;

- аналитические (факторные) – используются для изучения связей и зависимости между варьирующими признаками.

Чтобы построить группировки, необходимо выполнить некоторые требования:

— группировки должны охватывать все, без исключения существенные стороны явления;

— система должна включать все виды группировок по решаемым задачам;

— группировки не должны противоречить друг другу.

— группировки по качественным признакам должны предшествовать группировкам по количественным признакам;

— таблицы в системе группировок должны иметь стабильную нумерацию;

— результативные признаки в группировках должны быть со­поставимы, то есть измерены в одинаковых единицах;

— интервалы группировок должны быть неизменными из года в год.

Рассмотрим структурные группировки. Структурные группировки используются для изучения внутреннего строения статистической совокупности и характеристики структурных сдвигов.

Они дают информацию о текущем состоянии массовых явлений и применяются в целях оперативного управления. Структурная группировка выполняется в несколько этапов:

- выбор группировочного признака;

- определение необходимого числа групп;

- определение параметров групп;

- распределение единиц наблюдения по выделенным группам;

- расчет структурных характеристик;

- формулировка выводов.

Выбор группировочного признака осуществляется в соответствии с целями статистического исследования. В качестве группировочного обычно выступает существенный признак. Обязательным условием выполнения любой группировки, в том числе и структурной являетсяупорядочение статистической совокупности по значениям группировочного признака.

Определение необходимого числа групп. Число групп должно быть достаточным для объективного представления изучаемой совокупности. При большом числе групп различия между ними становятся малозаметными, а в самих группах в виду их малой наполняемости перестает действовать закон больших чисел и возможно проявления случайности. При малом же их числе в одну группу могут попасть статистические единицы с существенно различающимися значениями признака. На количество выделяемых групп влияют следующие факторы:

- уровень колеблемости группировочного признака - чем значительнее вариация признака, тем большее количество групп необходимо выделять при прочих равных условиях;

- размер изучаемой статистической совокупности - чем больше размер исследуемой совокупности, тем большее количество групп необходимо выделять.

Выделенные группы должны быть достаточно заполненными. Наличие незаполненных групп или малое число статистических единиц в них свидетельствуют о неправильном определении их числа.

Ориентировочно число групп можно определить используя эмпирическую зависимость, называемую «формулой Стерджесса»:

n=1+3.322*lg*N                                                    (1)

где: n– количество групп

N - численность единиц статистической совокупности

Существует еще один способ определения количества выделяемых групп, он связан с применением среднеквадратичного отклонения: если ширина интервала равна 0,5a, то выделяется 12 групп, если 2/3a, то 9 групп, если a, то 6 групп.

Определение параметров группы. В каждой выделенной группе рассчитываются следующие параметры:

- верхняя граница интервала ;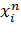

- нижняя граница интервала ;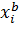

 ширина интервала ;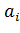

 середина интервала .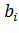

Нижней границей интервала 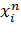 называется наименьшее значение признака в группе. Верхней    границей в интервала 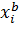называется наибольшее значение признака в группе. Интервалы группировки бывают равными и неравными (прогрессивно возрастающими, прогрессивно убывающими, произвольными, специализированными). Если вариация признака проявляется в сравнительно узких границах, и распределение статистических единиц носит достаточно равномерный характер, то строят группировку с равными интервалами. Для равно интервальной группировки ширина интервала 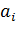определяется по формуле:

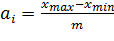=                                                                       (2)

где R – размах вариации,R =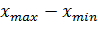

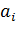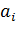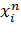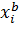При определении размаха вариации R из наблюдения исключаются аномальные значения признака. Полученное значение ширины интервала округляется в бóльшую сторону. На основе рассчитанной ширины интервала последовательно определяется границы интервалов  и  . Определение границ начинаетсяс первой группы. Ее нижняя граница должна быть не более минимального значения признака в совокупности, т.е. 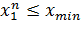, верхняя граница определяется как .                                          

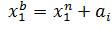Для второй группы нижняя граница принимается равной верхней границе первой группы, т. е. 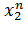= 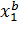, верхняя определяется как  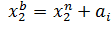и т.д. В целом границы интервалов определяются формулами:

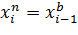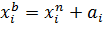;                                                   (3)

Середина интервала (центральная варианта) 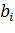определяется как полусумма    верхней и нижней границ, т.е. по формуле:  

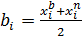.                                                                                         (4)

Параметр середина интервала используется при расчете обобщающих характеристик изучаемой совокупности. Достаточно часто при выполнении группировки используются открытые интервалы. В открытых интервалах указывается только одна граница: верхняя - у последнего интервала, нижняя – у первого. Для закрытия таких интервалов необходимо предварительно определить их ширину. Проблема ширины открытых интервалов решается следующим образом: при равноинтервальной группировке она есть величина постоянная; при неравноинтервальной - предварительно определяется закономерность изменения ширины интервала для некрайних групп - выявленная закономерность позволяет определить ширину соответствующего интервала и рассчитать недостающую границу.

Распределение единиц совокупности по группам. Основной задачей данного этапа является подсчет числа единиц, попавших в каждую из выделенных групп - 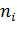. При распределении единиц наблюдения по выделенным группам, особенно если группировочный признак является непрерывным, имеет место неопределенность: к какой группе относить единицы со значениями признака, совпадающими с границами интервалов? Для устранения неопределенности используют принцип единообразия – такие единицы включаются в группу, в которой нижняя граница совпадает со значением признака.

Расчет структурных характеристик. Расчет заключается в определении для каждой группы удельного веса (доли) ее единиц в общем объеме статистической совокупности.  Как и любая относительная величина, этот показатель может быть определен в виде коэффициентов:

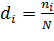;                                                                   (5)

или в виде процентов:

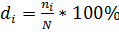                                                                (6)

Рассчитав такие доли для всех групп, мы получаем структуру изучаемой статистической совокупности, равную полному набору долей:

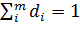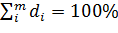или                                                    (7)

Формулировка выводов о составе совокупности. Выводы делаются на основе анализа показателей структуры, в них отражаются два положения:

1. Какие значения признака встречаются в совокупности наиболее часто, какие наиболее редко.

2. Каков характер изменения структуры в зависимости от изменения значения признака. С увеличением значения признака доля может увеличиваться, либо уменьшаться. Это довольно типично для экономических показателей.

Выводы должны быть сделаны обязательно, иначе пропадает смысл группировки.