Задание № 7 (с. 25).
– Что изображено на чертеже?
– Что называют числовым лучом?
– Чему равен единичный отрезок?
– Что называют координатой точки?
– Определите, какая точка имеет координату 5, 9, 11? (А(5); Е(9); К(11).)
Задание № 8 (с. 25).
Перед выполнением задания учитель просит учащихся внимательно рассмотреть числовой луч. На рисунке изображена та его «часть», на которую не попало начало луча, и, кроме того, не указан единичный отрезок. Чтобы выполнить задание, надо прежде всего выяснить, каков единичный отрезок. Ясно, что между точками (30) и В(31) ровно 1 единичный отрезок. Видно, что между точками А(25) и В(31) 6 таких единичных отрезков, поэтому координаты точек, отмеченных на луче между этими точками, соответственно, 26, 27, 28, 29 и 30.

Задание № 9 (с. 25).
Сложность задания в том, что выполнять его надо без опоры на наглядность, то есть у учащихся не должен быть перед глазами числовой луч с отмеченными на нем точками А, В, С, М и Е. Пользоваться надо правилом сравнения чисел с помощью числового луча.
– Сравните координаты точек, отмеченных Юрой на числовом луче.
– Какая из координат является наименьшей?
– Как расположена на числовом луче точка с этой координатой по отношению к остальным точкам?
– Какая из координат является наибольшей?
– Назовите слева направо все отмеченные на числовом луче точки.
– Какая из точек ближе всех к точке В?

V. Повторение пройденного материала.
1. Работа в печатной тетради № 1.
Задание № 35.
Задание состоит из двух частей. Сначала надо попросить учащихся внимательно рассмотреть все три числовых луча и выбрать тот, на котором можно отметить точки с заданными координатами. Дети должны понимать, что теоретически на любом числовом луче можно отметить точки с любыми координатами, но практически это можно выполнить, лишь изобразив подходящую часть луча. С этой точки зрения среди представленных числовых лучей, безусловно, единственно удобным является нижний луч. Далее можно переходить к выполнению второй части задания. Предложите детям самостоятельно отметить точки с координатами 38, 40 и 44.
Задание № 36.
Между точками с координатами 60 и 61 один единичный отрезок. Если мы будем двигаться влево от точки (60) и последовательно откладывать единичные отрезки, то координаты отмеченных там точек будут таковы: 59, 58 и 57. Двигаясь вправо от точки (61) и также последовательно откладывая единичные отрезки, мы получим такие координаты оставшихся отмеченных точек:

– Что надо определить, прежде чем выполнить построения? (Надо определить единичный отрезок.)
– Сравните единичные отрезки данных числовых лучей.
Задание № 37.
Учащиеся работают самостоятельно.
2. Работа по учебнику.
Задание № 21 (с. 28).
– Прочитайте задачу.
– Что известно в задаче?
– Прочитайте, что требуется найти.
– Все ли числа, необходимые для решения задачи, есть в условии?
– Каким действием можно вычислить возраст кошки Мурки?
– Какие преобразования необходимо выполнить? (1 год = 12 месяцев.)
Решение: 12 – 5 = 7 (м.) – кошке Мурке.
– Изменится ли ответ задачи, если вместо числа 5 в условии будет число 2? (12 – 2 = 10 (м.).)
– Можно ли будет решить задачу, если в условии число 5 заменить числом 14? (Нельзя, так как 12 < 14.)
– Как изменится решение задачи, если слово «моложе» заменить словом «старше»? (Необходимо выполнить сложение.)
Задание № 22 (с. 28).
Учащиеся работают с фишками.
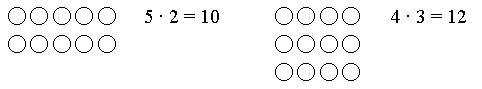
Задание № 23 (с. 29).
Учащиеся записывают выражение к задаче и находят его значение, используя фишки.
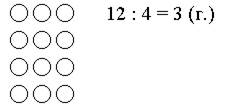
Задание № 26 (с. 29).
– Прочитайте задание.
– Что известно про число? (Число меньше 20, значит, в нем будет 1 десяток. А так как единиц на 6 больше, чем десятков, следовательно, 1 + 6 = 7 (ед.). Задуманное число – 17.)
VI. Итог урока.
– Что нового узнали на уроке?
– Как сравнить числа, используя числовой луч?
Домашнее задание: № 24, 25 (учебник).
Урок 13
Метр. Соотношения между единицами длины
Цели урока : рассмотреть измерения длин и расстояний с помощью измерительных инструментов: линейки, метровой линейки, рулетки; учить сравнивать величины, выраженные в единицах длины; совершенствовать умения решать задачи; развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Отгадайте, имя какого сказочного героя здесь зашифровано.
| 11 + 8 | Й | 11 – 7 | И | |
| 12 – 9 | Л | 13 – 8 | Ч | |
| 14 – 6 | О | 15 – 8 | А | |
| 13 + 5 | Б | 9 + 5 | Т |
| 7 | 19 | 18 | 8 | 3 | 4 | 14 |
| А | Й | Б | О | Л | И | Т |
2. Анализ задач.
Какую из этих задач вы можете решить, а какую – нет? Почему?
а) Таня полила шесть грядок огурцов.
Сколько грядок ей осталось полить?
б) На шахматной доске 20 фигур. Из них 13 черных, остальные – белые. Сколько белых фигур на шахматной доске?
3. Сколькими способами можно прочитать слово «маршрут»?
| м | р | р | т | |||
| а | ш | у | ||||
| м | р | р | т | |||
| а | ш | у |
4. Маша, Оля и Настя заняли призовые места в соревнованиях на коньках. Маша не заняла ни первое, ни второе место. Оля не пришла первой. Какое место заняла каждая из девочек?
III. Сообщение темы урока.
– Мы с вами умеем измерять длины небольших предметов с помощью обычной линейки, получая результаты в сантиметрах. А как быть, если нам надо пойти в магазин и купить отрез ткани на пальто? Неужели продавец будет отмерять ткань такой линеечкой, как наша? Ни один продавец такой линейкой не пользуется, так как в сантиметрах длину большого куска ткани отмерять очень неудобно. Продавцы всегда используют деревянную линейку, которая называется портновским метром.
– Сегодня на уроке мы познакомимся с крупной единицей измерения – метром.
Дата: 2018-12-28, просмотров: 677.