Степень возрастания вариограммы с расстоянием показывает, как быстро уменьшается влияние пробы. После того как вариограмма достигает ее ограничивающего значения (ее порога), корреляции между пробами больше нет. Это критическое расстояние, называется зоной влияния. Для стационарных переменных g(h) эквивалентно дисперсии на расстоянии больше зоны влияния. Это означает, что:
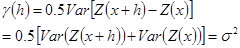 [3.3]
[3.3]
Не все вариограммы достигают порога. Некоторые вариограммы (см. рис. 3.2.) продолжают возрастать с увеличением расстояния. Это свойство является одним из фундаментальных отличий вариограммы от ковариационной функции. Последняя существует только для стационарных переменных и ограничена.
Зона влияния необязательно одинакова во всех направлениях. Поэтому она отражает феномен анизотропии. К тому же, даже для одних и тех же направлений может быть более одной зоны влияния. Это случается когда существует несколько вложенных структур, действующих в разных направлениях по-разному. Примеры анизотропии и вложенных структур будут представлены позже.

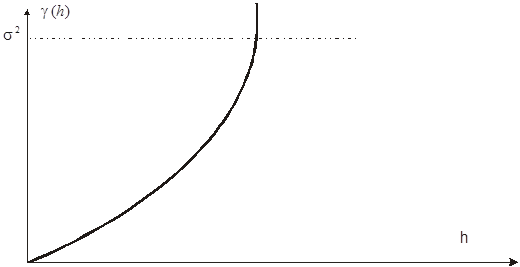
Рис 3.2. Без пороговая вариограмма
Поведение около начала
Мы исследовали поведение вариограммы только на сравнительно больших расстояниях. Но более важно изучить ее поведение для малых значений h, потому что это связано с непрерывностью и пространственной регулярностью исследуемой переменной. На рис. 3.3. изображены четыре типа поведения вариограммы около начала.
1. Квадратичный. Этот тип показывает, что пространственная переменная имеет высокую непрерывность. Фактически это говорит о диференцируемости. Квадратичная форма может также ассоциироваться с присутствием тренда.
2. Линейный. пространственная переменная непрерывна, но не дифференцируема, и, таким образом, менее регулярна, чем предыдущая.
3. С разрывом в начале т.е. g(h) не стремится к нулю, при h близких к 0. Это означает, что переменная в высокой степени нерегулярна на малых расстояниях.
4. Плоский. Чисто случайная функция или «белый шум». Пространственные переменные Z(x+h) и Z(x) некоррелированны для всех значений h, и расстояние между ними не имеет значения. Это предельный случай полного отсутствия структуры. Это, кстати, модель, используемая в анализе поверхности тренда.
Вариограммы большинства геологических переменных, включая содержания металлов, как правило имеют разрыв в начале. Это явление называется эффектом самородка, потому что было впервые отмечено на золотом месторождении в Южной Африке, где его связывали с присутствием в руде самородков золота. Содержание резко изменяется от нуля (снаружи самородка) до высокого значения внутри него. Золото это не единственный минерал, который содержит самородки. Крупицы пирита, случайно расположенные в угле, приводят к неустойчивому изменению в содержании серы. Термин “эффект самородка” также применяется для характеристики непостоянства исследуемой переменной на малых расстояниях даже в том случае, когда известно, что на высокую изменчивость влияет другой фактор, такой как микроструктура руды, ошибка измерения переменной или ошибки в определении местоположения пробы.
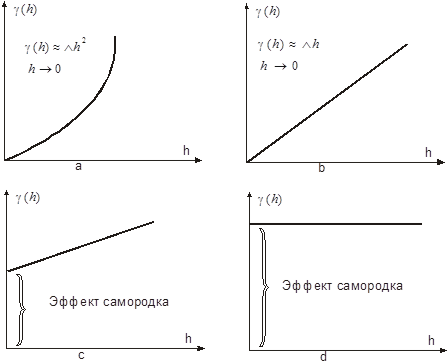
Рис 3.3. Поведение вариограммы около начала. Квадратичная форма (a) показывает высокую степень непрерывности переменной; линейное поведение (b) демонстрирует умеренную непрерывность. Разрыв в начале (c, d) показывает неустойчивое поведение на малых расстояниях, которое называется эффектом самородка.
Анизотропия
Когда вариограмма вычисляется в различных направлениях, то иногда поведение ее бывает различным для некоторых из этих направлений (т.е. наблюдается анизотропия). Если этого не происходит, то вариограмма зависит только от величины расстояния между двумя точками и называется изотропной. Можно выделить два различных типа анизотропии: геометрическую анизотропию и зональную анизотропию.
Геометрическая анизотропия
На рисунке 3.4. изображены примеры геометрической анизотропии. На левом рисунке вариограммы имеют одинаковый порог в обеих направлениях, но зоны влияния различны, в то время, как на правом рисунке обе функции линейны, но имеют разные углы наклона.
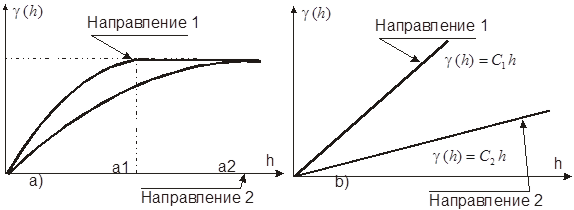
Рис 3.4. Эллиптическая или геометрическая анизотропия
Мы можем нарисовать диаграмму, показывающую зависимость зоны влияния или угла наклона в зависимости от направления. (Рис. 3.5.). Если кривая является эллипсом (в 2-х мерном пространстве), то анизотропия называется геометрической (или эллиптической). В этих случаях простейшими изменениями координат эллипс преобразуется в окружность, и анизотропия устраняется.
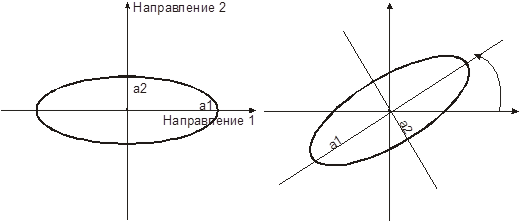
Рис 3.5. Эллипсы, показывающие главные оси эллипса в случае геометрической анизотропии
Это преобразование особенно просто, когда главная ось эллипса совпадает с координатными осями, как показано на Рис. 3.5. (a). Затем если уравнение вариограммы в направлении 1 есть 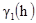 , то общая вариограмма после исправления анизотропии имеет следующий вид:
, то общая вариограмма после исправления анизотропии имеет следующий вид:
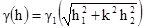 [3.4]
[3.4]
где h1 и h2 – два компонента h, и k – отношение анизотропии, определенное, как:
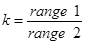 или
или 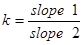 (range – зона влияния , slope – угол наклона ) [3.5]
(range – зона влияния , slope – угол наклона ) [3.5]
При первом вычислении вариограммы, важно исследовать по крайней мере четыре направления. Если вариограмма вычисляется только в двух перпендикулярных направлениях, то анизотропию возможно потерять полностью. Это случается, например, когда главные оси эллипса анизотропии повернуты относительно направлений, в которых рассчитываются вариограммы, на 45 градусов, как показано на Рис. 3.5.b.
Дата: 2018-12-28, просмотров: 495.