Существуют более сложные виды анизотропии. Например, вертикальное направление в слоистом массиве часто играет особую роль, потому что между слоями существует больше различий, чем вдоль них. В этих случаях пороги вариограммы не одинаковы для разных направлений. Существует обычная практика разделять вариограмму на две компоненты, изотропная компонента плюс еще одна, которая действует только в вертикальном направлении:

Изотропная компонента                                     Вертикальная компонента:

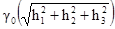
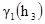                                                          [3.6]

Полная вариограмма g(h) –

                                                                        [3.7]

Присутствие тренда

Как упоминалось в конце Главы 2, теория показывает, что для внутренних и стационарных переменных, вариограмма возрастает медленнее, чем квадрат для больших расстояний. Для большей определенности, можно записать:

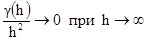                                                                                          [3.8]

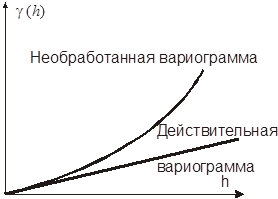
Рис 3.6. Вид вариограммы, свидетельствующий о наличии тренда

Однако, на практике часто случается, что вариограммы возрастают быстрее, чем h². Это указывает на наличие тренда (Рис. 3.6.). Экспериментальная вариограмма обеспечивает оценку 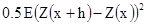, которая называется необработанной вариограммой, в отличие от верной (или основной) вариограммы. Эти две вариограммы совпадают, только если приращение имеет нулевое среднее. Иначе говоря:                                               

E[Z(x+h)-Z(x)]²                   = Var[Z(x+h)-Z(x)]          + (E[Z(x+h)-Z(x)])²              [3.9]

необработанная вариограмма = основная вариограмма + (параметр смещения)²

Если присутствует тренд, то эмпирическая вариограмма переоценивает основную вариограмму.

Вложенные структуры

Глядя на экспериментальные вариограммы, иногда можно увидеть вложенные структуры. На Рис. 3.7. более длинная зона влияния очевидно является вложенной структурой, потому что вариограмма достигает порога на этом расстоянии. Более короткую зону влияния можно распознать по характерному изменению кривизны функции. Это хорошо заметно, когда две зоны влияния достаточно различны. Если нет, то изменение кривизны линии часто не является очевидным.

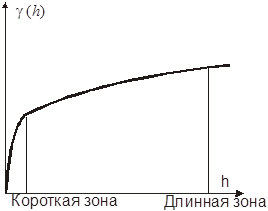
Рис 3.7. Вложенная структура, составленная из структур с короткой и длинной зонами влияния.

Вложенные структуры указывают на присутствие процессов, оперирующих в различных масштабах. Например, это может быть ошибкой измерения на уровне пробы, т.е. для h=0. На петрографической шкале (т.е. h<1 см) это может быть изменчивость, обусловленная переходом от одного минералогического агрегата к другому. На уровне пласта или минерализованой залежи (т.е. для h<100 м) появляется третий тип изменчивости в точке перехода от руды к пустой породе или от одного типа породы к другому.

Пропорциональный эффект

Считается, что вариограмма имеет пропорциональный эффект, когда ее значение (особенно ее порог) пропорционально квадрату локального среднего содержания. Это часто встречается у логнормально распределенных данных. Вариограммы для различных зон имеют одинаковую форму, но порог в богатых зонах намного больше, чем в бедных. Так же как порог часто оказывается пропорциональным квадрату локального среднего содержания, основная вариограммная модель может быть найдена делением значений каждой локальной вариограммы на квадрат локального среднего содержания и затем усреднение полученных величин в процессе подгонки вариограммной модели.

Скважинный эффект и периодичность

Между началом и бесконечностью поведение вариограммы отражает разные варианты поведения, такие как присутствие вложенных структур, иногда, скважинный эффект или даже периодичность. В некоторых случаях экспериментальная вариограмма поднимается до значения порога, а затем падает вниз. Так как этот “бугор” в вариограмме соответствует провалу в ковариационной функции, то этот эффект называется скважинным эффектом. Иногда эту особенность можно объяснить геологически. Одним из подобных примеров является вариограмма, вычисленная Серрой (Serra) (1968) по сечениям железорудной залежи в провинции Лоран (Lorraine) во Франции. Кристаллы кальцита имеют свойство быть разделенными интервалами примерно пропорциональными их размеру, потому что процесс кристаллизации располагает зародыши кристаллов случайным образом. Обычно большинство периодических структур основаны на скважинном эффекте. Но более общая причина этого эффекта обусловлена естественными флуктуациями вариограммы или статистическими флуктуациями, из-за использования слишком малого количества пар точек в вычислении экспериментальной вариограммы.

       Вариограммы, так же как и ковариационные функции могут иметь периодическое поведение. Хотя для временных рядов это свойство является обычным, его достаточно трудно объяснить с позиций геологии. Складчатые напластования однако могут показать периодичность. Но обычно считают, что периодичность искусственно обусловлена скорее человеческой активностью, чем матерью - природой. Например, значения содержаний, полученных в течение ночной смены может статистически отличаться от дневной смены. Каждый раз важно проверять, что эффект настоящий, а не создан искусственно. Один из природных случаев, когда может встретиться периодичность, это когда руда лежит на склонах хребта или ущелья, как это иногда происходит в осадочных месторождениях золота. Вариограммы, вычисляемые в направлениях, перпендикулярных к хребту или ущелья, могут показать периодичность, но в направлениях вдоль складок – нет. Пример этого представлен в Главе 5.

Модели вариограмм

Для использования вариограммы в процессе оценивания к ней должна быть подобрана математическая модель. Причина этого заключается в том, что функции вариограмм должны удовлетворять определенным условиям. Другая причина связана с тем, что всегда существует риск получить отрицательную дисперсию, которая приведет к неприемлемым результатам.