Простейшей иллюстрацией какого-либо распределения может являться таблица с возможными значениями случайной величины и соответствующими вероятностями. Обозначим шары в урне номерами 0, 1, 2, 3, 4 и будем вытаскивать, и класть шары обратно 100 раз. В результате этого опыта мы случайно можем получить следующую частотную таблицу
| N шаров | Число наблюдений, в которых происходило данное событие (mi) | Частость (mi/n) pi |
| 0 | 16 | 0.16 |
| 1 | 56 | 0.56 |
| 2 | 24 | 0.24 |
| 3 | 3 | 0.03 |
| 4 | 1 | 0.01 |
| n = 100 | ∑ = 1 |
Что бы изобразить это графически по горизонтальной оси откладывают отрезки пропорциональные значениям, а по вертикальной оси откладывают отрезки пропорциональные частостям - pi. Графическое изображение строят или в виде полигональной кривой или гистограммы.
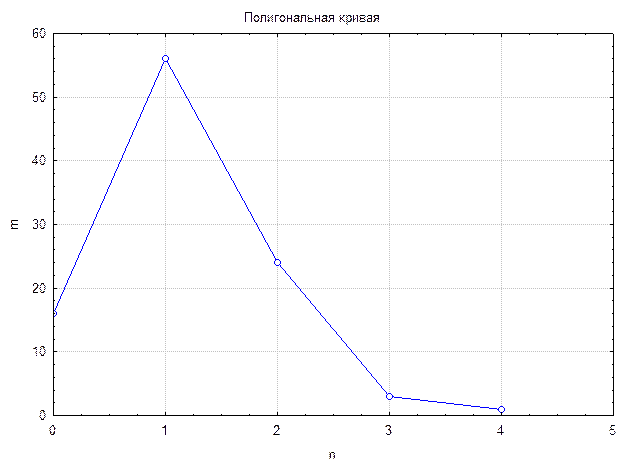 Полигональные кривые используются в большей мере при изображении распределений дискретных величин. Для построения полигональной кривой по оси абсцисс откладывают ранжированные значения признака, а по оси ординат наносится шкала частот. Полученные точки графика соединяют прямыми линиями, в результате чего и получают полигональную кривую. При построении гистограммы для дискретных чисел приращения по оси абсцисс делят пополам и вместо кривой выстраивают прямоугольники, в которых центральная линия, делящая прямоугольники пополам указывает на значение случайной величины, по ординате (высота прямоугольника) выставляется – количество встреч этого значения в выборке или в совокупности.
Полигональные кривые используются в большей мере при изображении распределений дискретных величин. Для построения полигональной кривой по оси абсцисс откладывают ранжированные значения признака, а по оси ординат наносится шкала частот. Полученные точки графика соединяют прямыми линиями, в результате чего и получают полигональную кривую. При построении гистограммы для дискретных чисел приращения по оси абсцисс делят пополам и вместо кривой выстраивают прямоугольники, в которых центральная линия, делящая прямоугольники пополам указывает на значение случайной величины, по ординате (высота прямоугольника) выставляется – количество встреч этого значения в выборке или в совокупности.
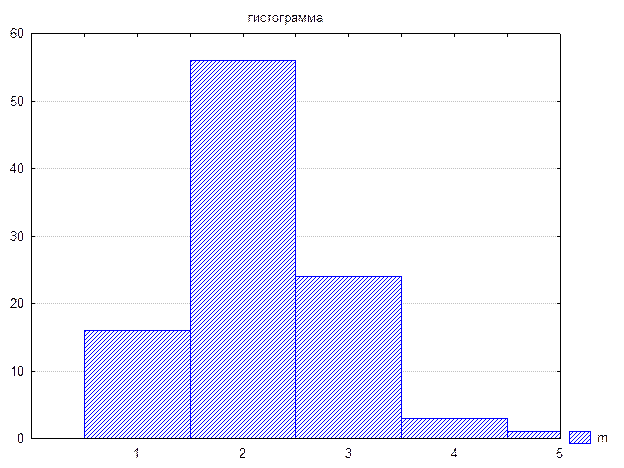
При создании таблицы и построения гистограммы для непрерывной случайной величины ее значения делят на ряд равных или не равных по величине интервалов (классов или групп), которые откладывают по оси абсцисс, а по оси ординат откладывают количество величин, попавших в конкретный интервал. Величины, попавшие в выборку или совокупность, часто объединяются в группы с какой либо целью, так на рудных месторождениях полезные компоненты часто разделяются на бедные, богатые, наиболее богатые, сверхбогатые (например, самородки золота) или по технологическим признакам, например легкообогатимые, обогатимые и труднообогатимые.
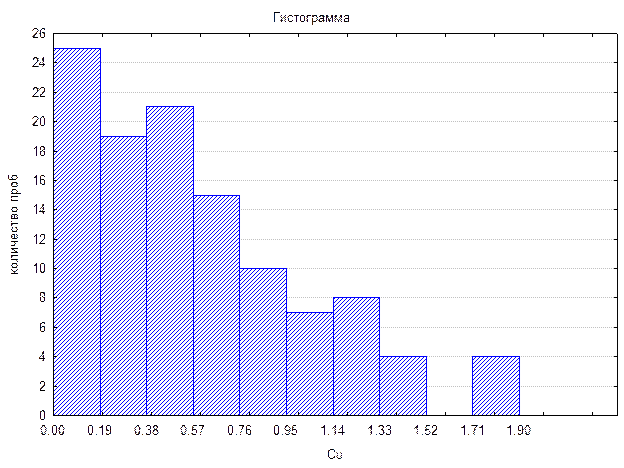 Такие ряды распределения называют атрибутивными, то есть построенными по качественным признакам. В таких случаях нередко значения признака группируют не на равные интервалы. Если группировка построена просто по количественному признаку, то она называется вариационной, любой вариационный ряд состоит из вариантов и частот. Вариантами называют отдельные значения признака, частоты – это количество вариантов или значений признака в каждой группе ряда. Частостями называют частоты, выраженные в долях единицы или в процентах к итогу частот. Для сравнения частот вводится понятие плотности распределения – это частота, рассчитанная на ширину интервала. От группировок следует различать классификации. Отличительной чертой классификаций является то, что группирование в них происходит на основании систематизации признаков. Классификации утверждаются и признаются международными или государственными организациями. Например, к классификациям можно отнести классификацию промышленных типов месторождений металлических полезных ископаемых, классификацию углей, классификацию нефтепродуктов, классификации окаменелых органических остатков и так далее.
Такие ряды распределения называют атрибутивными, то есть построенными по качественным признакам. В таких случаях нередко значения признака группируют не на равные интервалы. Если группировка построена просто по количественному признаку, то она называется вариационной, любой вариационный ряд состоит из вариантов и частот. Вариантами называют отдельные значения признака, частоты – это количество вариантов или значений признака в каждой группе ряда. Частостями называют частоты, выраженные в долях единицы или в процентах к итогу частот. Для сравнения частот вводится понятие плотности распределения – это частота, рассчитанная на ширину интервала. От группировок следует различать классификации. Отличительной чертой классификаций является то, что группирование в них происходит на основании систематизации признаков. Классификации утверждаются и признаются международными или государственными организациями. Например, к классификациям можно отнести классификацию промышленных типов месторождений металлических полезных ископаемых, классификацию углей, классификацию нефтепродуктов, классификации окаменелых органических остатков и так далее.
Часто количество интервалов в выборке или совокупности определяют просто по формуле Стерджесса
n = 1 + 3.322 * LgN
где n - число групп, а N - количество значений в выборке. После определения числа групп в выборке можно определить интервалы группировки. Каждый интервал имеет нижнюю и верхнюю границу, и величина интервала определяется как разность между верхней и нижней границей.
Для графического изображения вариационных рядов часто используют кумулятивную гистограмму. При помощи кумулятивной кривой (или кумуляты) отображается ряд накопленных частот, которые рассчитываются путем последовательного суммирования частот по группам. При построении такой кривой по оси абсцисс откладывают значения переменной в виде интервалов, а по оси ординат последовательно накопляемые частоты в виде перпендикулярных столбиков по отношению к оси абсцисс, затем верхние средние точки столбиков соединяют и получают ломаную линию, это и есть кумулятивная кривая. 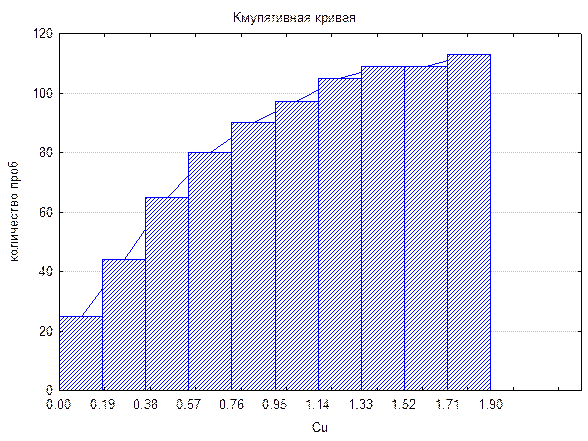
Если при графическом изображении такой гистограммы оси поменять местами, то мы получим кривую, которую называют – огива.
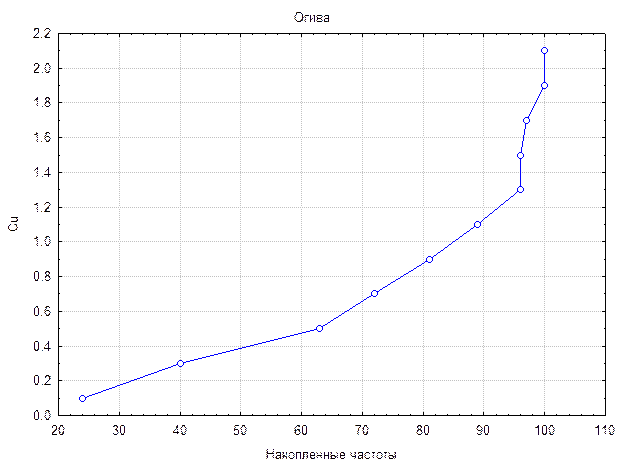
С помощью кумулятивной прямой и огивы могут изображаться процессы накопления, например, накопления прибыли при эксплуатации месторождения за период его жизнедеятельности или накопления отвалов пустых пород, вынимаемых для того, что бы начать отрабатывать залегающие на глубине рудные залежи.
Таким образом, к графикам распределения случайных величин можно отнести гистограмму, полигональный график, кумулятивный график и огиву.
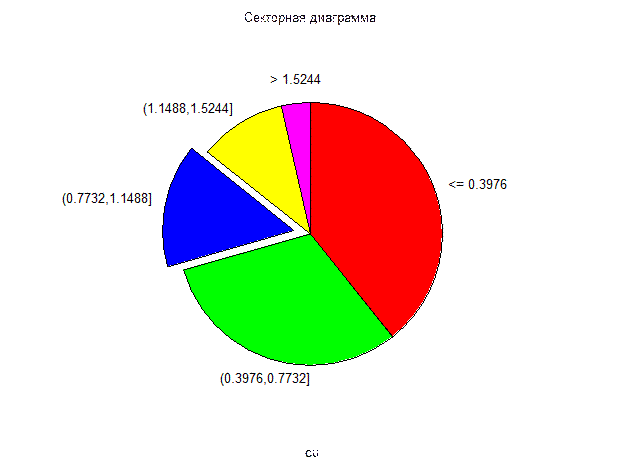
Кроме графиков распределения случайных величин эмпирические данные большого объема можно представлять в виде простых графиков, диаграмм и статистических карт. Среди диаграмм выделяют диаграммы сравнения, структурные диаграммы. Наиболее распространенными среди диаграмм сравнения являются столбиковые диаграммы, среди структурных диаграмм наибольшую популярность имеют круговые секторные диаграммы, несущие ту же информацию, что и гистограммы и реже используются спиральные диаграммы, отражающие нередко сезонные колебания какого-либо признака.
 Статистические карты представляют собой графические изображения распределения данных на геологической или географической карте на определенной территории. Средствами изображения могут быть штриховка, фоновая раскраска, геометрические фигуры или полигональные линии – изолинии (isos – равный, одинаковый подобный). Изолиния это линия одного значения, какого либо параметра, расположенная на карте, разрезе или плане. Изолиниями отражается непрерывное изменение параметра в зависимости от двух других переменных, наиболее часто изолиниями отражается изменение рельефа дневной поверхности территории или скрытой предполагаемой поверхности какого-либо стратиграфического горизонта (кровли или его подошвы), находящегося на большой глубине. В последнем случае положение изолиний обычно предполагается в каждой точке карты или рассчитывается по формулам (интерполируется) на основе редких точек наблюдений за положением кровли или подошвы данного стратиграфического горизонта. Часто изолиниями отражают изменения вредных примесей и полезных компонентов в рудах. С изолиниями тесно связан термин – гридирование (grid), когда изучаемую территорию разбивают на равные прямоугольники или квадраты и отображают изменение изучаемого параметра интерполированными значениями в этих квадратах или прямоугольниках, а затем по этим значениям и отстраивают изолинии.
Статистические карты представляют собой графические изображения распределения данных на геологической или географической карте на определенной территории. Средствами изображения могут быть штриховка, фоновая раскраска, геометрические фигуры или полигональные линии – изолинии (isos – равный, одинаковый подобный). Изолиния это линия одного значения, какого либо параметра, расположенная на карте, разрезе или плане. Изолиниями отражается непрерывное изменение параметра в зависимости от двух других переменных, наиболее часто изолиниями отражается изменение рельефа дневной поверхности территории или скрытой предполагаемой поверхности какого-либо стратиграфического горизонта (кровли или его подошвы), находящегося на большой глубине. В последнем случае положение изолиний обычно предполагается в каждой точке карты или рассчитывается по формулам (интерполируется) на основе редких точек наблюдений за положением кровли или подошвы данного стратиграфического горизонта. Часто изолиниями отражают изменения вредных примесей и полезных компонентов в рудах. С изолиниями тесно связан термин – гридирование (grid), когда изучаемую территорию разбивают на равные прямоугольники или квадраты и отображают изменение изучаемого параметра интерполированными значениями в этих квадратах или прямоугольниках, а затем по этим значениям и отстраивают изолинии.
Лекция 4
Многие математики, начиная с 18 века (Гаусс, Лаплас, Бернулли и другие) стали разрабатывать теоретические модели распределения дискретных случайных величин, используя для этого опыты типа “схемы урн”. Интерес математиков к этим исследованиям был в то время обусловлен развитием в Европе карточных игр. Позднее эти исследования явились отправной точкой развития статистики, которую успешно стали применять почти во всех науках, в том числе и в геологии.
Дата: 2018-12-28, просмотров: 432.