Нормальное распределение непрерывной случайной величины.

Измерения, проводимые на больших выборках, взятых из природных совокупностей, позволяют охарактеризовать самое известное распределение  из всех распределений непрерывной случайной величины. Обычно большая часть значений в этом распределении группируется около некоторого центрального значения, при удалении от которого частоты резко убывают. График частот имеет один максимум, и само распределение называется нормальным распределением случайной непрерывной величины.

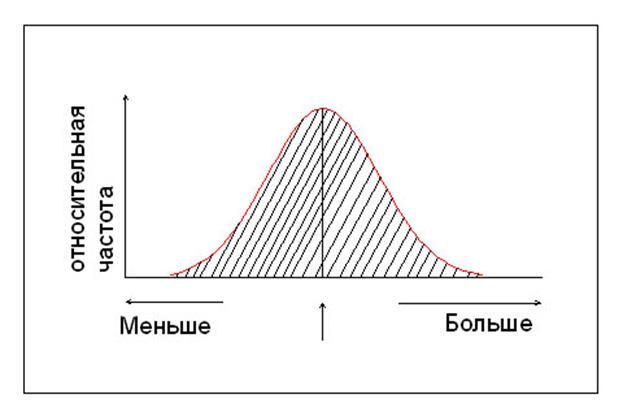
Рис. График нормального распределения случайной величины.

Часто делаются допущения, что если какие либо непрерывные случайные величины распределены нормально, то для их анализа можно использовать большинство статистических критериев, о которых пойдет речь ниже, то есть многие  разработанные статистические критерии основаны на этом допущении. Общая площадь, заключенная между графиком нормального распределения и горизонтальной осью равна 1 (или 100%). Первоначально нормальный закон распределения случайной величины вывел Гаусс в 18 веке. Нормальный закон распределения случайной величины называют еще Гауссовой функцией ошибок, которую он вывел на основе анализа случайных ошибок при наблюдениях природных объектов. Однако в дальнейшем оказалось, что очень много  результатов измерений описываются Гауссовой кривой распределения.

Аналитическое выражение кривой распределения есть дифференциальная функция распределения.

φ(x) = dF(x)/dx

То есть вероятность того, что случайная величина  x примет значение в пределах A< x >B, численно равна площади под кривой распределения, заключенной между ординатами A и B. Поэтому дифференциальную функцию распределения называют плотностью вероятности или плотностью распределения.

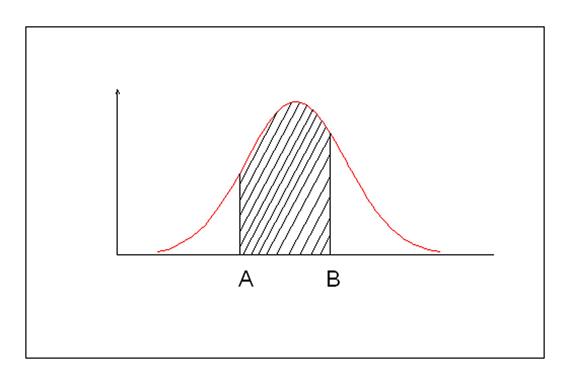
Рис. Плотность вероятности нормального распределения случайной величины.

Нормальное распределение случайной величины имеет ряд характерных свойств.

1. Частоты относительно середины графика располагаются примерно симметрично.

2. Чем меньше по абсолютной величине ошибки, тем чаще они встречаются.

3. Кривая распределения частот похожа на колокол – отмечается резкое падение частот по мере удаления от середины графика и далее постепенное выполаживание кривой.

Нормальное распределение обычно возникает, когда производятся повторные измерения некоторой величины. При каждом индивидуальном измерении возникает множество причин, воздействующих на объект измерения, часто в противоположных направлениях, часть этих воздействий взаимно уничтожается, часть нет, и это все и отображается на колоколообразной кривой нормального распределения.

Параметры и статистики.

Все непрерывные распределения совокупностей имеют ряд характеристик, таких как среднее положение распределения, положения распределения, делящие его на равные части,  мера разброса относительно среднего положения и характеристики симметрии и формы изучаемых кривых распределений. Наиболее удобно проанализировать эти характеристики на примере как раз нормального распределения непрерывной случайной величины. Будем называть эти характеристики параметрами, если они характеризуют совокупность и статистиками, если они рассчитаны из выборочных данных. Статистики обычно являются оценками параметров изучаемых совокупностей, а сами параметры являются истинными характеристиками изучаемых объектов. Важной особенностью нормального распределения является то, что по плотности распределения или по размеру площади под кривой распределения, заключенной между какими-либо ординатами мы можем оценить величину ошибки при проведении наших измерений.