Теорема сложения вероятностей

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Основы геостатистики.

Лекция N 1.

Применение математических методов в геологии, вероятно, происходило еще многие сотни лет назад, по крайней мере, людям уже очень давно приходилось делать количественную оценку мест рудной минерализации, так как на планете известны места, из которых добывались полезные для людей минералы, еще в доисторическое время.

Однако первые серьезные опубликованные работы по применению математических методов в геологической практике относятся к началу 19 века. Ученый Чарльз Лайель, имея выборочные данные, произвел на основе количественного анализа соотношений различных видов ископаемых раковин стратиграфическое расчленение третичных отложений. В конце 19 века ученые Г.Ниггли и Ф.Ю.Левинсон-Лессинг по результатам математической обработки химических анализов и микроскопических исследований шлифов выделили типы магматических пород.

При поисках и разведке месторождений полезных ископаемых специалисты стали использовать математические методы с начала 20 века. Наибольший вклад в нашей стране в пропаганде использования математических методов при поисках, разведке и оценки месторождений полезных ископаемых внесли Зенков, В.Г.Соловьев, Н.К.Разумовский, Родионов, А.Б.Вистелиус, А.Аренс, Марголин, А.П.Калистов, А.М.Шурыгин, Рыжов, В.М.Гудков, А.Б.Каждан, О.И.Гуськов и другие исследователи.

Среди зарубежных исследователей можно отметить Д.Криге, Карлье, У.Крамбейна, Т.Лаудона и много других исследователей. Особенно нужно отметить работы Ж.Матерона и Д.Давида, разработавших методы оценки и подсчета запасов месторождений полезных ископаемых, которые сейчас внедрены во все современные программные продукты, используемые для трехмерного моделирования месторождений и подсчета запасов и так же фундаментальный труд Дж.С.Девиса, который в конце прошлого века в своей работе описал все математические методы, когда либо использованные в геологии.

Уже, начиная с 60-х годов 20 века, вычислительные машины стали широко применяться в университетах, научно-исследовательских организациях и производственных объединениях. Геологи стали значительно чаще прибегать к использованию математического анализа первичных данных, поставляемых из пунктов наблюдений, несмотря на то что, методы математического анализа были разработаны для других наук и не разу не использовались до этого в геологии. Однако разработанные геологами математические правила построения карт, геологических разрезов, графиков, правил оконтуривания скоплений ценных минералов привели к прогрессу также и в других науках.

Повсеместное внедрение математических методов в геологии стало возможных с конца 20 века, когда снизилась стоимость персональных компьютеров и компьютеры стали доступны практически для каждого геолога. Одновременно с начала 80-х годов 20 века частные компании стали выбрасывать на рынок значительное количество компьютерных программ, написанных нередко специально для решения конкретных задач в различных отраслях, в том числе и геологической отрасли. Сейчас уже создано большое количество таких программ, и многие геологи стремятся использовать эти программы для своей непосредственной работы. Однако чтобы эффективно использовать эти программы нужно хорошо понимать математические приемы и методы, алгоритмизированные в этих программных продуктах. Этот курс лекций посвящен разбору математических количественных методов анализа геологических данных, получаемых в результате поисков, разведки и эксплуатации месторождений полезных ископаемых.

Нередко многие ученые объединяют эти методы в одну науку, которую называют геоматематикой или геостатистикой. В широком смысле статистика это обобщение и наглядное представление эмпирических данных большого объема с возможностью легко сделать выводы из этого обобщения. Статистика позволяет распространить выводы, полученные по ограниченному числу наблюдений на весь изучаемый объект. Ограниченное число наблюдений мы будем называть – выборкой, а весь изучаемый объект – совокупностью. Эти определения основаны на предпосылке, что представление о каком-либо объекте, находящемся на определенной глубине в земной коре можно получить на основе отрывочной информации, получаемой в результате нашего изучения этого объекта по ограниченному количеству или естественных (например, обнажения горных пород) или искусственных (например, буровые скважины или горные выработки) точек наблюдения. Однако при решении этой задачи могут возникнуть разные ситуации, например, когда мы можем проверить наши предположения относительно формы изучаемого природного объекта и когда мы не при каких обстоятельствах этого сделать не можем. Например, когда мы изучаем положение некоторого стратиграфического горизонта на территории крупного сегмента земной коры, например, платформы, никто не будет бурить бесчисленное количество скважин, чтобы получить истинное представление о залегании этого стратиграфического горизонта в земной коре, как бы это важно не было для развития науки. Поэтому многие выдвигаемые геологами представления, гипотезы нельзя проверить. Тем не менее, при выдвижении и таких гипотез нередко геологи опираются на статистические процедуры, даже если не все формальные требования, которые необходимо соблюдать, были выполнены.

В других случаях очень часто за исследовательскими и поисково-разведочными работами происходит промышленное освоение выявленных месторождений ценных минералов. В этом случае геологи всегда, хотя и с определенной долей условности, могут проверить первоначальные гипотезы относительно формы выявленных объектов и их ценности, так как в результате эксплуатации получают истинное представление об этих объектах. Это не относится к природным процессам, создавшим эти объекты, так как часто эти процессы и после эксплуатации месторождения часто оказываются не понятыми исследователями. Имея истинные представления о форме и ценности объектов, геологи могут рассчитать какое необходимое количество пунктов наблюдения нужно создать, что бы изучив их получить правильное представление об подобных изучаемых природных объектах. К сожалению, особенно на первоначальных стадиях изучения месторождений, геологи берут пробы только там, где это возможно. Проходка горных выработок и бурение скважин может быть не оправдана, пока специалисты не убедятся, что они исследуют природные объекты, содержащие промышленные количества полезных компонентов. Поэтому часто геологи судят, в том числе и о крупных геологических объектах по достаточно ограниченному количеству данных, собранных в пунктах наблюдения и практически всегда этих данных бывает недостаточно для суждений, однако наблюдения геологов слишком важны для развития человеческой цивилизации, чтобы можно было бы их игнорировать. Таким образом, геологи сталкиваются с задачами, в которых они могут контролировать и планировать правильно эксперимент, например, когда они могут рассчитать (хотя бы методом аналогий), какое количество точек наблюдения необходимо иметь для получения достоверной информации об изучаемом объекте. И также геологи сталкиваются с задачами, при решении которых они не могут рассчитать количество точек наблюдения, необходимое для получения достоверной информации об объекте. При этом так называемом неконтролируемом эксперименте многие требования формальной статистики и сами статистические процедуры не работают, и нередко исследователь принимает решения, опираясь на свой опыт и везение.

Нередко свои гипотезы геологи оформляют в виде проекций: - разрезов земной коры, геологических карт, планов подземных горизонтов месторождений и в виде геолого-математических моделей изучаемых объектов. Геолого-математическими моделями можно назвать такие модели природных объектов, в которых отражены не только морфологические особенности строения объектов (форма, мощность, элементы залегания), но и отражены геологические и математические закономерности распределения ведущих признаков этих объектов, изучены их количественные взаимосвязи, установлены природные механизмы, процессы, создавшие изучаемые объекты.

Прежде чем начать излагать сам предмет, который мы назвали геоматематикой или геостатистикой, нужно иметь представление о природе систем чисел, в которых проводятся измерения в пунктах наблюдения. Что такое измерение? Измерение это присваивание некоторой изучаемой характеристике объекта ее величины. Существует четыре шкалы измерений: номинальная, порядковая, интервальная и относительная.

Номинальная шкала измерений основана на присваивании наблюдениям некоторых величин в виде чисел или обозначений, взаимно исключающих друг друга и классифицирующих наблюдения по одинаковым категориям, эти одинаковые категории могут обозначаться цветами, буквами алфавита или цифрами, при чем цифры в этом случае используются только как идентификаторы, отражающие типы объектов. Не обязательно в этом случае, что цифра 2 больше чем цифра 1.

Порядковая шкала измерений подразумевает присваивание наблюдениям чисел иерархическим способом. Классический пример такой шкалы – шкала твердости Мооса. Эта шкала имеет 10 делений, каждая из которых отражает наши представления о твердости минералов, причем, чем выше деление шкалы, тем тверже минералы. Однако различие между истинной твердостью алмаза (9 деление шкалы) и минералами, находящимися на 8 уровне твердости по этой шкале в несколько раз больше, чем различие по твердости между минералами, находящимися соответственно на 1 и 8 уровнях.

В интервальной шкале длина последовательных интервалов - приращений одинакова. Классический пример такой шкалы – температурная шкала Цельсия. Главный недостаток такой шкалы, препятствующий ее широкому внедрению – отсутствие естественного нуля. Начальная точка отсчета, выбранная в ней это точка замерзания воды, из-за чего мы привыкли к такому распространенному понятию как отрицательная температура. Однако мы знаем, что не существуют отрицательные длины предметов или отрицательные концентрации, например золота.

Относительная шкала имеет не только одинаковые приращения между интервалами, но и истинную точку отсчета. Примером является температурная шкала Кельвина, точка 0 по Кельвину обозначает температуру, при которой останавливается молекулярное движение, никакой предмет не может обладать температурой ниже этой точки, так же как не может быть и отрицательной концентрации вещества или отрицательной длины каких либо предметов.

В относительной шкале производится наибольшее, подавляющее количество всех измерений, однако еще не редки случаи использования многими исследователями при измерении и других шкал, типа номинальной или порядковой.

Что же собой представляют статистические процедуры, позволяющие, имея небольшую выборку наиболее правильно давать оценки изучаемым геологическим признакам, описывать математические законы их распределения в пространстве.

В основном эти приемы основаны на теории вероятности и законах распределения некоторых событий в пространстве и во времени.

Что такое событие? Событием называют факт, который в результате опыта может произойти, а может и не произойти. Классическим примером может служить падение монеты гербом вверх. Что такое распределение событий? Например, монета при подбрасывании 10 раз 7 раз упала гербом вверх, и три раза гербом вниз. В геологической практике событием будет являться, например, обнаружение золотоносной кварцевой жилы пятиметровой мощности с помощью небольших горных выработок – копуш, пройденных через 5 метров друг от друга, или обнаружение той же жилы, с помощью копуш, пройденных через 20 метров друг от друга. Естественно можно поставить вопрос, – с какой степенью возможности может произойти это событие, очевидно, что в первом случае это событие более возможно, чем во втором. Теперь рассмотрим понятие – случайность события. Естественно, что падение монеты гербом вверх – это закономерный итог взаимодействия вращающейся монеты и плоскости, а расположение золотоносной кварцевой жилы – закономерный итог геолого-геохимических процессов, проходивших в данном участке земной коры. Случайным является только появление этих событий для нас, так как мы не можем быстро рассчитать скорость вращения монеты в этом опыте, и в случае с появлением золотоносной жилы плохо представляем геологические и геохимические процессы в земной коре формирующие их. Таким образом, появление этих событий мы можем свести к их прогнозу, то есть случайное для нас событие может быть возможным и прогнозируемым, а значит вероятным.

Вероятность события – это численная оценка объективной возможности появления какого-либо события. Понятие вероятности включает в себя некоторую долю неуверенности. Интуитивно мы каждый день имеем дело с вероятностью, например, мы спрашиваем себя, какая будет завтра погода, и с некоторой долей неуверенности отвечаем на этот вопрос. Одним из способов выражения нашей неуверенности или наоборот уверенности является числовая шкала. Обычно принято вероятность выражать от 0 до 1 или от 0% до 100%. Если мы говорим, что вероятность, что завтра будет дождь равна 0%, то это означает, что мы абсолютно уверены, что завтра дождя не будет. И наоборот, если мы говорим, что вероятность, что завтра будет дождь равна 50%, то это означает, что мы абсолютно не уверены, будет завтра дождь или его не будет. Если мы говорим, что вероятность, что завтра будет дождь равна 70%, мы выражаем относительно дождя большую уверенность, чем неуверенность. Наши оценки вероятности появления, какого либо события, например, дождя или золотоносной жилы на конкретном участке могут быть основаны на многих факторах, как на научных данных, так и на наших субъективных ощущениях. Однако в статистике используется подход, в результате которого учитывается появление какого-либо события в предшествующих опытах. То есть прогнозирование дождя или рудоносной жилы может основываться на учете того, сколько было дождливых дней в предыдущем периоде или сколько раз геологи встречали рудоносные жилы в похожих геологических условиях. Такой подход не противоречит научному подходу к решению данной задачи и тем более не противоречит субъективным ощущениям, он просто дополняет и тот и другой способ, так как даже результаты самых точных научных исследований включают некоторую долю неуверенности. В связи с этим понятие вероятности события тесно связано с понятием частота появления события. Частотой появления события может быть количество дождливых дней в прошедшем месяце, количество золоторудных проявлений на какой-либо территории, количество самородков, найденных в ручье и так далее. Несовместными называют события, которые не могут появиться одновременно в данном опыте, например одновременное падение монеты гербом вверх и гербом вниз, или одновременное появление хорошей и плохой погоды или одновременное обнаружение и не обнаружение рудоносной жилы. Равновозможными называют такие события, вероятность появления которых в данном опыте одинакова, например, при подбрасывании монета может упасть гербом вверх и так же гербом вниз.

События, образующие группу равновозможных и несовместных событий называют случаями.

Когда мы проводим опыты, в результате которых появляются равновозможные и несовместные события, мы можем сказать, что наш опыт проходит по “схеме случаев” или “по схеме урны”. В таких опытах вероятность (P) некоторого события (B) оценивается по относительной доле благоприятных случаев.

P(B)=M/N

Где М – это число опытов, в которых появилось событие B, N- это общее число опытов.

Пример. В урне 10 шаров, из них 3 черных и 7 белых, шары в урне перемешаны и на ощупь не различимы. Какова вероятность события, при котором появляется черный шар. Общее число опытов может быть равно 10. Следовательно, мы десять раз, не глядя, вынимаем шары из урны и, следовательно, вероятность появления черного шара равна 0.3.

P(B)=3/10

В опыте “по схемы урны” хорошо раскрывается понятие “частоты или частности появления события”. Например, если в этом примере несколько изменить условие проведения опыта, например, если вынимать из урны по одному шару, отмечать его цвет, снова класть в урну и после перемешивать шары, то возможно, что черный шар появится в 9 случаях из 10 опытов. В другой серии опытов мы вытащим черный шар только один раз. Всегда частота появления какого-либо события – это так же отношение числа опытов М, в которых появилось событие (В) к общему числу произведенных опытов N.

P=M/N

Частота события имеет случайный характер. Но если мы значительно увеличим число опытов, например, будем тысячу раз вынимать шары из урны, отмечать их цвет, класть обратно и перемешивать, то частота появления черного шара будет незначительно отличаться от 0.3, при чем тем меньше, чем больше будет число опытов.

Устойчивость частоты при большом количестве проведения опытов N является характерным свойством случайных событий. При возрастании числа опытов частота появления какого-либо события всегда приближается к вероятности (теорема Бернулли).

Лекция N2 .

Основные теоремы теории вероятности.

Теорема полной вероятности.

Формула полной вероятности является следствием теорем сложения и умножения вероятностей.

Ниже приведены результаты опробования горизонтальной выработки (канавы), разделенной на три равных участка.

N пробы	Содержание (%)	N пробы	Содержание (%)	N пробы	Содержание (%)
Участок 1		Участок 2		Участок 3
1	8	1	6	1	4
2	4	2	1	2	7
3	3	3	4	3	4
4	8	4	6	4	7
5	4	5	4	5	4
6	3	6	1	6	4
7	8	7	1	7	7

Теперь мы можем переделать эту таблицу как частотную таблицу, в которой рассчитана частота появления пробы с определенным содержанием.

Участок канавы	Содержание металла (%)	Число проб	Частость
Участок канавы N1 (К1)	8	3	0.428
	4	2	0.286
	3	2	0.286
Сумма		7	1
Участок канавы N2 (К2)	6	2	0.285
	4	2	0.285
	1	3	0.430
Сумма		7	1
Участок N3 (К3)	7	3	0.428
Участок N3 (К3)	4	4	0.572
Сумма		7	1

На одном из участков берут пробу, причем участок и место, где берут пробу, выбирают случайно. Случайный отбор может происходить с использованием разных способов, один из них можно назвать способом урны. Сначала скатывают в трубочки листки бумаги с написанными на них номерами канав, кладут в урну, перемешивают и затем выбирают, далее тем же образом приготавливают 7 листков бумаги с предварительно написанными на них содержаниями металла и выбирают из урны один листок.

Вопрос. Какая вероятность появления пробы с содержанием 4%?

Появление события B (то есть появление пробы с содержанием 4%) может произойти только вместе с одним из событий К1, К2, К3 - то есть, появление события В может произойти только в одном из трех участков нашей канавы. События К1, К2, К3 образуют полную группу несовместных событий (событий, которые не могут появиться одновременно в данном опыте), но то что одно из этих событий произойдет в данном опыте равно 100% . Назовем эти события – гипотезами.

Вероятность события В определяется как сумма произведений вероятностей каждой гипотезы на вероятность события при этой гипотезе по следующей формуле

P(B) = ∑ P(Ki)*P(B/Ki)

Это формула полной вероятности. Событие B может появиться только в комбинации с одной из гипотез К1, К2, К3, образующих полную группу несовместных событий. Комбинации К1В, К2В, К3В так же несовместны, так как несовместны гипотезы К1, К2, К3. Применяя к данным комбинациям (гипотезы-события) теорему сложения получим

P(B) = P(B/K1) + P(B/K2) + P(B/K3) = ∑P(B/Ki)

Далее применим теорему умножения и получим

P(Ki, B) = P(Ki)*P(B/Ki)

Поэтому

P(B) = ∑ P(Ki)*P(B/Ki)

По условию задачи гипотезы К1, К2, К3 - равновозможные, следовательно

P(K1) = P(K2) = P(K3) = 0.33

Следовательно легко можно рассчитать, что вероятность появления события В ( то есть вероятность появления пробы с содержанием 4 %) равна

P(B) = P(4%) = 0.33*0.285 + 0.33*0.285 + 0.33*0.572 = 0.38

Таким образом, наугад взятая в канаве проба с вероятность 38% покажет содержание металла равное 4 % .

Такая же вероятность получится, если мы рассчитаем ее по простой формуле, однако, если гипотезы не равны друг другу, то есть например, длина участков будет разная, а количество проб то же, то по простой формуле вероятности мы уже не получим этот же результат.

Лекция 3

Лекция 4

Многие математики, начиная с 18 века (Гаусс, Лаплас, Бернулли и другие) стали разрабатывать теоретические модели распределения дискретных случайных величин, используя для этого опыты типа “схемы урн”. Интерес математиков к этим исследованиям был в то время обусловлен развитием в Европе карточных игр. Позднее эти исследования явились отправной точкой развития статистики, которую успешно стали применять почти во всех науках, в том числе и в геологии.

ГГГ ГРГ РРР

ГГР РГГ [ РГР ]

[ГРР] [РРГ]

В скобках находятся комбинации, в которых выпало по одному гербу. Всего возможны три комбинации, в которых выпадает один герб при трех бросаниях или по другому возможны три комбинации с одним успехом в трех следующих друг за другом опытах. Символически это изображается как (ⁿ_r) или n по r, где n – это число опытов, а r – это число успехов. Число комбинаций в n опытах при r успехах легко рассчитать по формуле

n! / r!(n-r)! .

В данном случае

(ⁿ_r) = (³₁) = 3! / 1!*(3-1)! = 3*2*1 / 1*(2*1) = 6 / 2 = 3

Так же по этой формуле можно рассчитать число возможных комбинаций, содержащих 2, 3 или 0 успехов. Напомним, что 0! = 1, а не нулю. Число возможных комбинаций в 2 успехах равно 3, число комбинаций 3 успехов равно 1, и при нуле успехов число комбинаций также равно 1, при общем числе возможных комбинаций равном 8. Обозначим вероятность выпадения герба буквой p, а решки – буквой q, при чем ясно, что q = 1-p.

В этом случае мы можем переписать возможные исходы при трех бросаниях как

p³ p²q q

qp² qp² pq²

q²p q²p

Полную систему событий можно записать как

q³ +3q²p +3p²q +p³ =1 = (q+p)³

Так как по теореме сложения вероятности, верно, то, что любая из этих комбинаций обязательно произойдет, то полная вероятность равна 1. Это можно подтвердить и прямым расчетом

0.5³ + 3*0.5² + 3*0.5²*0.5 + 0.5³ = 0.125 + 0.375 + 0.375 + 0.125 = 1

Так как вероятности p и q являются членами бинома Ньютона, то и это распределение получило название биноминального распределения. Так как конкретное число комбинаций рассчитывается по формуле n! / r!(n-r)!, то общую формулу биноминального распределения можно написать как

P(n) = n!/r!(n-r)! *( p^r* qⁿ^-r).

Эксперимент с бросанием монеты имеет три особенности:

1. В каждом испытании имеется только два возможных исхода – успех и неудача.

2. Исход каждого испытания не зависит от предыдущих исходов, и вероятность успеха остается постоянной.

3. Испытания повторяются заданное число раз.

Распределение вероятностей, соответствующее указанному типу экспериментов называется биноминальным распределением.

В качестве примера можно назвать предсказание успеха при бурении поисковых скважин, предназначенных для обнаружения какого-либо полезного ископаемого – нефти, газа, золота, железной руды и так далее.

Каждое испытание или бурение каждой скважины может быть классифицировано как “открытие” (успех), либо как “пустая скважина” (неудача). Успех или неудача при бурении каждой последовательной скважины не зависит от предыдущих результатов бурения, так же как и решение продолжать или не продолжать бурить. Число скважин ограничено денежными средствами, выделяемыми корпорациями или государством в конкретный период времени для поисков на данной территории. В данном случае биноминальное распределение будет подходящим для расчета вероятности успеха, то, есть для расчета вероятности открытия новых объектов, имея ограниченное количество средств. За вероятность открытия новых залежей на прогнозируемой территории могут приниматься субъективные оценки, научные разработки. Однако мы уже знаем, что в статистике используется подход, рассматривающий появление какого-либо события в предшествующем опыте. То есть прогнозирование новых залежей полезных ископаемых должно исходить из анализа, сколько раз были встречены новые залежи в похожих геологических условиях. Такой подход не противоречит научному подходу, он просто его дополняет, так как даже самые продвинутые научные достижения все равно включают некоторую долю неуверенности. Вероятность того, что при бурении на прогнозируемой территории среди n скважин (общего запланированного количества скважин) будет r успешных скважин можно рассчитать по формуле

P(r) = [n!/(r!*(n-r)!)] *( p^r* qⁿ^-^r).

Предположим, что мы хотим рассчитать вероятность успеха программы поисково-разведочных работ, включающей бурение 5 глубоких скважин на территории, хорошо изученной специалистами-геологами и научными работниками и выдвинувших смелые гипотезы о рудоносности конкретных тектономагматических структур, широко развитых на данной территории. Однако не смотря на то что уже доказано, что подобные структуры являются рудоносными, промышленные объекты были выявлены только в одном районе из десяти, в которых проводились поисково-разведочные работы, то есть вероятность успеха – обнаружение промышленных залежей полезных ископаемых в новом одиннадцатом районе равна 10%.

Какая вероятность того, что вся программа, включающая бурение только 5 скважин будет полностью провалена. В этом случае в биноминальное уравнение мы будем подставлять общее количество опытов n = 5, а число успехов r = 0, вероятность p = 0.1.

Тогда вероятность того, что в результате поисково-разведочных работ не одна из скважин не встретит залежь можно легко рассчитать, как

P (r) = (5!/5!*0!)*1*0.9⁵ = 1*1*0.59 = 0.59.

В этом случае вероятность полного провала данной программы будет составлять около 60%.

Какова вероятность, того, что одна из заявленных скважин подсечет залежь с промышленными содержаниями полезного компонента. В этом случае в биноминальное уравнение мы будем подставлять общее количество опытов n = 5, а число успехов r = 1, вероятность p = 0.1.

Тогда вероятность того, что в результате поисково-разведочных работ одна из скважин вскроет залежь можно легко рассчитать, как

P (r) = (5!/4!*1) *0.1 * 0.9⁴= 5*0.1*0.25 = 0.328.

В этом случае вероятность успеха будет составлять около 33%. Используя либо уравнение или таблицу биноминального распределения, она опубликована во многих учебных пособиях по статистике, легко найти вероятности всех возможных исходов в данной программе, включающей бурение только 5 скважин. Ясно, что увеличение количества скважин в данном проекте приведет к увеличению вероятности успешного его завершения. Приведенные расчеты могут быть весьма полезными для горнорудных корпораций или геологоразведочных компаний при составлении планов бурения на прогнозных территориях. Нужно добавить, что этот способ имеет еще одну очень важную особенность, скважины в пределах предполагаемых рудоносных структур должны располагаться случайным образом, отсюда этот способ расположения скважин для наилучшего достижения результата на изучаемой территории получил название метода дикой кошки (здесь подразумевается, что невозможно спрогнозировать направление каждого шага дикой кошки). Метод дикой кошки не противоречит научному подходу к решению данной проблемы, так как даже самые современные методы поисков и разведки и самые продвинутые научные гипотезы не позволяют определить точное положение залежей полезных ископаемых в земной коре, они могут только значительно сузить радиус поисков.

Лекция 5.

Дискретные распределения мы рассматривали в основном при фиксированном количестве испытаний, так в случае биноминального распределения мы считали, как распределяются вероятности комбинаций гербов и не гербов при трех бросаниях монеты, а что произойдет, если мы увеличим количество испытаний. Можно рассчитать вероятность заданного количества успехов (например, гербов) в 10, 15, 25, 50 бросаниях монеты. Эти вероятности давно рассчитаны и находятся в таблицах биноминального распределения, но так же легко они могут быть вычисленными на калькуляторе или при помощи небольшой компьютерной программы. Однако, при любом количестве испытаний, любая из возможных комбинаций обязательно осуществится на все 100%, поэтому площадь под графиком распределения всегда будет равна 1. А если число бросаний будет увеличиваться, то ширина столбиков будет все меньше и меньше и, в конце концов, вместо столбиков гистограмму можно изобразить плавной непрерывной кривой. В эксперименте бросания монеты мы имеем дело с дискретными исходами эксперимента, однако, в большинстве экспериментов на природных объектах, результаты не являются дискретными. В этом случае, как отмечалось ранее, при подсчете частот учитываются не отдельные значения, а количество чисел, попадающих в намеченные интервалы. Еще одно важное отличие дискретных величин от непрерывных, это то, что дискретные величины можно измерить с абсолютной точностью в отличие от непрерывных величин. В первую очередь это связано с тем, что при измерении свойств у природных объектов в подавляющем большинстве используются приборы, в которых уже заложены ограничения точности измерения, мы знаем, что чем совершеннее прибор, тем выше точность измерения, произведенная им. При повторных измерениях одного и того же свойства природного объекта всегда возникают отклонения малой величины, однако они связаны не только с точностью измерения прибором, но и с изменениями в условии проведения самого эксперимента, а также и с изменчивостью самого измеряемого природного объекта. Никогда не может быть получено единственное, точное истинное значение свойства природного объекта, всегда мы будем наблюдать непрерывное распределение возможных значений этого свойства, что как раз характерно для непрерывных случайных величин. Изменчивость, обусловленная неточностью конкретного прибора, с помощью которого мы производим измерения, возникает, когда делаются повторные измерения на абсолютно том же объекте без каких либо изменений в проведении опыта. Такую изменчивость объясняют и называют ошибками эксперимента или ошибками регистрации. Однако на практике все причины изменчивости проявляются сразу и отражаются в результатах измерений так, что нельзя отличить в силу каких причин данные изменения возникли, или в силу ошибки при измерении прибором, или в силу изменившихся условий эксперимента или в силу природной изменчивости измеряемого свойства. Оценить природную изменчивость по данному измеряемому свойству можно, когда измерения проводятся не на абсолютно том же объекте. Предположим, что мы обладаем столбиком керна некоторой длины (керн это каменный материал, поднятый из скважины). Мы хотим определить проницаемость данного материала, но не можем ввести для измерения проницаемости в прибор весь керн. Вместо этого мы вырезаем из керна несколько пластинок и измеряем проницаемость в каждой из них. Полученный результат и наблюдаемая изменчивость будет обусловлена природной изменчивостью керна, меняющимися условиями эксперимента и ошибкой измерения.

Еще раз остановимся на двух таких важных понятиях как “выборка” и “совокупность”. Совокупность представляет собой множество (либо конечных, либо бесконечных) элементов. Выборка – это подмножество элементов, выбранных из некоторой совокупности. В классических учебниках статистики часто используют термины – выборочная совокупность и генеральная совокупность, что идентично терминам просто выборка и совокупность. Измерения проницаемости, которые мы осуществили, были проведены по выборке образцов взятых из некоторой природной совокупности и те результаты, которые мы получили, являются оценками истинной проницаемости совокупности или изучаемых природных объектов. Обычно выборочные образцы из природной совокупности должны извлекаться случайным образом, что бы все особенности совокупности были представлены в нашей выборке, однако если исключить из выборки, некоторые образцы, отражающие особенности совокупности то мы получим смещенную выборку. Предположим, если мы не станем измерять проницаемость в пластинах керна не обладающих должной на наш взгляд прочностью, раздробленных и с видимыми порами, то мы получим искаженные представления о проницаемости, данной породы. То есть наши оценки истинной проницаемости природного объекта будут неверными. В статистике выделяются два вида ошибок: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный (непреднамеренный) или систематический (тенденциозный) характер. Ошибки репрезентативности возникают в силу того, что выборка или выборочная совокупность не полностью отражают генеральную совокупность. Избежать ошибок репрезентативности нельзя, но можно установить границы возникновения этих ошибок. Чем больше по количеству измеряемых проб будет наша выборка, тем точнее будут наши оценки свойств совокупности.

Параметры и статистики.

Все непрерывные распределения совокупностей имеют ряд характеристик, таких как среднее положение распределения, положения распределения, делящие его на равные части, мера разброса относительно среднего положения и характеристики симметрии и формы изучаемых кривых распределений. Наиболее удобно проанализировать эти характеристики на примере как раз нормального распределения непрерывной случайной величины. Будем называть эти характеристики параметрами, если они характеризуют совокупность и статистиками, если они рассчитаны из выборочных данных. Статистики обычно являются оценками параметров изучаемых совокупностей, а сами параметры являются истинными характеристиками изучаемых объектов. Важной особенностью нормального распределения является то, что по плотности распределения или по размеру площади под кривой распределения, заключенной между какими-либо ординатами мы можем оценить величину ошибки при проведении наших измерений.

Лекция 6.

Лекция 7

Рассмотрим пример.

На эксплуатационном блоке полиметаллического месторождения были отобраны пробы и получены данные, содержащиеся в таблице.

Данные были получены следующим образом. При подготовке блока к эксплуатации было пробурено 96 вертикальных скважин по квадратной сети 3.5 метра на 3.5 метра. Каждая скважина была опробована по интервалам (длина интервала -1 метр). Большое число равномерно расположенных в блоке проб позволило определить среднее содержание металла в блоке с большой точностью. Блок был разделен на 24 участка, в каждом из которых, оказалось, по 12 проб (4 скважины на 1 участок, 1 скважина содержит по 3 пробы). Общее количество проб равно 288 (24*12 = 288).

Содержание (%)	Частота	Относительная частота (частость)
0 – 0.5	59	0.205
0.5 -1	112	0.389
1 -1.5	64	0.202
1.5 – 2	18	0.062
2 – 2.5	12	0.042
2.5 – 3	8	0.028
3 – 3.5	5	0.017
3.5 – 4	5	0.017
4 – 4.5	2	0.007
4.5 – 5	1	0.004
5 – 5.5	2	0.007
Всего:	288	1.00

На рисунке приведено распределение содержания металла в 288 пробах.

Как видно на рисунке распределение носит асимметричный характер и явно не подчиняется нормальному закону.

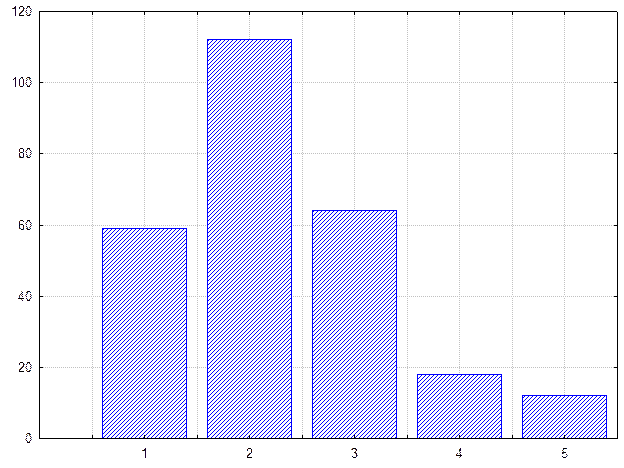
Рис. Гистограмма распределения полезного компонента в эксплуатационном блоке.

Затем было произведено 180 выборок из имеющихся анализов проб. В каждую выборку были случайным образом отобраны из каждого участка по одной пробе. Случайность отбора проб по участкам достигалась при помощи выбора свернутого листка с номером пробы из урны из общего количества свернутых листочков, равного количеству проб на участке. Для каждой выборки рассчитывалось среднее содержание металла, то есть в результате были получены 180 выборочных средних значений. Распределение выборочных средних значений по эксплуатационному блоку приведено в таблице и на рисунке.

Содержание (выборочное среднее)	Частота	Относительная частота (Частость)
0.7 – 0.8	3	0.017
0.8 – 0.9	13	0.072
0.9 – 1.0	30	0.167
1.0 – 1.1	40	0.222
1.1 – 1.2	41	0.228
1.2 – 1.3	31	0.172
1.3 – 1.4	16	0.089
1.4 – 1.5	5	0.028
1.5 – 1.6	1	0.005
Всего	180	1.0

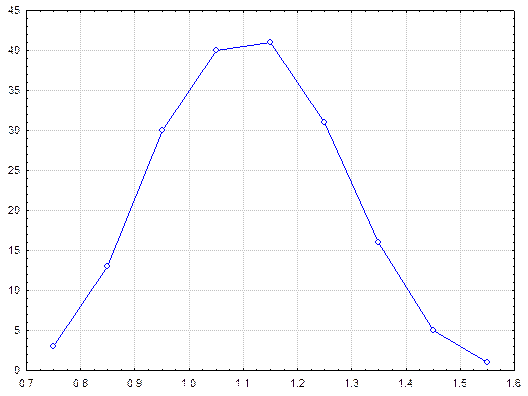
Рис. Распределение выборочного среднего значения по блоку.

Кривая распределения выборочного среднего значения похожа на колокол, причем среднеарифметическое всех выборочных средних значений равно 1.1, что соответствует среднему содержанию металла в блоке, которое как было уже указано выше, определено с большой точностью. Как видно из рисунка распределение выборочных средних значений соответствует или близко к нормальному распределению, хотя распределение просто полезного компонента имеет ярко выраженный асимметричный характер. Используя данные последней таблицы можно вычислить вероятность взятия пробы с некоторым содержанием или плотность вероятности, то есть вычислить вероятность взятия образца определенного класса. По данным второй таблицы вычисляем среднее и стандартное отклонение выборочных средних значений (χ = 1.11, а S = 0.159), а после для нижних границ по каждому интервалу вычисляем параметр u и получаем стандартизированные данные, у которых среднее арифметическое равно 0, а стандартное отклонение равно 1.

U₁ = (0.8 – 1.11)/0.159 = -1.95

Далее берем таблицы вероятности нормального распределения и для u₁ находим по таблице φ(x), в этом случае φ(x) = 0.026. Это также означает, что площадь части совокупности под кривой распределения, если смотреть по абсциссе, от минус бесконечности до значения u (u=-1.95), равна 0.026. Также вычисляем вероятности для класса, например для класса 0.8 – 0.9.

φ(0.8<x>0.9) = φ(u=-1.32) - φ(u=-1.95) = 0.093 – 0.026 = 0.067

То есть мы можем сказать, что с вероятностью 6.7% мы можем взять на месторождении пробу с содержанием от 0.8% до 0.9% данного металла.

Тот же самый результат мы получим, если расчеты будем делать не по таблице, а по формуле

φ(x) = [1/ √2π]*e^-(^u^*^u^)/2.

Если мы, используя формулу или таблицу вероятностей нормального распределения, рассчитаем вероятности для всех значений u, то увидим, что они близки к частостям последней таблицы по классам, из чего можно сделать вывод, что распределение наших эмпирических данных соответствует нормальному распределению.

Обычно мы не знаем, из какой совокупности мы берем выборку, но очень часто подозреваем, что изучаемая совокупность явно значительно отличается от нормальной совокупности. Эти подозрения обычно обусловлены сильно выраженными геологическими процессами, проявившимися на конкретном месторождении. Нужно отметить, все случайные величины, которые мы получаем в результате измерений, делятся на стохастические и детерминированные величины.

Стохастические случайные величины изучаемых признаков характерны для обычных спокойных, длительных во времени геологических и геохимических процессов. Обычно распределение стохастических величин подчиняется нормальному закону распределения.

Детерминированные величины возникают в результате определенных направленных процессов в земной коре, например приводящих к аномально высоким концентрациям химических элементов на локальных участках, которые потом нередко определяются геологами как промышленные скопления полезных компонентов. Теоретически детерминированные изменения природных объектов могут быть описаны средствами точных наук - физики, химии и математики, но практически тектонические и геохимические процессы в большей части очень сложны для понимания и описываются геологами на уровне гипотез. В большей части случаев стохастические, и детерминированные величины перемешаны между собой. Распределение этих перемешанных величин может подчиняться нормальному закону распределения, но больше всего распределения этих величин имеют ярко выраженный асимметричный характер.

Согласно классификации Пирсона можно выделить три типа данных, которые имеют три соответствующих типа распределений. К первому типу относятся данные, имеющие симметричное нормальное распределение, ко второму типу относятся данные, которые после математических преобразований будут иметь нормальное распределение и к третьему типу относятся данные, которые при любых преобразованиях не будут иметь нормальное распределение.

Лекция 8.

Учет ураганных проб.

Сама проблема ураганных проб предполагает две стадии ее решения, в первую стадию, нужно выявить ураганные пробы, а во вторую стадию их нейтрализовать. Существует много способов регистрации ураганных проб, и они подробно описаны в специализированной литературе [ 5 ]. Однако в последнее время среди специалистов наибольшую популярность получили “квантильный” способ обнаружения ураганных значений металлов в пробах и способ обнаружения ураганных проб по излому на кумулятивной кривой распределения, описанные в книге Ю.Е. Капутина “Горные компьютерные технологии и геостатистика”. Если придерживаться терминологии предложенной в этих лекциях, то первый способ можно назвать децильным способом, так как массив проб сначала сортируется по величине содержания металла от минимального до максимального, затем строится частотная таблица и гистограмма. А после таблица разделяется на заданное количество квантилей, обычно на 10 частей (то есть массив разделяется на децили). В результате формируется таблица, пример которой приведен ниже.

Класс	Число записей	Среднее значение	Минимум	Максимум	Доля металла с данным содержанием от всей выборки	Доля металла с данным содержанием от всей выборки (%)
0-10	1110	0.004	0.000	0.010	4.805	0.07%
10-20	1110	0.010	0.010	0.018	11.522	0.16%
20-30	1110	0.021	0.018	0.030	23.816	0.34%
30-40	1110	0.035	0.030	0.049	38.823	0.55%
40-50	1110	0.052	0.049	0.060	57.571	0.82%
50-60	1110	0.080	0.060	0.100	88.946	1.27%
60-70	1110	0.128	0.100	0.160	141.922	2.02%
70-80	1110	0.219	0.160	0.290	243.590	3.47%
80-90	1110	0.426	0.290	0.640	472.534	6.73%
90-100	1106	5.370	0.640	305.310	5938.771	84.57%
ВСЕГО	11096	0.633	0.000	305.310	7022.301	100.00%
90-91	111	0.677	0.640	0.720	75.161	1.27%
91-92	111	0.777	0.720	0.840	86.204	1.45%
92-93	111	0.896	0.840	0.950	99.474	1.67%
93-94	111	1.029	0.950	1.120	114.198	1.92%
94-95	111	1.238	1.120	1.390	137.390	2.31%
95-96	111	1.587	1.390	1.790	176.153	2.97%
96-97	111	2.046	1.790	2.350	227.100	3.82%
97-98	111	2.899	2.360	3.690	321.840	5.42%
98-99	111	5.497	3.700	8.660	610.180	10.27%
99-100	107	38.234	8.670	305.310	4091.070	68.89%
ВСЕГО	1106	5.370	0.640	305.310	5938.770	100.00%

Если последний класс (90-100%) содержит долю металла, большую чем 40% от общего количества, то считается, что в массиве данных существуют ураганные пробы. Далее рассчитывается аналогичная таблица для последнего класса. Границей для ураганных проб считается минимальное содержание первого класса, содержащего долю металла более 10%. В данном примере – это 3.7 г/т. Считается, что подобный анализ нужно проводить для каждого типа руд, и для каждого участка месторождения. На практике отмечается много случаев, когда границы ураганных проб на одном и том же месторождении резко отличались друг от друга на разных его участках.

Второй способ состоит в том, что строится кумулятивное распределение массива данных, но отображается оно в виде огивы и исследуется конечная часть хвоста распределения. На графике отмечается место перегиба кумулятивной кривой, которое и является границей, после которой фиксируются ураганные пробы.

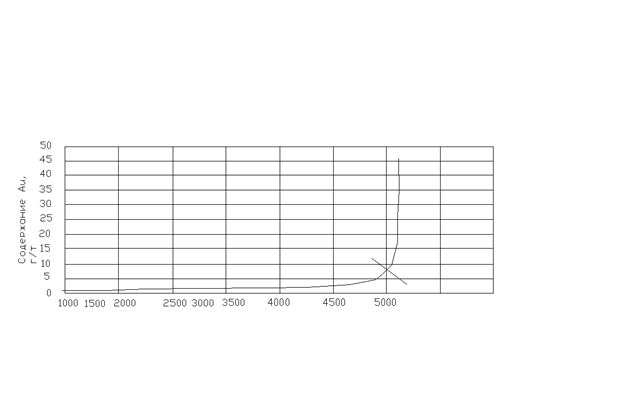
Рис . Определение границы, после которой фиксируются ураганные пробы по месту излома огивы (вместо накопленных частот по оси абсцисс фиксируются соответствующие номера проб).

Существуют еще более простые методы выявления ураганных проб, можно например, просто определить ураганные пробы в хвосте массива распределения, после достижения 95% или 99% накопленных частот или использовать соотношение между модой, медианой и среднеарифметическим значением которое, характерно для умеренно асимметричных кривых -

M_o– χ=3(M_e – χ).

Есть несколько подходов и к нейтрализации ураганных проб.

1. Можно исключить аномальные значения из выборки (например, просто отрезать хвост распределения после достижения 95%-99% накопленных частот).

2. Можно вместо аномальных значений указать пороговые значения, при которых выборочные данные будут иметь нормальное или логнормальное распределение.

3. Можно присвоить аномальным значениям среднеарифметические значения выборки.

Подразумевается, что в первом и третьем случае, после процедур данные будут иметь нормальное или логнормальное распределение. Однако вопрос и о способах выявления и о необходимости нейтрализации ураганных проб остается открытым, так как в любом случае, мы можем допустить еще большую ошибку при оценке истинных параметров, как всей изучаемой совокупности, так и ее частей. Так, например, нейтрализация ураганных проб в выборке, при разведке месторождений золота может уменьшить оценку запасов месторождения, но главное значительно ухудшить экономическую оценку месторождения, из-за высокой цены на этот металл. Тем не менее, большинство специалистов соглашаются, что лучшим выбором для оценки параметров будет выбор нормальной модели распределения выборочных данных. То есть наши оценки параметров будут более точными, чем ближе к нашему экспериментальному распределению будет подходить нормальная модель распределения.

Кроме логарифмирования данных и нейтрализации ураганных проб можно предложить и другие полезные преобразования данных, после которых наши данные могут быть ближе к нормальному распределению. Одно из таких преобразований это преобразование типа - y_i=√x_i и оно в ряде случаев может привести к сокращению пуассоновского хвоста, если наблюдаемые значения близки к 0, то используют преобразование типа - y_i=√x_i +1/2. Можно использовать также и степенные преобразования, в этом случае больше будут увеличиваться большие значения, чем малые, ко всему прочему данное преобразование позволит лучше читать каротажные диаграммы.

Наведенная корреляция.

В некоторых случаях высокие значения коэффициента корреляции между переменными не отражают связь между ними, а возникают вследствие преобразования результатов каких-либо измерений. То есть некоторые независимые случайные величины, полученные путем измерений, имеют нулевую корреляцию, однако некоторые операции над переменными могут привести к возникновению корреляции между ними, хотя как уже было сказано никакой корреляции (или никакого линейного соотношения) между этими переменными не существует. В книге Дж.С.Девиса “Статистический анализ данных в геологии” приводится следующий пример, описанный ниже. Предположим, что образцы гальки случайным образом выбираются на галечном пляже и без перемещения гальки измеряются ортогональные оси (X,Y,Z). Никаких попыток измерить самую длинную ось или самую короткую не предпринимается, измерения проводятся на гальках в том положении, в каком они лежат на пляже. Можно предположить, что результаты измерения по осям будут слабо коррелированы, так как измерения ортогональных осей на больших гальках будут иметь большие значения, по всем трем осям, а на маленьких гальках наоборот измерения будут иметь маленькие значения по всем трем ортогональным осям. В таблице 100 приведены замеры галек и на рисунке 100 показан корреляционный график.

Таблица 100

Номер	Ось 1	Ось 2	Ось 3
1	3	7	8
2	16	5	8
3	10	12	9
4	13	5	12
5	14	16	5
6	9	8	14
7	16	13	13
8	6	3	11
9	9	15	9
10	13	10	9

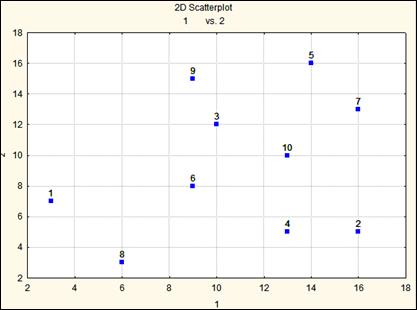
Рис. Слабая корреляция между измерениями первой и второй ортогональных осей. Корреляция равна 0.279.

Однако если изменить положение гальки согласно предварительному соглашению, по которому длинную ось гальки нужно расположить по ортогональной оси X, а короткую ось по ортогональной оси Y, то такое упорядочение приведет к изменению значений измерений и приведет к изменению корреляций. Эти изменения отражены в таблице 100 и на рисунке 100, причем эти изменения могут и не привести к изменению суммы первоначальных измерений размеров галек.

Таблица 100

Номер	x	y	z
1	8	7	3
2	16	8	5
3	12	10	9
4	13	12	5
5	16	14	5
6	14	9	8
7	16	13	13
8	11	6	3
9	15	9	9
10	13	10	9

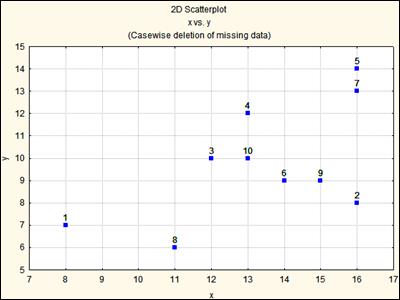
Рис. Корреляция между измерениями первой и второй ортогональных осей (X и Y) равна 0.596.

Анализ рисунка 100 свидетельствует, что упорядочение в измерениях размеров гальки привело к смещению точек на корреляционном графике к нижнему сектору диаграммы, разделенной прямой под углом 45⁰.

Наведенные корреляции, которые причиняют наибольшие беспокойства - это ложные отрицательные корреляции, которые появляются в замкнутых множествах данных. Замкнутым множеством данных называют множество данных, в котором сумма всех переменных равна 100% или 1, что означает, что переменные представляют собой определенные пропорции от целого. Так как сумма переменных есть фиксированное число, то увеличение доли одной переменной приводит к сокращению доли других переменных. В открытом множестве, в котором измерения не представляются в виде пропорций двух независимых переменных, не будет существовать корреляции. Если же открытое множество данных замкнуть преобразованием измерений в пропорции, то появятся отрицательные корреляции, хотя исходные данные первоначально представляли собой независимые переменные. Такие преобразования первоначально первоначальных данных характерны при нанесении данных на треугольные диаграммы, например трехфазные компонентные диаграммы.

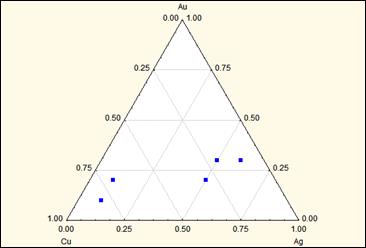
Рис. Пример треугольной диаграммы.

Эти отрицательные корреляции возникают из того факта, что по мере увеличения пропорций одного компонента, остальные два компонента – их значения должны уменьшаться. Так как таких примеров анализа по треугольным диаграммам очень много, то было предпринято много попыток правильно определять в таких данных статистические корреляционные связи, и в настоящее время нет вполне удовлетворительного метода вычисления силы связи между переменными в замкнутых множествах данных. В некоторых случаях в замкнутых таблицах для трех переменных корреляции оцениваются через дисперсии по формуле –

r_1-2=S²₃ – (S²₁+S²₂)/2S₁*S₂

Корреляционный критерий.

Коэффициент корреляции является стандартизированной мерой линейной связи между переменными, но какая статистическая значимость этого коэффициента. Под статистической значимостью мы понимаем, насколько оценка корреляции по выборке соответствует истинному коэффициенту корреляции, вычисленному по совокупности. Коэффициент выборочной корреляции - r является оценкой параметра R, который отражает связь между переменными в совокупности. Предполагая, что обе переменные имеют нормальное распределение, и наши наблюдения выбраны случайно из некоторой совокупности, мы можем осуществить проверку значимости – r. Из совокупности данных могут быть извлечены различные выборки. Мы проверяем две гипотезы нулевую гипотезу и ее альтернативу.

H₀: R = 0;

H₁: R ≠ 0;

Нулевая гипотеза означает, что истинный коэффициент корреляции равен нулю, в этом случае все возможные выборочные коэффициенты корреляции имеют нормальное распределение, а стандартизированное среднее этих коэффициентов равно нулю. Нулевая гипотеза говорит о том, что две переменные не связаны друг с другом, они независимы и любое ненулевое значение выборочного коэффициента корреляции –r возникает просто из-за случайных флуктуаций при случайном выборе.

Альтернативная гипотеза означает, что истинный коэффициент корреляции не равен нулю, в этом случае все возможные выборочные коэффициенты корреляции не распределяются нормально и стандартизированное среднее этих коэффициентов не равно нулю. Альтернативная гипотеза говорит о том, что две переменные зависят друг от друга, а любое нулевое значение, возникает просто из-за изменений внутри совокупности и случайном выборе из нее данных. Мы проверяем, имеет ли наш выборочный коэффициент нормальное распределение со средним равным нулю, а если выборочные коэффициенты не распределяются нормально, то появляется основание заявлять о значимости выборочного коэффициента корреляции, то есть о том, что выборочный коэффициент корреляции соответствует истинному коэффициенту корреляции и что корреляция между переменными существует.

Рис.№ Пример двухструктурной сферической модели вариограммы.

Расчет надежной вариограммы получается только из данных подчиняющихся нормальному закону распределения, поэтому предварительно перед расчетом вариограмм из выборки нужно убрать все пробы с ураганными значениями и все пробы с минемальными значениями, в этом случае распределение компонента в выборке примет симметричный характер. Перед интерполяцией все убранные значения нужно вернуть в выборку.

Кригинг . Предпосылкой развития геостатистических методов послужило расхождение между содержаниями многих металлов в разведочных пробах и реально извлекаемых объемах руд. Точность оценивания зависит от нескольких факторов, количества проб и их значений, расположения проб по месторождению (здесь важна равномерность мест опробования), расстоянием между пробами и точкой в середине оцениваемого блока, наличие пространственной непрерывности рассматриваемой переменной (легче оценить величину регулярной переменной, чем той, которая меняется произвольно). Кригинг – метод интерполяции, который учитывает все эти факторы, был придуман южноафриканским горным инженером Дени Криге и потом усовершенствован Джорджем Матероном. В большинстве методов интерполяции, сначала задается диаметр поискового круга (или эллипса). Все точки, попавшие в поисковый круг, используются для расчета взвешенного среднего, которое будет приписано середине элементарного блока. Веса, с которыми будут учитываться исходные точки, в той или иной мере, зависят от расстояния от узла до этой точки. Разные методы интерполяции – это разные способы взвешивания исходных данных в зависимости от расстояния. В кригинге, как методе интерполяции, взвешивание производится, пожалуй, сложнее, чем во всех других методах. Допустим, что в наш поисковый круг попали несколько проб. Расстояния между пробами и расстояния между серединой оцениваемого блока или его краями используется для снятия вариограмных значений с модельной вариограммы. Затем вариограмные значения заносятся в матрицы системы линейных уравнений, и рассчитываются коэффициенты уравнений, которые и являются весами значений компонента в пробах. После рассчитывается оценка элементарного блока блоковой модели рудной залежи. При решении способом, выбранным Ж. Матероном, появляется небольшое по величине число μ – множитель Лагранжа. Чем множитель меньше, тем лучше решена система линейных уравнений.

Кригинговая оценка рассчитывается по формуле:

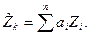
Здесь - кригинговая интерполяционная оценка изучаемой переменной, а 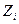- значения переменной в n точках, попавших в круг поиска, 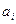-веса. Обычно же, на практике, в поисковый круг попадает несколько десятков или сотен окружающих проб. Соответственно и матричное уравнение расширяется до сотен строк и столбцов.

Считается, что кригинг – это интерполяционная процедура, дающая оценки с наименьшей дисперсией. Дисперсия кригинга равна

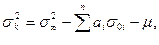
где - порог; 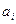- коэффициенты (веса) кригинга; 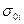- ковариация между точкой оценивания и i-ой точкой; μ – множитель Лагранжа.

Чем меньше дисперсия кригинга по сравнению с общей дисперсией, тем лучше качество полученной оценки.

Точечный или ординарный кригинг рассчитывается для 8 точек, простой кригинг для одной точки.

В последнее время появились работы (Кумбс), в которых исследуется, как можно с помощью вариограммы оценить степень достоверности ресурсов. Выводы о связи размеров зоны влияния с степенью достоверности оценки компонента в элементарном блоке блочной модели напрямую связаны с тем, что вариограмма является обратной автокорреляционной функцией, поэтому оценка с помощью значений проб, находящихся на близком расстоянии наиболее достоверна в связи с тем что в данной зоне влияния значения проб имеют между собой высокую корреляцию. В работе Кумбс предложен следующий механизм оценки степени достоверности. Если значение в блоке интерполировано с помощью значений проб, расположенных в части зоны влияния, ограниченной 2/3 расстояния от 0 до порога (sill), то степень достоверности этого блока можно определить по категории оцененных ресурсов (measured). Если значение в блоке интерполировано с помощью проб, расположенных между первой частью зоны влияния и самой зоной влияния, то степень достоверности этого блока можно определить по категории выявленных ресурсов (indicated). И если значение в блоке интерполировано с помощью проб, находящихся за зоной влияния, то степень достоверности этого блока можно определить по категории предполагаемых (прогнозных) ресурсов (inferred). Использование вариограммы для оценки степени достоверности ресурсов в блоковых моделях приведено на рис.№ .

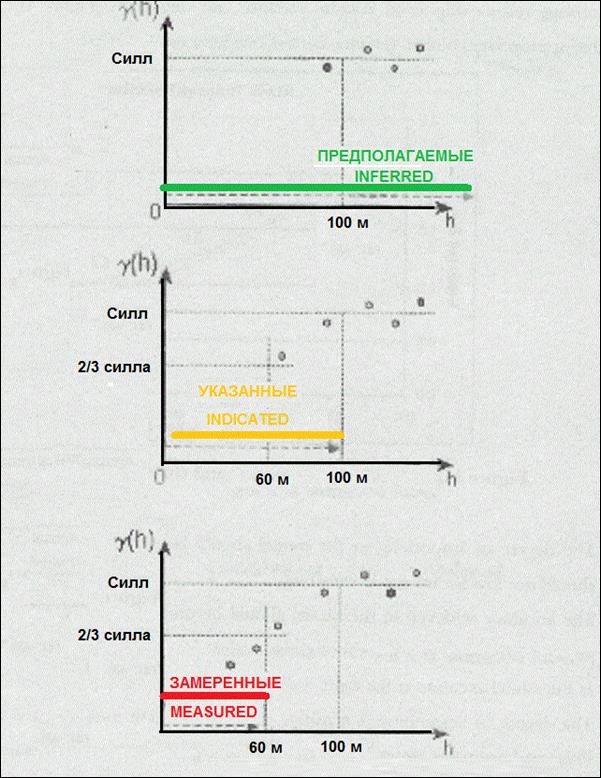
Рис.№ . Использование вариограмм в качестве указателя при классификации ресурсов/запасов.

Основы геостатистики.

Лекция N 1.

События, образующие группу равновозможных и несовместных событий называют случаями.

P(B)=M/N

Где М – это число опытов, в которых появилось событие B, N- это общее число опытов.

P(B)=3/10

P=M/N

Лекция N2 .

Основные теоремы теории вероятности.

Теорема сложения вероятностей.

Если события A,B,C….., несовместны, то есть они не могут появиться одновременно, то вероятность появления любого из них равна сумме вероятностей этих событий.

P (A или В……K) = Р(А)+Р(В)+…..P(K)

Если в урне 10 шаров, из них 3 черных, 7 белых. Какая вероятность появления или черного или белого шара? Конечно, вероятность появления или черного или белого шара равна 1, так как мы обязательно вытащим тот или другой шар.

P (Черный шар, Белый шар) = 3/10+7/10=1

В горизонтальной горной выработке – штольне через равный интервал были отобраны 35 проб. Содержание золота в пробах были определены в интервале от 1г/т до 10 г/т. Результаты опробования приводятся в таблице.

Содержание AU в пробе	Число проб
1	7
2	5
3	4
4	2
5	1
6	3
7	3
8	5
9	3
10	2

Какая вероятность появления в случайно взятой пробе содержания золота от 1 г/т до10 г/т и от 1 г/т до 5 г/т .

Если в этом опыте мы согласимся, что частота появления пробы с определенным содержанием золота равна вероятности, что будет из-за небольшого количества проб сильным допущением, то мы сможем найти ответы на поставленные вопросы. Конечно, ответ на первый вопрос прост. Вероятность взятия пробы с содержанием от 1 г/т до 10 г/т равна 1 или 100%. А вероятность появления события (В) – взятие пробы с содержанием золота от 1 г/т до 5 г/т равна Р, что прямо следует из анализа таблицы.

P=7/35+5/35+4/35+2/35+1/35=0.543

Таким образом -

P(B)=P(<5г/т)=0.543

Дата: 2018-12-28, просмотров: 286.

12 3 4 5 6 7 8 9 10 Следующая ⇒