Ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса.
Модуль и направление ускорения aM находятся построением соответствующего параллелограмма.
Однако вычисление аM с помощью параллелограмма, усложняет расчет, так как предварительно надо будет находить значение угла 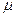 , а затем — угла между векторами aMA и aM. Поэтому при решении задач удобнее вектор aMA заменять его касательной (
, а затем — угла между векторами aMA и aM. Поэтому при решении задач удобнее вектор aMA заменять его касательной ( 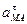 ) и нормальной (
) и нормальной ( 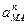 ) составляющими и представить равенство в виде:
) составляющими и представить равенство в виде:
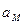 =
= 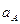 +
+ 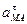 +
+ 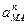 .
.
При этом вектор 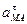 направлен перпендикулярно
направлен перпендикулярно 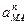 (рис.1.12) в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор
(рис.1.12) в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор 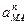 всегда направлен от точки М к полюсу . Численно же
всегда направлен от точки М к полюсу . Численно же 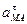 =АМ
=АМ 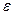 ,
, 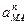 =AM
=AM 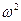 .
.
Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной и нормальной составляющих, тогда
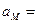
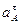 +
+ 
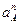 +
+ 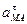 +
+ 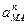
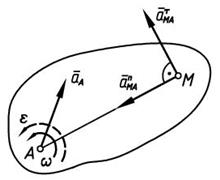
Рис.1.12
Для определения модуля ускорения точки 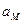 необходимо спроецировать последнее уравнение на координатные оси. В результате этого получим проекции ускорения точки М на указанные оси. Модуль ускорения точки М определяем по следующей формуле:
необходимо спроецировать последнее уравнение на координатные оси. В результате этого получим проекции ускорения точки М на указанные оси. Модуль ускорения точки М определяем по следующей формуле:
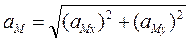
Задача 1
Для данного положения механизма определить ускорение ползуна В, если колесо 1 радиуса R =50см катится с постоянной скоростью его центра 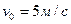 ; угол
; угол 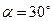 .
.
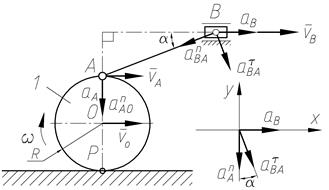
| Решение
Определим угловую скорость колеса. Так как тело катится без скольжения по неподвижной поверхности, то МЦС – Pv находится в точке контакта колеса с поверхностью и 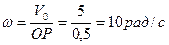
|
направлена по ходу часовой стрелки 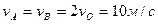 ,
, 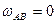 . Определим ускорение точки А. Приняв точку О за полюс
. Определим ускорение точки А. Приняв точку О за полюс 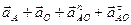 . Так как колесо катится с постоянной скоростью, то его угловое ускорение
. Так как колесо катится с постоянной скоростью, то его угловое ускорение 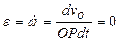 и касательное ускорение точки О равно нулю. Ускорение точки А равно.
и касательное ускорение точки О равно нулю. Ускорение точки А равно.
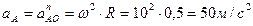
Ускорение точки В будет состоять из ускорения точки А плюс ускорения полученного от вращения точки В вокруг точки А.
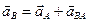
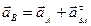
Так как скорости точек А и В параллельны между собой, то шатун АВ совершает мгновенно поступательное движение, а значит 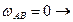
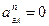
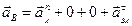 Спроецируем уравнение на оси x и y .
Спроецируем уравнение на оси x и y .
OX: 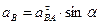
OY: 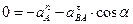
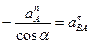
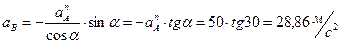
Ответ: 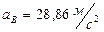
Сложное движение точки
Рассмотрим движение точки по отношению к двум системам отсчета, из которых одну считаем основной или условно неподвижной, а другую движущуюся по отношению к основной.
Движение, совершаемое точкой, называют сложным. Рассмотрим точку М, движущуюся по отношению к подвижной системе отсчета Оху z, которая в свою очередь движется относительно основной системы отсчета O0x0y0z0, (рис.1.13).
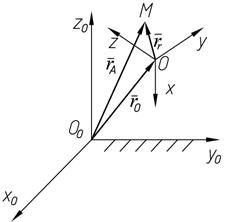
Рис.1.13
Движение, совершаемое точкой М по отношению к подвижной системе отсчета, называется относительным движением 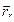 . Скорость называется относительной скоростью (
. Скорость называется относительной скоростью ( 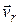 ), а ускорение – относительным ускорением (
), а ускорение – относительным ускорением ( 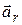 ).
).
Движение, совершаемое подвижной системой отсчета (и всеми связанными с нею точками) по отношению к неподвижной системе отсчета является для точки М переносным движением.
Скорость и ускорение точки, связанной с подвижными осями и с которой, в данный момент времени, совпадает движущаяся точка М, называют переносной скоростью ( 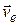 ), и переносным ускорением
), и переносным ускорением
точки М ( 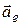 ).
).
Движение, совершаемое точкой по отношению к неподвижной системе, отсчета называется абсолютным 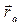 , его скорость и ускорение – абсолютной скоростью (
, его скорость и ускорение – абсолютной скоростью ( 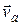 ) и - абсолютным ускорением (
) и - абсолютным ускорением ( 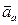 ).
).
Для решения задач кинематики необходимо установить зависимости между относительными, переносными и абсолютными скоростями и ускорениями точки.
1.15 Теорема сложения скоростей и ускорений – при
сложном движении точки
Абсолютная скорость точки равна векторной сумме ее относительной и переносной скоростей. 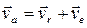
Модуль абсолютной скорости
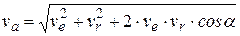 ,
,
где α – угол между векторами относительной и переносной скоростей точки.
При сложном движении точки ее абсолютное ускорение равно векторной сумме переносного, относительного и кориолисова ускорения
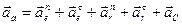 .
.
Задача 1
Определить абсолютную скорость в момент времени t =2 c точки М, которая движется по диагонали прямоугольной пластины 1 по закону M 0 M =0,3 t 2 . Сама пластина движется вертикально в плоскости рисунка согласно уравнению 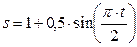 . Угол
. Угол 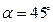 .
.
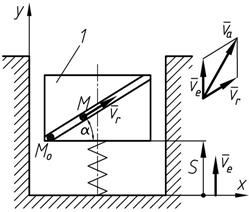
| Решение
Так как точка М совершает сложное движение, то ее скорость состоит из переносной 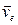 и относительной и относительной 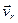 скоростей. скоростей.
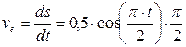
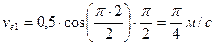
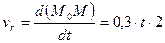
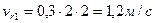
|
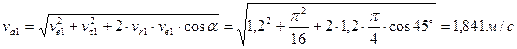
Ответ: 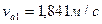
Ускорение Кориолиса
Ускорение Кориолиса характеризует быстроту изменения переносной скорости в относительном движении и изменение относительной скорости в переносном движении и равно
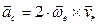 или
или 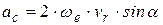 ,
,
где α – угол между векторами 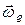 и
и 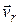 (рис. 2.15).
(рис. 2.15).
Из данной формулы видно, что Кориолисово ускорение может обращаться в нуль в следующих случаях:
1) ω e=0, т. е когда переносное движение является поступательным или переносная угловая скорость в данный момент времени обращается в нуль;
2) vr=0, т. е. когда относительная скорость в данный момент времени обращается в нуль;
3) когда α=0 (180º), т. е. когда относительное движение происходит по направлению, параллельному оси переносного вращения.
Направление вектора 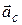 определяется по правилу Жуковского либо по правилу векторного произведения (рис.1.15):
определяется по правилу Жуковского либо по правилу векторного произведения (рис.1.15):
1. проецируем вектор относительной скорости 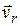 на плоскость, перпендикулярную оси переносного вращения;
на плоскость, перпендикулярную оси переносного вращения;
2. поворачиваем полученную проекцию на 90º по направлению переносного вращения (по направлению ω e) - это и есть направление кориолисова ускорения.
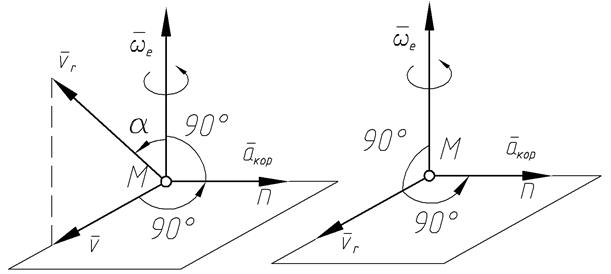
Рис.1.15
По правилу векторного произведения 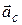 – вектор перпендикулярный
– вектор перпендикулярный 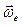 и
и 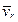 направлен так, чтобы поворот от
направлен так, чтобы поворот от 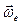 к
к 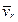 на угол
на угол 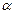 виден происходящим против хода часовой стрелки.
виден происходящим против хода часовой стрелки.
Задача 1
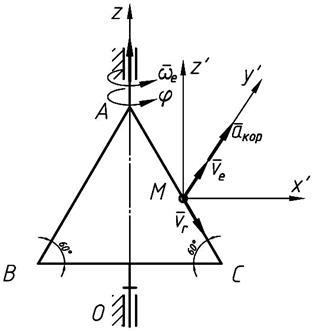
Пластина АВС вращается вокруг оси Oz по закону 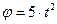 , а по ее стороне АС движется точка М согласно уравнения
, а по ее стороне АС движется точка М согласно уравнения 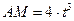 . Определить ускорение Кориолиса точки М в момент времени t 1 =0,5 c .
. Определить ускорение Кориолиса точки М в момент времени t 1 =0,5 c .
| Решение
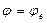 ; ; 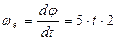
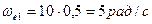
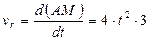 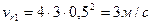 Кориолисово ускорение определяется по формуле:
Кориолисово ускорение определяется по формуле:
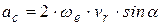 ,
где ,
где 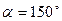 – угол между вектором угловой скорости – угол между вектором угловой скорости 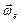 и вектором относительной скорости и вектором относительной скорости 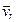 . .
|
Вращательное движение рамки является переносным движением, а движение точки по стороне АС – относительное движение.
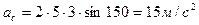 .
.
Ответ: 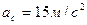
Дата: 2018-12-28, просмотров: 623.