Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости П (рис.1.5).
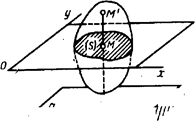
Рис.1.5
Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси. Прямая 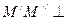 плоскости П движется поступательно и для изучения плоского движения достаточно рассмотреть движение плоской фигуры S.
плоскости П движется поступательно и для изучения плоского движения достаточно рассмотреть движение плоской фигуры S.
Положение плоской фигуры S в плоскости Оху определяется положением двух произвольных точек А и В этой фигуры (рис.1.6).
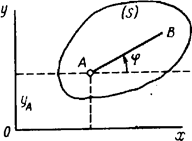
Рис.1.6
Положение отрезка АВ можно определить, зная координаты xA и yA точки А и угол φ, который отрезок АВ образует с осью Oх. Точку A, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
Для задания плоского движения тела достаточно задать положение полюса А – 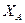 ,
, 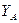 и угла φ
и угла φ
xA=f1(t); yA=f2(t); φ=f3(t).
Первые два уравнения определяют поступательное движение вместе с полюсом A. Третье уравнение определяет вращательное движение вокруг оси проходящей через полюс (ось Az).
Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения полюса:
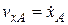 ;
; 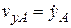 ;
; 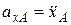 ;
; 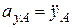 ,
,
а также угловая скорость и угловое ускорение вращательного движения вокруг полюса
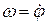 ;
; 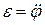 .
.
Определение скоростей точек плоской фигуры
Скорость произвольной точки М фигуры определим как сумма скоростей, которые точка получает при поступательном движении вместе с полюсом и вращательном движении вокруг полюса.
Представим положение точки М как 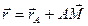 (рис.1.6).
(рис.1.6).
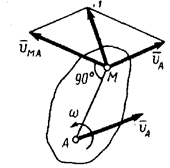
Рис.1.6
Продифференцировав это выражение по времени получим:
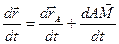 , т.к.
, т.к. 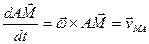
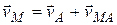 .
.
При этом скорость vMA. которую точка М получает при вращении фигуры вокруг полюса А, будет определяться из выражения
vMA=ω·MA,
где ω – угловая скорость плоской фигуры.
Скорость любой точки М плоской фигуры геометрически складывается из скорости точки А, принятой за полюс, и скорости, точки М при вращении фигуры вокруг полюса. Модуль и направление скорости этой скорости находятся построением параллелограмма скоростей.
Задача 1
Определить скорость точки А, если скорость центра катка равна 5м/с, угловая скорость катка 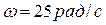 . Радиус катка r =0,2м, угол
. Радиус катка r =0,2м, угол 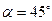 . Каток катится без скольжения.
. Каток катится без скольжения.
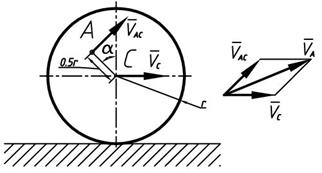
Решение
Так как тело совершает плоскопараллельное движение, то скорость точки А будет состоять из скорости полюса (точка С) и скорости полученной точкой А при вращении вокруг полюса С.
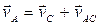 ,
,
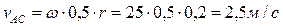
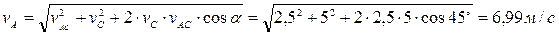
Ответ: 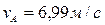
Дата: 2018-12-28, просмотров: 418.