ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 4
1.1 Векторный, координатный и естественный способы задания движения точки 5
1.2. Скорость и ускорения движущейся точки при векторном способе задания ее движения. 6
1.3. Скорость и ускорение точки при координатном способе задания ее движения 7
1.4. Скорость и ускорение точки при естественном способе задания движения 8
1.5. Поступательное движение твердого тела. 9
1.6. Вращательное движение твердого тела вокруг неподвижной оси 10
1.7. Скорость и ускорение точек тела при вращательном движении. 12
1.8. Плоскопараллельное движение твердого тела. 13
1.9. Определение скоростей точек плоской фигуры.. 14
1.10 Теорема о проекциях скоростей двух точек тела, движущего плоскопараллельно 16
1.11. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. 16
1.12. Некоторые частные случаи определения положения мгновенного центра скоростей. 18
1.13 Определение ускорения точек плоской фигуры.. 19
1.14. Сложное движение точки. 21
1.15 Теорема сложения скоростей и ускорений – при сложном движении точки 22
1.16 Ускорение Кориолиса. 23
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 25
ВВЕДЕНИЕ
Основной задачей настоящего методического указания является оказание помощи студенту заочной формы обучения при подготовке к аудиторной контрольной работе по разделу теоретической механики «Кинематика». При положительной оценке преподавателем результатов указанной контрольной работы студент будет допущен к сдаче зачета или экзамена по указанным разделам дисциплины «Теоретическая механика».
В контрольной работе содержатся два теоретических вопроса (один по разделу «Статика», второй по разделу «Кинематика») и одна задача на применение основных законов и принципов раздела «Статика» или «Кинематика».
В методических указаниях содержится минимум необходимый для ответов на теоретические вопросы материалов, а также примеры решения задач, тематика которых совпадает с тематикой задач, которые будут представлены при проведении аудиторной контрольной работы.
Рецензированию подлежат только те контрольные работы, в которых содержится ответ на один теоретический вопрос и дано решение предложенной задачи. Преподаватель оценивает полноту ответов на теоретические вопросы, правильность решения задачи и делает окончательное заключение о получении оценки «зачтено».
КИНЕМАТИКА
1.1 Векторный, координатный и естественный способы задания движения точки
Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Установление математических способов задания движения точек или тел является одной из важных задач кинематики.
Пусть точка М движется по отношению к некоторой системе отсчета Охуz (рис. 2.1).
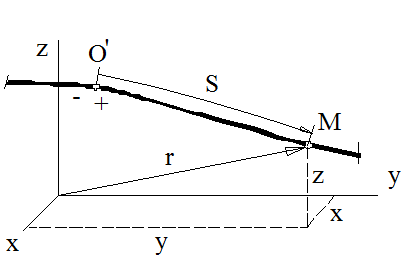
Рис.1.1
Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 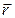 , проведенный из точки О в точку М.
, проведенный из точки О в точку М.
При движении точки М данный вектор будет с течением времени изменяться по величине, и по направлению. Следовательно, он является переменным вектором (вектором-функцией), зависящим от времени t:
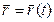 .
.
Это равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий радиус-вектор и найти положение движущейся точки в любой момент времени.
Если вместо зависимости 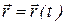 будут заданы координаты х, у и z точки как функции времени
будут заданы координаты х, у и z точки как функции времени
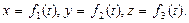 ,
,
то такой способ задания движения точки будет называться координатным.
Если движение точки происходит в одной плоскости, то, приняв эту плоскость за плоскость Оху, получим два уравнения движения:
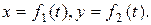
При прямолинейном движении точки, направив вдоль ее траектории координатную ось Ох, движение будет определяться одним уравнением
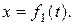
Естественным способом задания движения точки удобно пользоваться в случае, если известна траектория движущейся точки.
Движение точки считается описанным естественным способом, если известны (рис.2.1): траектория γ, дуговая координата 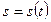 , начало отсчёта (O/), положительное (+) направление отсчета S. Величина s в уравнении определяет положение движущейся точки на траектории, а не пройденный ею путь.
, начало отсчёта (O/), положительное (+) направление отсчета S. Величина s в уравнении определяет положение движущейся точки на траектории, а не пройденный ею путь.
1.2. Скорость и ускорения движущейся точки при векторном способе задания ее движения
Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.
Скоростью точки называются вектор, определяющий быстроту и направления ее движения в каждый момент времени.
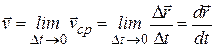 .
.
Вектор скорости точки равен первой производной от ее радиус-вектора по времени и направлен по касательной к траектории точки в сторону движения.
Размерность скорости 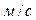 или
или 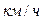 .
.
Ускорением точки называют вектор характеризующий быстроту изменения величины и направления скорости точки.
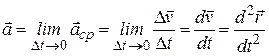 .
.
Вектор ускорения точки равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.
Размерность ускорения – [м/с2].
В общем случае вектор ускорения лежит в соприкасающейся плоскости и его можно разложить на нормальную и касательную составляющие 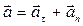 ;
; 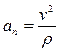 направлено по нормали к траектории точки в сторону вогнутости траектории.
направлено по нормали к траектории точки в сторону вогнутости траектории. 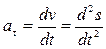 и направлено по касательной к траектории точки.
и направлено по касательной к траектории точки.
Положение точки на плоскости определяется ее радиус-вектором 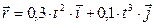 . Определить модуль ускорения точки в момент времени t 1 =2 c .
. Определить модуль ускорения точки в момент времени t 1 =2 c .
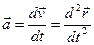 ;
; 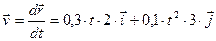 ;
;
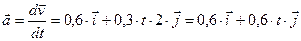 , т.к. вектора
, т.к. вектора 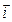 и
и 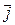 перпендикулярны между собой, то их сумму найдем по теореме Пифагора.
перпендикулярны между собой, то их сумму найдем по теореме Пифагора.
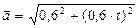 ;
; 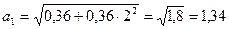 м/с2.
м/с2.
Ответ: 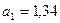 м/с2.
м/с2.
1.3. Скорость и ускорение точки при
координатном способе задания ее движения
Вектор скорости точки 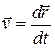 . Отсюда
. Отсюда 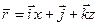
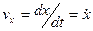 ;
; 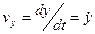 ;
; 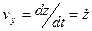
Проекции вектора скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции вектора скорости, найдем ее величину и направление.
Углы α, β и γ, которые вектор 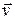 образует с координатными осями Ox, Oy, Oz соответственно, находятся как углы направляющих косинусов:
образует с координатными осями Ox, Oy, Oz соответственно, находятся как углы направляющих косинусов: 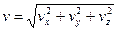 ;
; 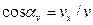 ;
; 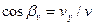 ;
; 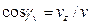 ,
,
Аналогично определяем координаты, направляющие косинусы и модуль ускорения:
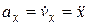 ;
; 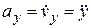 ;
; 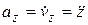 ;
;
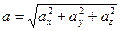 ;
; 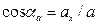 ;
; 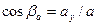 ;
; 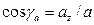 ;
;
Задача 1
Даны уравнения движения точки: 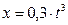 ,
, 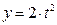 , где x и y – в см. Определить, в какой момент времени t 1 ускорение точки равно 7 см/с2.
, где x и y – в см. Определить, в какой момент времени t 1 ускорение точки равно 7 см/с2.
Решение
Полное ускорение точки состоит:
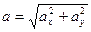
Ускорение точки определим через его проекции на оси координат Ох и О y 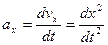 ;
; 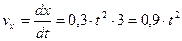 см/с;
см/с; 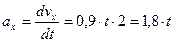 см/с2
см/с2
Ускорение 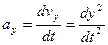 ;
; 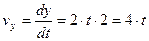 см/с;
см/с; 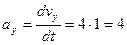 см/с2
см/с2
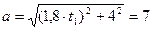 ;
;
Возведем обе части в квадрат и определим время t 1:
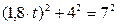
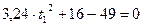 ;
; 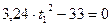 ;
; 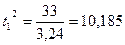 ;
; 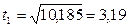 с.
с.
Ответ: 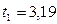 с
с
1.4. Скорость и ускорение точки при естественном
способе задания движения
Рассмотрим, определение скорости и ускорения точки при естественном способе задания движения, т.е. при задании траектории точки и закона движения точки вдоль этой траектории в виде s=f(t) (рис.1.2).
В этом случае значения векторов 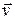 и
и 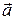 определяют по их проекциям на подвижные оси Мτ n b оси естественного трехгранника, с началом в движущейся точке М.
определяют по их проекциям на подвижные оси Мτ n b оси естественного трехгранника, с началом в движущейся точке М.
Ось Mτ – направлена по касательной к траектории точки в сторону положительного отсчета координаты s; ось Мп – по главной нормали к траектории точки. Ось Mb – перпендикулярно к первым двум так, чтобы оси образовывали правую систему координат. Mτ – касательная,
Мп – нормальная и Mb – бинормальная оси координат.
Величина скорости точки равна первой производной дуговой координаты точки S по времени:
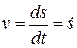 .
.
Скорость точки v направлена в сторону положительного отсчета s, когда v > 0 при v < 0 в противоположную сторону.
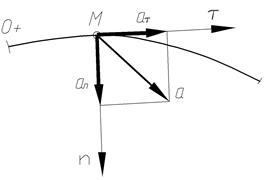
Рис.1.2
Вектор ускорения точки определяется его касательной 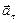 и нормальной
и нормальной 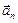 составляющими.
составляющими.
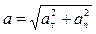 ,
,
Которые равны: 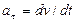 ;
; 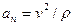 ,
,
где 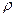 – радиус кривизны траектории в точке М.
– радиус кривизны траектории в точке М.
При 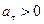 вектор
вектор 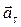 совпадает с направлением оси Мτ, а при
совпадает с направлением оси Мτ, а при 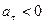 – в противоположную сторону.
– в противоположную сторону.
an – всегда положительно направлено по главной нормали.
Задача 1
Задано уравнение движения по криволинейной траектории: 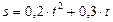 Определить полное ускорение точки в момент времени
Определить полное ускорение точки в момент времени 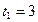 с, если в этот момент радиус кривизны траектории
с, если в этот момент радиус кривизны траектории 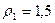 м.
м.
Так как точка движется по криволинейной траектории, то ускорение имеет две составляющие aτ – касательное; an – нормальное и 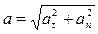 .
.
Составляющие полного ускорения равны:
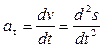 ;
; 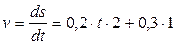 при t 1 =3 c
при t 1 =3 c
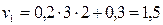 м/с;
м/с;
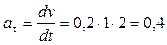 м/с2= const;
м/с2= const;
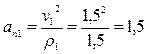 м/с2;
м/с2;
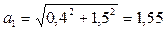 м/с2.
м/с2.
Точка совершает криволинейное равноускоренное движение.
Ответ: 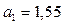 м/с2.
м/с2.
Задача 1
При вращении кривошипа ОА=О1В=0,16м угол 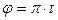 . Определить скорость и ускорение точки D полукруга ABD при t 1 =2с, если АВ=0,25м.
. Определить скорость и ускорение точки D полукруга ABD при t 1 =2с, если АВ=0,25м.
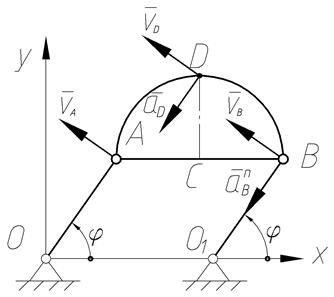
| Решение 1. Определим направление вектора скорости точки А; В и D. Так как точки А; В и D совершают движение по окружности, скорости этих точек будут направлены по касательной к окружности радиуса R =0,16м и параллельны друг другу. Если скорости точек тела равны между собой, то тело совершает поступательное движение. |
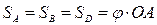 ;
;
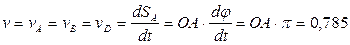 м/с = const
м/с = const
Так как полукруг ABD совершает поступательное движение, то ускорение точки D будет равно ускорению любой другой его точки. Так как точка В совершает криволинейное движение, то имеет две составляющие ускорения aτ – касательное; an – нормальное.
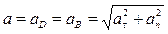
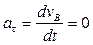
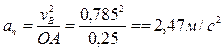
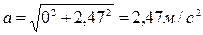
Ответ: 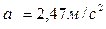
Задача 1
Тело вращается вокруг неподвижной оси согласно закону 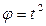 . Определить угловую скорость
. Определить угловую скорость 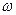 и угловое ускорение
и угловое ускорение 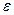 данного тела в момент времени, когда тело повернулось на угол
данного тела в момент времени, когда тело повернулось на угол 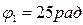 .
.
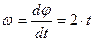
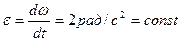
Определим момент времени t
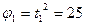
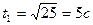
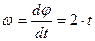
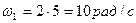
Ответ: 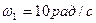 ,
, 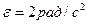
Задача 1
Угол поворота тела изменяется по закону 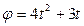 . Определить полное ускорение точки тела на расстоянии r=0,25м от оси вращения, в момент времени t1=3c.
. Определить полное ускорение точки тела на расстоянии r=0,25м от оси вращения, в момент времени t1=3c.
Решение
Так как точка движется по окружности, то ее ускорение можно разложить на составляющие aτ – касательное; an – нормальное.
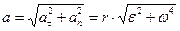
Определим угловую скорость и угловое ускорение точки:
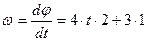
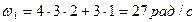
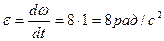
При t 1 =3 c: 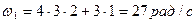
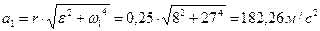
Ответ: 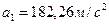
Задача 1
Определить скорость точки А, если скорость центра катка равна 5м/с, угловая скорость катка 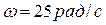 . Радиус катка r =0,2м, угол
. Радиус катка r =0,2м, угол 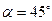 . Каток катится без скольжения.
. Каток катится без скольжения.
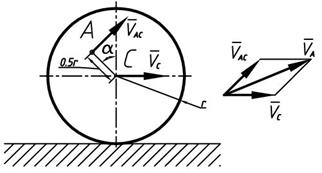
Решение
Так как тело совершает плоскопараллельное движение, то скорость точки А будет состоять из скорости полюса (точка С) и скорости полученной точкой А при вращении вокруг полюса С.
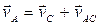 ,
,
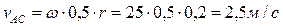
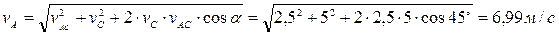
Ответ: 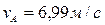
Задача 1
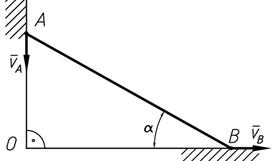
Стержень АВ скользит по гладкой стене вниз и гладкому полу, скорость точки A VA =5м/с, угол между полом и стержнем АВ равен 300. Определить скорость точки В.
 Ответ:
Ответ: 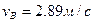
| Решение
Так как точки А и В принадлежат одному телу, то воспользуемся теоремой о проекции скоростей двух точек тела на прямую проходящую через эти точки.
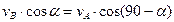
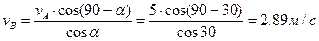
|
Задача 1
Кривошип ОА длиной 0,2м вращается равномерно с угловой скоростью ω =8 рад/с. К шатуну АВ в точке С шарнирно прикреплен шатун CD . Для заданного положения механизма определить скорость точки D ползуна, если угол 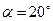 .
.
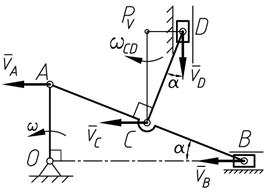
| Решение
Так как точка А принадлежит кривошипу ОА совершающему вращательное движение вокруг точки О, то скорость этой точки равна 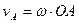 и направлена и направлена 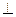 к ОА в сторону к ОА в сторону 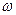 . .
|
Движение точки В ограничено горизонтальными направляющими, ползун может совершать только поступательное движение по горизонтальным направляющим. Скорость точки В 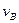 направлена в туже сторону что и
направлена в туже сторону что и 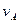 . Так как две точки шатуна имеют одинаковое направление
. Так как две точки шатуна имеют одинаковое направление 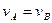 скоростей, то тело совершает мгновенно поступательное движение, и скорости всех точек шатуна имеют одинаковое направление и значение.
скоростей, то тело совершает мгновенно поступательное движение, и скорости всех точек шатуна имеют одинаковое направление и значение.
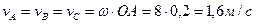
Шатун CD совершает плоскопараллельное движение. Мгновенный центр скоростей шатуна С D – P лежит на пересечении перпендикуляров к 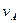 и
и 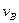 . Определим угловую скорость шатуна CD и скорость точки D.
. Определим угловую скорость шатуна CD и скорость точки D.
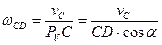
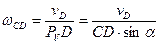
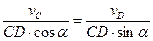
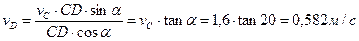
Ответ: 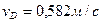
1.12. Некоторые частные случаи определения положения мгновенного центра скоростей
Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого - неподвижного, то точка Р касания этих тел, является мгновенным центром скоростей рис.1.9.
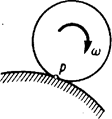
Рис.1.9
Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна скоростям этих точек, то мгновенный центр скоростей Р лежит на пересечении прямых соединяющих начало и концы векторов 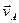 и
и 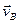 рис.1.10, а, б.
рис.1.10, а, б.
Угловая скорость тела равна: 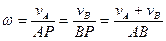
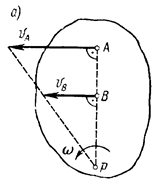
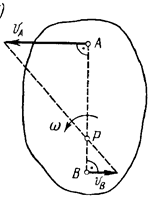
Рис.1.10
Если скорости точек А и В плоской фигуры параллельны и одинаково направлены, причем отрезок AB не перпендикулярен данным скоростям, то мгновенный центр скоростей лежит в бесконечности и скорости всех точек тела равны (рис.1.11). Угловая скорость тела ω в этот момент времени равна нулю. Тело совершает мгновенно поступательное движение.
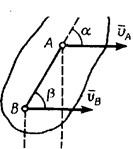
Рис.1.11
Задача 1
Для данного положения механизма определить ускорение ползуна В, если колесо 1 радиуса R =50см катится с постоянной скоростью его центра 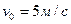 ; угол
; угол 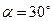 .
.
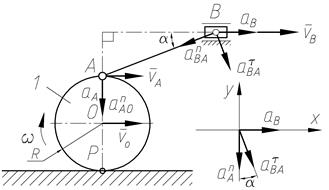
| Решение
Определим угловую скорость колеса. Так как тело катится без скольжения по неподвижной поверхности, то МЦС – Pv находится в точке контакта колеса с поверхностью и 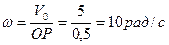
|
направлена по ходу часовой стрелки 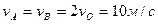 ,
, 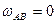 . Определим ускорение точки А. Приняв точку О за полюс
. Определим ускорение точки А. Приняв точку О за полюс 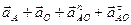 . Так как колесо катится с постоянной скоростью, то его угловое ускорение
. Так как колесо катится с постоянной скоростью, то его угловое ускорение 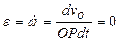 и касательное ускорение точки О равно нулю. Ускорение точки А равно.
и касательное ускорение точки О равно нулю. Ускорение точки А равно.
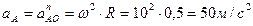
Ускорение точки В будет состоять из ускорения точки А плюс ускорения полученного от вращения точки В вокруг точки А.
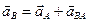
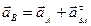
Так как скорости точек А и В параллельны между собой, то шатун АВ совершает мгновенно поступательное движение, а значит 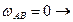
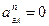
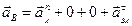 Спроецируем уравнение на оси x и y .
Спроецируем уравнение на оси x и y .
OX: 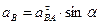
OY: 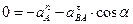
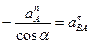
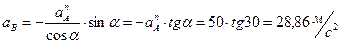
Ответ: 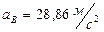
Сложное движение точки
Рассмотрим движение точки по отношению к двум системам отсчета, из которых одну считаем основной или условно неподвижной, а другую движущуюся по отношению к основной.
Движение, совершаемое точкой, называют сложным. Рассмотрим точку М, движущуюся по отношению к подвижной системе отсчета Оху z, которая в свою очередь движется относительно основной системы отсчета O0x0y0z0, (рис.1.13).
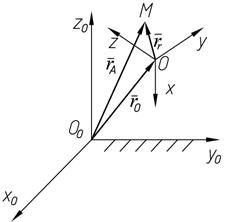
Рис.1.13
Движение, совершаемое точкой М по отношению к подвижной системе отсчета, называется относительным движением 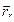 . Скорость называется относительной скоростью (
. Скорость называется относительной скоростью ( 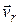 ), а ускорение – относительным ускорением (
), а ускорение – относительным ускорением ( 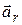 ).
).
Движение, совершаемое подвижной системой отсчета (и всеми связанными с нею точками) по отношению к неподвижной системе отсчета является для точки М переносным движением.
Скорость и ускорение точки, связанной с подвижными осями и с которой, в данный момент времени, совпадает движущаяся точка М, называют переносной скоростью ( 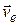 ), и переносным ускорением
), и переносным ускорением
точки М ( 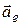 ).
).
Движение, совершаемое точкой по отношению к неподвижной системе, отсчета называется абсолютным 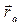 , его скорость и ускорение – абсолютной скоростью (
, его скорость и ускорение – абсолютной скоростью ( 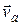 ) и - абсолютным ускорением (
) и - абсолютным ускорением ( 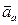 ).
).
Для решения задач кинематики необходимо установить зависимости между относительными, переносными и абсолютными скоростями и ускорениями точки.
1.15 Теорема сложения скоростей и ускорений – при
сложном движении точки
Абсолютная скорость точки равна векторной сумме ее относительной и переносной скоростей. 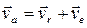
Модуль абсолютной скорости
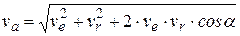 ,
,
где α – угол между векторами относительной и переносной скоростей точки.
При сложном движении точки ее абсолютное ускорение равно векторной сумме переносного, относительного и кориолисова ускорения
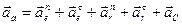 .
.
Задача 1
Определить абсолютную скорость в момент времени t =2 c точки М, которая движется по диагонали прямоугольной пластины 1 по закону M 0 M =0,3 t 2 . Сама пластина движется вертикально в плоскости рисунка согласно уравнению 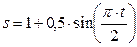 . Угол
. Угол 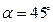 .
.
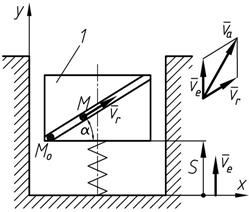
| Решение
Так как точка М совершает сложное движение, то ее скорость состоит из переносной 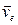 и относительной и относительной 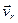 скоростей. скоростей.
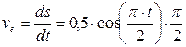
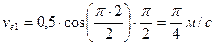
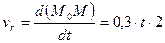
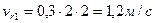
|
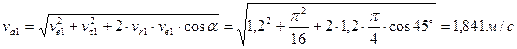
Ответ: 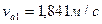
Ускорение Кориолиса
Ускорение Кориолиса характеризует быстроту изменения переносной скорости в относительном движении и изменение относительной скорости в переносном движении и равно
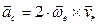 или
или 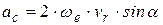 ,
,
где α – угол между векторами 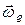 и
и 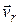 (рис. 2.15).
(рис. 2.15).
Из данной формулы видно, что Кориолисово ускорение может обращаться в нуль в следующих случаях:
1) ω e=0, т. е когда переносное движение является поступательным или переносная угловая скорость в данный момент времени обращается в нуль;
2) vr=0, т. е. когда относительная скорость в данный момент времени обращается в нуль;
3) когда α=0 (180º), т. е. когда относительное движение происходит по направлению, параллельному оси переносного вращения.
Направление вектора 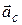 определяется по правилу Жуковского либо по правилу векторного произведения (рис.1.15):
определяется по правилу Жуковского либо по правилу векторного произведения (рис.1.15):
1. проецируем вектор относительной скорости 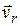 на плоскость, перпендикулярную оси переносного вращения;
на плоскость, перпендикулярную оси переносного вращения;
2. поворачиваем полученную проекцию на 90º по направлению переносного вращения (по направлению ω e) - это и есть направление кориолисова ускорения.
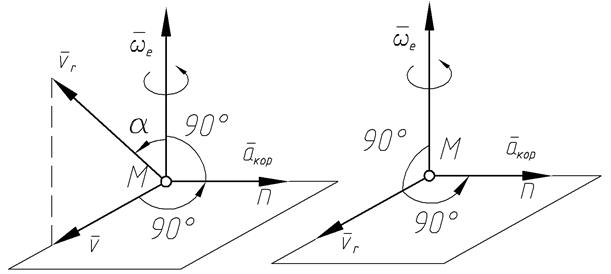
Рис.1.15
По правилу векторного произведения 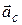 – вектор перпендикулярный
– вектор перпендикулярный 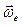 и
и 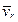 направлен так, чтобы поворот от
направлен так, чтобы поворот от 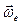 к
к 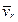 на угол
на угол 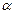 виден происходящим против хода часовой стрелки.
виден происходящим против хода часовой стрелки.
Задача 1
Пластина АВС вращается вокруг оси Oz по закону 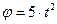 , а по ее стороне АС движется точка М согласно уравнения
, а по ее стороне АС движется точка М согласно уравнения 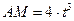 . Определить ускорение Кориолиса точки М в момент времени t 1 =0,5 c .
. Определить ускорение Кориолиса точки М в момент времени t 1 =0,5 c .
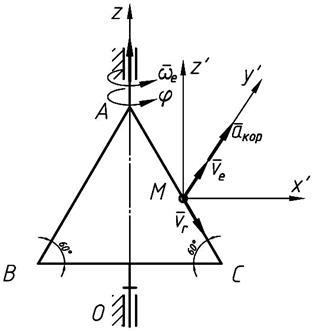
| Решение
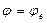 ; ; 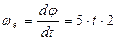
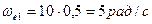
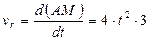 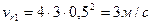 Кориолисово ускорение определяется по формуле:
Кориолисово ускорение определяется по формуле:
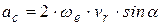 ,
где ,
где 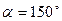 – угол между вектором угловой скорости – угол между вектором угловой скорости 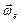 и вектором относительной скорости и вектором относительной скорости 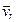 . .
|
Вращательное движение рамки является переносным движением, а движение точки по стороне АС – относительное движение.
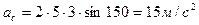 .
.
Ответ: 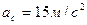
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ. 4
1.1 Векторный, координатный и естественный способы задания движения точки 5
1.2. Скорость и ускорения движущейся точки при векторном способе задания ее движения. 6
1.3. Скорость и ускорение точки при координатном способе задания ее движения 7
1.4. Скорость и ускорение точки при естественном способе задания движения 8
1.5. Поступательное движение твердого тела. 9
1.6. Вращательное движение твердого тела вокруг неподвижной оси 10
1.7. Скорость и ускорение точек тела при вращательном движении. 12
1.8. Плоскопараллельное движение твердого тела. 13
1.9. Определение скоростей точек плоской фигуры.. 14
1.10 Теорема о проекциях скоростей двух точек тела, движущего плоскопараллельно 16
1.11. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. 16
1.12. Некоторые частные случаи определения положения мгновенного центра скоростей. 18
1.13 Определение ускорения точек плоской фигуры.. 19
1.14. Сложное движение точки. 21
1.15 Теорема сложения скоростей и ускорений – при сложном движении точки 22
1.16 Ускорение Кориолиса. 23
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 25
ВВЕДЕНИЕ
Основной задачей настоящего методического указания является оказание помощи студенту заочной формы обучения при подготовке к аудиторной контрольной работе по разделу теоретической механики «Кинематика». При положительной оценке преподавателем результатов указанной контрольной работы студент будет допущен к сдаче зачета или экзамена по указанным разделам дисциплины «Теоретическая механика».
В контрольной работе содержатся два теоретических вопроса (один по разделу «Статика», второй по разделу «Кинематика») и одна задача на применение основных законов и принципов раздела «Статика» или «Кинематика».
В методических указаниях содержится минимум необходимый для ответов на теоретические вопросы материалов, а также примеры решения задач, тематика которых совпадает с тематикой задач, которые будут представлены при проведении аудиторной контрольной работы.
Рецензированию подлежат только те контрольные работы, в которых содержится ответ на один теоретический вопрос и дано решение предложенной задачи. Преподаватель оценивает полноту ответов на теоретические вопросы, правильность решения задачи и делает окончательное заключение о получении оценки «зачтено».
КИНЕМАТИКА
1.1 Векторный, координатный и естественный способы задания движения точки
Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.
Установление математических способов задания движения точек или тел является одной из важных задач кинематики.
Пусть точка М движется по отношению к некоторой системе отсчета Охуz (рис. 2.1).

Рис.1.1
Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 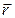 , проведенный из точки О в точку М.
, проведенный из точки О в точку М.
При движении точки М данный вектор будет с течением времени изменяться по величине, и по направлению. Следовательно, он является переменным вектором (вектором-функцией), зависящим от времени t:
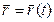 .
.
Это равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий радиус-вектор и найти положение движущейся точки в любой момент времени.
Если вместо зависимости 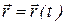 будут заданы координаты х, у и z точки как функции времени
будут заданы координаты х, у и z точки как функции времени
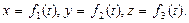 ,
,
то такой способ задания движения точки будет называться координатным.
Если движение точки происходит в одной плоскости, то, приняв эту плоскость за плоскость Оху, получим два уравнения движения:
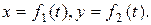
При прямолинейном движении точки, направив вдоль ее траектории координатную ось Ох, движение будет определяться одним уравнением
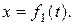
Естественным способом задания движения точки удобно пользоваться в случае, если известна траектория движущейся точки.
Движение точки считается описанным естественным способом, если известны (рис.2.1): траектория γ, дуговая координата 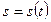 , начало отсчёта (O/), положительное (+) направление отсчета S. Величина s в уравнении определяет положение движущейся точки на траектории, а не пройденный ею путь.
, начало отсчёта (O/), положительное (+) направление отсчета S. Величина s в уравнении определяет положение движущейся точки на траектории, а не пройденный ею путь.
1.2. Скорость и ускорения движущейся точки при векторном способе задания ее движения
Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение.
Скоростью точки называются вектор, определяющий быстроту и направления ее движения в каждый момент времени.
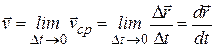 .
.
Вектор скорости точки равен первой производной от ее радиус-вектора по времени и направлен по касательной к траектории точки в сторону движения.
Размерность скорости 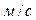 или
или 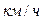 .
.
Ускорением точки называют вектор характеризующий быстроту изменения величины и направления скорости точки.
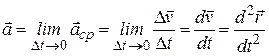 .
.
Вектор ускорения точки равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.
Размерность ускорения – [м/с2].
В общем случае вектор ускорения лежит в соприкасающейся плоскости и его можно разложить на нормальную и касательную составляющие 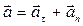 ;
; 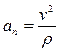 направлено по нормали к траектории точки в сторону вогнутости траектории.
направлено по нормали к траектории точки в сторону вогнутости траектории. 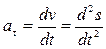 и направлено по касательной к траектории точки.
и направлено по касательной к траектории точки.
Положение точки на плоскости определяется ее радиус-вектором 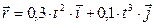 . Определить модуль ускорения точки в момент времени t 1 =2 c .
. Определить модуль ускорения точки в момент времени t 1 =2 c .
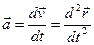 ;
; 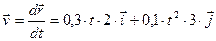 ;
;
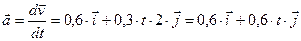 , т.к. вектора
, т.к. вектора 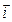 и
и 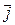 перпендикулярны между собой, то их сумму найдем по теореме Пифагора.
перпендикулярны между собой, то их сумму найдем по теореме Пифагора.
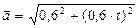 ;
; 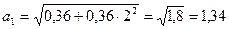 м/с2.
м/с2.
Ответ: 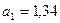 м/с2.
м/с2.
1.3. Скорость и ускорение точки при
координатном способе задания ее движения
Вектор скорости точки 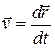 . Отсюда
. Отсюда 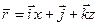
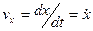 ;
; 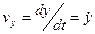 ;
; 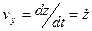
Проекции вектора скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции вектора скорости, найдем ее величину и направление.
Углы α, β и γ, которые вектор 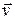 образует с координатными осями Ox, Oy, Oz соответственно, находятся как углы направляющих косинусов:
образует с координатными осями Ox, Oy, Oz соответственно, находятся как углы направляющих косинусов: 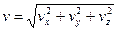 ;
; 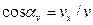 ;
; 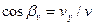 ;
; 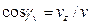 ,
,
Аналогично определяем координаты, направляющие косинусы и модуль ускорения:
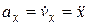 ;
; 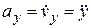 ;
; 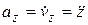 ;
;
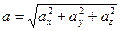 ;
; 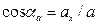 ;
; 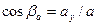 ;
; 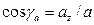 ;
;
Задача 1
Даны уравнения движения точки: 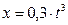 ,
, 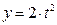 , где x и y – в см. Определить, в какой момент времени t 1 ускорение точки равно 7 см/с2.
, где x и y – в см. Определить, в какой момент времени t 1 ускорение точки равно 7 см/с2.
Решение
Полное ускорение точки состоит:
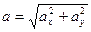
Ускорение точки определим через его проекции на оси координат Ох и О y 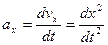 ;
; 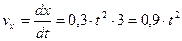 см/с;
см/с; 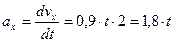 см/с2
см/с2
Ускорение 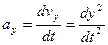 ;
; 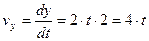 см/с;
см/с; 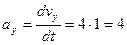 см/с2
см/с2
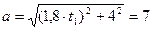 ;
;
Возведем обе части в квадрат и определим время t 1:
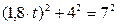
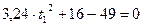 ;
; 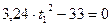 ;
; 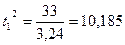 ;
; 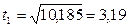 с.
с.
Ответ: 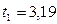 с
с
1.4. Скорость и ускорение точки при естественном
способе задания движения
Рассмотрим, определение скорости и ускорения точки при естественном способе задания движения, т.е. при задании траектории точки и закона движения точки вдоль этой траектории в виде s=f(t) (рис.1.2).
В этом случае значения векторов 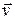 и
и 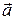 определяют по их проекциям на подвижные оси Мτ n b оси естественного трехгранника, с началом в движущейся точке М.
определяют по их проекциям на подвижные оси Мτ n b оси естественного трехгранника, с началом в движущейся точке М.
Ось Mτ – направлена по касательной к траектории точки в сторону положительного отсчета координаты s; ось Мп – по главной нормали к траектории точки. Ось Mb – перпендикулярно к первым двум так, чтобы оси образовывали правую систему координат. Mτ – касательная,
Мп – нормальная и Mb – бинормальная оси координат.
Величина скорости точки равна первой производной дуговой координаты точки S по времени:
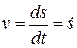 .
.
Скорость точки v направлена в сторону положительного отсчета s, когда v > 0 при v < 0 в противоположную сторону.

Рис.1.2
Вектор ускорения точки определяется его касательной 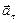 и нормальной
и нормальной 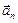 составляющими.
составляющими.
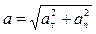 ,
,
Которые равны: 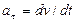 ;
; 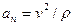 ,
,
где 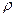 – радиус кривизны траектории в точке М.
– радиус кривизны траектории в точке М.
При 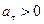 вектор
вектор 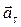 совпадает с направлением оси Мτ, а при
совпадает с направлением оси Мτ, а при 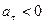 – в противоположную сторону.
– в противоположную сторону.
an – всегда положительно направлено по главной нормали.
Задача 1
Задано уравнение движения по криволинейной траектории: 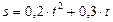 Определить полное ускорение точки в момент времени
Определить полное ускорение точки в момент времени 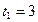 с, если в этот момент радиус кривизны траектории
с, если в этот момент радиус кривизны траектории 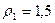 м.
м.
Так как точка движется по криволинейной траектории, то ускорение имеет две составляющие aτ – касательное; an – нормальное и 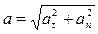 .
.
Составляющие полного ускорения равны:
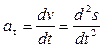 ;
; 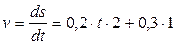 при t 1 =3 c
при t 1 =3 c
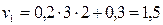 м/с;
м/с;
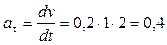 м/с2= const;
м/с2= const;
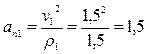 м/с2;
м/с2;
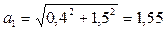 м/с2.
м/с2.
Точка совершает криволинейное равноускоренное движение.
Ответ: 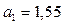 м/с2.
м/с2.
Поступательное движение твердого тела
Поступательным движением твердого тела называют такое его движение, при котором любая прямая, проведенная на этом теле, перемещается, оставаясь параллельной своему начальному направлению: 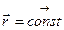
При поступательном движении тела траектории его точек могут быть любыми линиями (прямолинейными, плоскими и пространственными).
Поступательное движение тела определяется следующей теоремой: при поступательном движении все точки тела описывают геометрически одинаковые траектории и имеют в каждый момент времени одинаковые скорости и ускорения.
Из теоремы следует, что поступательное движение твердого тела вполне определяется движением одной его точки. Следовательно, изучение поступательного движения тела сводится к кинематике точки. 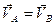 ;
; 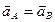
При поступательном движении общую для всех точек тела скорость 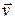 называют скоростью поступательного движения тела, а ускорение
называют скоростью поступательного движения тела, а ускорение
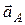 – ускорением поступательного движения тела. Эти векторы можно изображать к любой точке тела.
– ускорением поступательного движения тела. Эти векторы можно изображать к любой точке тела.
Понятия о скорости и ускорении твердого тела имеют смысл только при поступательном его движении.
Задача 1
При вращении кривошипа ОА=О1В=0,16м угол 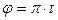 . Определить скорость и ускорение точки D полукруга ABD при t 1 =2с, если АВ=0,25м.
. Определить скорость и ускорение точки D полукруга ABD при t 1 =2с, если АВ=0,25м.

| Решение 1. Определим направление вектора скорости точки А; В и D. Так как точки А; В и D совершают движение по окружности, скорости этих точек будут направлены по касательной к окружности радиуса R =0,16м и параллельны друг другу. Если скорости точек тела равны между собой, то тело совершает поступательное движение. |
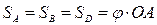 ;
;
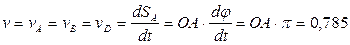 м/с = const
м/с = const
Так как полукруг ABD совершает поступательное движение, то ускорение точки D будет равно ускорению любой другой его точки. Так как точка В совершает криволинейное движение, то имеет две составляющие ускорения aτ – касательное; an – нормальное.
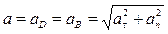
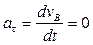
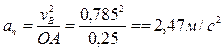
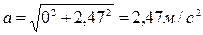
Ответ: 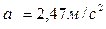
Дата: 2018-12-28, просмотров: 544.