Рассмотрим две точки А и В плоской фигуры. Принимая точку А за полюс (рис.1.7), получаем
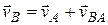 .
.
Отсюда, проецируя обе части равенства на АВ, и учитывая, что вектор 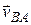 перпендикулярен АВ, находим
перпендикулярен АВ, находим
vB·cos β=vA·cos α + v В A·cos90°.
т.к. v В A·cos 90°=0 получаем: проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны.
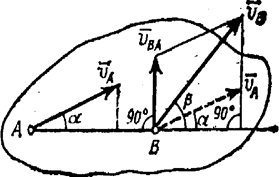
Рис.1.7
Задача 1
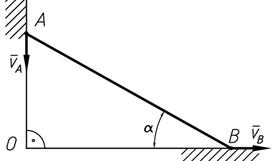
Стержень АВ скользит по гладкой стене вниз и гладкому полу, скорость точки A VA =5м/с, угол между полом и стержнем АВ равен 300. Определить скорость точки В.
 Ответ:
Ответ: 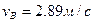
| Решение
Так как точки А и В принадлежат одному телу, то воспользуемся теоремой о проекции скоростей двух точек тела на прямую проходящую через эти точки.
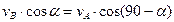
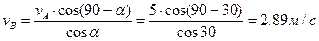
|
Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей
При определении скоростей точек плоской фигуры через скорость полюса, скорость полюса и скорость вращательного движения вокруг полюса могут быть равны по величине и противоположны по направлению и существует такая точка Р, скорость которой в данный момент времени равна нулю 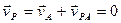 .
.
Мгновенным центром скоростей называется точка, связанная с плоской фигурой, скорость которой в данный момент времени равна нулю.
Скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было мгновенно вращательным вокруг оси проходящей через мгновенный центр скоростей (рис. 1.8).
vA=ω·PA; ( 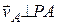 ).
).
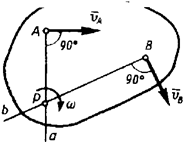
Рис.1.8
Т.к. vB=ω·PB; ( 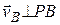 ), то w = vB/PB=vA/PA
), то w = vB/PB=vA/PA
Скорости точек плоской фигуры пропорциональны кратчайшим расстояниям от этих точек до мгновенного центра скоростей.
Полученные результаты приводят к следующим выводам:
1) для определения положения мгновенного центра скоростей надо знать величину и направления скорости 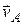 и направление скорости
и направление скорости 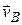 каких-нибудь двух точек А и В плоской фигуры; мгновенный центр скоростей P находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек;
каких-нибудь двух точек А и В плоской фигуры; мгновенный центр скоростей P находится в точке пересечения перпендикуляров, восставленных из точек А и В к скоростям этих точек;
2) угловая скорость ω плоской фигуры в данный момент времени равна отношению скорости 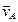 к расстоянию от нее до мгновенного центра Р скоростей: ω=v А/PА;
к расстоянию от нее до мгновенного центра Р скоростей: ω=v А/PА;
3) Скорость точки 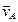 по отношению к мгновенному центру скоростей P укажет направление угловой скорости w.
по отношению к мгновенному центру скоростей P укажет направление угловой скорости w.
4) Величина скорости точки 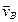 прямопропорциональна кратчайшему расстоянию от точки В к мгновенному центру скоростей Р vА = ω·ВР
прямопропорциональна кратчайшему расстоянию от точки В к мгновенному центру скоростей Р vА = ω·ВР
Задача 1
Кривошип ОА длиной 0,2м вращается равномерно с угловой скоростью ω =8 рад/с. К шатуну АВ в точке С шарнирно прикреплен шатун CD . Для заданного положения механизма определить скорость точки D ползуна, если угол 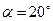 .
.
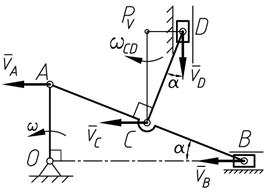
| Решение
Так как точка А принадлежит кривошипу ОА совершающему вращательное движение вокруг точки О, то скорость этой точки равна 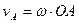 и направлена и направлена 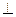 к ОА в сторону к ОА в сторону 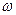 . .
|
Движение точки В ограничено горизонтальными направляющими, ползун может совершать только поступательное движение по горизонтальным направляющим. Скорость точки В 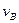 направлена в туже сторону что и
направлена в туже сторону что и 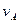 . Так как две точки шатуна имеют одинаковое направление
. Так как две точки шатуна имеют одинаковое направление 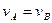 скоростей, то тело совершает мгновенно поступательное движение, и скорости всех точек шатуна имеют одинаковое направление и значение.
скоростей, то тело совершает мгновенно поступательное движение, и скорости всех точек шатуна имеют одинаковое направление и значение.
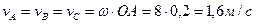
Шатун CD совершает плоскопараллельное движение. Мгновенный центр скоростей шатуна С D – P лежит на пересечении перпендикуляров к 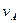 и
и 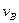 . Определим угловую скорость шатуна CD и скорость точки D.
. Определим угловую скорость шатуна CD и скорость точки D.
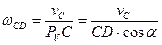
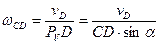
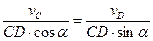
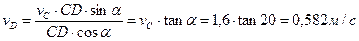
Ответ: 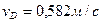
1.12. Некоторые частные случаи определения положения мгновенного центра скоростей
Если плоскопараллельное движение осуществляется путем качения без скольжения одного цилиндрического тела по поверхности другого - неподвижного, то точка Р касания этих тел, является мгновенным центром скоростей рис.1.9.
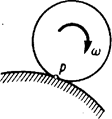
Рис.1.9
Если скорости точек А и В плоской фигуры параллельны друг другу и при этом линия АВ перпендикулярна скоростям этих точек, то мгновенный центр скоростей Р лежит на пересечении прямых соединяющих начало и концы векторов 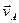 и
и 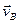 рис.1.10, а, б.
рис.1.10, а, б.
Угловая скорость тела равна: 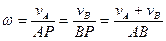
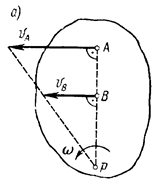
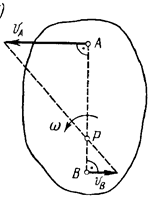
Рис.1.10
Если скорости точек А и В плоской фигуры параллельны и одинаково направлены, причем отрезок AB не перпендикулярен данным скоростям, то мгновенный центр скоростей лежит в бесконечности и скорости всех точек тела равны (рис.1.11). Угловая скорость тела ω в этот момент времени равна нулю. Тело совершает мгновенно поступательное движение.
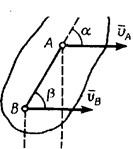
Рис.1.11
Дата: 2018-12-28, просмотров: 529.