Если каждую обмотку трехфазного генератора соединить со своим приемником, образуются три независимых цепи, каждая со своим током. (Рис.5.12).
Одна такая цепь и ее элементы называется фазой. В несвязанной трехфазной системе генератор соединяется с приемником энергии шестью проводами.
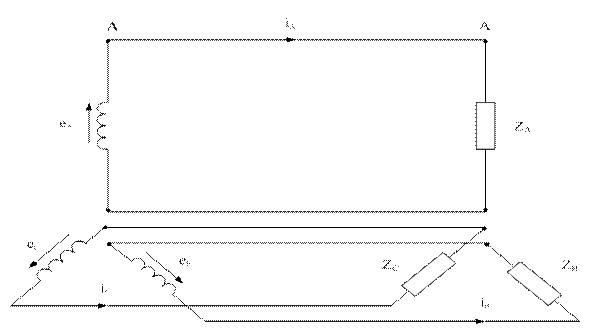
Рисунок 5.12
Недостатком такой цепи является большое число соединительных проводов. Сокращение числа соединительных проводов достигается, когда обмотки генератора и фазы приемника соединяются звездой (рис. 5.13 а) или треугольником (рис. 5.13 б).
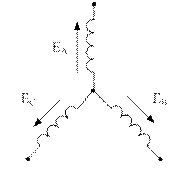
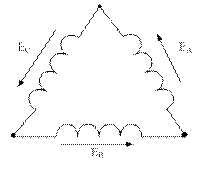
а) б)
Рисунок 5.13
5.3. Соединение звездой при симметричной нагрузке.
На рисунке 5.14 показана связанная система при соединении фаз источника энергии и приемника звездой. Такая система легко может быть получена из шестипроводной. Провода соединяющие начала А, В и С обмоток источника с приемником (линейные провода), сохраняются, а три провода, присоединенные к концам обмоток, заменяются одним. Благодаря этому в приемнике образуется нулевая точка N (нейтраль). Нулевая точка источника и приемника могут быть связаны проводом, который называется нулевым или нейтральным. Получается связанная четырехпроводная система электрических цепей.
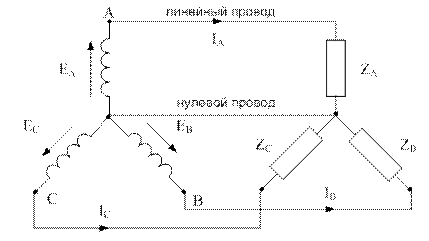
Рисунок 5.14
· Разность потенциалов между линейными зажимами и нейтралью называется фазным напряжением. (Оно отличается от ЭДС на величину падения напряжения в обмотках) (UA,UB,UC).
· Разность потенциалов между парой линейных проводов называется линейным напряжением. (UAВ,UBС,UAC).
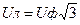
· В фазах источника и приемника текут фазные токи.
· Токи в линейных проводах называют линейными.
Так как при соединении звезда в точках перехода из источника в линию и из линии в приемник нет ответвлений то линейные и фазные токи равны.
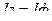
При несимметричной нагрузке, в схеме соединения «звезда» без нулевого провода, в случае замыкания одной из фаз, или обрыва происходит значительное изменение токов и фазных напряжений.
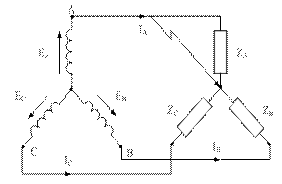
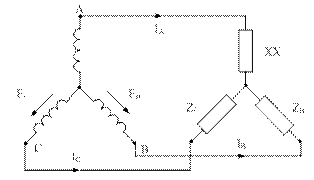
а) б)
Рисунок 5.15
При КЗ например фазы А (рисунок 5.15а) линейный провод этой фазы соединен непосредственно к нулевой точке нагрузки, тогда
Uф в=Uл в; Uф с=Uл с
При обрыве линейного провода в одной из фаз (рисунок 5.15б), в схеме соединения «звезда» без нулевого провода, (ХХ фазы А), напряжения на двух других фазах по величине оказываются равными половине линейного напряжения UBC.
5.4. Соединение треугольником при симметричной нагрузке.
При соединении треугольником из трех обмоток источника образуется замкнутый на себя контур (рисунок 5.16). точно так же замкнутый контур создается из трех фаз приемника. Общие точки двух фаз приемника соединяются между собой линейными проводами. Так образуется связанная трехфазная трехпроводная система.
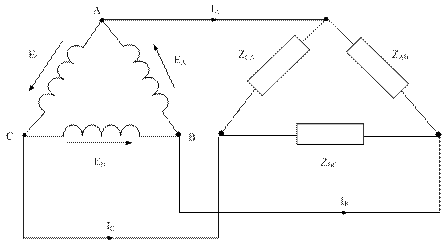
Рисунок 5.16
По второму закону Кирхгофа ЕА+ЕВ+ЕС = 0, при несимметрии системы ЭДС их сумма не равна нулю, поэтому уже при ХХ образуется ток, который может быть большим. При неправильном включении обмоток (начала и конца) сумма ЭДС в контуре равна двойному значению ЭДС в контуре равна двойному значению ЭДС фазы.
Фазные и линейные напряжения совпадают, так как конец одной фазы соединен с началом другой.
Uф = Uл;
Фазные токи отличаются от линейных, так как в точках подключения источников к нагрузкам есть узлы. IA = IAB-IAC ; IB = IBC-IAB ; IC = IAC-IBC;
Действующее значение линейных токов определяется по векторной диаграмме из равнобедренного треугольника IA = 2 IAB cos 30 = IAB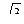 
Iл = Iф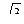
Если нагрузка будет несимметричная, то в случае обрыва одной из фаз Iл = Iф.
5.5 Мощность трехфазной системы.
Мощность системы при любом соединении равна сумме мощностей каждой фазы.
Полная мощность – S = SA+SB+SC+S0 или определяется как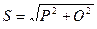 
Активная мощность – это сумма активных мощностей фаз нагрузки и активной мощности в сопротивлении, включенном в нулевой провод.
Р = РА + РВ + РС + Р0
Реактивная мощность системы – это сумма реактивных мощностей фаз нагрузки и реактивной мощности в сопротивлении, включенном в нулевой провод .
Q = QA + QB + QC + Q0
Если нагрузка равномерная, то Р0 = Q0 = 0, PA= PB = PC = IфUф cos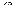 
;
QA = QB = QC = IфUф sin 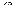, где, 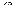угол между напряжением Uф и током Iф.
S = 3 Iф Uф = 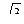IлUл
5.6 Расчет трехфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и поэтому если нагрузка симметричная, то расчет и исследование процессов в них производят теми же методами и приемами, что рассматривались в разделе 5.3; 5.4. построение векторных диаграмм облегчает нахождение углов между токами и напряжениями, позволяет провести проверку расчетов. Расчет трехфазной цепи в симметричном режиме сводится к расчету для одной фазы. Если режим работы несимметричный, то для расчета системы применяются методы расчета сложных цепей. Рассмотрим примеры расчета трехфазных цепей.
Пример 5.1
В цепь трехфазного тока с линейным напряжением Uл = 220 В включена треугольником нагрузка. Сопротивление фаз одинаковое RAB = RBC = RCA = 100 Ом. Определить фазное напряжение, линейный и фазный токи. Построить векторную диаграмму. Схема устройства изображена на рисунке 5.20 а.
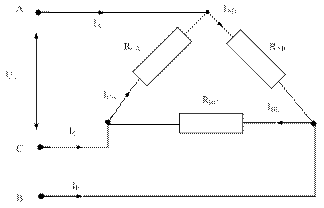
а) б)
Рисунок 5.17
Так как, требуется рассчитать симметричную схему RAB = RBC = RCA, то решение сводится к расчету одной фазы.
1. При соединении фаз треугольником Uл = Uф = 220 В.
2. Фазные токи определяются по закону Ома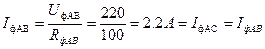 
3. Линейные токи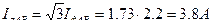 
4. Потребляемая мощность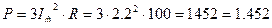 
кВт
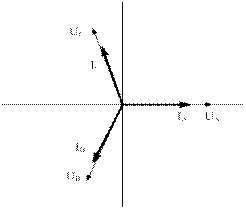
5. Построим векторную диаграмму. Так как, в трехфазной системе действуют три напряжения, сдвинутые на 1200, то пример UА =220 В, UВ = 220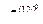 
В,
UС = 220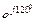 
В. Нагрузка имеет резистивный характер, поэтому токи будут совпадать по фазе напряжением. Выберем масштаб по напряжению МU 100 В/см, по току МI 2 А/см (рисунок 5.17 б).
Пример 5.2
В трехфазную цепь с линейным напряжением (рис.5.18) 220В включен приемник, соединенный треугольник. Сопротивлением каждой фазы равно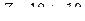 
. Найти фазные и линейные токи.
Решение:
1. Расчет проводится комплексным методом. Примем, что вектор напряжения UAB направлен по действительной оси, тогда: UAB = UA= 220B; UBC = UB = 220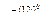 
B;
UCA = UC = 220 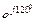B.
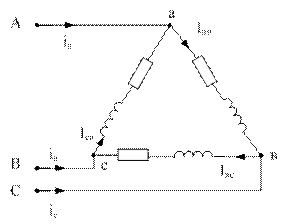
Рисунок 5.18
2. Определим фазные токи:
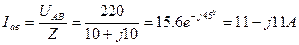
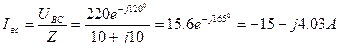
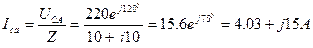
3. Составим уравнения для определения линейных токов (по 1 закону Кирхгофа) и определим:
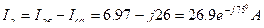
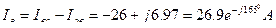
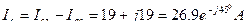
Вопросы для самоконтроля:
1. Какие цепи называются трехфазными?
2. Какие токи и напряжения называются линейными?
3. Какое соединение фаз называется звездой?
4. Для чего нужен нулевой провод?
5. Какое соединение фаз называется треугольником?
2 Модуль. Магнитные цепи и электромагнитные устройства – ПК-3:
Тема №1: Трансформаторы
Электромагнетизм
Тема посвящена рассмотрению основных законов электромагнитных явлений. Необходимо усвоить, что в пространстве, окружающем проводники с током, обнаруживаются особые явления, обусловленные наличием электромагнитного поля.
Магнитное поле
Магнитным полем называется одна из форм электромагнитного поля, возбуждаемая движущимися электрическими зарядами и характеризующаяся силовым воздействием на движущиеся заряженные частицы.
Направление магнитного поля связано с направлением тока. Графически магнитное поле изображается магнитными линиями, которые замкнуты и проводятся так, чтобы направление касательной в каждой точке линии совпадало с направлением поля.
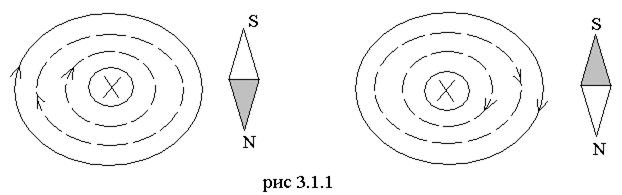
Магнитное поле прямолинейного проводника с током имеет вид концентрических окружностей и направление его силовых линий определяется по «правилу буравчика», если ввинчивать буравчик в провод, то направление вращения его рукоятки будет совпадать с направлением магнитных силовых линий (рис. 3.1.1).
Параметры магнитного поля
Интенсивность магнитного поля характеризуется параметрами: напряженность, магнитная индукция, магнитный поток.
Напряженностью магнитного поля называется векторная величина, характеризующая интенсивность магнитного поля в данной его точке.
Напряженность в пространстве, окружающем проводник с током, вычисляется по формуле:
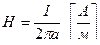
где: I – сила тока в проводнике, А
а - расстояние от оси провода до выбранной точки пространства вокруг проводника, м
Напряженность магнитного поля внутри катушки (соленоида) на ее оси, если длина катушки больше диаметра.
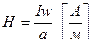
где: w - число витков катушки
С напряженностью связано понятие о намагничивающей силе.
Намагничивающей силой называется величина, характеризующая свойство тока возбуждать магнитное поле (Fm).
Для проводника с током Fm = I.
Так как,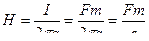 
,
то напряженность магнитного поля – это величина численно равная намагничивающей силе, приходящейся на единицу длины магнитной силовой линии радиуса а.
Векторная величина, характеризующая интенсивность магнитного поля с учетом влияния среды, называется магнитной индукцией.
Величина магнитной индукции определяется по формуле:
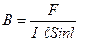или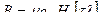 
где: μа – абсолютная магнитная проницаемость среды, Гн/м
μа = μо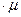 
где: μо – магнитная проницаемость вакуума,
μо =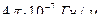 
μ - относительная магнитная проницаемость среды;
F - сила, действующая на проводник с током.
Магнитная индукция в сердечнике катушки
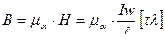
Произведение магнитной индукции В на площадь S поверхности, которую пересекает линии магнитного поля, называется магнитным потоком.
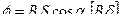
Н и В связаны соотношением 
- угол между направлением вектора В и перпендикуляром к поверхности S.
В сердечнике катушки 
Дата: 2018-12-28, просмотров: 338.
