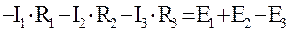Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 или 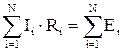.              4.27

Формула 4.27 выражает второе правило Кирхгофа: в замкнутом контуре, произвольно выделенном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов на сопротивление соответствующих участков равна алгебраической сумме ЭДС, действующих в этом контуре.

При составлении уравнений по второму правилу Кирхгофа нужно току и ЭДС приписывать знаки. Если направление обхода контура совпадает с направлением силы тока и ЭДС, то они считаются положительными, в противном случае – отрицательными. Направление обхода контура выбирается произвольно и не зависит от выбора направления в других контурах.

Методы расчета электрических цепей. (V2)
Прежде чем приступить к изучению непосредственно методов расчета, необходимо определить, что есть расчет электрической цепи? Будем читать цепь рассчитанной, если определены токи во всех схемы ветвях. Зная токи и параметры элементов схемы легко можно определить все значения напряжений, мощностей и т.д.
В курсе электротехники изучаются основные методы расчета электрических цепей. К ним относятся:
1. Расчет цепей с непосредственным использованием законов Ома и Кирхгофа.
2. Метод преобразования электрической цепи.
3. Метод контурных токов.
4. Метод узловых потенциалов.
5. Метод эквивалентного генератора (теорема об активном двухполюснике).
6. Метод наложения.
Большинство методов расчета электрических цепей направлено на упрощение процедуры нахождения токов в ветвях схемы. Этого можно достичь несколькими способами. Можно упростить систему уравнений, по которой производится расчет, а в некоторых случаях можно упростить саму схему. Последнее применяется в том случае, когда необходимо определить ток только в одной ветви, а значения токов во всех других ветвях не представляют интереса.

 

Метод уравнений Кирхгофа

Алгоритм расчета. 

1. Определяем число узлов и количество ветвей.

2. Выбираем произвольно направление токов в ветвях и направления обхода контуров (н.о.к).

3. Составляем по законам Кирхгофа систему уравнений, количество которых равно количеству неизвестных токов.

Из них: по I закону Кирхгофа – на единицу меньше числа узлов в схеме, остальные уравнения – по II закону Кирхгофа.

При составлении уравнений по II закону Кирхгофа необходимо учитывать следующее: со знаком «плюс» записываются те ЭДС и токи, направления которых совпадают с направлением обхода контура, со знаком «минус» - не совпадающие с Н.О.К.

4. Подставить числа и решить систему уравнений относительно неизвестных токов.

5. Если в результате расчетов какой-либо ток получился со знаком «минус», значит его действительное значение противоположно выбранному. Действительное направление нужно показать пунктиром на схеме.

 

Пример

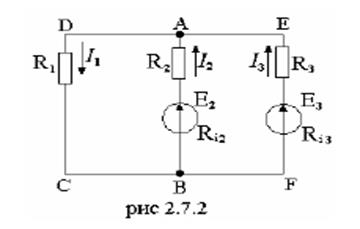
Составить уравнение для расчета цепи, изображенной на рис. 2.7.2.

Решение

1. Определяем число узлов – n = 2 (А и Б), число ветвей – 3 (СД, АБ, EF).

2. Выбираем направление отхода (НОК) и направления токов в ветвях.

3. Составляем 3 уравнения, из них по 1-му закону Кирхгофа (n-1) = 1 уравнение, и остальные два – по II-му закону Кирхгофа.

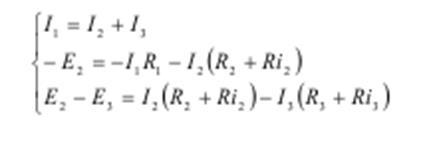
Метод контурных токов

Алгоритм расчета:

1. Произвольно выбираем направление обхода контуров.

2. Выделяем в схеме “m” независимых контуров, в каждом из которых произвольно

выбираем направления контурных токов. (Это расчетный ток, выбираемый

условно).

3. Для определения контурных токов составляем “m” уравнений по II закону

Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в

30 данный контур ( с одной стороны от знака равенства) и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).

4. Действительные токи в ветвях определяются алгебраической суммой контурных токов, проходящих по данной ветви.

Пример 2.7.3.

Составить уравнение по II закону Кирхгофа для решения задачи методом контурных

токов (рис. 2.7.3).

 

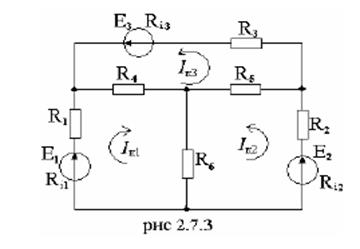
Решение.

1. Составляем три уравнения по II закону Кирхгофа. Направление обхода контуров совмещаем с направлением контурных токов.

 

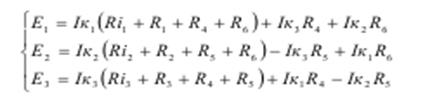
Действительные токи в ветвях определены из соотношений:

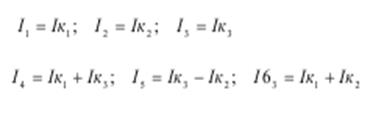
Метод узловых потенциалов

 

Данный метод позволяет определить токи в цепи с помощью (n-1) уравнений, составленных по I закону Кирхгофа, где n – число узлов в схеме.

Алгоритм расчета

1. Обозначить буквами все узлы и потенциалы этих узлов.

2. Задаться предполагаемыми направлениями токов во всех ветвях.

3. Составить (n-1) уравнений по I закону Кирхгофа.

4. Ток в каждой ветви выразить через потенциалы узлов на зажимах ветви, ЭДС и сопротивления данной ветви. Следует помнить, что ток течет от точки с более высоким потенциалом к точке с более низким потенциалом. Если направление ЭДС совпадает с направлением предполагаемого тока, то такая ЭДС записывается со знаком «+», а если противоположно, то со знаком (-).

5. Потенциал одного из узлов принять равным нулю.

6. Подставить числовые значения и рассчитать потенциалы остальных узлов.

7. По известным потенциалам узлов, ЭДС и сопротивлением определить токи во всех ветвях.

8. Выполнить проверки по I закону Кирхгофа.

 

Пример 2.7.4.

Определить значения и направления токов в ветвях методом узловых потенциалов для цепи рис. 2.7.4, если Е1=108 В; Е2=90 В; Ri1=2 Ом; Ri2=1 Ом; R1=28 Ом; R2=39 Ом; R3=60 Ом.

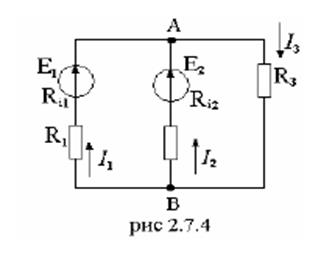
Решение

1. Обозначим на схеме узлы и их потенциалы А; ЧА; В; ЧБ.

2. Зададимся предполагаемым направлением токов в ветвях I1, I2, I3/

3. Составим (n-1) уравнение по I закону Кирхгофа для узла А.

    

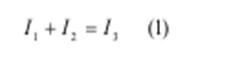
4. Выражаем токи через потенциалы, ЭДС и сопротивления.

                   

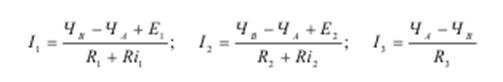
5. Примем ЧА=0

    6. Подставляем полученные выражения токов в уравнение 1.

 

                   

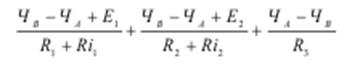
7. Подставим числовые значения и решаем полученное уравнение.

              

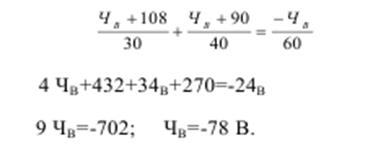
8. Определяем токи в ветвях.

 

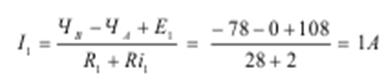
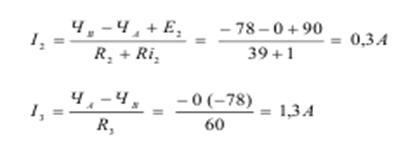
Действительные направления токов совпадают с выбранными.

Двухполюсники и четырёхполюсники. Уравнения и схемы замещения. [Новожилов].

При анализе электрической цепи важное место занимает структура или топология. Такие признаки, как число узлов и контуров, полностью определяют конфигу­рацию цепи. К важным топологическим признакам также относится количест­во полюсов, или внешних выводов цепи. По этому признаку следует выделить: => двухполюсники, к которым относятся цепи с двумя выводами. С помощью двухполюсников моделируются источники и приемники сигналов, на­пример, микрофон, телефон, приемная и передающая антенны; => четырехполюсники, в которых выделены два входа и два выхода, на­пример, трансформатор, усилитель. Они выполняют функции переда­точного звена; => шестиполюсники, представляющие собой передаточные звенья с управляемым коэффициентом передачи.

Цепь с числом полюсов более двух принято называть многополюсни­ком. В теории цепей многополюсники используются для составления топологических уравнений исследуемой цепи, например, уравнений по методу переменных состояния.

Схемы замещения. Для составления схемы за­мещения, или эквивалентной схемы, четырехполюсника с Y-параметрами воспользуемся его уравнениями , из которых следует, что входной и выходной токи содержат две составляющих, одна из которых создается напряжением U_x, другая — напряжением 0₂, при этом:

· составляющие токов Y_uU_l , Y ₂₂ U ₂ можно рассматривать как отклики при воздействии входного и выходного напряжения на двухполюсни­ки Уп, Y ₂ 2, подключенные соответственно к входным 1-1 и выходным 2-2 зажимам четырехполюсника;

· составляющие токов Y_nU ₂ , Y _{2 x} U_x можно рассматривать как источни­ки, управляемые со стороны выходных 2-2 и входных 1-1 зажимов соответственно.

На рис. 4,а приведена схема замещения Y-четырехполюсника, состав­ленная в соответствии с изложенным выше принципом. На рис. 4,б,в,г приведены схемы G-, Н- и Z-четырехполюсников, а также описывающие их уравнения.

Пассивные элементы схем замещения отражают потери в четырехпо­люснике, а источники — возможность усиления мощности. При этом с помощью источника в выходной цепи моделируется полезный эффект усиления, а с помощью источника во входной цепи — паразитный эф­фект передачи мощности из выходной цепи, приводящей к возможному самовозбуждению четырехполюсника. 

Тема №2: Электрические цепи синусоидального тока. Трехфазные цепи. [Электротехника Электронное пособие для тудентов очной и заочной форм обучения всех технических специальностей]

 

Получение синусоидальной электродвижущей силы (ЭДС). Способы представления синусоидальных ЭДС, напряжений и токов. Действующие значения синусоидальных величин. Электрические цепи с резистором, индуктивностью и емкостью. Мощности цепи синусои­дального тока. Коэффициент мощности цепи. Резонансные явления в цепях синусоидального тока, условия возникновения, практическое значение. Комплексный метод расчёта линейных цепей переменного тока.

Переменным электрическим током называется ток, который с течением времени изменяет свое значение и направление.

В электрических сетях используется синусоидальный переменный ток, который возникает в цепи под действием синусоидальной ЭДС.

Переменный ток вырабатывается специальными генераторами, принцип действия которых основан на явлении электромагнитной индукции.

4.1    Параметры переменного тока.

Синусоидальная ЭДС, ток и напряжение характеризуется следующими параметрами:

- мгновенное значение (i,u,e) – значение синусоидальной величины в заданный момент времени.

- амплитуда (I_m,U_m,E_m) – наибольшее из всех мгновенных значений.

- период Т – время в течении которого переменная величина проходит полный цикл колебания и возвращается к исходному значению (время одного колебания).

- частота – количество колебаний в единицу времени

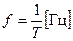
Промышленная частота в России равна 50 Гц.

- угловая частота (угловая скорость) – угол поворота рамки в магнитном поле в единицу времени.

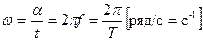
- начальная фаза – угол, определяющий значение синусоидальной величины в начальный момент времени (t=0)

Разность начальных фаз двух синусоидальных величин определяет угол сдвига фаз этих величин.

        

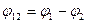
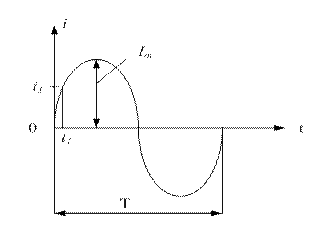
Любая переменная величина имеет свой закон изменения.

Например:

Ток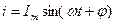  

Напряжение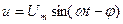   

- действующее значение (I_m,U_m,E_m) – это такое значение постоянного тока, который за время, равное периоду переменного тока на данном резисторе выделяет столько же тепла, сколько переменный ток за то же время.

Действующее и амплитудное значения связаны соотношением:

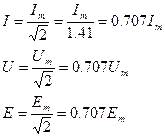
4.1.1. Временные и векторные диаграммы.

График зависимости переменной величины (i,u,e) от времени называется временной или волновой диаграммой.

Если переменная величина появляется раньше начала времени отсчета (начала координат), то она называется опережающей по фазе, угол 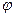 положительный (рис. 4.1.1 а). На графике она начинается левее начала координат.

Если переменная величина появляется позже начала времени отсчета, она называется отстающей по фазе, угол 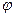 отрицательный. На графике она начинается правее начала координат (рис.4.1.1 б).

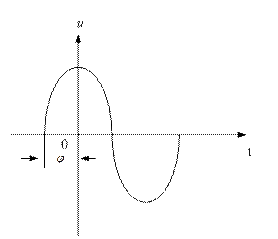
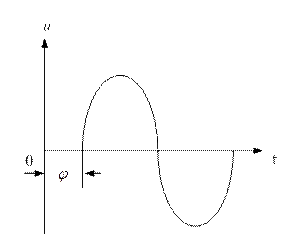
а)                                                                              б)

Рисунок 4.1.1

Совокупность векторов, изображающих синусоидальные величины, называется векторной диаграммой.

Величина, опережающая по фазе, откладывается против часовой стрелки на заданный угол по отношению к горизонтальной оси.

Величина, отстающая по фазе, откладывается по часовой стрелке на заданный угол по отношению к горизонтальной оси.

Пример

Изобразить с помощью векторных диаграмм токи: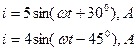

Выбирается масштаб тока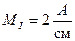

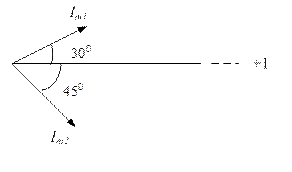
Выразим ток, напряжения, мощность и активного сопротивления в комплексной форме.

 

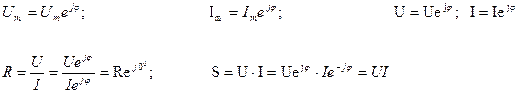
4.2.   Расчет цепей переменного тока с различными элементами.

4.2.1. Цепь с активным сопротивлением (с резистором).

                                                                                                        

К зажимам цепи приложено синусоидальное напряжение

                 

 

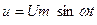
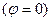
В любой момент ток в цепи определяется по закону Ома:

                  

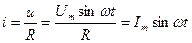
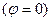
Ток и напряжение в любой момент времени совпадают по фазе.

                                      

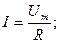
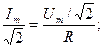
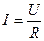
Таким образом, закон Ома справедлив для любых значений тока(мгновенных, амплитудных, действующих).

Мощность в любой момент времени:

              

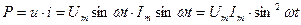
Временная (а) и векторная (б) диаграмма приведены на рисунке 4.2.1

      

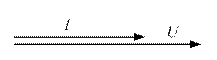
а) Временная диаграмма                                              б) Векторная диаграмма                                               

Выразим ток, напряжения, мощности и активного сопротивления в комплексной форме

; ;

; .

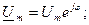
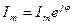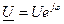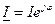
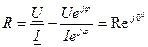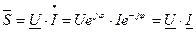Пример:

К цепи переменного тока с активным сопротивлением R= 8 Ом приложено напряжение u = 45 sin( 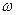t+30°). Определить активную мощность цепи и уравнение мгновенного значения тока.

 

Решение:

1. Действующее значение напряжения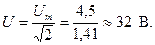

2. Действующий ток в цепи I= .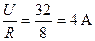

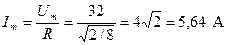3. Мощность цепи P = U∙I = 32∙4 = 128 Вт.

4. Уравнение мгновенного значения тока i = 5,64 sin ( 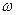t+30°).

4.2.2. Цепь с индуктивностью

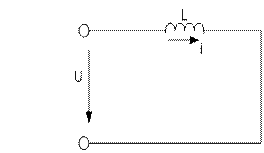
Рис. 4.2.3. а)

Если к указанной катушке приложить синусоидальное напряжение, то в цепи будет протекать синусоидальный ток, переменный магнитный поток которого индуцирует в катушке ЭДС самоиндукции:

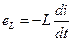
где 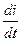 - скорость изменения тока;

=

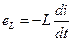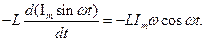
Напишем для цепи, изображенной на рис. 4.2.3. уравнение второго закона Кирхгофа.

Так как, R цепи равно нулю, то iR=0, поэтому u+ 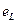=0, откуда и u= -  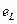т.е. 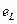 равна и противоположна по направлению напряжению на зажимах цепи. Подставив значение  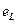в эту формулу получим:

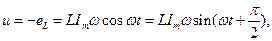
Из этой формулы видно, что напряжение на зажимах цепи опережает по фазе ток на угол 90° или ток отстает по фазе от напряжения на угол 90°. Амплитуда напряжения 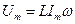, откуда .

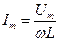Разделив обе части последней формулы на 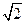, получим выражение для действующего значения тока 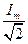= 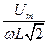; I= .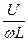

Выведенная формула есть выражение закона Ома для данной цепи, следовательно, 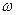L представляет величину сопротивления этой цепи, называемого индуктивным сопротивлением и обозначаемого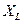

= =

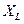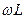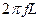
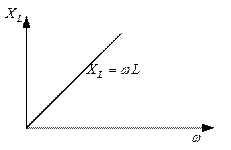Рис. 4.2.3. б)

Из формулы следует, что индуктивное сопротивление цепи пропорционально индуктивности L и угловой частоте переменного тока.

Индуктивным сопротивлением называется величина, характеризующая противодействие ЭДС самоиндукции переменному току.

Выразим значения напряжения, тока и индуктивного сопротивления в комплексной форме.

; .

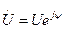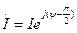Комплекс индуктивного сопротивления найдется так:

 =  =  = .

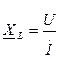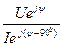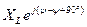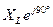В алгебраической форме комплекс 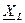 выразится так:

= ,

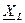Поскольку cos 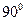=0; sin 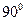=1.