Введение
В данном разделе лекций речь не идет об изучении конкретных электротехнических устройств. В основах теории электрических цепей важно получить ответ на вопросы:
1. В каких зависимостях находятся между собой токи и напряжения на каждом участке электрической цепи? Потому, что именно эти соотношения определяют энергетику устройств.
2. Как наилучшим образом рассчитать электрическую цепь? Так как от выбора метода расчета зависит успех при анализе процессов, протекающих в электроустановках. Поэтому мы будем иметь дело со схемами замещения. Каждое электротехническое устройство может быть описано своей математической моделью, которая должным образом, с теми или иными допущениями, отражает протекание энергетических процессов в ней. На основе данной математической модели строится схема замещения, которая состоит из конечного набора элементов.
Все элементы можно разделить на две группы:
1. Активные элементы или источники электрической энергии.
2. Пассивные элементы или потребители электрической энергии.
К первой группе относятся источники тока и напряжения.
Ко второй группе относятся активные и реактивные потребители.
Графические изображения элементов и их основные параметры показаны в таблице.
| Элемент | Графичес кое изо бражение | Параметр | Ед. измерения | Дополнительные ед. измерения |
| 1 | 2 | 3 | 4 | 5 |
| Источник ЭДС | 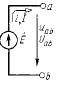
| ЕДС | Вольт (В) | - |
| Источник тока | 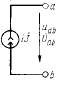
| Ток | Ампер (А) | - |
| Резистивный элемент (резистор) | 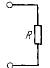
| Сопротивление | Ом (Ом) | 1 кОм=103 Ом 1 мОм=106 Ом 1 гОм=109 Ом |
| Индуктивный элемент (катушка индуктивности) | 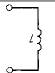
| Индуктивность | Генри (Гн) | 1 мГн=10-3 Гн 1 мкГн=10-6 Гн |
| Емкостной элемент (конденсатор) | 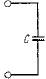
| Емкость | Фарада (Ф) | 1 мкФ=10-6 Ф 1 нФ=10-9 Ф 1 пФ=10-12 Ф |
1. Модуль Электрические цепи – ПК-3
Тема №1: Электрические цепи постоянного тока
. Электрический ток. Необходимые условия существования тока.
Электрическим током называется любое упорядоченное движение электрических зарядов. Если в проводнике создать электрическое поле, то в нем свободные электрические заряды придут в движение – возникает ток, называемый током проводимости. Если в пространстве перемещается заряженное тело, то ток называется конвекционным. За направление тока принимается направление движения положительно заряженных частиц.
Для возникновения и существования тока необходимо с одной стороны, наличие свободных заряженных частиц, а с другой – наличие электрического поля в проводнике. Количественной характеристикой служит величина I называемая силой тока и определяемая зарядом, протекающим через поперечное сечение проводника в единицу времени,
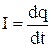 . 4.1
. 4.1
Сила тока величина скалярная, измеряется в амперах.
Электрический ток может быть распределен по поверхности, сквозь которую он протекает, неравномерно. Более детально ток можно характеризовать с помощью вектора плотности тока 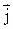 . Он численно равен силе тока, протекающей через единичную площадку, перпендикулярную к направлению движения зарядов
. Он численно равен силе тока, протекающей через единичную площадку, перпендикулярную к направлению движения зарядов
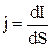 . 4.2
. 4.2
Зная вектор плотности тока в каждой точке поверхности можно найти силу тока через эту поверхность
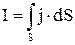 . 4.3
. 4.3
Пусть заряд свободной частицы равен 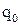 , концентрация свободных зарядов равна n, скорость их упорядоченного движения
, концентрация свободных зарядов равна n, скорость их упорядоченного движения 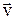 . Тогда за время
. Тогда за время 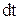 через поперечное сечение проводника будет переноситься заряд
через поперечное сечение проводника будет переноситься заряд 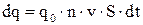 . Учитывая 4.1 и 4.2, для плотности тока получим выражение:
. Учитывая 4.1 и 4.2, для плотности тока получим выражение:
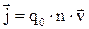 . 4.4
. 4.4
Так как скорость 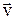 является вектором, то и плотность тока также будет вектором.
является вектором, то и плотность тока также будет вектором.
2.4.3. Закон Ома для участка цепи. Дифференциальная форма закона Ома.
Г. Ом на опыте установил, что сила тока в однородном проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна его сопротивлению
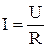 . 4.5
. 4.5
Величина R называется электрическим сопротивлением проводника и зависит от его геометрических размеров, свойств материала, из которого он изготовлен и температуры
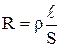 , 4.6
, 4.6
где 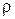 - удельное сопротивление, величина численно равная сопротивлению куба вещества с ребром 1 м, при условии, что ток течет в направлении перпендикулярном граням куба.
- удельное сопротивление, величина численно равная сопротивлению куба вещества с ребром 1 м, при условии, что ток течет в направлении перпендикулярном граням куба.
Закон Ома можно записать в дифференциальной форме. Рассмотрим цилиндрический проводник длиной 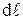 и площадью поперечного сечения
и площадью поперечного сечения 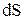 . Напряжение приложенное к проводнику
. Напряжение приложенное к проводнику 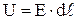 , где Е – напряженность поля в проводнике. Наконец, сопротивление проводника по 4.6 равно
, где Е – напряженность поля в проводнике. Наконец, сопротивление проводника по 4.6 равно 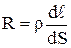 . Подставляя эти значения в 4.5, получим
. Подставляя эти значения в 4.5, получим
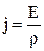 . 4.7
. 4.7
Носители заряда движутся в направлении вектора Е и поэтому направление векторов 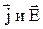 совпадают. Таким образом, окончательно, можно получить:
совпадают. Таким образом, окончательно, можно получить:
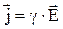 , 4.8
, 4.8
где 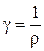 - удельная проводимость вещества.
- удельная проводимость вещества.
Формула 4.8 выражает закон Ома в дифференциальной форме.
3.4.3. Источники тока. Сторонние силы. ЭДС источника тока.
Если два разноименно заряженных тела соединить проводником, то в нем возникает электрический ток. Возникновение тока приводит к тому, что поле очень быстро исчезает и, следовательно, ток прекращается. Для того, чтобы поддерживать ток достаточно длительное время нужно от тела с меньшим потенциалом непрерывно отводить приносимые заряды, а к телу с большим потенциалом непрерывно их подводить. Иными словами электрическая цепь должна быть замкнутой. Но электрическое поле не может перемещать заряды по замкнутому пути 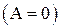 и поэтому наряду с электрическими силами на перемещающиеся заряды должны действовать и силы не электростатического характера, так называемые сторонние силы.
и поэтому наряду с электрическими силами на перемещающиеся заряды должны действовать и силы не электростатического характера, так называемые сторонние силы.
Величину равную работе сторонних сил по перемещению единичного положительного заряда называют электродвижущей силой источника (ЭДС)
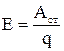 . 4.9
. 4.9
По аналогии с электрическими силами стороннюю силу можно представить в виде:
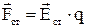 , 4.10
, 4.10
где 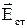 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.
Тогда 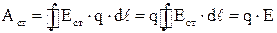 и, следовательно,
и, следовательно,

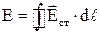 . 4.11
. 4.11
Рассмотрим неоднородный участок цепи 1 – 2 (рис.22). На участке 1-2 на заряды будут действовать две силы: электрическая сила 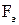 и сторонняя сила
и сторонняя сила 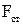 и их результирующая
и их результирующая 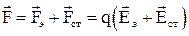 . Тогда работа по перемещению заряда между точками 1 и 2 будет определяться по формуле:
. Тогда работа по перемещению заряда между точками 1 и 2 будет определяться по формуле:
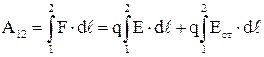 . 4.12
. 4.12
Но 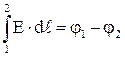 , а
, а 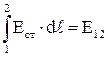 , и тогда
, и тогда 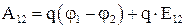 . 4.13
. 4.13
Величину 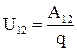 называют напряжением между двумя точками электрической цепи
называют напряжением между двумя точками электрической цепи
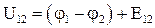 . 4.14
. 4.14
При отсутствии источника тока 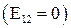 напряжение
напряжение 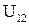 совпадает с разностью потенциалов.
совпадает с разностью потенциалов.
4.4.3. Работа и мощность постоянного тока. Закон Джоуля - Ленца.
При упорядоченном перемещении электрических зарядов электрическое поле совершает работу 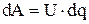 . Из 4.1 найдем, что
. Из 4.1 найдем, что 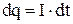 и тогда
и тогда 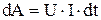 . После интегрирования можно получить
. После интегрирования можно получить
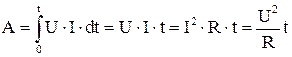 . 4.15
. 4.15
Следовательно, для мощности тока получим:
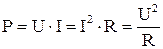 . 4.16
. 4.16
При прохождении тока по проводнику он нагревается. Джоуль и Ленц установили, что количество теплоты, выделяющееся в проводнике, может быть найдено по формуле:
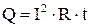 . 4.17
. 4.17
 Если сила тока изменяется во времени, то закон Джоуля-Ленца можно записать в виде:
Если сила тока изменяется во времени, то закон Джоуля-Ленца можно записать в виде:
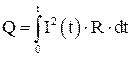 . 4.18
. 4.18
Закон Джоуля – Ленца можно записать в дифференциальной форме. Выделим в проводнике с током I элементарный объем в форме цилиндра длиной 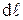 и площадью поперечного сечения
и площадью поперечного сечения 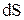 . Согласно закону Джоуля – Ленца 4.17 в нем будет выделяться количество теплоты:
. Согласно закону Джоуля – Ленца 4.17 в нем будет выделяться количество теплоты:
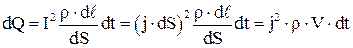 . 4.19
. 4.19
Количество теплоты, отнесенное к единице объема и единице времени, называется удельной тепловой мощностью тока
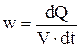 . 4.20
. 4.20
Учитывая 4.19 выражение 4.20 примет вид
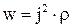 . 4.21
. 4.21
Воспользовавшись соотношением 4.8 выражение 4.21 можно записать в виде:
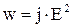 . 4.22
. 4.22
Формулы 4.21 и 4.22 выражают закон Джоуля – Ленца в дифференциальной форме.
5.4.3. Закон Ома для неоднородного участка цепи.
Чтобы получить закон Ома для неоднородного участка цепи, т.е. участка на котором действует ЭДС, воспользуемся законом сохранения энергии. Пусть на концах участка 1 – 2 (рис. 22) поддерживается разность потенциалов 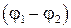 . Обозначим ЭДС, действующую на участке
. Обозначим ЭДС, действующую на участке 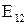 , и зададим направление тока и ЭДС.
, и зададим направление тока и ЭДС.
Если проводник неподвижен, то единственным результатом протекания тока будет его нагревание. Количество теплоты, выделяющееся в проводнике, определяется по закону Джоуля – Ленца 4.17:
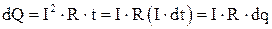 . 4.23
. 4.23
При перемещении электрического заряда совершается работа
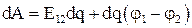 . 4.24
. 4.24
Согласно закону сохранения энергии 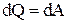 и тогда
и тогда
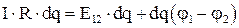
и после сокращения на 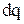 окончательно получим
окончательно получим
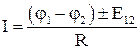 . 4.25
. 4.25
Формула 4.25 выражает закон Ома для неоднородного участка цепи. Из 4.25 следуют частные случаи:
1. Если 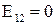 , то
, то 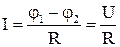 закон Ома для однородного участка цепи.
закон Ома для однородного участка цепи.
2. Если цепь замкнута 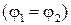 , то
, то  закон Ома для замкнутой цепи.
закон Ома для замкнутой цепи.
6.4.3. Разветвленные цепи. Правила Кирхгофа.
 Закон Ома для неоднородного участка цепи позволяет рассчитать любую электрическую цепь, но расчет этот довольно сложен. Расчет электрических цепей значительно упрощается, если воспользоваться правилами Кирхгофа.
Закон Ома для неоднородного участка цепи позволяет рассчитать любую электрическую цепь, но расчет этот довольно сложен. Расчет электрических цепей значительно упрощается, если воспользоваться правилами Кирхгофа.
 Назовем узлом электрической цепи точку, в которой сходится не менее трех проводников (рис. 23). Токи, втекающие в узел, будем считать положительными, а вытекающие – отрицательными и тогда для узла (рис. 23), получим:
Назовем узлом электрической цепи точку, в которой сходится не менее трех проводников (рис. 23). Токи, втекающие в узел, будем считать положительными, а вытекающие – отрицательными и тогда для узла (рис. 23), получим:
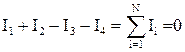 . 4.26
. 4.26
Это и есть первое правило Кирхгофа – алгебраическая сумма токов сходящихся в узле равна нулю. Первое правило Кирхгофа вытекает из закона сохранения электрического заряда.
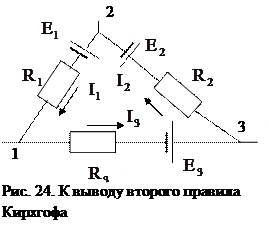
Второе правило Кирхгофа является следствием закона сохранения энергии. Выделим в разветвленной электрической цепи замкнутый контур 1-2-3 (рисю 24). Зададим направление обхода контура (например, по часовой стрелке) и применим к каждому из участков закон Ома для неоднородного участка цепи:

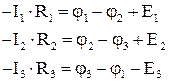
Дата: 2018-12-28, просмотров: 421.