Модуль. Магнитные цепи и электромагнитные устройства – ПК-3:
Тема №1: Трансформаторы 59
Тема №2: Электрические машины [Яцкевич] 66
3. Модуль. Электроника – ПК-3
Тема №1: Электронные приборы [Джонс] 79
Тема №2: Электронные устройства. 104
Библиографический список 144
Введение
В данном разделе лекций речь не идет об изучении конкретных электротехнических устройств. В основах теории электрических цепей важно получить ответ на вопросы:
1. В каких зависимостях находятся между собой токи и напряжения на каждом участке электрической цепи? Потому, что именно эти соотношения определяют энергетику устройств.
2. Как наилучшим образом рассчитать электрическую цепь? Так как от выбора метода расчета зависит успех при анализе процессов, протекающих в электроустановках. Поэтому мы будем иметь дело со схемами замещения. Каждое электротехническое устройство может быть описано своей математической моделью, которая должным образом, с теми или иными допущениями, отражает протекание энергетических процессов в ней. На основе данной математической модели строится схема замещения, которая состоит из конечного набора элементов.
Все элементы можно разделить на две группы:
1. Активные элементы или источники электрической энергии.
2. Пассивные элементы или потребители электрической энергии.
К первой группе относятся источники тока и напряжения.
Ко второй группе относятся активные и реактивные потребители.
Графические изображения элементов и их основные параметры показаны в таблице.
| Элемент | Графичес кое изо бражение | Параметр | Ед. измерения | Дополнительные ед. измерения |
| 1 | 2 | 3 | 4 | 5 |
| Источник ЭДС | 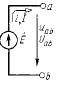
| ЕДС | Вольт (В) | - |
| Источник тока | 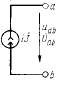
| Ток | Ампер (А) | - |
| Резистивный элемент (резистор) | 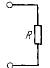
| Сопротивление | Ом (Ом) | 1 кОм=103 Ом 1 мОм=106 Ом 1 гОм=109 Ом |
| Индуктивный элемент (катушка индуктивности) | 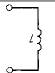
| Индуктивность | Генри (Гн) | 1 мГн=10-3 Гн 1 мкГн=10-6 Гн |
| Емкостной элемент (конденсатор) | 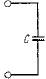
| Емкость | Фарада (Ф) | 1 мкФ=10-6 Ф 1 нФ=10-9 Ф 1 пФ=10-12 Ф |
1. Модуль Электрические цепи – ПК-3
Тема №1: Электрические цепи постоянного тока
. Электрический ток. Необходимые условия существования тока.
Электрическим током называется любое упорядоченное движение электрических зарядов. Если в проводнике создать электрическое поле, то в нем свободные электрические заряды придут в движение – возникает ток, называемый током проводимости. Если в пространстве перемещается заряженное тело, то ток называется конвекционным. За направление тока принимается направление движения положительно заряженных частиц.
Для возникновения и существования тока необходимо с одной стороны, наличие свободных заряженных частиц, а с другой – наличие электрического поля в проводнике. Количественной характеристикой служит величина I называемая силой тока и определяемая зарядом, протекающим через поперечное сечение проводника в единицу времени,
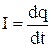 . 4.1
. 4.1
Сила тока величина скалярная, измеряется в амперах.
Электрический ток может быть распределен по поверхности, сквозь которую он протекает, неравномерно. Более детально ток можно характеризовать с помощью вектора плотности тока 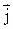 . Он численно равен силе тока, протекающей через единичную площадку, перпендикулярную к направлению движения зарядов
. Он численно равен силе тока, протекающей через единичную площадку, перпендикулярную к направлению движения зарядов
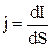 . 4.2
. 4.2
Зная вектор плотности тока в каждой точке поверхности можно найти силу тока через эту поверхность
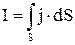 . 4.3
. 4.3
Пусть заряд свободной частицы равен 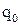 , концентрация свободных зарядов равна n, скорость их упорядоченного движения
, концентрация свободных зарядов равна n, скорость их упорядоченного движения 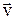 . Тогда за время
. Тогда за время 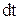 через поперечное сечение проводника будет переноситься заряд
через поперечное сечение проводника будет переноситься заряд 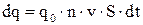 . Учитывая 4.1 и 4.2, для плотности тока получим выражение:
. Учитывая 4.1 и 4.2, для плотности тока получим выражение:
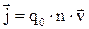 . 4.4
. 4.4
Так как скорость 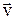 является вектором, то и плотность тока также будет вектором.
является вектором, то и плотность тока также будет вектором.
2.4.3. Закон Ома для участка цепи. Дифференциальная форма закона Ома.
Г. Ом на опыте установил, что сила тока в однородном проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна его сопротивлению
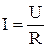 . 4.5
. 4.5
Величина R называется электрическим сопротивлением проводника и зависит от его геометрических размеров, свойств материала, из которого он изготовлен и температуры
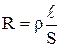 , 4.6
, 4.6
где 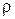 - удельное сопротивление, величина численно равная сопротивлению куба вещества с ребром 1 м, при условии, что ток течет в направлении перпендикулярном граням куба.
- удельное сопротивление, величина численно равная сопротивлению куба вещества с ребром 1 м, при условии, что ток течет в направлении перпендикулярном граням куба.
Закон Ома можно записать в дифференциальной форме. Рассмотрим цилиндрический проводник длиной 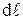 и площадью поперечного сечения
и площадью поперечного сечения 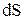 . Напряжение приложенное к проводнику
. Напряжение приложенное к проводнику 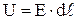 , где Е – напряженность поля в проводнике. Наконец, сопротивление проводника по 4.6 равно
, где Е – напряженность поля в проводнике. Наконец, сопротивление проводника по 4.6 равно 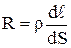 . Подставляя эти значения в 4.5, получим
. Подставляя эти значения в 4.5, получим
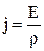 . 4.7
. 4.7
Носители заряда движутся в направлении вектора Е и поэтому направление векторов 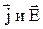 совпадают. Таким образом, окончательно, можно получить:
совпадают. Таким образом, окончательно, можно получить:
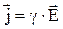 , 4.8
, 4.8
где 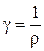 - удельная проводимость вещества.
- удельная проводимость вещества.
Формула 4.8 выражает закон Ома в дифференциальной форме.
3.4.3. Источники тока. Сторонние силы. ЭДС источника тока.
Если два разноименно заряженных тела соединить проводником, то в нем возникает электрический ток. Возникновение тока приводит к тому, что поле очень быстро исчезает и, следовательно, ток прекращается. Для того, чтобы поддерживать ток достаточно длительное время нужно от тела с меньшим потенциалом непрерывно отводить приносимые заряды, а к телу с большим потенциалом непрерывно их подводить. Иными словами электрическая цепь должна быть замкнутой. Но электрическое поле не может перемещать заряды по замкнутому пути 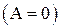 и поэтому наряду с электрическими силами на перемещающиеся заряды должны действовать и силы не электростатического характера, так называемые сторонние силы.
и поэтому наряду с электрическими силами на перемещающиеся заряды должны действовать и силы не электростатического характера, так называемые сторонние силы.
Величину равную работе сторонних сил по перемещению единичного положительного заряда называют электродвижущей силой источника (ЭДС)
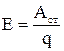 . 4.9
. 4.9
По аналогии с электрическими силами стороннюю силу можно представить в виде:
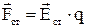 , 4.10
, 4.10
где 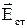 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.
Тогда 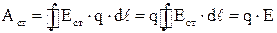 и, следовательно,
и, следовательно,

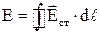 . 4.11
. 4.11
Рассмотрим неоднородный участок цепи 1 – 2 (рис.22). На участке 1-2 на заряды будут действовать две силы: электрическая сила 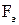 и сторонняя сила
и сторонняя сила 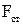 и их результирующая
и их результирующая 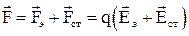 . Тогда работа по перемещению заряда между точками 1 и 2 будет определяться по формуле:
. Тогда работа по перемещению заряда между точками 1 и 2 будет определяться по формуле:
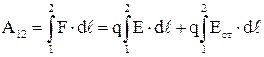 . 4.12
. 4.12
Но 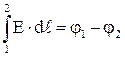 , а
, а 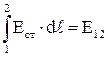 , и тогда
, и тогда 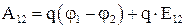 . 4.13
. 4.13
Величину 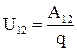 называют напряжением между двумя точками электрической цепи
называют напряжением между двумя точками электрической цепи
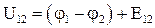 . 4.14
. 4.14
При отсутствии источника тока 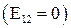 напряжение
напряжение 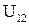 совпадает с разностью потенциалов.
совпадает с разностью потенциалов.
4.4.3. Работа и мощность постоянного тока. Закон Джоуля - Ленца.
При упорядоченном перемещении электрических зарядов электрическое поле совершает работу 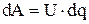 . Из 4.1 найдем, что
. Из 4.1 найдем, что 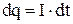 и тогда
и тогда 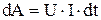 . После интегрирования можно получить
. После интегрирования можно получить
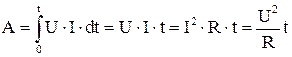 . 4.15
. 4.15
Следовательно, для мощности тока получим:
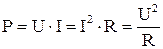 . 4.16
. 4.16
При прохождении тока по проводнику он нагревается. Джоуль и Ленц установили, что количество теплоты, выделяющееся в проводнике, может быть найдено по формуле:
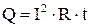 . 4.17
. 4.17
 Если сила тока изменяется во времени, то закон Джоуля-Ленца можно записать в виде:
Если сила тока изменяется во времени, то закон Джоуля-Ленца можно записать в виде:
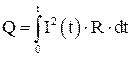 . 4.18
. 4.18
Закон Джоуля – Ленца можно записать в дифференциальной форме. Выделим в проводнике с током I элементарный объем в форме цилиндра длиной 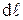 и площадью поперечного сечения
и площадью поперечного сечения 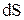 . Согласно закону Джоуля – Ленца 4.17 в нем будет выделяться количество теплоты:
. Согласно закону Джоуля – Ленца 4.17 в нем будет выделяться количество теплоты:
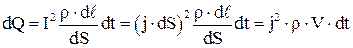 . 4.19
. 4.19
Количество теплоты, отнесенное к единице объема и единице времени, называется удельной тепловой мощностью тока
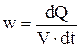 . 4.20
. 4.20
Учитывая 4.19 выражение 4.20 примет вид
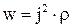 . 4.21
. 4.21
Воспользовавшись соотношением 4.8 выражение 4.21 можно записать в виде:
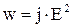 . 4.22
. 4.22
Формулы 4.21 и 4.22 выражают закон Джоуля – Ленца в дифференциальной форме.
5.4.3. Закон Ома для неоднородного участка цепи.
Чтобы получить закон Ома для неоднородного участка цепи, т.е. участка на котором действует ЭДС, воспользуемся законом сохранения энергии. Пусть на концах участка 1 – 2 (рис. 22) поддерживается разность потенциалов 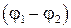 . Обозначим ЭДС, действующую на участке
. Обозначим ЭДС, действующую на участке 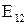 , и зададим направление тока и ЭДС.
, и зададим направление тока и ЭДС.
Если проводник неподвижен, то единственным результатом протекания тока будет его нагревание. Количество теплоты, выделяющееся в проводнике, определяется по закону Джоуля – Ленца 4.17:
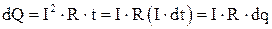 . 4.23
. 4.23
При перемещении электрического заряда совершается работа
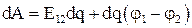 . 4.24
. 4.24
Согласно закону сохранения энергии 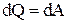 и тогда
и тогда
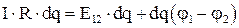
и после сокращения на 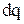 окончательно получим
окончательно получим
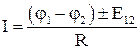 . 4.25
. 4.25
Формула 4.25 выражает закон Ома для неоднородного участка цепи. Из 4.25 следуют частные случаи:
1. Если 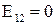 , то
, то 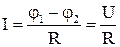 закон Ома для однородного участка цепи.
закон Ома для однородного участка цепи.
2. Если цепь замкнута 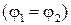 , то
, то  закон Ома для замкнутой цепи.
закон Ома для замкнутой цепи.
6.4.3. Разветвленные цепи. Правила Кирхгофа.
 Закон Ома для неоднородного участка цепи позволяет рассчитать любую электрическую цепь, но расчет этот довольно сложен. Расчет электрических цепей значительно упрощается, если воспользоваться правилами Кирхгофа.
Закон Ома для неоднородного участка цепи позволяет рассчитать любую электрическую цепь, но расчет этот довольно сложен. Расчет электрических цепей значительно упрощается, если воспользоваться правилами Кирхгофа.
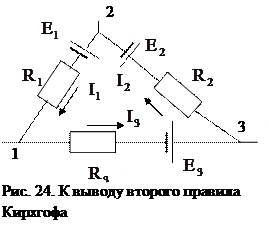 Назовем узлом электрической цепи точку, в которой сходится не менее трех проводников (рис. 23). Токи, втекающие в узел, будем считать положительными, а вытекающие – отрицательными и тогда для узла (рис. 23), получим:
Назовем узлом электрической цепи точку, в которой сходится не менее трех проводников (рис. 23). Токи, втекающие в узел, будем считать положительными, а вытекающие – отрицательными и тогда для узла (рис. 23), получим:
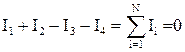 . 4.26
. 4.26
Это и есть первое правило Кирхгофа – алгебраическая сумма токов сходящихся в узле равна нулю. Первое правило Кирхгофа вытекает из закона сохранения электрического заряда.
Второе правило Кирхгофа является следствием закона сохранения энергии. Выделим в разветвленной электрической цепи замкнутый контур 1-2-3 (рисю 24). Зададим направление обхода контура (например, по часовой стрелке) и применим к каждому из участков закон Ома для неоднородного участка цепи:

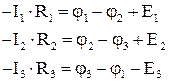
Метод уравнений Кирхгофа
Алгоритм расчета.
1. Определяем число узлов и количество ветвей.
2. Выбираем произвольно направление токов в ветвях и направления обхода контуров (н.о.к).
3. Составляем по законам Кирхгофа систему уравнений, количество которых равно количеству неизвестных токов.
Из них: по I закону Кирхгофа – на единицу меньше числа узлов в схеме, остальные уравнения – по II закону Кирхгофа.
При составлении уравнений по II закону Кирхгофа необходимо учитывать следующее: со знаком «плюс» записываются те ЭДС и токи, направления которых совпадают с направлением обхода контура, со знаком «минус» - не совпадающие с Н.О.К.
4. Подставить числа и решить систему уравнений относительно неизвестных токов.
5. Если в результате расчетов какой-либо ток получился со знаком «минус», значит его действительное значение противоположно выбранному. Действительное направление нужно показать пунктиром на схеме.
Пример
Составить уравнение для расчета цепи, изображенной на рис. 2.7.2.
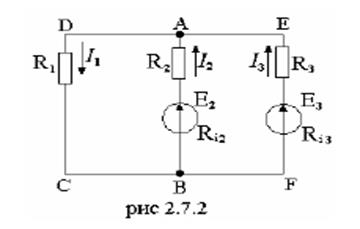
Решение
1. Определяем число узлов – n = 2 (А и Б), число ветвей – 3 (СД, АБ, EF).
2. Выбираем направление отхода (НОК) и направления токов в ветвях.
3. Составляем 3 уравнения, из них по 1-му закону Кирхгофа (n-1) = 1 уравнение, и остальные два – по II-му закону Кирхгофа.
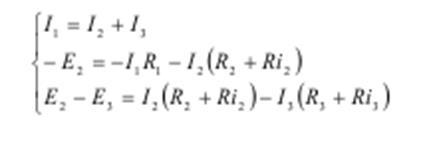
Метод контурных токов
Алгоритм расчета:
1. Произвольно выбираем направление обхода контуров.
2. Выделяем в схеме “m” независимых контуров, в каждом из которых произвольно
выбираем направления контурных токов. (Это расчетный ток, выбираемый
условно).
3. Для определения контурных токов составляем “m” уравнений по II закону
Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в
30 данный контур ( с одной стороны от знака равенства) и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).
4. Действительные токи в ветвях определяются алгебраической суммой контурных токов, проходящих по данной ветви.
Пример 2.7.3.
Составить уравнение по II закону Кирхгофа для решения задачи методом контурных
токов (рис. 2.7.3).
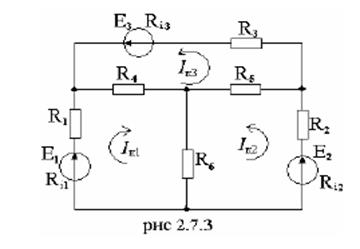
Решение.
1. Составляем три уравнения по II закону Кирхгофа. Направление обхода контуров совмещаем с направлением контурных токов.
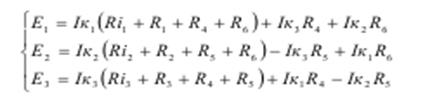
Действительные токи в ветвях определены из соотношений:
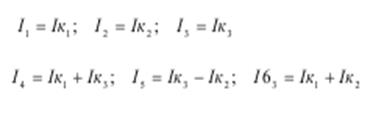
Метод узловых потенциалов
Данный метод позволяет определить токи в цепи с помощью (n-1) уравнений, составленных по I закону Кирхгофа, где n – число узлов в схеме.
Алгоритм расчета
1. Обозначить буквами все узлы и потенциалы этих узлов.
2. Задаться предполагаемыми направлениями токов во всех ветвях.
3. Составить (n-1) уравнений по I закону Кирхгофа.
4. Ток в каждой ветви выразить через потенциалы узлов на зажимах ветви, ЭДС и сопротивления данной ветви. Следует помнить, что ток течет от точки с более высоким потенциалом к точке с более низким потенциалом. Если направление ЭДС совпадает с направлением предполагаемого тока, то такая ЭДС записывается со знаком «+», а если противоположно, то со знаком (-).
5. Потенциал одного из узлов принять равным нулю.
6. Подставить числовые значения и рассчитать потенциалы остальных узлов.
7. По известным потенциалам узлов, ЭДС и сопротивлением определить токи во всех ветвях.
8. Выполнить проверки по I закону Кирхгофа.
Пример 2.7.4.
Определить значения и направления токов в ветвях методом узловых потенциалов для цепи рис. 2.7.4, если Е1=108 В; Е2=90 В; Ri1=2 Ом; Ri2=1 Ом; R1=28 Ом; R2=39 Ом; R3=60 Ом.
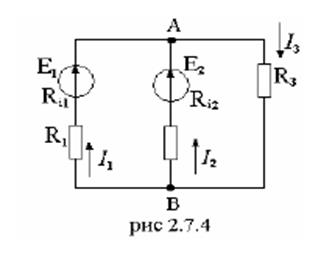
Решение
1. Обозначим на схеме узлы и их потенциалы А; ЧА; В; ЧБ.
2. Зададимся предполагаемым направлением токов в ветвях I1, I2, I3/
3. Составим (n-1) уравнение по I закону Кирхгофа для узла А.
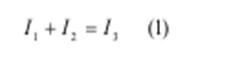
4. Выражаем токи через потенциалы, ЭДС и сопротивления.
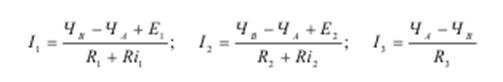
5. Примем ЧА=0
6. Подставляем полученные выражения токов в уравнение 1.
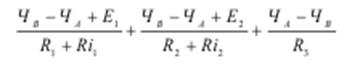
7. Подставим числовые значения и решаем полученное уравнение.
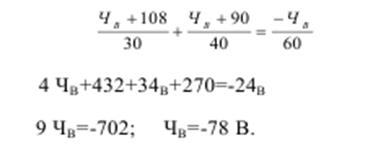
8. Определяем токи в ветвях.
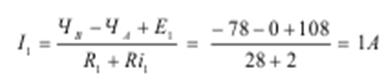
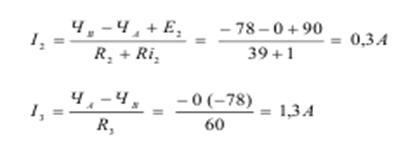
Действительные направления токов совпадают с выбранными.
Двухполюсники и четырёхполюсники. Уравнения и схемы замещения. [Новожилов].
При анализе электрической цепи важное место занимает структура или топология. Такие признаки, как число узлов и контуров, полностью определяют конфигурацию цепи. К важным топологическим признакам также относится количество полюсов, или внешних выводов цепи. По этому признаку следует выделить: => двухполюсники, к которым относятся цепи с двумя выводами. С помощью двухполюсников моделируются источники и приемники сигналов, например, микрофон, телефон, приемная и передающая антенны; => четырехполюсники, в которых выделены два входа и два выхода, например, трансформатор, усилитель. Они выполняют функции передаточного звена; => шестиполюсники, представляющие собой передаточные звенья с управляемым коэффициентом передачи.
Цепь с числом полюсов более двух принято называть многополюсником. В теории цепей многополюсники используются для составления топологических уравнений исследуемой цепи, например, уравнений по методу переменных состояния.
Схемы замещения. Для составления схемы замещения, или эквивалентной схемы, четырехполюсника с Y-параметрами воспользуемся его уравнениями , из которых следует, что входной и выходной токи содержат две составляющих, одна из которых создается напряжением Ux, другая — напряжением 02, при этом:
· составляющие токов YuUl , Y 22 U 2 можно рассматривать как отклики при воздействии входного и выходного напряжения на двухполюсники Уп, Y 2 2, подключенные соответственно к входным 1-1 и выходным 2-2 зажимам четырехполюсника;
· составляющие токов YnU 2 , Y 2 x Ux можно рассматривать как источники, управляемые со стороны выходных 2-2 и входных 1-1 зажимов соответственно.
На рис. 4,а приведена схема замещения Y-четырехполюсника, составленная в соответствии с изложенным выше принципом. На рис. 4,б,в,г приведены схемы G-, Н- и Z-четырехполюсников, а также описывающие их уравнения.

Пассивные элементы схем замещения отражают потери в четырехполюснике, а источники — возможность усиления мощности. При этом с помощью источника в выходной цепи моделируется полезный эффект усиления, а с помощью источника во входной цепи — паразитный эффект передачи мощности из выходной цепи, приводящей к возможному самовозбуждению четырехполюсника.
Тема №2: Электрические цепи синусоидального тока. Трехфазные цепи. [Электротехника Электронное пособие для тудентов очной и заочной форм обучения всех технических специальностей]
Получение синусоидальной электродвижущей силы (ЭДС). Способы представления синусоидальных ЭДС, напряжений и токов. Действующие значения синусоидальных величин. Электрические цепи с резистором, индуктивностью и емкостью. Мощности цепи синусоидального тока. Коэффициент мощности цепи. Резонансные явления в цепях синусоидального тока, условия возникновения, практическое значение. Комплексный метод расчёта линейных цепей переменного тока.
Переменным электрическим током называется ток, который с течением времени изменяет свое значение и направление.
В электрических сетях используется синусоидальный переменный ток, который возникает в цепи под действием синусоидальной ЭДС.
Переменный ток вырабатывается специальными генераторами, принцип действия которых основан на явлении электромагнитной индукции.
4.1 Параметры переменного тока.
Синусоидальная ЭДС, ток и напряжение характеризуется следующими параметрами:
- мгновенное значение (i,u,e) – значение синусоидальной величины в заданный момент времени.
- амплитуда (Im,Um,Em) – наибольшее из всех мгновенных значений.
- период Т – время в течении которого переменная величина проходит полный цикл колебания и возвращается к исходному значению (время одного колебания).
- частота – количество колебаний в единицу времени
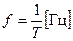
Промышленная частота в России равна 50 Гц.
- угловая частота (угловая скорость) – угол поворота рамки в магнитном поле в единицу времени.
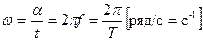
- начальная фаза – угол, определяющий значение синусоидальной величины в начальный момент времени (t=0)
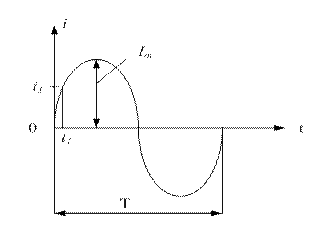
Разность начальных фаз двух синусоидальных величин определяет угол сдвига фаз этих величин.
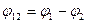
Любая переменная величина имеет свой закон изменения.
Например:
Ток 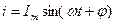
Напряжение 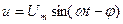
- действующее значение (Im,Um,Em) – это такое значение постоянного тока, который за время, равное периоду переменного тока на данном резисторе выделяет столько же тепла, сколько переменный ток за то же время.
Действующее и амплитудное значения связаны соотношением:
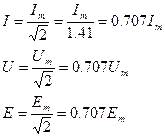
4.1.1. Временные и векторные диаграммы.
График зависимости переменной величины (i,u,e) от времени называется временной или волновой диаграммой.
Если переменная величина появляется раньше начала времени отсчета (начала координат), то она называется опережающей по фазе, угол 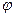 положительный (рис. 4.1.1 а). На графике она начинается левее начала координат.
положительный (рис. 4.1.1 а). На графике она начинается левее начала координат.
Если переменная величина появляется позже начала времени отсчета, она называется отстающей по фазе, угол 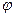 отрицательный. На графике она начинается правее начала координат (рис.4.1.1 б).
отрицательный. На графике она начинается правее начала координат (рис.4.1.1 б).
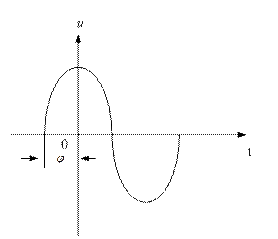
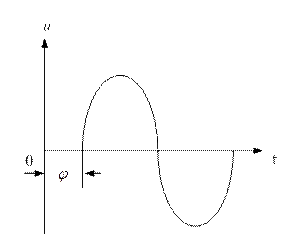
а) б)
Рисунок 4.1.1
Совокупность векторов, изображающих синусоидальные величины, называется векторной диаграммой.
Величина, опережающая по фазе, откладывается против часовой стрелки на заданный угол по отношению к горизонтальной оси.
Величина, отстающая по фазе, откладывается по часовой стрелке на заданный угол по отношению к горизонтальной оси.
Пример
Изобразить с помощью векторных диаграмм токи: 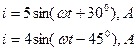
Выбирается масштаб тока 
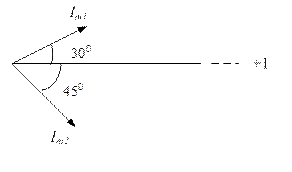
Выразим ток, напряжения, мощность и активного сопротивления в комплексной форме.
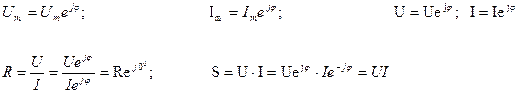
4.2. Расчет цепей переменного тока с различными элементами.
4.2.1. Цепь с активным сопротивлением (с резистором).

К зажимам цепи приложено синусоидальное напряжение
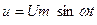
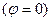
В любой момент ток в цепи определяется по закону Ома:
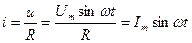
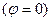
Ток и напряжение в любой момент времени совпадают по фазе.
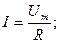
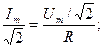
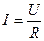
Таким образом, закон Ома справедлив для любых значений тока(мгновенных, амплитудных, действующих).
Мощность в любой момент времени:
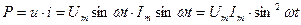
Временная (а) и векторная (б) диаграмма приведены на рисунке 4.2.1

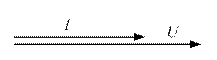
а) Временная диаграмма б) Векторная диаграмма
Выразим ток, напряжения, мощности и активного сопротивления в комплексной форме
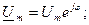
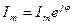 ;
; 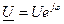 ;
; 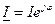
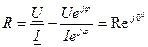 ;
; 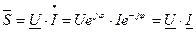 .
.
Пример:
К цепи переменного тока с активным сопротивлением R= 8 Ом приложено напряжение u = 45 sin( 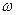 t+30°). Определить активную мощность цепи и уравнение мгновенного значения тока.
t+30°). Определить активную мощность цепи и уравнение мгновенного значения тока.
Решение:
1. Действующее значение напряжения 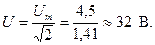
2. Действующий ток в цепи I= 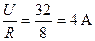
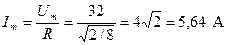 .
.
3. Мощность цепи P = U∙I = 32∙4 = 128 Вт.
4. Уравнение мгновенного значения тока i = 5,64 sin (  t+30°).
t+30°).
4.2.2. Цепь с индуктивностью
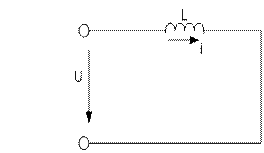
Рис. 4.2.3. а)
Если к указанной катушке приложить синусоидальное напряжение, то в цепи будет протекать синусоидальный ток, переменный магнитный поток которого индуцирует в катушке ЭДС самоиндукции:
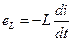
где 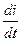 - скорость изменения тока;
- скорость изменения тока;
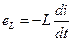 =
= 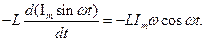
Напишем для цепи, изображенной на рис. 4.2.3. уравнение второго закона Кирхгофа.
Так как, R цепи равно нулю, то iR=0, поэтому u+ 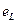 =0, откуда и u= -
=0, откуда и u= - 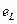 т.е.
т.е. 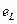 равна и противоположна по направлению напряжению на зажимах цепи. Подставив значение
равна и противоположна по направлению напряжению на зажимах цепи. Подставив значение 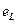 в эту формулу получим:
в эту формулу получим:
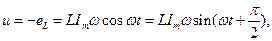
Из этой формулы видно, что напряжение на зажимах цепи опережает по фазе ток на угол 90° или ток отстает по фазе от напряжения на угол 90°. Амплитуда напряжения 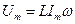 , откуда
, откуда 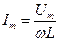 .
.
Разделив обе части последней формулы на 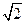 , получим выражение для действующего значения тока
, получим выражение для действующего значения тока 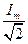 =
= 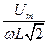 ; I=
; I= 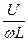 .
.
Выведенная формула есть выражение закона Ома для данной цепи, следовательно, 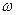 L представляет величину сопротивления этой цепи, называемого индуктивным сопротивлением и обозначаемого
L представляет величину сопротивления этой цепи, называемого индуктивным сопротивлением и обозначаемого 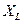

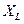 =
= 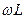 =
= 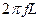
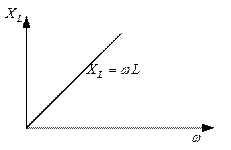 Рис. 4.2.3. б)
Рис. 4.2.3. б)
Из формулы следует, что индуктивное сопротивление цепи пропорционально индуктивности L и угловой частоте переменного тока.
Индуктивным сопротивлением называется величина, характеризующая противодействие ЭДС самоиндукции переменному току.
Выразим значения напряжения, тока и индуктивного сопротивления в комплексной форме.
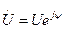 ;
; 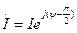 .
.
Комплекс индуктивного сопротивления найдется так:
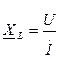 =
= 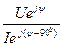 =
= 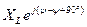 =
= 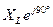 .
.
В алгебраической форме комплекс 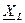 выразится так:
выразится так:
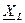 =
=  ,
,
Поскольку cos 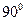 =0; sin
=0; sin 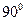 =1.
=1.
Мощность цепи
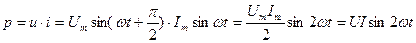 ;
;
Отсюда видно, что кривая мощности имеет синусоидальную форму и частоту, в 2 раза большую, чем частота тока, напряжения.
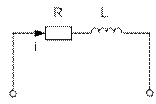
4.2.3. Цепь с индуктивностью и активным сопротивлением.
На практике используются реальные катушки индуктивности, которые обладают активным и индуктивным сопротивлением.
На схеме рис. 4.2.3.1 индуктивность и активное сопротивление отделены друг от друга и показан как участки цепи для удобства расчетов.
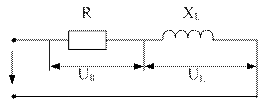
Рисунок 4.2.3.1
Допустим, что в цепи протекает синусоидальный ток
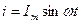
Решение
1. Индуктивное сопротивление катушки
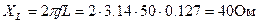
2. Полное сопротивление в комплексной форме
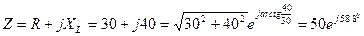
3. Ток в цепи

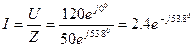
4. Амплитудное значение тока и напряжения
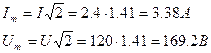
5. Напишем уравнение мгновенных значений тока и напряжения:
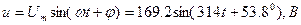

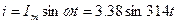
6. Комплекс мощности
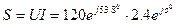 ВА.
ВА.
Вопросы для самоконтроля
1. Приведите свойства цепи с активным сопротивлением.
2. Свойства цепи с индуктивностью.
3. Запишите формулу полного сопротивления в символическом виде для цепи RL.
4. Запишите закон Ома для цепи с RL в комплексном виде.
Цепь с емкостью.
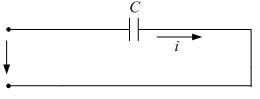
Ток в цепи с емкостью
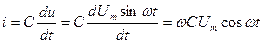
Выразим 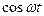 через
через 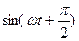 , получим
, получим
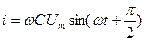
Т.е. ток опережает по фазе напряжения на 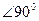 . Из выражения тока следует, что
. Из выражения тока следует, что 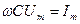 .
.
Это выражение можно написать в таком виде:
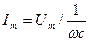 - что является выражением закона Ома для цепи с идеальной емкостью.
- что является выражением закона Ома для цепи с идеальной емкостью.
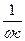 - выражает величину сопротивления, которое называется реактивным емкостным сопротивлением и обозначается ХС .
- выражает величину сопротивления, которое называется реактивным емкостным сопротивлением и обозначается ХС .
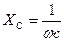
ХС - это величина, характеризующая противодействие, оказываемое напряжением на обкладках конденсатора переменному току.
В комплексной форме:
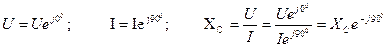
Для алгебраической формы:
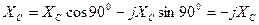
Зависимость ХС от частоты приведена на графике 4.2.4.1
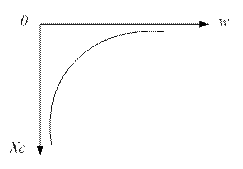
Рисунок 4.2.4.1
Векторная диаграмма цепи на рис. 4.2.4.2
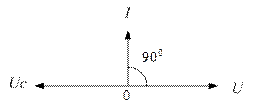
Рисунок 4.2.4.1
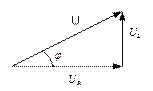
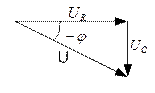
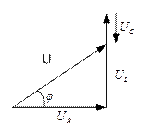
4.2.4. Цепь с активным сопротивлением и емкостью
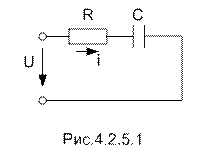
Если в цепи с последовательно соединенными R и С протекает синусоидальный ток 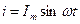 , то он создает падения напряжений на активном и емкостном сопротивлениях.
, то он создает падения напряжений на активном и емкостном сопротивлениях.
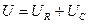
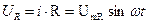
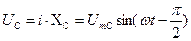
Напряжение цепи изменяется по синусоидальному закону и отстает по фазе от тока на угол 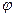 < 90°, т.е.
< 90°, т.е. 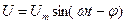
Построим векторную диаграмму (рис. 4.2.5.2) и по ней определим действующее значение напряжения.
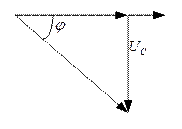
Рис. 4.2.5.2
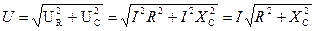
Откуда закон Ома для данной цепи:
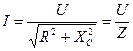
В символическом виде:
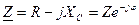
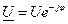 ;
; 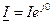 ;
; 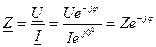
Полная мощность: 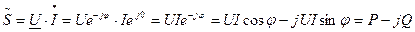
Пример:
R=8 Ом
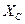 =6 Ом
=6 Ом
U=220В

Определить: I, 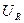 ,
, 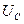 ,S
,S
Решение:
1. Полное сопротивление цепи:
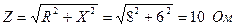
2. Ток в цепи:
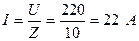
3. Напряжение на участках:
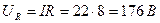
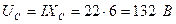
4. Полная мощность:
S=UI=220∙22=4840 ВА
Активная мощность:
Р=S cos 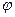 =4840∙0,8=3872 Вт
=4840∙0,8=3872 Вт
Реактивная мощность:
Q=S sin 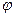 =4840∙0,6=2904 Вар
=4840∙0,6=2904 Вар
(sin 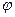 =
= 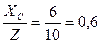 )
)
Вопросы для самоконтроля
1. Приведите векторную диаграмму напряжений для цепи RC.
2. Запишите формулу закона Ома в символическом виде для цепи RC.
3. Запишите закон изменения напряжения на емкости, если ток в цепи изменяется по закону: i= 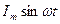 .
.
4. Рассчитайте полное сопротивление цепи в символическом виде, если R=12 Ом, С=253 мкФ, f=50 Гц.
4.2.5. Неразветвленная цепь с R,L,C
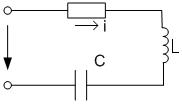
Рис. 4.2.6.1
Если в цепи, рис. 4.2.6.1 протекает синусоидальный ток, то он создает падение напряжений на всех элементах цепи. По второму закону Кирхгофа:
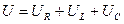
где 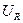 = i R =
= i R = 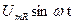
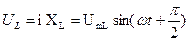
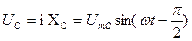
Так как, в рассматриваемой цепи имеется два реактивных сопротивления 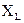 и
и 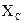 , то возможны три режима:
, то возможны три режима:
1) 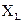 >
> 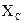 ; 2)
; 2) 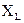 <
< 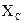 ; 3)
; 3) 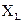 =
= 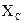
Векторная диаграмма для случая 1) изображена на рис. 4.2.6.2.
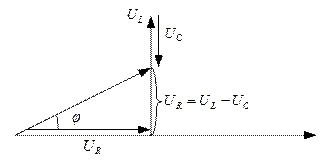
Рис. 4.2.6.2.
Знак перед углом  зависит от режима цепи.
зависит от режима цепи.
Если 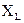 >
> 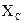 ,
, 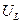 >
> 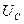 , цепь имеет индуктивный характер, угол
, цепь имеет индуктивный характер, угол 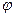 положительный.
положительный.
Если 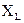 <
< 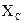 ,
, 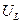 <
< 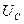 , цепь имеет емкостной характер, угол
, цепь имеет емкостной характер, угол 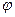 отрицательный.
отрицательный.
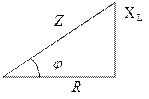
Закон Ома:
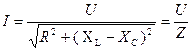
где Z = 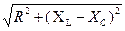 - полное сопротивление.
- полное сопротивление.
В комплексной форме: 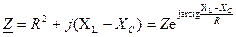
Треугольники сопротивлений и мощностей приведены на рисунке 4.2.6.3. (а и б)

а) б)
рис. 4.2.6.3.
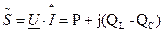 - полная мощность в комплексном виде.
- полная мощность в комплексном виде.
4.2.6. Колебательный контур
Основные параметры контура
Если предварительно зарядить конденсатор и подключить его к индуктивности (рис. 4.2.7.1), то будет происходить обмен энергией между электрическим полем конденсатора и магнитным полем катушки. В этой цепи будут происходить колебания, поэтому этот контур называется колебательным.
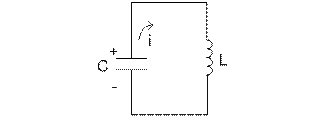
Рис.4.2.7.1.
Так как колебания происходят без воздействия внешнего источника, а за счет заранее занесенной энергии, то они называются свободными.
Колебания происходят с определенной частотой 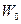 , называемой частотой свободных колебаний.
, называемой частотой свободных колебаний.
Из условия равенства энергий 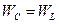
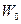 =
= 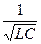 ;
; 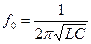 ;
;
Основными параметрами колебательного контура, кроме частоты свободных колебаний, являются:
- период свободных колебаний:
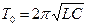 ;
;
- характеристическое (волновое) сопротивление:
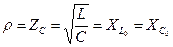
Характеристическим сопротивлением называется индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний.
Так как в контуре отсутствуют потери, то контур называется идеальным.
В реальном колебательном контуре (рис. 4.2.7.2) имеются потери, поэтому при возникновении в контуре свободных колебаний энергия предварительно заряженного конденсатора тратится безвозвратно, преобразуясь в тепло. В результате затраты энергии постепенно уменьшается её запас и амплитуда контура уменьшается до нуля. Следовательно, колебания в контуре будут затухающими.(рис 4.2.7.3)
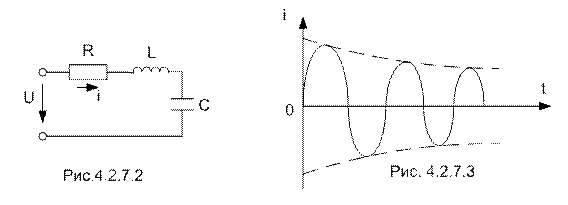
Для характеристики интенсивности затухания свободных колебаний введено понятие «затухание контура». Затуханием называется отношение активного сопротивления контура к его характеристическому сопротивлению.
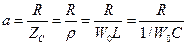
Величина, обратная затуханию, называется добротностью контура.
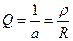
Добротность характеризует качество контура.
Рассмотрим различные варианты последовательного соединения элементов в цепях переменного тока.
| Схема | Треугольник напряжений | Треугольник сопротивлений | Треугольник мощностей |
| 
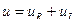 0<
0<  <90° <90°
| 
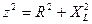
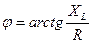
| 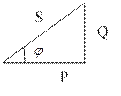
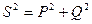
 =arctg =arctg 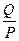
|
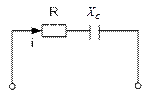
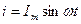
| 
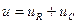 -90°<
-90°< 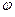 < 0 < 0
| 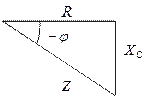
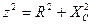
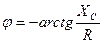
| 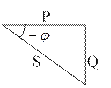
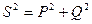
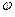 = - arctg = - arctg 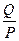
|
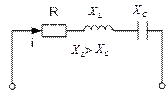
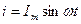
| 
| 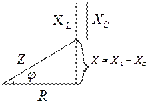 Цепь носит характер RL
Цепь носит характер RL
| 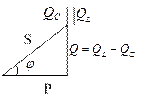
|
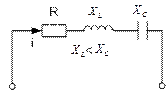
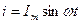
| 
| 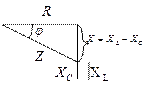 Цепь носит характер RC
Цепь носит характер RC
| 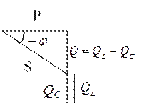
|
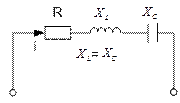
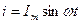
| 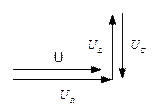
 =0 =0
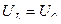 U=
U= 
| 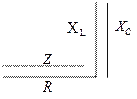 x = 0
Z = R
Цепь носит характер R
x = 0
Z = R
Цепь носит характер R
| 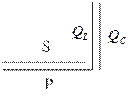
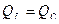 S = P
S = P
|
4.2.7.Гармонические колебания в цепи при параллельном соединении элементов R,L,C.
К цепи, содержащей параллельное соединение R,L,C
(рис. 4.2.8.1 а) приложено напряжение u= 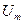 sin
sin 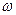 t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
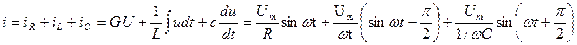 ,
,
где, 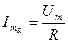 =G
=G 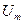 ,
,
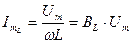 ,
,
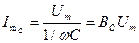 .
.
Полная проводимость цепи будет равна: 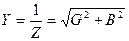
Активная проводимость: 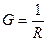
Реактивная проводимость: 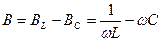
При параллельном соединении элементов строят треугольники токов и проводимостей (рис.4.2.8.1.б,в)
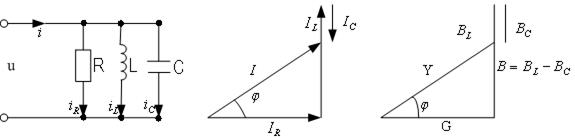
а) б) в)
Рис. 4.2.8.1.
4.2.8. Резонанс в электрических цепях переменного тока.
В радиотехнике и электросвязи большое значение имеет явление резонанса. Такое явление возникает в цепях, содержащих участки, с емкостным и индуктивным характером. Если цепь содержит последовательно соединенные с генератором элементы, то она называется последовательным колебательным контуром.(рис. 4.2.9.1а). Если элементы соединены параллельно с генератором, то цепь носит название – параллельный колебательный контур. (рис. 4.2.9.1б).
Среди многообразия частот имеется частота, на которой в цепи происходит обмен энергией между магнитными и электрическими полями. К генератору энергия не возвращается. От генератора поступает в контур столько энергии, сколько её тратится на активном сопротивлении цепи, тем самым обеспечиваются незатухающие колебания в контуре.
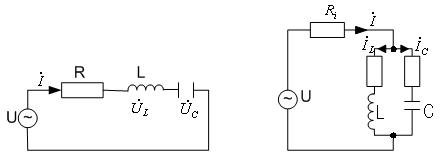
а) б)
рис. 4.2.9.1
· Частоту, на которой наблюдается явление резонанса, называют резонансной и определяют по формуле:
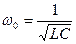 ;
; 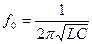
· Характеристическим сопротивлением контура называют реактивные сопротивления на резонансной частоте и определяют как:
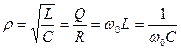 [Ом]
[Ом]
· Резонансные свойства контура характеризуются добротностью контура, которая равна:

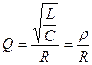
Добротность контура зависит от внутреннего сопротивления генератора 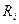 .
.
В последовательном колебательном контуре, (рис.4.2.9.1а) чем больше 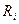 , тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
, тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
В параллельном колебательном контуре, (рис. 4.2.9.1б) если 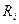 будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
Различают два типа резонансов. В последовательном колебательном контуре возникает резонанс напряжений, а в параллельном – резонанс токов. Свойства цепей при резонансе рассматриваются в следующей таблице:
Условия возникновения резонанса напряжений:
1. реактивные сопротивления контура равны.
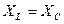 ; ; 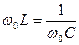 2. частота колебательного контура должна равняться частоте питающего сеть генератора
2. частота колебательного контура должна равняться частоте питающего сеть генератора 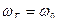
| Условия возникновения резонанса токов:
1. Реактивные проводимости параллельных ветвей равны.
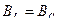 ; ; 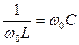 2. частота колебательного контура должна равняться частоте питающего сеть генератора
2. частота колебательного контура должна равняться частоте питающего сеть генератора 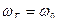
|
| Резонанс напряжений – это явление при котором напряжение на реактивных элементах в Q раз больше, чем напряжение питающего генератора. При этом ток в контуре максимальный | Резонанс токов - это явление при котором ток в параллельных ветвях в Q раз больше, чем ток в неразветвленной части цепи. При этом ток в контуре минимальный. |
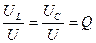 Векторная диаграмма напряжений
Векторная диаграмма напряжений

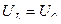
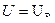 Резонансная кривая контура
Резонансная кривая контура
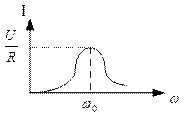
| 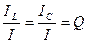 Векторная диаграмма токов
Векторная диаграмма токов
 Резонансная кривая контура
Резонансная кривая контура
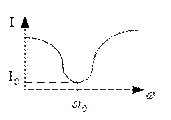
|
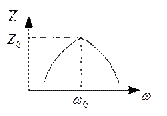
Входное сопротивление схемы при резонансе минимально и равно активному сопротивлении.
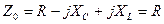
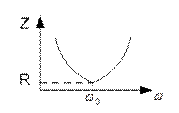
| Входное сопротивление схемы при резонансе максимально и равно.
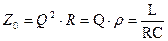
|
Важной характеристикой колебательного контура является полоса пропускания – это полоса частот, в пределах которой величина не меньше 0,707 от своего максимального значения. Полосу пропускания можно определить по формуле:
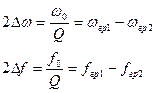
Где: 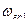 ;
; 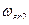 ;
; 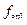 ;
; 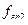 - граничные частоты, на которых величина равна 0,707 от своего максимального значения.
- граничные частоты, на которых величина равна 0,707 от своего максимального значения.
Колебательные контуры и явление резонанса широко используются в радиотехнике и электросвязи. В радиоприемниках и усилителях они являются избирательными цепями, в автогенераторах, электрических фильтрах, в корректорах и других устройствах являются частотно-зависимыми элементами.
Пример:
Электрическая цепь состоит из последовательно соединенных резистора R=15 Ом, катушки индуктивности L=636 мкГн и конденсатора C=600 пФ.
Определить резонансную частоту 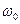 , характеристическое сопротивление
, характеристическое сопротивление 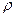 , добротностьQ, затухание d. Чему равны ток
, добротностьQ, затухание d. Чему равны ток 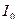 , расходуемая в цепи мощность
, расходуемая в цепи мощность 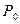 , напряжения на индуктивности
, напряжения на индуктивности 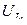 , и емкости
, и емкости 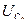 , если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на
, если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на 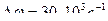 ?
?
Рассчитать и построить зависимости:
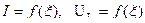
для значений обобщенной расстройки 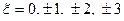 . Показать на графике полосу пропускания контура.
. Показать на графике полосу пропускания контура.
Решение:
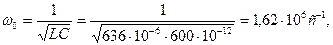
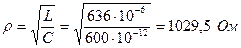 ,
,
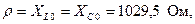
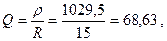
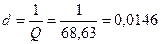 ,
,
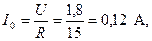
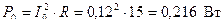 ,
,
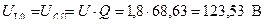 ,
,
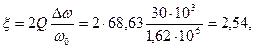
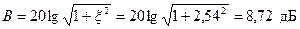 .
.
Рассчитаем и построим заданные зависимости:
1. 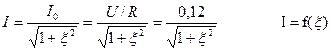


2. 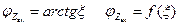

Вопросы для самоконтроля:
1. Что называется колебательным контуром?
2. Какие колебания называются свободными, вынужденными?
3. Что называется «резонансом напряжений»?
4. Что называется «резонансом токов»?
5. Условия возникновения резонансов
6. Что характеризует добротность контура?
7. Как определяется резонансная частота?
4.3. Расчет цепей символическим методом
Символический метод основан на использовании комплексных чисел.
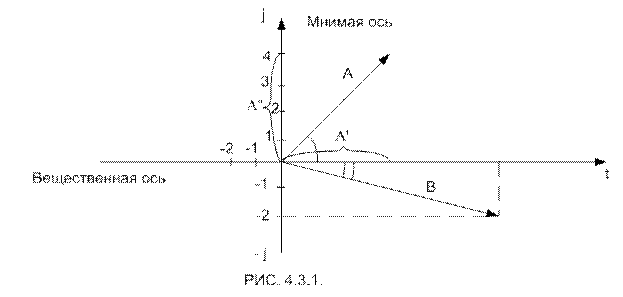
Комплексное число состоит из вещественной А' и мнимой А» частей. А = А' + jА».
Комплексное число можно представить вектором на комплексно-числовой плоскости. (рис. 4.3.1.) Проекция вектора на вещественную ось (ось абцисс) соответствует вещественной части комплексного числа А', проекция вектора на мнимую ось (ось ординат) соответствует коэффициенту при мнимой единице А»,
j-мнимая единица представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки.
Комплексным числам А=3+ j4 и В= 5-j2
Соответствуют векторы А и В, изображенные на рис. 4.3.1.
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Модуль комплексного числа:
|А|= 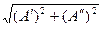 ;
;
Т.е. |А|= 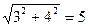 ;
; 
 |В|=
|В|= 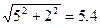
Углы 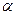 и
и 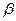 , образованные векторами А и В, называются аргументами комплексного числа
, образованные векторами А и В, называются аргументами комплексного числа
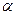 = arctg
= arctg 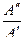
Для приведенных примеров
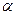 = arctg
= arctg 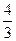 =53°10'
=53°10'
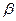 = arctg
= arctg 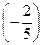 =-21°40'
=-21°40'
Существует 3 формы записи количественного числа:
1. Алгебраическая А = А' + jА»
2. Тригонометрическая А=|А|cos 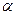 +j|А|sin
+j|А|sin 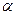 ,
,
Так как А'=|А| cos 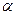
А»=|А| sin 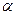
3. Показательная А=|А|е 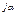 =5е
=5е 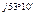
В=|В|е 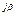 =5,4е
=5,4е 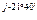
Для перевода из показательной формы в алгебраическую пользуются тригонометрической формой записи комплексного числа.
Для перевода из алгебраической в показательную форму определяют модуль и аргумент.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производят в алгебраической форме, а умножение и деление удобнее и проще производить в показательной форме.
При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:
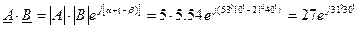
При делении комплексных чисел в показательной форме этих чисел делятся, а аргументы вычитаются
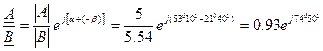
Если ток и напряжение изменяется по синусоидальному закону
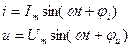
То их можно изобразить векторами и записать комплексными числами
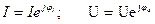
Комплекс полного сопротивления цепи:
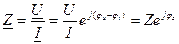
Алгебраическая форма записи комплекса полного сопротивления
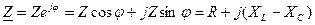
Любую цепь переменного тока можно рассчитывать по закону постоянного тока, если все величины представить в комплексной форме.
Комплекс полной мощности цепи 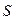 определяется произведением комплекса напряжения
определяется произведением комплекса напряжения 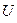 и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
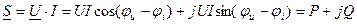
где Р- активная мощность
Q- реактивная мощность
Пример
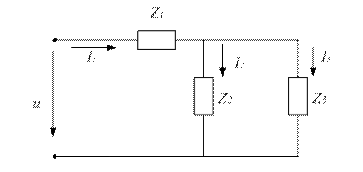
Определить полное сопротивление цепи (рис.4.3.2) напряжение на зажимах, мощности (активную, реактивную, полную) если
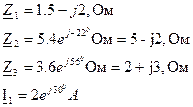
Решение
1. Полное сопротивление цепи
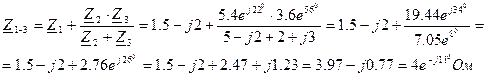
2. Напряжения на зажимах цепи
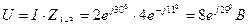
3. Полная мощность цепи
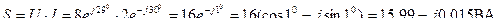
где Р=15.99 = 16 Вт – активная мощность
Q= -0.015 Вт – реактивная мощность
Вопросы для самоконтроля.
1 . Какие формы записи комплексных чисел вы знаете?
2. Сложите два числа
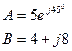
3. Перемножить два числа
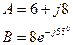
4. Выражаем токи через потенциалы, ЭДС и сопротивления.
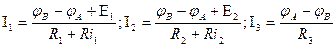 ,
,
5. Примем 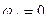
6. Подставляем полученные выражения токов в уравнение 1.

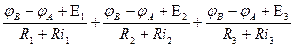
7. Подставим числовые значения и решаем полученное уравнение.
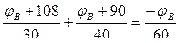
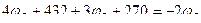
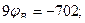
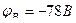
8. Определяем токи в ветвях.
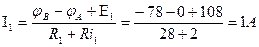
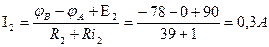
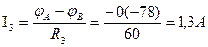
Действительные направления токов совпадают с выбранными.
Тема №3: Трехфазные цепи. [Электротехника Электронное пособие для студентов очной и заочной форм обучения всех технических специальностей]
Основными приемниками электрической энергии являются электрические двигатели, применяемые для приведения в движение рабочих машин. Наиболее простые из них трехфазные асинхронные двигатели. Для производства, распределения и передачи электрической энергии применяют трехфазные генераторы.
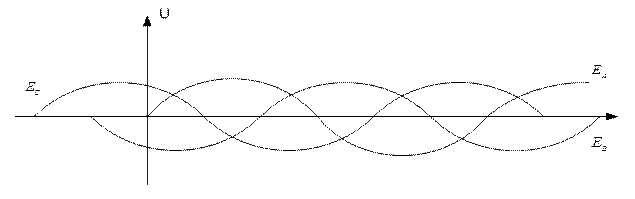
Система, состоящая из трех цепей, в которой действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые одним источником – называется трехфазной.
Система будет симметричной , если будут равны амплитуды фаз и углы сдвига фаз между каждой парой ЭДС.
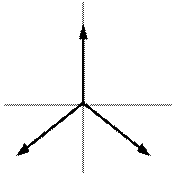
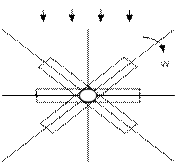
На рисунке 4.14а, изображены временные диаграммы ЭДС , на рисунке 4.14б, векторная диаграмма, а на 4.14в, иллюстрируется принцип получения трехфазной системы ЭДС . В равномерном магнитном поле с постоянной угловой скоростью  вращаются три одинаковых жёстко скрепленных друг с другом катушки.
вращаются три одинаковых жёстко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве относительно друг друга на 120°. В каждой катушке находится синусоидальная ЭДС одинаковой амплитуды. Уравнения ЭДС записывают в следующем виде:
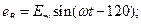
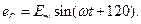

 а)
а)
ЕА
ЕС ЕВ
б) в)
Рисунок 5.11
Векторы вращающиеся против часовой стрелки и фазы чередуются А, В, С, что называют прямой последовательностью фаз.
Пример 5.1
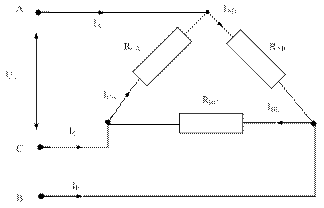
В цепь трехфазного тока с линейным напряжением Uл = 220 В включена треугольником нагрузка. Сопротивление фаз одинаковое RAB = RBC = RCA = 100 Ом. Определить фазное напряжение, линейный и фазный токи. Построить векторную диаграмму. Схема устройства изображена на рисунке 5.20 а.
а) б)
Рисунок 5.17
Так как, требуется рассчитать симметричную схему RAB = RBC = RCA, то решение сводится к расчету одной фазы.
1. При соединении фаз треугольником Uл = Uф = 220 В.
2. Фазные токи определяются по закону Ома 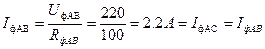
3. Линейные токи 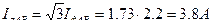
4. Потребляемая мощность 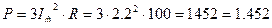 кВт
кВт
5. Построим векторную диаграмму. Так как, в трехфазной системе действуют три напряжения, сдвинутые на 1200, то пример UА =220 В, UВ = 220 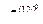 В,
В,
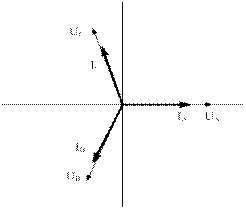
UС = 220 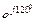 В. Нагрузка имеет резистивный характер, поэтому токи будут совпадать по фазе напряжением. Выберем масштаб по напряжению МU 100 В/см, по току МI 2 А/см (рисунок 5.17 б).
В. Нагрузка имеет резистивный характер, поэтому токи будут совпадать по фазе напряжением. Выберем масштаб по напряжению МU 100 В/см, по току МI 2 А/см (рисунок 5.17 б).
Пример 5.2
В трехфазную цепь с линейным напряжением (рис.5.18) 220В включен приемник, соединенный треугольник. Сопротивлением каждой фазы равно 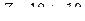 . Найти фазные и линейные токи.
. Найти фазные и линейные токи.
Решение:
1. Расчет проводится комплексным методом. Примем, что вектор напряжения UAB направлен по действительной оси, тогда: UAB = UA= 220B; UBC = UB = 220 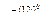 B;
B;
UCA = UC = 220 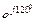 B.
B.
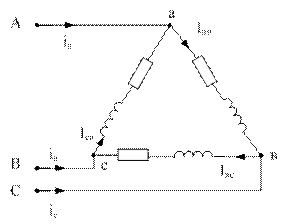
Рисунок 5.18
2. Определим фазные токи:
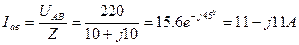
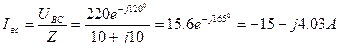
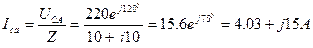
3. Составим уравнения для определения линейных токов (по 1 закону Кирхгофа) и определим:
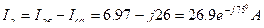
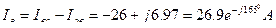
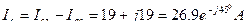
Вопросы для самоконтроля:
1. Какие цепи называются трехфазными?
2. Какие токи и напряжения называются линейными?
3. Какое соединение фаз называется звездой?
4. Для чего нужен нулевой провод?
5. Какое соединение фаз называется треугольником?
2 Модуль. Магнитные цепи и электромагнитные устройства – ПК-3:
Тема №1: Трансформаторы
Электромагнетизм
Тема посвящена рассмотрению основных законов электромагнитных явлений. Необходимо усвоить, что в пространстве, окружающем проводники с током, обнаруживаются особые явления, обусловленные наличием электромагнитного поля.
Магнитное поле
Магнитным полем называется одна из форм электромагнитного поля, возбуждаемая движущимися электрическими зарядами и характеризующаяся силовым воздействием на движущиеся заряженные частицы.
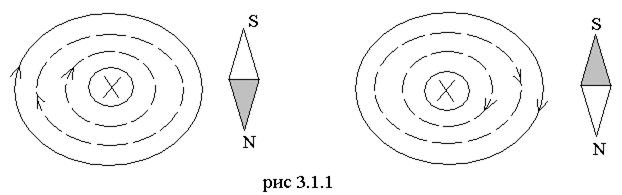
Направление магнитного поля связано с направлением тока. Графически магнитное поле изображается магнитными линиями, которые замкнуты и проводятся так, чтобы направление касательной в каждой точке линии совпадало с направлением поля.
Магнитное поле прямолинейного проводника с током имеет вид концентрических окружностей и направление его силовых линий определяется по «правилу буравчика», если ввинчивать буравчик в провод, то направление вращения его рукоятки будет совпадать с направлением магнитных силовых линий (рис. 3.1.1).
Параметры магнитного поля
Интенсивность магнитного поля характеризуется параметрами: напряженность, магнитная индукция, магнитный поток.
Напряженностью магнитного поля называется векторная величина, характеризующая интенсивность магнитного поля в данной его точке.
Напряженность в пространстве, окружающем проводник с током, вычисляется по формуле:
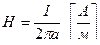
где: I – сила тока в проводнике, А
а - расстояние от оси провода до выбранной точки пространства вокруг проводника, м
Напряженность магнитного поля внутри катушки (соленоида) на ее оси, если длина катушки больше диаметра.
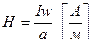
где: w - число витков катушки
С напряженностью связано понятие о намагничивающей силе.
Намагничивающей силой называется величина, характеризующая свойство тока возбуждать магнитное поле (Fm).
Для проводника с током Fm = I.
Так как, 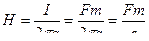 ,
,
то напряженность магнитного поля – это величина численно равная намагничивающей силе, приходящейся на единицу длины магнитной силовой линии радиуса а.
Векторная величина, характеризующая интенсивность магнитного поля с учетом влияния среды, называется магнитной индукцией.
Величина магнитной индукции определяется по формуле:
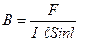 или
или 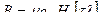
где: μа – абсолютная магнитная проницаемость среды, Гн/м
μа = μо 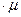
где: μо – магнитная проницаемость вакуума,
μо = 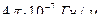
μ - относительная магнитная проницаемость среды;
F - сила, действующая на проводник с током.
Магнитная индукция в сердечнике катушки
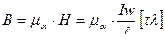
Произведение магнитной индукции В на площадь S поверхности, которую пересекает линии магнитного поля, называется магнитным потоком.
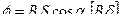
Н и В связаны соотношением 
 - угол между направлением вектора В и перпендикуляром к поверхности S.
- угол между направлением вектора В и перпендикуляром к поверхности S.
В сердечнике катушки 
Вопросы для самопроверки
1. Что называется электромагнитной индукцией?
2. Что называется самоиндукцией?
3. Как определяется ЭДС самоиндукции?
4. Что называется взаимоиндукцией?
5. От чего зависит коэффициент магнитной связи и в каких пределах Rн изменится?
6. Какое включение катушек называется согласованным, а какое – встречным?
Вопросы для самопроверки
1. Что называется трансформатором?
2. На чем основан принцип действия трансформатора?
3. Приведите схему однофазного трансформатора?
4. Что называется коэффициентом трансформации?
5. Какой трансформатор называется понижающим, а какой – повышающим?
6. Как определяется КПД трансформатора?
7. Из чего складываются потери трансформатора?
Тема №2: Электрические машины [Яцкевич]
Устройство и принцип действия машин постоянного тока.
Машина постоянного тока состоит из двух основных частей: подвижной и неподвижной. Неподвижная часть — индуктор представляет собой электромагнит, имеющий одну или несколько пар полюсов. Он состоит из станины, полюсов и обмоток возбуждения, расположенных на полюсах. Под действием постоянного тока, протекающего по обмоткам возбуждения, полюса намагничиваются. Таким образом, создается магнитный поток машины.
Вращающаяся часть машины - якорь состоит из вала, сердечника и обмотки якоря, соединенной с коллектором. Якорная обмотка через коллекторные пластины и прилегающие к ним контактные щетки соединяется с внешней электрической цепью.
Когда якорь генератора вращается каким-либо двигателем, в обмотке якоря, пересекающей магнитный поток полюсов, индуктируется э.д.с. Начальный ток возбуждения в параллельной обмотке возникает под действием небольшой э.д.с., которая индуктируется за счет остаточного магнитного потока, после чего происходит «самовозбуждение» генератора.
У генератора смешанного возбуждения на полюсах размещаются две обмотки возбуждения: параллельная ( шунтовая ), включаемая в цепь параллельно якорю, и последовательная (сериесная), включаемая последовательно с обмоткой якоря (рис. 1 ).
На клеммном щитке такого генератора имеются три пары клемм, принадлежащие якорной цепи (Я1 и Я2), параллельной обмотке (Ш1 и Ш2) и последовательной обмотке (С1 и С2).
Если маркировка клемм на щитке отсутствует, то отыскать клеммы одной или другой обмотки можно при помощи электрической лампы и источника тока, при этом нужно иметь ввиду, что клеммы якорной цепи Я2 и Д1
через щетки соединены с коллектором.
Параллельная обмотка в отличие от последовательной обмотки возбуждения имеет большое количество витков, изготовлена из тонкого провода и поэтому имеет бòльшее сопротивление.
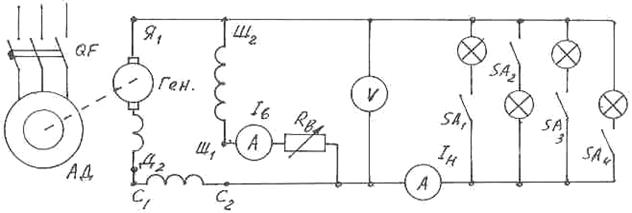
Рис. 1. Схема генератора со смешанным возбуждением
Величина э. д. с, индуктируемая в якорной обмотке, прямо пропорциональна магнитному потоку Ф и скорости вращения якоря п:
Е = СеФп. ( 1 )
Коэффициентом пропорциональности СЕ является постоянная для данной машины величина, зависящая от числа пар полюсов р, числа пар параллельных ветвей а и числа проводников якорной обмотки N:
Се= рN / 60а. ( 2 )
При работе генератора якорь его обычно вращается с постоянной скоростью. Поэтому э.д.с. генератора регулируют за счет величины магнитного потока (уравнение 1), изменяя ток в параллельной обмотке возбуждения.
Зависимость э.д.с. от тока возбуждения выражается характеристикой холостого хода, которая снимается опытным путем при отсутствии нагрузки и при постоянной скорости вращения якоря. При холостом ходе последовательная обмотка возбуждения никакого влияния на работу генератора не оказывает, так как ток в этой обмотке отсутствует.
Намагничивающая сила IW последовательной обмотки возбуждения прямо пропорциональна току нагрузки генератора. Поэтому при увеличении тока нагрузки магнитный поток и э. д. с. генератора возрастают.
В результате этого напряжение на зажимах генератора смешанного возбуждения (уравнение 3) при увеличении тока нагрузки не уменьшается (как это имеет место у генератора параллельного возбуждения), а сохраняется примерно постоянным.
U = Е - Iя ( Rя + Rс ), ( 3 )
где Rя -сопротивление якоря, Rс - сопротивление последовательной обмотки.
При встречном включении последовательной обмотки э. д. с. генератора с ростом тока нагрузки уменьшается, т.к. в этом случае последовательная обмотка будет размагничивать полюсы генератора и уменьшать магнитный поток. Такой способ включения последовательной обмотки применяется только в генераторах специального назначения.
Внешняя характеристика генератора, выражающая зависимость напряжения от тока нагрузки, строится на основании опытов, проводимых при постоянной скорости вращения и неизменном сопротивлении в цепи параллельной обмотки возбуждения.
Режимы генератора, двигателя и электромагнитного тормоза. Способы возбуждения.
Работа двигателя постоянного тока основана на взаимодействии тока, протекающего по обмотке якоря, с магнитным полем индуктора. Ток в якорную обмотку из сети поступает через щетки и коллектор. Магнитное поле в двигателе создается при помощи обмотки возбуждения, расположенной на полюсах индуктора. У двигателя параллельного возбуждения эта обмотка включается параллельно якорной обмотке.
Частота вращения якоря двигателя постоянного тока зависит от приложенного напряжения U, тока якоря Iя и его сопротивления Rя , а также от магнитного потока Ф и конструктивной постоянной СЕ:
п = (U – Iя Rя ) / СЕФ , ( мин -1) . ( 1 )
Напряжение в сети обычно сохраняется постоянным и только при необходимости регулирования п в широком диапазоне применяют систему генератор - двигатель (Г-Д). Чаше частоту вращения якоря двигателя параллельного возбуждения регулируют изменением Ф или Iя . С этой целью в цепь обмотки возбуждения включают регулировочный реостат Rвозб (рис.1), при помощи которого можно изменять величину тока возбуждения Iвозб и магнитный поток Ф. Ток якоря можно регулировать введением реостата в цепь якоря, но при этом потери энергии, выделяемой в реостате пропорционально Iя 2Rp , будут значительно больше, чем при регулировании п током возбуждения.
Из формулы (1) видно, что Iвозб и Ф двигателя параллельного возбуждения не зависит от тока якоря. При постоянном Ф изменение будет обусловлено
только изменением падения напряжения в якорной цепи, обладающей небольшим сопротивлением Rя . Поэтому при увеличении нагрузки на валу и соответствующем нарастании тока якоря частота вращения снижается незначительно, т. е. данный двигатель обладает жесткой механической характеристикой.
Ток якоря при работе двигателя равен отношению
Iя = ( U – Е ) / Rя , ( 2 )
где Е – противо - э. д. с. двигателя.
В момент пуска, когда якорь двигателя еще не вращается, э.д.с. его равна нулю. В это время по якорю протекает наибольший, так называемый пусковой ток, который согласно уравнению (2) равен
Iпуск = U / ( Rя + Rnvcк ), ( 3 )
где Rnvcк - сопротивление пускового реостата, включаемого на время пуска последовательно с якорем (рис.1).
Вращающий момент двигателя постоянного тока пропорционален току якоря и магнитному потоку:
М = См Iя Ф, ( 4 )
где См - коэффициент, зависящий от количества полюсов и параметров якорной обмотки.
Для ускорения процесса пуска двигателя необходимо увеличить его крутящий момент путем увеличения магнитного потока. С этой целью перед пуском двигателя сопротивление регулировочного реостата уменьшают до нуля. В этом случае ток возбуждения ограничивается только сопротивлением самой обмотки возбуждения.
Момент сопротивления на валу при испытании двигателя в данной работе создается при помощи тормозного устройства в виде генератора постоянного тока. Момент на валу машины определяется по мощности генератора
P2 ≈ 1,1 · UГ ·IГ ; ( Вт ) ( 5 )
М = 9,55 P2 / п2 , ( Нм) ( 6 )
Мощность, потребляемая двигателем из сети, вычисляется как произведение Р1 = Uс I (Вт). ( 7 )
Коэффициент полезного действия двигателя
η = Р2 : Р1 . ( 8 )
Механические свойства двигателя характеризуются так называемым процентным изменением частоты вращения
∆n = 100% ( по – п ) / по , ( 9 )
где по - частота вращения якоря при холостом ходе,
п - частота вращения якоря при нагрузке двигателя.
Как уже упоминалось выше, двигатель параллельного возбуждения имеет жесткую механическую характеристику, и, следовательно, в отличие от других типов двигателей постоянного тока работает с небольшим процентным изменением частоты вращения.
Яцкевич В.В Электротехника с 139…146 , 150…155
Энергетические и электромагнитные процессы в генераторе и в двигателе постоянного тока, основные характеристики.
Яцкевич В.В Электротехника с 146…150
Устройство и принцип действия, основные свойства трёхфазного асинхронного двигателя. Механические и рабочие характеристики.
Яцкевич В.В Электротехника 103…125
Устройство, принцип работы и свойства трёхфазного синхронного генератора и двигателя. Яцкевич В.В Электротехника 125…139
Регистры
Классификация регистров
Регистр – функциональный узел объединяющий несколько однотипных триггеров.
Типы регистров:
1) Регистры защелки – строятся на триггерах защелках (К155ТМ5; К155ТМ7), запись в которые ведется уровнем стробирующего сигнала.
В триггере К155ТМ8 - запись ведется положительным фронтом стробирующего сигнала.
2) Сдвигающие регистры – выполняют функцию только последовательного приема кода.
3) Универсальные регистры – могут принимать информацию в параллельном и последовательном коде.
4) Специальные регистры – К589ИР12 имеют дополнительные варианты использования.
Сдвигающий регистр
Это регистр, содержимое которого при подаче управляющего сигнала может сдвигаться в сторону старших или младших разрядов. Например, сдвиг влево приведен в таблице 9.
| 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
Таблица 9 Сдвиг кода влево
Универсальные регистры
Счетчики
Классификация счетчиков
Функциональный узел предназначенный для счета импульсов называется счетчиком. По мере поступления входных импульсов счетчик последовательно перебирает свои состояния в определенном для данной схемы порядке. Например:

Длина списка используемых состояний К называется модулем пересчета или емкостью счетчика. Наиболее часто используются двоичные счетчики, у которых порядок смены состояний триггеров соответствует последовательности двоичных кодов. Применяются и другие виды кодирования,например sодинарное, когда состояние счетчика определяется местоположением движущейся единицы.
 К=3
К=3
Обычный счетчик перебирает свои состояния в возрастающем порядке (суммирующий счетчик), если наоборот, то это вычитающий счетчик. Если можно менять направление перебора - реверсивный счетчик. Если для переключения нужен синхросигнал, счетчик называется синхронным, если только входной сигнал, то асинхронным.
Рис.8-1 Схемное обозначение счетчика
CR – выход переноса {глава 4.1}, который используется для соединения со следующим счетчиком.
Интегральные микросхемы.
Базовые логические элементы
Разработкой каждой серии цифровых ИС начинается с базового логического элемента. Так называют элемент, который лежит в основе всех микросхем серии: комбинационных(логических), триггеров, счетчиков и др. Как правило, базовые логические элементы выполняют операции «И-НЕ» либо «ИЛИ-НЕ». Принцип построения базового элемента, способ управления его работой, напряжение питания и другие параметры являются определяющими для всех ИС данной серии. Широко распространены ИС, построенные на базовых элементах транзисторно-транзисторной логики (ТТЛ)
Технология ТТЛ
Базовый элемент ТТЛ (рис. 2-6) строится на основе многоэмиттерного транзистора {модуль 1 глава 1.5.1} VT1, обеспечивающего коньюнкцию входных сигналов Xi, и сложного инвертора на транзисторах VT2-:VT4, выполняющего операцию «НЕ».
Когда на все входы Xi многоэмиттерного транзистора поданы сигналы 1 (высокий потенциал, сравнимый с +E), все его эмиттерные переходы закрыты. Ток от источника через резистор R1 и коллекторный переход VT1 поступает на базу VT2. Транзистор VT2 открывается до насыщения и открывает VT4 также до насыщения. Транзистор VT3 в это время закрыт, поскольку напряжение на коллекторе открытого транзистора VT2 мало. Диод VD служит для повышения порога открывания транзистора VT3.
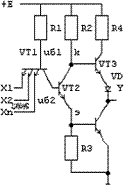
Рис.2-6 Базовый элемент ТТЛ
Таким образом, рассмотренный элемент ТТЛ выполняет логическую операцию «И-НЕ» ( 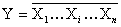 ).
).
Для ограничения тока через открытый транзистор VT3 при случайном коротком замыкании выхода элемента включен резистор R4.
В состав некоторых серий цифровых ИС ТТЛ входят логические элементы без коллекторной нагрузки выходного транзистора VT4 - элементы с «открытым» коллектором. Они предназначены для работы с внешней нагрузкой в виде индикаторных приборов, светодиодов и т.д.
Если какие либо из входов многоэмиттерного транзистора никуда не подключены, то это воспринимается элементом как подача на эти входы 1, так как тока в цепи неподключенного эмиттера нет. Поэтому, например, элементы «И-НЕ» («ИЛИ-НЕ») можно использовать как простые инверторы, подавая инвертируемый сигнал на один из входов «И-НЕ» или же соединяя все входы вместе. В схеме «И-НЕ» сигнал можно подавать только на один из входов, оставляя остальные неподключенными (рис.2-7).
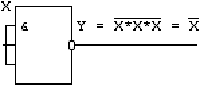
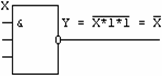
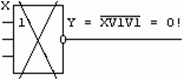
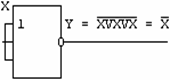
Рис.2-7 Использование элементов «и-не’,’или-не’ как инверторов
При подаче хотя бы на один из эмиттеров уровня «0», ток из выходной цепи Rн переключается во входную цепь и на выходе устанавливается «0». Если на все входы подать уровень «1», тогда во входной цепи тока не будет, он пойдет через Rн и на выходе будет «1». Данная схема выполняет операцию «и». Если на входы ничего не подавать, то тока во входной цепи также не будет и на выходе появится «висячая 1». При соединении многоэмиттерного транзистора и сложного инвертора образуется элемент «И-НЕ».
Технология КМОП
В качестве инверторов можно использовать МОП транзисторы, но р- и n-канальные цифровые элементы оказались непрактичными как базовые для массовых микросхем прежде всего из-за низкого быстродействия. Действительно, при Rс=100кОм и емкости нагрузки Сн=30 пФ время отключения составит t = 2,2RcCн= 6,6 мкс, что соответствует максимальной частоте входных импульсов 150 кГц.
Увеличить быстродействие на порядок позволяет последовательное (столбиком) соединение р и n-канальных МОП-транзисторов. Тогда резистор Rc в схеме не нужен, а заряд и разряд паразитных нагрузочных емкостей будет происходить через относительно небольшие сопротивления р- и n-каналов.
С помощью металлизации поверхности кристалла элементы структуры соединяются в схему инвертора DD1 (рис.2-11). К затворам присоединен защитный стабилитрон VD1, без него вход инвертора будет пробит статическим электричеством.
Цифровые микросхемы должны быть крайне устойчивы к таким явлениям, как пробои от статического или наведенного от силовых сетей электричества. Прежде всего защита гарантируется их структурой. На рис. 2-11 показана полная эквивалентная схема инвертора КМОП. Стоковое напряжение (плюс источника питания) подключается на n-подложку.
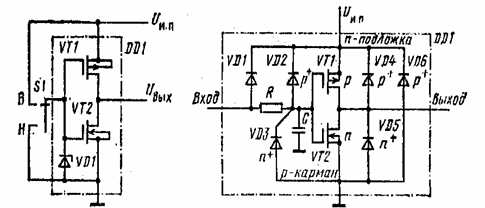
Рис.2-11 Упрощенная и полная схемы инвертора на КМОП транзисторах
Конденсатор С символизирует входную емкость инвертора. Как правило, она составляет от 5 до 15 пф. Диоды VD1 – VD3 защищают изоляцию затвора от пробоя. Диод VD1 имеет пробивное напряжение 25 В, VD2 и VDЗ-50 В. Последовательный резистор R=200 Ом... 2 кОм не позволяет скачку тока короткого замыкания передаваться в незаряженную входную емкость С. Тем самым защищается выход предыдущего (управляющего) инвертора от импульсной перегрузки. Диоды VD4-VD5 защищают выход инвертора от пробоя между n+ и p+ областями. Диод VD6 защищает канал от ошибочной перемены полярности питания.
ЭСЛ технология
Цифровые микросхемы эмиттерно-связанной логики (ЭСЛ) имеют наибольшее быстродействие, достигшее в настоящее время субнаносекундного диапазона. Особенность ЭСЛ в том, что схема логического элемента строится на основе интегрального дифференциального усилителя (ДУ), транзисторы которого могут переключать ток и при этом никогда не попадают в режим насыщения. Поэтому такие схемы самые быстродействующие.
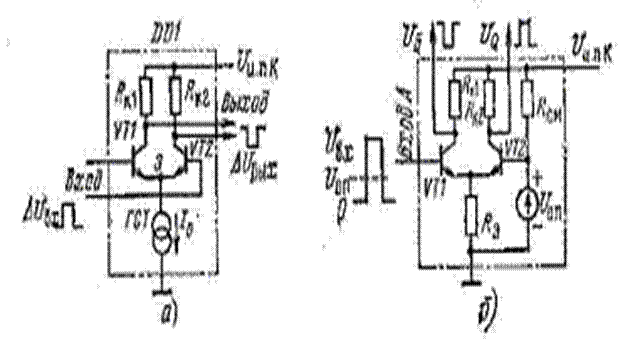
Рис.2-12 Схема элемента ЭСЛ
На рис.2-12а показана основа логического элемента DD1 - переключатель тока I0. Если входным сигналом Uвх открыть транзистор VТ1, через него потечет весь ток I0, вытекающий из общей точки связанных эмиттеров Э. На коллекторе транзистора VТ1 окажется напряжение низкого уровня. В этот момент транзистор VТ2 тока не имеет, он вынужденно находится в состоянии отсечки. На его коллекторе присутствует напряжение высокого уровня.
В отличие от аналоговых применений дифференциального усилителя, когда стремятся использовать разность напряжений Uвых между коллекторами, цифровая микросхема, переключающая ток I0, снабжается двумя инверсными выходами логических уровней, где выделяются напряжения высокого и низкого уровней.
На рис. 2-12б показан простейший одновходовый элемент ЭСЛ. Новым в развитии элемента DD1 (рис. 2-12а) здесь является источник опорного напряжения Uоп. Это напряжение фиксирует порог срабатывания переключателя тока. Тем самым дифференциальный усилитель превращается в логический элемент. У него теперь два состояния выходов, которые переключаются лишь при условиях: Uвх>Uоп или Uвх<Uоп. Однако при проектировании ЭСЛ ставилась задача: получить сверхскоростную логику. В схеме (рис.2-12б) этого достичь нельзя, так как выходное сопротивление выходов Q и Q велико, оно приближается к величине Rн. Для снижения выходного сопротивления к коллекторным выходам подключаются эмиттерные повторители, работающие в линейном режиме. Теперь выходное сопротивление эмиттерного выхода значительно уменьшается:
Rвых=Rk/(B+1), где (В+1) - коэффициент усиления по току транзистора-эмиттерного повторителя. Эмиттерные выходы чаще делаются «открытыми», чтобы можно было их соединять в элементы «монтажное ИЛИ». Сопротивление внешнего нагрузочного резистора Rэн можно выбрать от 300 Ом до 30 кОм.
Принципиальная особенность микросхем ЭСЛ: они питаются отрицательным напряжением -Uи.п.э (то есть напряжение подается от эмиттеров), а коллекторные цепи заземляются. Этим способом повышается помехоустойчивость ЭСЛ. Ток потребления Iпот вытекает из микросхемы в источник.
АЦП и ЦАП
ЦАП c матрицей R-2nR
1) Преобразование код → ток производится с помощью резистивной матрицы.
Переключатели Пi выполнены в виде транзисторных ключей:
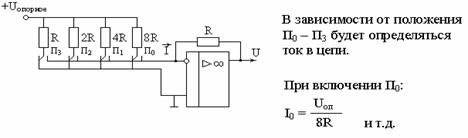
Рис.10-1 Резистивная матрица R-2nR
2) Преобразование ток → напряжение производится операционным усилителем. Величина выходного напряжения определяется резистором R, который установлен внутри корпуса ЦАП; ОУ подключается дополнительно.
ЦАП с матрицей R-2R
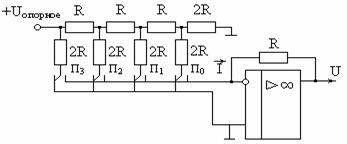
Рис.10-2 ЦАП с матрицей R-2R
Интегрирование.
АЦП последовательного счета
Структура такого АЦП показана на рис.10-4.
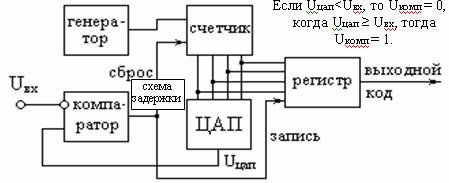
Рис.11-1 АЦП последовательного счета
На выходе счетчика появляется нарастающий код, который ЦАПом преобразуется в нарастающее напряжение Uцап. В тот момент, когда Uцап = Uвх, компаратор выдает сигнал равный «1», по которому полученный код записывается в регистр, и (с некоторой задержкой) сбрасывается счетчик. Процесс повторяется непрерывно.
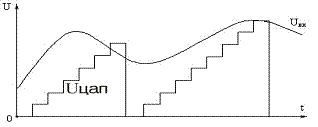
Рис.11-2 Процесс преобразования в АЦП
Недостаток: время преобразования пропорционально величине сигнала Uвх, поэтому отслеживать можно только сравнительно медленные сигналы.
Следяший АЦП
Модуль. Магнитные цепи и электромагнитные устройства – ПК-3:
Тема №1: Трансформаторы 59
Тема №2: Электрические машины [Яцкевич] 66
3. Модуль. Электроника – ПК-3
Тема №1: Электронные приборы [Джонс] 79
Тема №2: Электронные устройства. 104
Дата: 2018-12-28, просмотров: 459.