а) Прямая геодезическая задача
Рис. 3.5. Прямая геодезическая задача
Дано: координаты точки 1 х1, у1; горизонтальное проложение линии 1 – 2: d1,2;
дирекционный угол линии 1 – 2: a1,2 (рис.3.5).
Найти: координаты точки 2: х2, у2.
Решение: координаты точки 2: х2 = х1 + Dх; у2 = у1 + Dу, (3.6)
где приращения координат Dх = d · cos a; Dу = d · sin a, (3.7)
откуда х2 = х1 + d · cos a; у2 = у1 + d · sin a. (3.8)
Знаки приращений координат Dх и Dу зависят от знаков функций sin a и cos a.
б) Обратная геодезическая задача
 |
Рис. 3.6. Обратная геодезическая задача
Дано: координаты точек 1 и 2: х1, у1; х2, у2 (рис.3.6).
Найти: горизонтальное проложение линии 1 – 2: d1,2; дирекционный угол линии 1 – 2: a1,2.
Решение: Dх = х2 – х1; Dу = у2 – у1; (3.9)
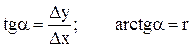; (3.10)
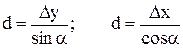. (3.11)
По значению tg a определяется румб линии. По знакам приращений координат определяется четверть, а по четверти определяется дирекционный угол линии.
Рис. 3.7. Знаки приращений координат
в зависимости от четверти
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.
Тема 4. Масштабы. Сведения из теории погрешностей
Масштабы
Масштаб – отношение длины линии на плане к соответствующей проекции этой линии на местности.
а) Численный масштаб – число, правильная дробь, в числителе – единица, знаменатель – степень уменьшения изображения.
Пример: Масштаб 1:1 000 – 1 сантиметру карты (плана) соответствует 1 000 сантиметров на местности или 10 метров. Масштаб 1:100 000 – 1 см карты соответствует 100 000 см местности или 1 000 м.
б) Линейный масштаб – графический чертеж (рис.4.1). Расстояние между большими отрезками постоянное и называется основанием масштаба. Обычно выбирают основанием отрезок в 2 см.
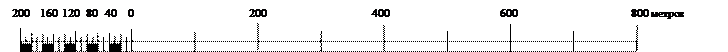
Масштаб 1: 10 000
Рис. 4.1. Линейный масштаб
Для масштаба 1: 10 000: в 1 см 100 м, в 2 см 200 м.
Левая часть делится на 10 частей, каждая часть делится еще пополам. Для данного масштаба одно маленькое деление соответствует 10 метрам.
Для определения расстояний по карте (плане) циркулем переносят на линейный масштаб (рис. 4.2) расстояние и оценивают его.
Пример: 400 + 90 = 490 м
Рис. 4.2. Пример определения расстояния по карте
в) Поперечный масштаб – применяют для более точного определения длин отрезков
 |
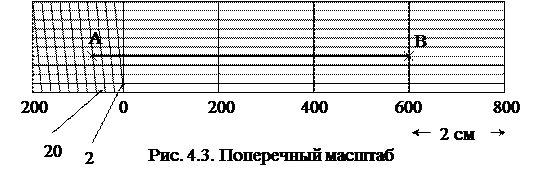
Рис. 4.4. Принцип определения наименьшего деления поперечного масштаба
На прямой линии (рис.4.3) откладывают отрезки по 2 см (основание масштаба). Вверх по перпендикуляру откладывают на равном расстоянии 10 равных частей. Левая часть полученного прямоугольника делится 10 наклонными линиями (трансверсалями). Наименьшее деление поперечного масштаба (рис.4.4) равен 1/10 части левой шкалы.
Пример 1: для масштаба 1:10 000, в 1 см 100 м, в 2 см 200 м. Одно деление слева от 0 - 20 м, одно деление при подъеме вверх по трансверсали - 2 м.
Расстояние АВ: по 200 м – 3 деления, по 20 м – 3 деления, по 2 м – 4 деления. Итого: 600 м + 60 м + 8 м = 668 м.
Пример 2: для масштаба 1:25 000, в 1 см 250 м, в 2 см 500 м. Одно деление слева от 0 - 50 м, одно деление при подъеме вверх по трансверсали - 5 м.
Расстояние АВ: по 500 м – 3 деления, по 50 м – 3 деления, по 5 м – 4 деления. Итого: 1500 м + 150 м + 20 м = 1670 м.
Наименьшее расстояние, различаемое глазом, 0,1 мм. Точностью масштаба называют горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм плана. Так для масштаба 1:5 000 в 1 см – 50 м, в 1 мм – 5 м, в 0,1 мм – 0,5 м. Для 1:5 000 точность масштаба 0,5 м.
Предельная точность масштаба 0,2 мм (точность, различаемая глазом 0,1 мм, и точность применяемых измерительных приборов 0,1 мм), т.е. для масштаба
1:5 000 это 1 м.
Дата: 2018-12-28, просмотров: 442.
