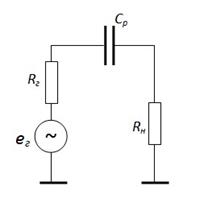
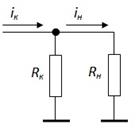
1) Разделительные конденсаторы. Любой C р отделяет источник сигнала (им может быть как e г - R г, так и выход очередного каскада) от нагрузки (ею может быть как ???, так и вход очередного каскада). Поэтому влияние C р на АЧХ можно выяснить с помощью следующей простой схемы.
АЧХ такой схемы есть зависимость модуля коэффициента передачи напряжения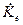 
от частоты ω.
;
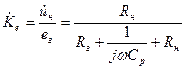Делим числитель и знаменатель на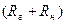 
. Получаем:
,
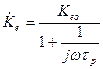где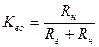 
- коэффициент передачи напряжения на C р (на частотах, где 
).
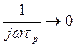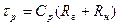- постоянная времени перезаряда C р.
Выражение для АЧХ:
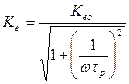. Ke уменьшается при уменьшении частоты.
Следовательно, C р учитывается только на НЧ. При этом легко найти ωн:
,
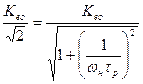откуда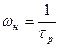 
, то есть ωн зависит не только от C р, но и от её постоянной времени.
; 
; 
.
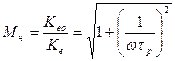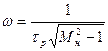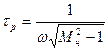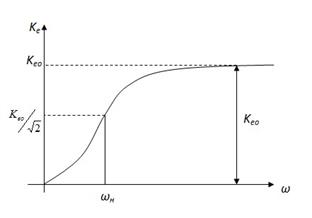
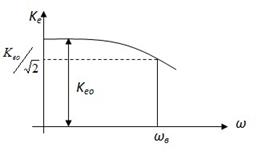
2) Конденсатор C э в эмиттерной цепи. Он предназначен для устранения отрицательной обратной связи, что и осуществляется на всех частотах, где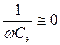 
. С уменьшением частоты 
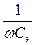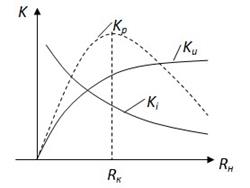
растёт, увеличивается степень обратной связи и Ke уменьшается, причём при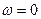 
Ke уменьшается не до нуля (см. рисунок).
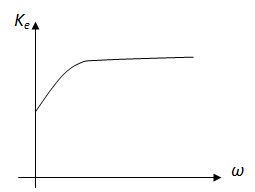Итак, C э учитывается только на НЧ.
3) Ёмкости C н,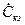 
, частотная зависимость 
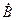. Прежде всего сделаем следующие замечания:
а) Частотная зависимость коэффициента 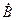есть следствие влияния диффузионной ёмкости эмиттерного перехода C диф э (см. параграф, посвящённый получению Т-образной эквивалентной схемы). То есть можно учитывать или C диф э (тогда B не зависит от частоты), или зависимость 
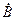от частоты (тогда не учитывать C диф э).
б) Любую из ёмкостей C н, 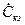и C диф э можно рассматривать как ёмкость, шунтирующую нагрузку. C н непосредственно шунтирует R н; 
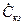также включено параллельно R н, если пренебречь малым сопротивлением r э и 
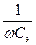между точкой «а» и корпусом C диф э непосредственно шунтирует r э, то есть вход каскада.
Следующий анализ влияния любой из этих ёмкостей можно свести к простой схеме:
.
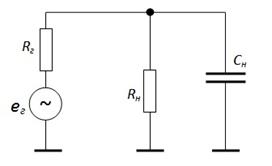
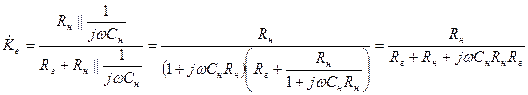Делим числитель и знаменатель на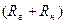 
:
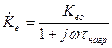, где 
, 
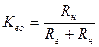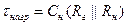- постоянная времени перезаряда ёмкости C н.
Выражение для АЧХ:
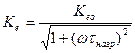
Откуда
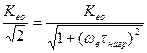или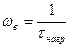 
.
Чтобы ωв увеличить, надо уменьшить постоянную времени перезаряда каждой из ёмкостей C н, C кэ и C диф э.
; 
.
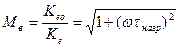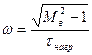Анализ каскада ОЭ на СЧ.
Пренебрегаем реактивностями (считая, что их сопротивления на СЧ равны нулю), получаем более простую эквивалентную схему.
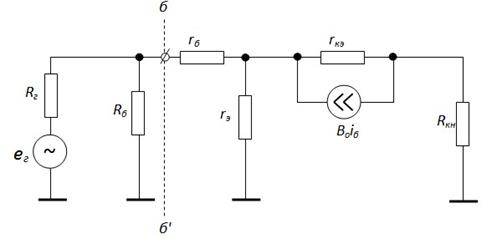Здесь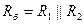 
, 
.
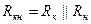Упрощая часть схемы левее бб’, имеем:
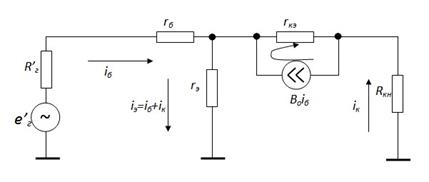Здесь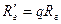 
, 
, 
.
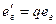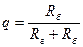Составим уравнения по методу контурных токов:
,
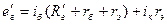
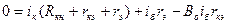так как всегда r э << r кэ, то второе уравнение:
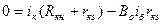, откуда
.
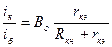Это отношение назовём динамическим коэффициентом усиления транзистора Be:
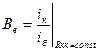, в отличие от 
.
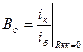Тогда можно нашу эквивалентную схему представить в более удобном виде, состоящей из двух частей: первая часть соответствует первому уравнению, вторая часть – второму уравнению после пренебрежения сопротивлением r э.
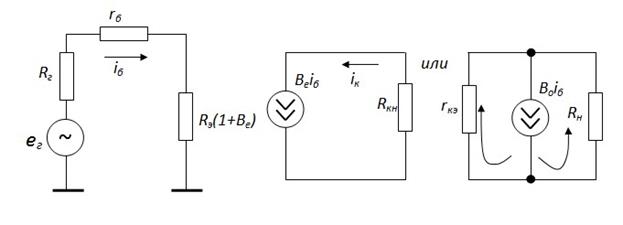Проверьте выполнение уравнений (1) и (2) для этой схемы:
Уравнение (1):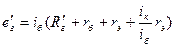 
.
Уравнение (2):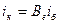 
.
Теперь легко находим все основные параметры каскада (Ku , Ki , Kp , R вх , R вых). Входное сопротивление без учёта R б назовём R вх тр:
.
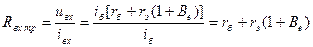С учётом R б:
.
.
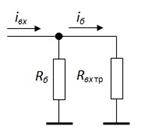
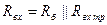
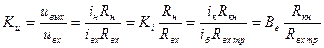
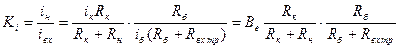
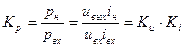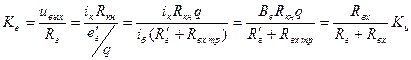
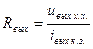Сначала рассмотрим случай, когда R н включено непосредственно в коллекторную цепь (т.е. вместо R к). При этом R вых назовём R вых тр.
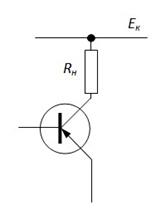
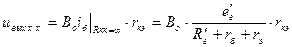, так как Be =0.
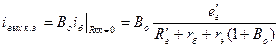, так как Be = Bo.
.
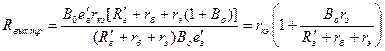В схемах с R к:
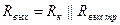и так как обычно 
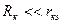, то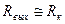 
.
Имеем:
R вх обычно составляет сотни ом-единицы кОм. R вых = R к.
Дата: 2018-12-28, просмотров: 278.
