Терминология: выходные параметры (показатель y_j – это количественная оценка основных свойств схемы). Так для усилителей выходными параметрами являются коэффициенты усиления, входные и выходные сопротивления, граничные частоты и полосы пропускания.

Параметры компонентов схемы – это параметры транзисторов, конденсаторов, катушек индуктивности, трансформаторов, входящих в схему.

Параметры внешних воздействий – параметры входных сигналов, температуры, напряжения источников питания, параметры нагрузки (можно их назвать внешними параметрами).

       Очевидно, что вектор выходных параметров Y есть функция вектора параметров компонентов и внешних воздействий X:

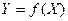 (1)

       В процессе проектирования многократно приходится решать задачу анализа.

       Главная цель анализа электронной схемы – определение Y на основе зависимостей (1). Частными задачами анализа являются:

¾ анализ чувствительности;

¾ анализ устойчивости;

¾ статистический анализ.

Анализ чувствительности – это определение так называемых коэффициентов влияния.

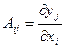 - абсолютный коэффициент влияния (стабилизации).

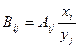- относительный коэффициент влияния.

Лекция 23.

A_ij и B_ij показывают, как x_i влияют на y_j, и следовательно, на какие x_i нужно воздействовать, чтобы получить желаемое изменение y_j.

Анализ устойчивости должен дать ответ на вопрос: является ли схема при данном наборе x_i устойчивой, то есть не возбуждается ли она.

Статистический анализ. Так как параметры компонентов – случайные величины, то и их функции y_j также являются случайными еличинами. Поэтому x_i и характеризуются не только своими математическими ожиданиями, но и дисперсией. Цель статистического анализа – определение законов распределения y_j и числовых характеристик этих законов, в первую очередь M и σ.

Расчёт электронных схем. Задача расчёта в некотором смысле является обратной по отношению к анализу. Цель расчёта – определение x_i, при которых выполняются условия работоспособности

,

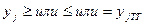где y_{j TT} – значение y_j по технологическим требованиям.

       В случае усилителя условия работоспособности могут быть заданы, например, таким образом:

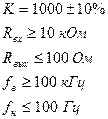
       Очевидно, что условиям работоспособности может удовлетворить не один вектор X (то есть не один набор значений x_i – точка в пространстве параметров x_i), а целая область в пространстве параметров (допустимая область или область устойчивой работы).

Оптимизация электронных схем. Если ставится задача найти не просто какую-либо точку в допустимой области пространства параметров, а оптимальную с точки зрения какого-либо критерия, то это задача оптимизации.

Наконец, разработка вида (структуры) принципиальной схемы вместе с расчётом параметров компонентов есть задача синтеза.

Рассмотрение усилителей в курсе «Общая электроника» - это знакомство с основными схемотехническими решениями – принципиальными схемами, выполнение анализа схем. Полученные при анализе выражения служат основой для формул, используемых при расчётах. Расчёт будем рассматривать только на примерах в частных случаях.

Методы анализа. Прежде всего принципиальная схема заменяется эквивалентной схемой. Математическое описание электрических процессов в эквивалентной схеме представляет собой систему уравнений, получающихся на основе законов Кирхгофа и Ома (математическая модель). В более общем случае математическая модель – это система нелинейных дифференциальных уравнений.

Дифференциальные уравнения получаются из-за наличия реактивностей, для которых

.

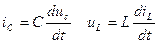Нелинейность уравнений связана с нелинейностью активных компонентов, то есть с непостоянством R , C , L эквивалентных схем активных компонентов.

       Решение системы дифференциальных уравнений даёт зависимости входных и выходных напряжений и токов от времени

       Зная 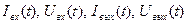, можно определить все основные выходные параметры схемы. Однако решение нелинейных дифференциальных уравнений аналитическими методами возможно в самых простейших случаях. Поэтому в наиболее общей постановке задача анализа должна решаться с помощью ЦВМ (это методы машинного анализа).

       Необходимо упростить задачу анализа. Для малосигнальных схем (а таковыми является большинство усилителей), главный упрощающий приём – раздельный анализ по постоянному току (графо-аналитические методы) и по переменному току. Задача нализа по переменному току становится линейной задачей.

       Для линейных цепей можно перейти от дифференциальных уравнений к алгебраическим, применив способ комплексной частоты. Это удобно, если входные сигналы имеют синусоидальнуб форму или могут быть представлены в виде суммы небольшого числа синусоид (гармоник). Для синусоидальных величин операция дифференцирования может быть заменена умножением на комплексную частоту jω :

.

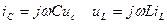       Теперь система дифференциальных уравнений преобразуется в более удобную для решения систему алгебраических уравнений. Результатом решения являются входные и выходные токи и напряжения уже не в виде функции времени, а как функции частоты ω. Основные выходные параметры усилителей также определяются как функции частоты:

.

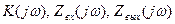       Однако и в этом случае остаются значительные математические трудности, связанные с необходимостью решения алгебраических уравнений с комплексными коэффициентами высокого порядка. Поэтому решение задачи по строго формальному пути приводит обычно к неразрешимым трудностям. Искусство инженера (при использовании нематематических методов) заключается, в частности, в том, чтобы умело упростить задачу, уменьшим число учитываемых реактивностей.

       Так в случае усилителей используется раздельный анализ на высоких, средних и низких частотах. В каждом из этих диапазонов можно учитывать лишь часть реактивностей схемы. Обычно задача становится практически разрешимой, если число учитываемых реактивностей не более двух.

       Таким образом, для выполнения анализа нужно умение составить эквивалентную схему для интересующего диапазона частот и, используя методы анализа линейных электрических цепей, получить формулы для основных выходных параметров.