Глава 1. Общие сведения об электронных усилителях.
Усилители мощности, напряжения и тока.
Усилитель является четырёхполюсником.
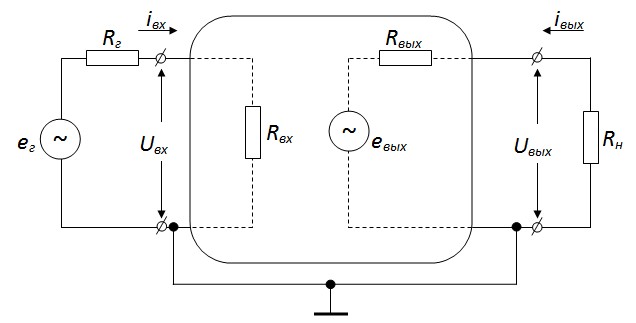
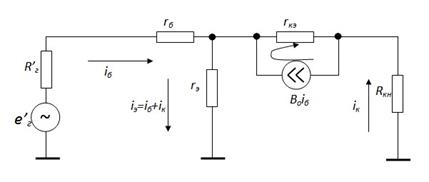
Входное сопротивление: 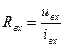 .
.
Выходное сопротивление: 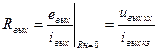 .
.
Коэффициент усиления по мощности:
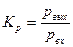 ;
; 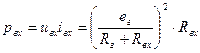 .
.
Если R г задано, но можно выбирать R вх, то максимум p вх будет при согласовании R г = R вх.
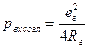 - располагаемая мощность на входе.
- располагаемая мощность на входе.
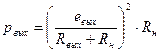 .
.
Для увеличения p вых желательно уменьшать R вых. При заданном R вых максимум p вых будет достигнут при согласовании: R вых = R н.
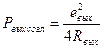 . Тогда
. Тогда 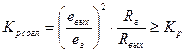 .
.
Kp часто выражают в децибелах:
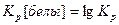 ;
; 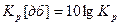 .
.
Если попарно соизмеримы R г и R вх, R вых и R н, то рассматриваемый усилитель – усилитель мощности. Если R н очень велико, то P вых исчезающе мало. Например цепь пластин ЭЛТ. В этом случае нас интересует напряжение в нагрузке, а не мощность. Если велико P вх (например в ламповых усилителях), то также целесообразно говорить о мощности во входной цепи усилителя. Нас тоже интересует напряжение. Итак, при 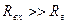 или при
или при 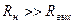 нужно говорить об усилении напряжения:
нужно говорить об усилении напряжения:
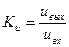 или
или 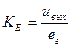 .
.
Если 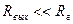 или
или 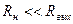 , то лучше усиление характеризовать коэффициентом усиления по току:
, то лучше усиление характеризовать коэффициентом усиления по току:
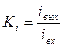
Обычно даже при соизмеримых сопротилениях оценку лучше вести по Ku или Ki, а не по Kp (за исключением выходных каскадов). Это связано с тем, что при расчёте нужно оценивать рабочие участки ВАХ, а они даются в координатах U и I .
Ku и Ki тоже можно выражать в децибелах. При этом:
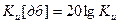 и
и 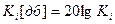 .
.
| Ku | 1 | 1,41 | 10 | 100 | 1000 |
| Ku[ дб ] | 0 | 3 | 20 | 40 | 60 |
Нетрудно заметить, что 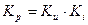 .
.
Многокаскадные усилители.
Понятие каскада можно проиллюстрировать следующим рисунком.
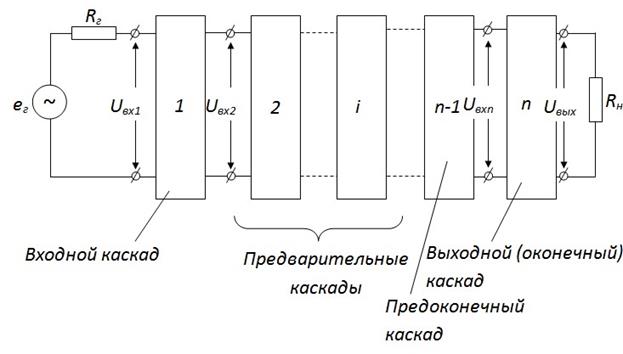
Коэффициент усиления усилительного каскада из n ступеней определяется следующим образом:
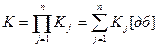 .
.
Способы связи каскадов между собой, а также способ включения нагрузки к выходу усилителя определяют многие важные свойства усилителя.
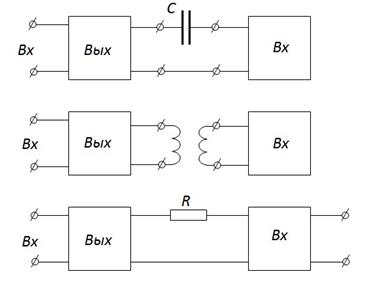 Типы межкаскадных связей:
Типы межкаскадных связей:
RC-усилители. Ёмкость даёт возможность разделить каскады по постоянному току, что удобно.
Трансформаторные сязи обладают как преимуществами, так и недостатками.
Гальванические (непосредственные) связи. Используются на инфранизких чатсотах и в УПТ.
Классы усиления.
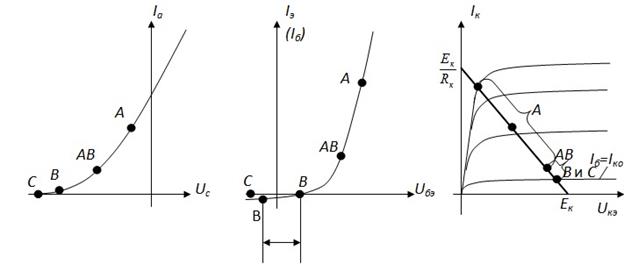
В зависимости от положения рабочей точки различают четыре класса усиления: А – рабочая точка находится на линейном участке (часто в его середине), AB – рабочая точка находится на границе линейного участка, ближе к области малых токов, B – рабочая точка находится запирания, то есть в точке, где Ia =0 или 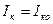 , C – смещение рабочей точки таково, что её положение оказывается левее (на входных характеристиках) точки запирания электронного прибора.
, C – смещение рабочей точки таково, что её положение оказывается левее (на входных характеристиках) точки запирания электронного прибора.
От выбора положения рабочей точки усилителя зависит:
· величина нелинейных искажений;
· КПД;
· коэффициент усиления;
· уровень шумов;
· динамический диапазон.
Например, в классе B угол отсечки составляет примерно 90°, что влечёт нелинейные искажения, поэтому применяются только в двухтактных каскадах.
Класс AB является промежуточным, угол отсечки ≈120-130°. Возможно применение только в двухтактных каскадах, даёт меньшие нелинейные искажения, чем класс B.
Применение класса C возможно только в импульсных схемах.
Лекция 20.
Лекция 21.
Перейдём к количественному рассмотрению стабилизации.
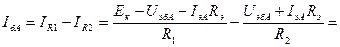
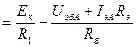 , где
, где 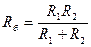 .
.
Так как 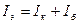 , получаем
, получаем
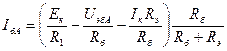
Найдём отсюда 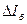 и подставим его в (2):
и подставим его в (2):
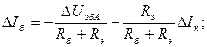
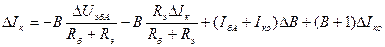 .
.
Выразим 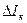 в явном виде:
в явном виде:
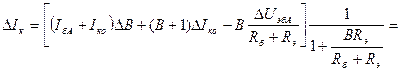
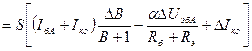 (3),
(3),
где 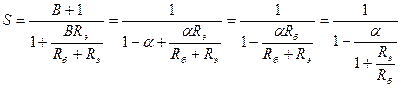 (4)
(4)
Таким образом, 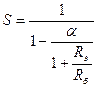 .
.
S – коэффициент нестабильности, по-прежнему имеющий смысл производной 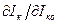 . Варажения (3) и (4) оказываются достаточно общими и справедливыми для различных схем смещения.
. Варажения (3) и (4) оказываются достаточно общими и справедливыми для различных схем смещения.
Так для схемы на германиевых транзисторах с фиксированным током базы R э =0, R б достаточно велико, членом с 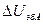 можно пренебречь,
можно пренебречь, 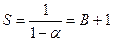 . Из (4) видно, что увеличение R э и уменьшение R б приближают S к 1. В пределе S =1 при
. Из (4) видно, что увеличение R э и уменьшение R б приближают S к 1. В пределе S =1 при 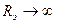 и
и 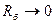 . В этом идеальном случае:
. В этом идеальном случае:
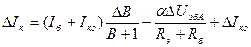 .
.
Поэтому S можно ещё определить как отношение 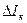 в реальной схеме к
в реальной схеме к 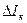 в схеме с идеальной термостабилизацией.
в схеме с идеальной термостабилизацией.
Практически получить 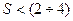 в схемах с одним источником питания
в схемах с одним источником питания 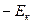 не удастся. Действительно, увеличение R э приводит к неразумному использованию E к: большая его часть падает на R э и снижает динамический диапазон выходного напряжения. Уменьшение R б снижает входное сопротивление каскада, так как:
не удастся. Действительно, увеличение R э приводит к неразумному использованию E к: большая его часть падает на R э и снижает динамический диапазон выходного напряжения. Уменьшение R б снижает входное сопротивление каскада, так как:
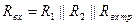 .
.
Кроме того, чтобы при 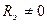 не снижалось усиление каскада, R э шунтируют конденсатором C э, при этом бесполезного падения напряжения сигнала на R э не будет. C э должно быть достаточно большим, чтобы постоянная времени перезаряда этого конденсатора превышала бы в несколько раз период самых низкочастотных составляющих сигнала.
не снижалось усиление каскада, R э шунтируют конденсатором C э, при этом бесполезного падения напряжения сигнала на R э не будет. C э должно быть достаточно большим, чтобы постоянная времени перезаряда этого конденсатора превышала бы в несколько раз период самых низкочастотных составляющих сигнала.
Подобная же схема смещения используется и при включении транзистора по схеме ОБ и ОК.
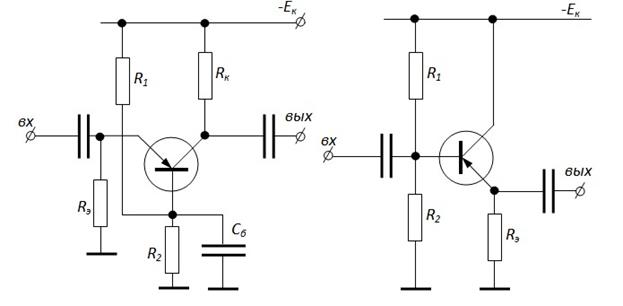 ОБ: отличие от ОЭ только в том, что C б заземляет по переменному току базу, а не эмиттер.
ОБ: отличие от ОЭ только в том, что C б заземляет по переменному току базу, а не эмиттер.
ОК: если R э больше либо равно требуемому сопротивлению, то цепь 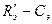 отсутствует и блокировочного конденсатора не нужно; если R э мало, то для повышения стабильности включают
отсутствует и блокировочного конденсатора не нужно; если R э мало, то для повышения стабильности включают 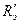 и шунтируют его C э. Расчёт цепей смещения при наличии термостабилизации производят следующим образом:
и шунтируют его C э. Расчёт цепей смещения при наличии термостабилизации производят следующим образом:
Исходные данные: определено положение рабочей точки, т.е. I бА, I кА, U кА, U эбА.
а) Выбирается R э так, чтобы падение напряжения на нём не превышало 10-25% от E к, то есть:
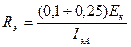 .
.
б) Задаются коэффициентом нестабильности S (рекомендуется около 4). Тогда емеем два уравнения с двумя неизвестными R 1 и R 2:
1. 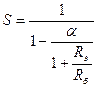 , где
, где 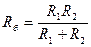 .
.
2. 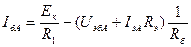 .
.
Из 1) находим R б:
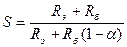 ;
; 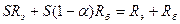 ;
; 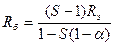 .
.
Из 2) находим R 1:
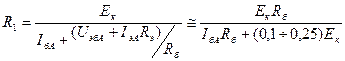
(пренебрегаем U эбА).
в) Определяем R 2 из выражения для R б:
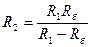 .
.
Пример. Задано E к =15 В, I бА =20 мкА, α=0,98.
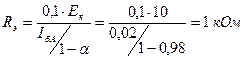 .
.
Задаёмся S = 4.
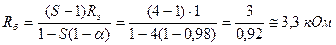 .
.
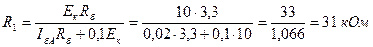 .
.
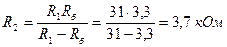 .
.
Из этого примера видно, что R вх каскада будет меньше 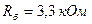 . В тех случаях, когда к R вых предъявляются жёсткие требования, то задают не S, а R б, находят R 1 и R 2 и проверяют получившееся S. Пусть
. В тех случаях, когда к R вых предъявляются жёсткие требования, то задают не S, а R б, находят R 1 и R 2 и проверяют получившееся S. Пусть 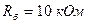 . Тогда:
. Тогда:
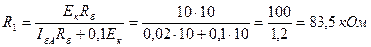 .
.
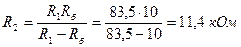 .
.
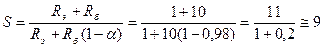 .
.
Другой используемой на практике схемой термостабилизации является изображённая на рисунке ниже.
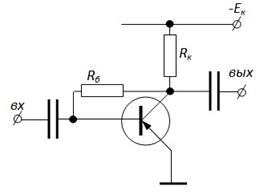 По заданной рабочей точке (U кА, I бА) определяется R б:
По заданной рабочей точке (U кА, I бА) определяется R б:
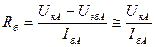 .
.
В этой схеме по R к протекает ток 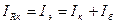 . При увеличении температуры
. При увеличении температуры 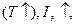 а
а 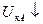 , и как следствие
, и как следствие 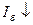 . То есть рост I к здесь тоже замедлен из-за уменьшения I б. К этой схеме применяются полученные для
. То есть рост I к здесь тоже замедлен из-за уменьшения I б. К этой схеме применяются полученные для 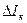 и S формулы (3) и (4), только вместо R э в эти формулы подставляется сопротивление R к.
и S формулы (3) и (4), только вместо R э в эти формулы подставляется сопротивление R к.
Следует отметить, что повышение стабильности положения рабочей точки является следствием применения в рассматриваемых схемах отрицательной обратной связи. В предыдущей схеме:
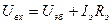 , то есть на входе схемы присутствовало напряжение
, то есть на входе схемы присутствовало напряжение 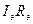 , зависящее от выходного тока. С помощью C э обратная связь на переменном токе устарнялась и снижения усиления не было. В последней схеме выход связан со входом непосредственно через R б. Наличие обратной связи снижает усиление. Чтобы этого не происходило, можно применить следующую схему (см. рисунок).
, зависящее от выходного тока. С помощью C э обратная связь на переменном токе устарнялась и снижения усиления не было. В последней схеме выход связан со входом непосредственно через R б. Наличие обратной связи снижает усиление. Чтобы этого не происходило, можно применить следующую схему (см. рисунок).
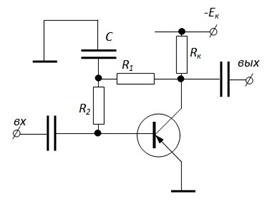 По постоянному току здесь нет отличия от предыдущей схемы, если
По постоянному току здесь нет отличия от предыдущей схемы, если 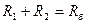 . По переменному току обратная связь устраняется с помощью конденсатора C, заземляющего среднюю точку делителя R 1 – R 2.
. По переменному току обратная связь устраняется с помощью конденсатора C, заземляющего среднюю точку делителя R 1 – R 2.
Схема со связью базы и коллектора через R б применяется реже, так как здесь трудно добиться желательного S, ибо R к и R б выбираются из других соображений, а не исходя из требуемой стабильности.
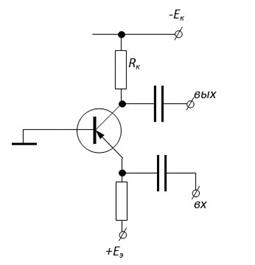
В случае схемы ОБ и при двух источниках питания достикается S =1.
 Лекция 22.
Лекция 22.
Действительно, здесь 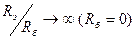 и S =1.
и S =1.
То есть именно эту схему можно считать идеальной с точки зрения стабильности положения рабочей точки. Добиться S <1 можно только используя цепи термокомпнсации.
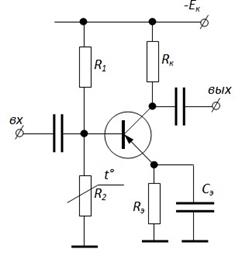
В качестве R 2 используется термочувствительный элемент (терморезистор или полупроводниковый диод) с отрицательным ТК.
Термокомпенсация используется реже, так как трудно подбирать термочувствительные жлементы с нужным ТК.
В заключение несколько разновидностей рассматриваемых схем.
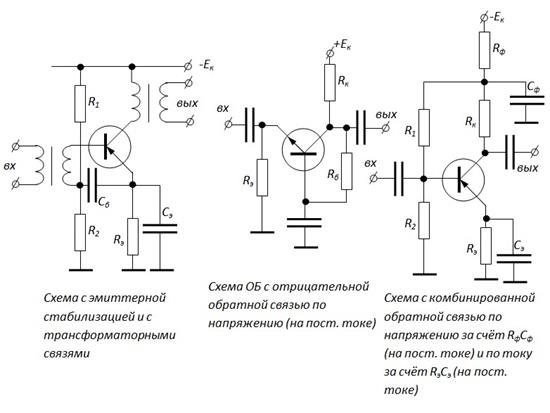
Следует отметить, что вывод о желательности уменьшения R б в полной мере относится к схемам на германиевых транзисторах. В схемах с кремниевыми транзисторами I ко настолько мал, что членом с 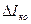 в выражении (3) можно пренебречь. Тогда большую роль в нестабильности положения рабочей точки начинает играть член с
в выражении (3) можно пренебречь. Тогда большую роль в нестабильности положения рабочей точки начинает играть член с 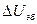 . Если пренебречь
. Если пренебречь 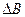 , то
, то
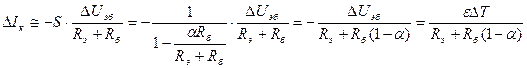 (знак «+», так как ε отрицательно).
(знак «+», так как ε отрицательно).
Тогда для уменьшения 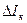 нужно увеличивать как R э, так и R б. Для принятия окончательного решения о R б нужно при кремниевых транзисторах оценить относительный вклад в
нужно увеличивать как R э, так и R б. Для принятия окончательного решения о R б нужно при кремниевых транзисторах оценить относительный вклад в 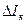 членов с
членов с 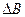 и с
и с 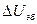 , то есть знать величину ε и температурную зависимость коэффициента B.
, то есть знать величину ε и температурную зависимость коэффициента B.
Лекция 23.
Aij и Bij показывают, как xi влияют на yj, и следовательно, на какие xi нужно воздействовать, чтобы получить желаемое изменение yj.
Анализ устойчивости должен дать ответ на вопрос: является ли схема при данном наборе xi устойчивой, то есть не возбуждается ли она.
Статистический анализ. Так как параметры компонентов – случайные величины, то и их функции yj также являются случайными еличинами. Поэтому xi и характеризуются не только своими математическими ожиданиями, но и дисперсией. Цель статистического анализа – определение законов распределения yj и числовых характеристик этих законов, в первую очередь M и σ.
Расчёт электронных схем. Задача расчёта в некотором смысле является обратной по отношению к анализу. Цель расчёта – определение xi, при которых выполняются условия работоспособности
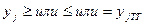 ,
,
где yj TT – значение yj по технологическим требованиям.
В случае усилителя условия работоспособности могут быть заданы, например, таким образом:
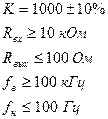
Очевидно, что условиям работоспособности может удовлетворить не один вектор X (то есть не один набор значений xi – точка в пространстве параметров xi), а целая область в пространстве параметров (допустимая область или область устойчивой работы).
Оптимизация электронных схем. Если ставится задача найти не просто какую-либо точку в допустимой области пространства параметров, а оптимальную с точки зрения какого-либо критерия, то это задача оптимизации.
Наконец, разработка вида (структуры) принципиальной схемы вместе с расчётом параметров компонентов есть задача синтеза.
Рассмотрение усилителей в курсе «Общая электроника» - это знакомство с основными схемотехническими решениями – принципиальными схемами, выполнение анализа схем. Полученные при анализе выражения служат основой для формул, используемых при расчётах. Расчёт будем рассматривать только на примерах в частных случаях.
Методы анализа. Прежде всего принципиальная схема заменяется эквивалентной схемой. Математическое описание электрических процессов в эквивалентной схеме представляет собой систему уравнений, получающихся на основе законов Кирхгофа и Ома (математическая модель). В более общем случае математическая модель – это система нелинейных дифференциальных уравнений.
Дифференциальные уравнения получаются из-за наличия реактивностей, для которых
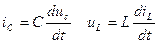 .
.
Нелинейность уравнений связана с нелинейностью активных компонентов, то есть с непостоянством R , C , L эквивалентных схем активных компонентов.
Решение системы дифференциальных уравнений даёт зависимости входных и выходных напряжений и токов от времени
Зная 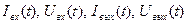 , можно определить все основные выходные параметры схемы. Однако решение нелинейных дифференциальных уравнений аналитическими методами возможно в самых простейших случаях. Поэтому в наиболее общей постановке задача анализа должна решаться с помощью ЦВМ (это методы машинного анализа).
, можно определить все основные выходные параметры схемы. Однако решение нелинейных дифференциальных уравнений аналитическими методами возможно в самых простейших случаях. Поэтому в наиболее общей постановке задача анализа должна решаться с помощью ЦВМ (это методы машинного анализа).
Необходимо упростить задачу анализа. Для малосигнальных схем (а таковыми является большинство усилителей), главный упрощающий приём – раздельный анализ по постоянному току (графо-аналитические методы) и по переменному току. Задача нализа по переменному току становится линейной задачей.
Для линейных цепей можно перейти от дифференциальных уравнений к алгебраическим, применив способ комплексной частоты. Это удобно, если входные сигналы имеют синусоидальнуб форму или могут быть представлены в виде суммы небольшого числа синусоид (гармоник). Для синусоидальных величин операция дифференцирования может быть заменена умножением на комплексную частоту jω :
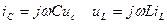 .
.
Теперь система дифференциальных уравнений преобразуется в более удобную для решения систему алгебраических уравнений. Результатом решения являются входные и выходные токи и напряжения уже не в виде функции времени, а как функции частоты ω. Основные выходные параметры усилителей также определяются как функции частоты:
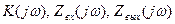 .
.
Однако и в этом случае остаются значительные математические трудности, связанные с необходимостью решения алгебраических уравнений с комплексными коэффициентами высокого порядка. Поэтому решение задачи по строго формальному пути приводит обычно к неразрешимым трудностям. Искусство инженера (при использовании нематематических методов) заключается, в частности, в том, чтобы умело упростить задачу, уменьшим число учитываемых реактивностей.
Так в случае усилителей используется раздельный анализ на высоких, средних и низких частотах. В каждом из этих диапазонов можно учитывать лишь часть реактивностей схемы. Обычно задача становится практически разрешимой, если число учитываемых реактивностей не более двух.
Таким образом, для выполнения анализа нужно умение составить эквивалентную схему для интересующего диапазона частот и, используя методы анализа линейных электрических цепей, получить формулы для основных выходных параметров.
Анализ каскада ОЭ на СЧ.
Пренебрегаем реактивностями (считая, что их сопротивления на СЧ равны нулю), получаем более простую эквивалентную схему.
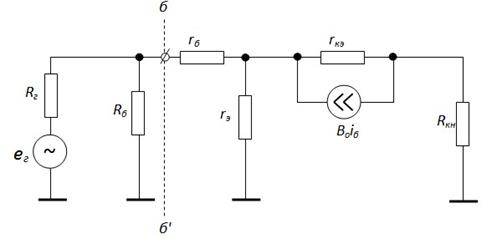 Здесь
Здесь 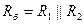 ,
, 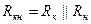 .
.
Упрощая часть схемы левее бб’, имеем:
 Здесь
Здесь 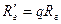 ,
, 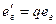 ,
, 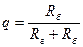 .
.
Составим уравнения по методу контурных токов:
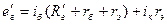
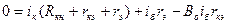 ,
,
так как всегда r э << r кэ, то второе уравнение:
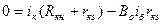 , откуда
, откуда
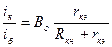 .
.
Это отношение назовём динамическим коэффициентом усиления транзистора Be:
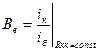 , в отличие от
, в отличие от 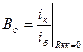 .
.
Тогда можно нашу эквивалентную схему представить в более удобном виде, состоящей из двух частей: первая часть соответствует первому уравнению, вторая часть – второму уравнению после пренебрежения сопротивлением r э.
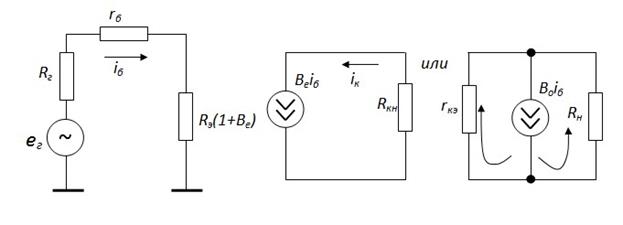 Проверьте выполнение уравнений (1) и (2) для этой схемы:
Проверьте выполнение уравнений (1) и (2) для этой схемы:
Уравнение (1): 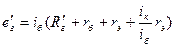 .
.
Уравнение (2): 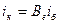 .
.
Теперь легко находим все основные параметры каскада (Ku , Ki , Kp , R вх , R вых). Входное сопротивление без учёта R б назовём R вх тр:
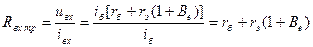 .
.
С учётом R б:
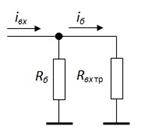
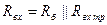
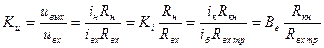
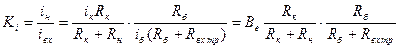
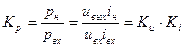 .
.
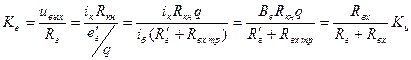
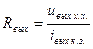 .
.
Сначала рассмотрим случай, когда R н включено непосредственно в коллекторную цепь (т.е. вместо R к). При этом R вых назовём R вых тр.
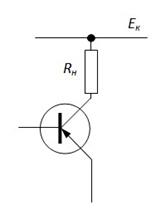
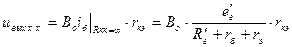 , так как Be =0.
, так как Be =0.
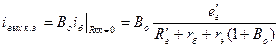 , так как Be = Bo.
, так как Be = Bo.
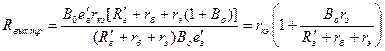 .
.
В схемах с R к:
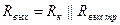 и так как обычно
и так как обычно 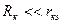 , то
, то 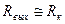 .
.
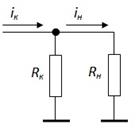
Имеем:
R вх обычно составляет сотни ом-единицы кОм. R вых = R к.
Лекция 25.
Глава 1. Общие сведения об электронных усилителях.
Дата: 2018-12-28, просмотров: 471.