При сжатии бетонной призмы в режиме пропорциональ­ного развития во времени продольных деформаций об­наруживается постепенное снижение сопротивления бето­на, так называемая ниспадающая ветвь диаграммы на­пряжения — деформации. Такой участок повышенного деформирования бетона реально наблюда­ется в конструкциях при определенных условиях нагружения, например, при сжатии бетона у внешней грани сжатой зоны изгибаемых элементов. При длительном действии нагрузки неупругие деформации бетона с течением времени увеличиваются. Наибольшая интенсивность нарастания неупругих деформаций наблю­дается первые 3…4 мес. и может продолжаться несколь­ко лет. На диаграмме(рис.17) участок 0—1 харак­теризует деформации, возникающие при загружении (его кривизна зависит от скорости загружения); участок 1—2 характеризует нарастание неупругих деформаций при постоянном значении напряжении.

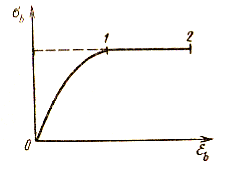Рис.17. Диаграмма σ_b - Ɛ_bпри длительномзагружении бетона.

Свойства бетона, характеризующиеся нарастанием не­упругих деформаций с течением времени при постоянных напряжениях, называют ползучестью бетона. Деформа­ции ползучести могут в 3…4 раза превышать упругие деформации. При длительном действии постоянной на­грузки, если деформации ползучести нарастают свободно, напряжения в бетоне остаются постоянными. Когда же связи в бетоне (например, стальная арматура) ограни­чивают свободное развитие ползучести (стесненная пол­зучесть), то напряжения в бетоне уменьшаются. Свой­ство бетона, характеризующееся уменьшением с течени­ем времени напряжений при постоянной начальной деформации 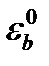, называют релаксацией напряжений. Ползучесть и релаксация имеют общую природу и ока­зывают существенное влияние на работу железобетонных конструкций под нагрузкой.

Природа ползучести бетона объясняется его структу­рой, длительным процессом кристаллизации и уменьше­нием количества геля при твердении цементного камня. Под нагрузкой происходит перераспределение напряже­ний с испытывающей вязкое течение гелевой структурной составляющей на кристаллический сросток и зерна за­полнителей. Одновременно развитию деформаций ползу­чести способствуют капиллярные явления, связанные с перемещением в микропорах и капиллярах избыточной воды под нагрузкой. С течением времени процесс пере­распределения напряжений затухает и деформирование прекращается.

Под мерой ползучести C_bпонимают относительную деформацию ползучести бетона при σ_b 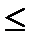0,3 R_bn, накопившуюся к моменту времени t при загружении образцов в t ₀< 1 и приходящуюся на 1 МПа действующего постояного напряжения:

C_b ( t , t ₀ )= Ɛ _cr ( t , t ₀ )/σ _b

Заменив Ɛ _cr =λƐ _bиσ _b = Е’ _b Ɛ _b =ν Е _b Ɛ _bнаходят:

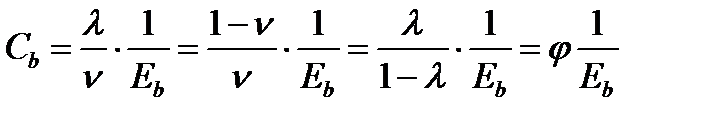
где φ = λ/ν = (1- λ)/ ν = λ/(1- λ) – так называемая характеристика нелинейности деформирования бетона; φ может меняться от 0 до ∞, поэтому удобнее пользоваться коэффициентами λ и ν.

Система определений, гипотез и уравнений между характеристиками ползучести и простой ползучести составляет содержание теорий ползучести. Для бетонов были разработаны две теории ползучести, исходя из основных свойств деформирования бетонов: теория старения и теория наследственности. Общими для всех современных теорий ползучести бетонов является гипотеза о синхронности развития во времени продольных и поперечных деформаций (еще достаточно не исследованная), допущения о взаимнонезависимости и малости частных деформаций и гипотеза о суперпозиции деформации ползучести (две последние экспериментально подтверждаются приближенно).

В качестве основной гипотезы теории старения, а так же ее вариантов положена предпосылка, что меры деформаций ползучести при любом монотонном режиме загруженияравны приращениям меры деформаций простой ползучести или, что то же самое, допущение о параллельности кривых ползучести и кривых постой ползучести:

C_b ( t , τ )= С₀( t , t ₀ ) - С₀( τ , t ₀ )

где τ – текущая координата времени; t – момент конечного наблюдения деформаций; t ₀– момент начала нагружения.

Как показывают эксперименты, теория старения преувеличивает влияние старения материала и преуменьшает расчетные значения деформаций ползучести.

В качестве основной гипотезы теории наследственности положена предпосылка, что меры деформации ползучести при любом монотонном режиме загружения равны мере деформации простой ползучести

C ( τ , t )= C ₀ ( τ , t )

Обе указанные теории дают некоторые предельные значения деформации ползучести: наименьшие и наибольшие. Кроме того, как показал анализ, в ряде случаев использование теории старения может привести к качественным несоответствиям. Основной причиной ее существования и дальнейшего применения является относительная математическая простота, состоящая в элементарном переходе от интегральных к дифференциальным уравнениям состояния.