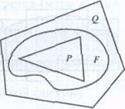
Пусть F - произвольная плоская фигура. В геометрии считают, что она имеет площадь S(F), если выполняются следующие условия: сущест­вуют многоугольные фигуры, которые содер­жат F (назовем их объемлющими); существуют многоугольные фигуры, которые содержатся в F (назовем их входящими); площади этих мно­гоугольных фигур как угодно мало отличаются от S(F). Поясним эти положения. На рисунке показано, что фигу­ра Q содержит фигуру F , т.е. Q - объемлющая фигура, а фигура Р содержится в F, т.е. Р - входящая фигура. На теоретико-множествен­ном языке это означает, что

 Р ⊂ F ⊂Q следовательно, можно записать, что S(Р)≦ S(F) ≦ S(Q).

Если разность площадей объемлющей и входящей фигур может стать как угодно малой, то, как установлено в математике, существует един­ственное число S(F), удовлетворяющее неравенству S(Р)≦ S(F) ≦ S(Q) для любых многоугольных фигур Р и Q. Данное число и считают площадью фигуры F.

Этими теоретическими положениями пользуются, например, когда выводят формулу площади круга. Для этого в круг радиуса r вписы­вают правильный n-угольник Р, а около окружности описывают пра­вильный n- угольник Q. Если обозначить символами S(Q)  и S(Р)пло­щади этих многоугольников, то будем иметь, что S(Р)≦ S(F) ≦ S(Q), причем при возрастании числа сторон вписанных и описанных много­угольников площади S(Р) будут увеличиваться, оставаясь при этом меньше площади круга, а площади S(Q) будут уменьшаться, но оста­ваться больше площади круга.

Площадь правильного n-угольника равна половине произведения его периметра на радиус вписанной в него окружности. При возрас­тании числа его сторон периметр стремится к длине окружности 2πr, а площадь - к площади круга. Поэтому S = 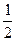 • 2πr • r = πr².

Для приближенного измерения площадей плоских фигур можно использовать различные приборы, в частности, палетку.

Палетка - это прозрачная пластина, на которой нанесена сеть квадратов. Сторона квадрата принимается за 1, и чем меньше эта сторона, тем точнее можно измерить площадь фигуры.

Накладываем палетку на данную фигуру F. Квадраты, которые цели­ком лежат внутри фигуры F, образуют многоугольную фигуру F; квадра­ты, имеющие с фигурой F общие точки и целиком лежащие внутри фигуры F

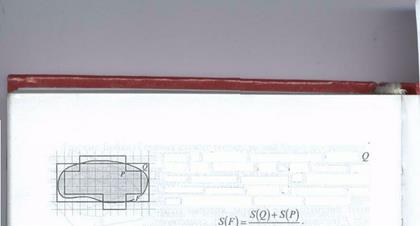
образуют многоугольную фигуру Q. Площади S(Р) и  S(Q) находят про­стым подсчетом квадратов. За приближенное значение площади фигуры F  принимается сред­нее арифметическое найденных площадей: S(F) = (S(Р) + S(Q))/2.

В начальном курсе математики учащиеся измеряют площади фигур с помощью палет­ки таким образом: подсчитывают число квадратов, которые лежат внутри фигуры F, и число квадратов, через которые проходит контур фигуры; затем второе число делят пополам и прибавляют к первому. Полученную сумму считают площадью фигуры F.

Палетка позволяет измерить площадь фигуры F с определенной точностью. Чтобы получить более точный результат, нужно взять па­летку с более мелкими квадратами. Но можно поступить иначе: нало­жить одну и ту же палетку на фигуру по-разному и найти несколько приближенных значений площади фигуры F. Их среднее арифметиче­ское может быть лучшим приближением к численному значению пло­щади фигуры F.

Упражнения

1. На фигуру F наложили палетку и подсчитали, что внутри фигу­ры F  содержится фигура, составленная из 28 единичных квадратов, а фигура F  содержится внутри фигуры, состоящей из 35 единичных квад­ратов. Каково приближенное значение площади фигуры F.

2. Начертите круг радиуса 2 см на клетчатой бумаге и найдите его площадь, используя клетчатую бумагу как палетку, состоящую из квадратов со стороной, равной: а) 1 см; б) 0,5 см. Вычислите площадь этого круга по формуле, приняв π = 3,14. Сравните полученные результаты.

Основные выводы

В данном параграфе мы уточнили ряд понятий, известных из школьного курса математики:

- длина отрезка, численной значение длины отрезка (мера длины отрезка);

величина угла; численное значение величины угла (мера величины угла);

площадь фигуры; численное значение площади фигуры (мера площади фигуры);

площадь многоугольника и произвольной плоской фигуры;

равновеликие и равносоставленные фигуры.

Вспомнили косвенные способы вычисления площадей прямоугольника, треугольника, параллелограмма, произвольного многоугольника, рассмотрели теоремы о взаимосвязи равновеликости и равносоставленности многоугольных фигур; обосновали способ измерения площади фигуры при помощи палетки.

Отметили, что длина, площадь, величина угла характеризуются одинаковыми свойствами, но заданы на разных классах фигур: длина – на множестве отрезков, площадь – на множестве многоугольных и криволинейных фигур; величина угла – на множестве углов.