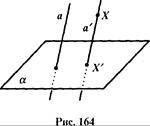
Пусть даны плоскость α и пересекаю­щая ее прямая а. Возьмем в пространстве произвольную точку X, не принадлежа­щую прямой а и проведем через Х пря­мую а', параллельную прямой а (рис.). Прямая а' пересекает плоскость в неко­торой точке X'', которая называется па­раллельной проекцией точки Х на плос­кость а.

Если точка Х лежит на прямой а, то ее параллельной проекцией X' является точка, в которой прямая а пересекает плоскость α.

Если точка Х принадлежит плоскости а, то точка X' совпадает с точкой X.

Таким образом, если заданы плоскость α  и пересекающая ее пря­мая а, то каждой точке Х пространства можно поставить в соответст­вие единственную точку X' - параллельную проекцию точки Х на плоскость α  (при проектировании параллельно прямой а). Плоскость α  называется плоскостью проекций. О прямой а говорят, что она зада­ет направление проектирования - при замене прямой а любой другой параллельной ей прямой результат проектирования не изменится. Все прямые, параллельные прямой а, задают одно и то же направление проектирования и называются вместе с прямой а проектирующими прямыми.

Проекцией фигуры F называется множество F проекцией всех ее то­чек. Отображение, сопоставляющее каждой точке Х фигуры F ее па­раллельную проекцию - точку X' фигуры F, называется параллельным проектиро­ванием фигуры F (рис.).

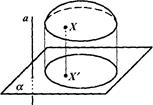
Параллельной проекцией реального предмета является его тень, падающая на плоскую поверхность, при солнечном ос­вещении, поскольку солнечные лучи мож­но считать параллельными.

Параллельное проектирование облада­ет рядом свойств, знание которых необхо­димо при изображении геометрических тел на плоскости. Сформулируем основные, опустив их доказательство.

Теорема. При параллельном проектировании для прямых, не параллельных направлению проектирования, и для лежащих на них отрезков выполняются следующие свойства:

1. Проекция прямой есть прямая, а проекция отрезка - отрезок.

2. Проекции параллельных прямых параллельны или совпадают.

3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

Из этой теоремы вытекает следствие: при параллельном проекти­ровании середина отрезка проектируется в середину его проекции.

При изображении геометрических тел на плоскости необходимо следить за тем, чтобы указанные свойства выполнялись. В остальном оно может быть произвольным. Так, углы и отношения длин непарал­лельных отрезков могут изменяться произвольно, т.е., например, тре­угольник при параллельном проектировании изображается произ­вольным треугольником. Но если треугольник равносторонний, то на проекции его медиана должна соединять вершину треугольника с серединой противоположной стороны.

И еще одно требование необходимо соблюдать при изображении пространственных тел на плоскости - это способствовать созданию верного представления о них.

Упражнения

1. Верно ли, что при параллельном проектировании проекцией па­раллелограмма будет произвольный параллелограмм?

2. Каким будет при параллельном проектировании изображение прямоугольника? ромба? квадрата?

3. Как найти при параллельном проектировании проекцию точки пересечения высот равностороннего треугольника?