Пусть функция 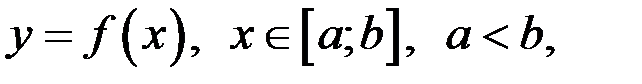 определена и непрерывная на отрезке
определена и непрерывная на отрезке 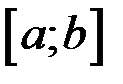 и пусть, для определенности,
и пусть, для определенности, 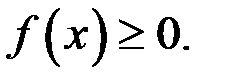
Разобьем отрезок 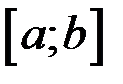 на n частей произвольным образом точками деления:
на n частей произвольным образом точками деления: 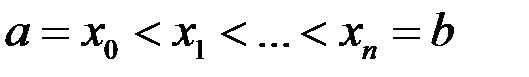 . Выберем на каждом частичном промежутке
. Выберем на каждом частичном промежутке 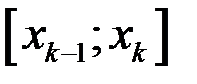 произвольным образом точки
произвольным образом точки 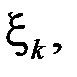
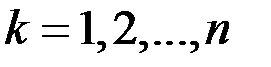 .
.
Обозначим 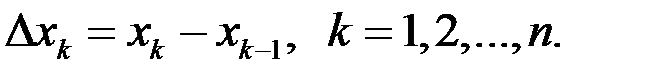 Составим сумму
Составим сумму 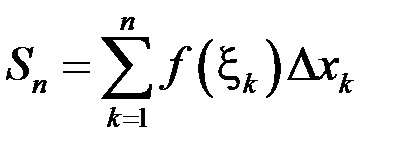 , которая называется интегральной суммой для функции
, которая называется интегральной суммой для функции 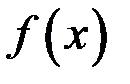 на отрезке
на отрезке 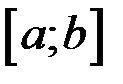 .
.
Обозначим длину наибольшего частичного промежутка через 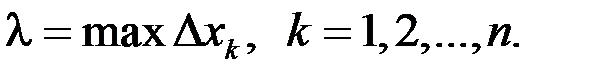 Перейдем к пределу при
Перейдем к пределу при 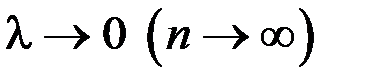 .
.
Если существует конечный предел 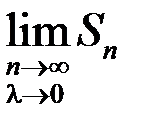 , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка 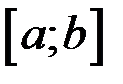 на частичные и выбора на них точек
на частичные и выбора на них точек 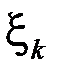 , то он и называется определенным интегралом от функции
, то он и называется определенным интегралом от функции 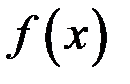 на отрезке
на отрезке 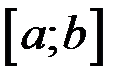 и обозначается
и обозначается
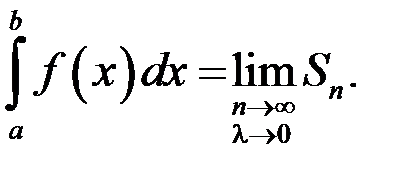
Если 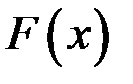 – любая первообразная для функции
– любая первообразная для функции 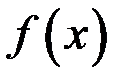 , то справедлива формула Ньютона – Лейбница:
, то справедлива формула Ньютона – Лейбница:
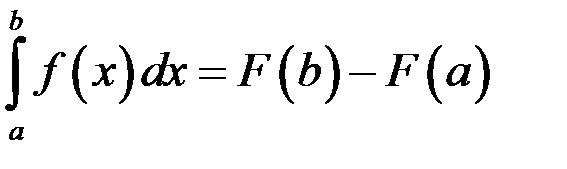 ,
,
т.е. для вычисления определенного интеграла от непрерывной функции 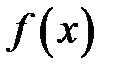 нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
нужно составить разность значений произвольной ее первообразной для верхнего и нижнего пределов интегрирования.
Пример 1
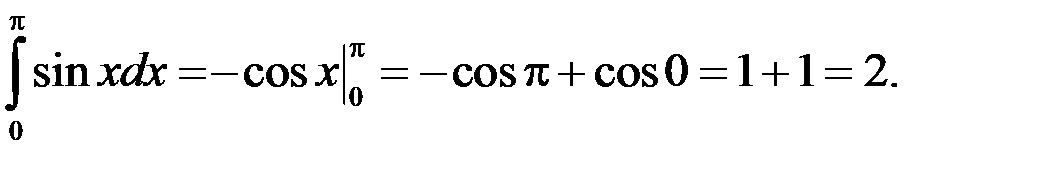
Если 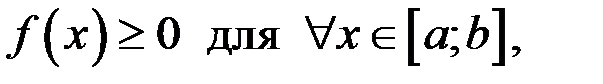 то
то 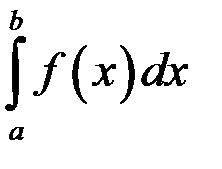 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 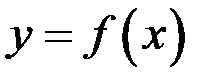 ,
,
прямыми 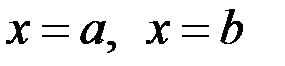 и осью ох:
и осью ох:
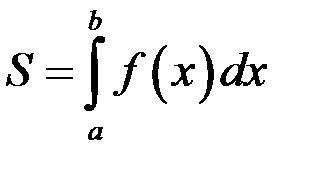
Если 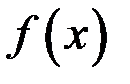 меняет знак конечное число раз на отрезке
меняет знак конечное число раз на отрезке 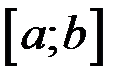 , то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где
, то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где 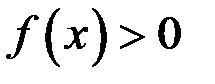 и отрицателен, где
и отрицателен, где 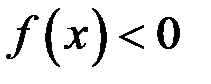 :
:
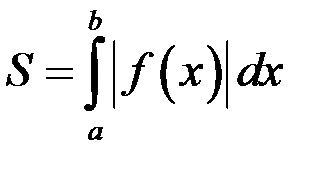 .
.
Пусть нужно вычислить площадь фигуры, ограниченной кривыми 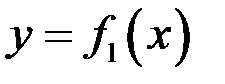 и
и 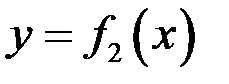 и прямыми
и прямыми 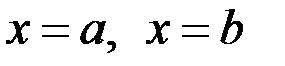 , тогда при условии
, тогда при условии 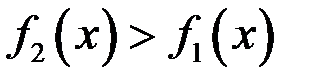 имеем
имеем
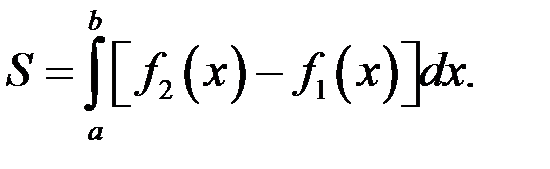
Пример 2
Вычислить площадь фигуры, ограниченной линиями 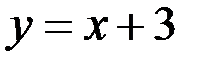 и
и 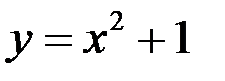 .
.
Решение
| у у=х+3 у=х2+1 3 –3 –1 0 2 х | Найдем точки пересечения: 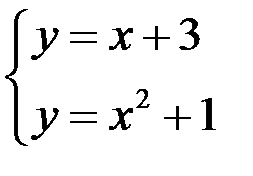 , , 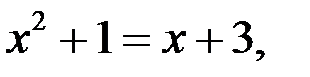
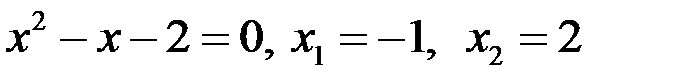 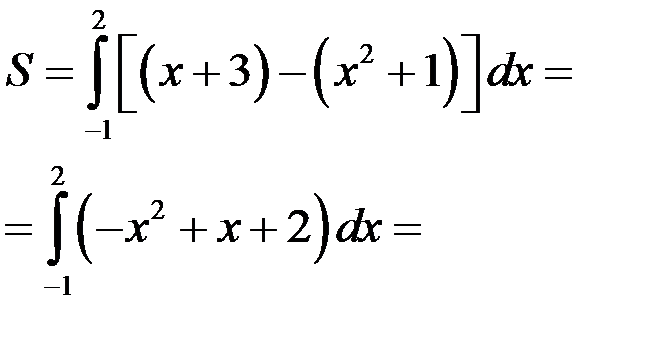
|
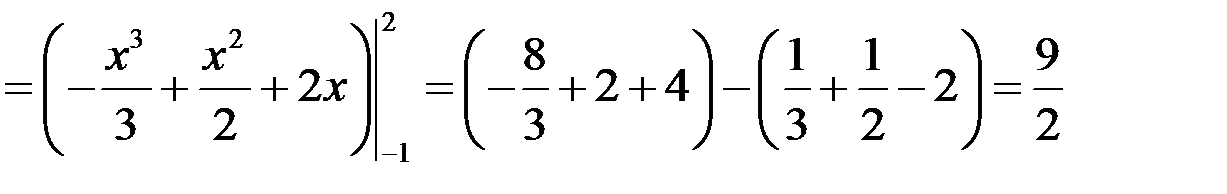 .
.
Контрольная работа № 5. Дифференциальное исчисление функции нескольких переменных.
5.1. Найти дифференциал 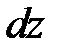 функции
функции 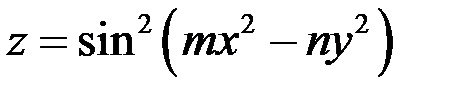 .
.
5.2. Показать, что функция 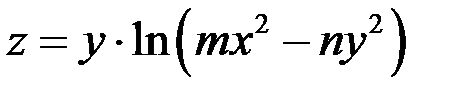 удовлетворяет уравнению
удовлетворяет уравнению 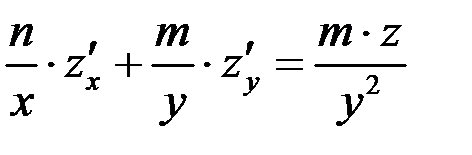 .
.
5.3. Составить уравнения касательной плоскости и нормали к поверхности 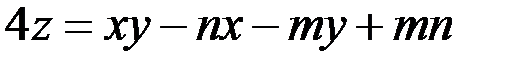 в точке
в точке 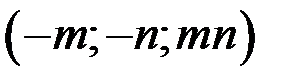 .
.
5.4. Для функции 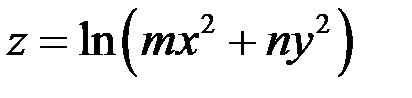 в точке
в точке 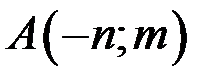 найти градиент и производную по направлению
найти градиент и производную по направлению 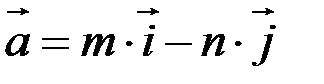 .
.
Краткие теоретические сведения для выполнения контрольной работы № 5 и решение типовых задач
Частные производные функции двух переменных
Переменная z называется функцией двух независимых переменных х и у на некотором множестве точек 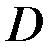 , если каждой паре значений
, если каждой паре значений 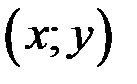 из множества
из множества 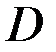 соответствует определенное значение величины z.
соответствует определенное значение величины z.
Пишут:
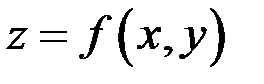 .
.
С геометрической точки зрения функция 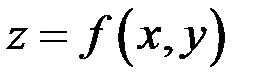 представляет собой поверхность.
представляет собой поверхность.
Если при 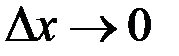 отношение частного приращения функции к вызвавшему его приращению аргумента
отношение частного приращения функции к вызвавшему его приращению аргумента 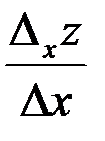 имеет конечный предел, то этот предел называется частной производной функции
имеет конечный предел, то этот предел называется частной производной функции 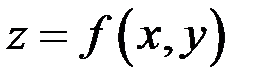 по независимой переменной х в точке
по независимой переменной х в точке 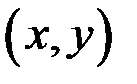 и обозначается
и обозначается 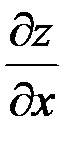 , или
, или 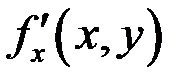 , или
, или 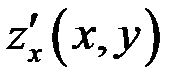 .
.
Таким образом, по определению
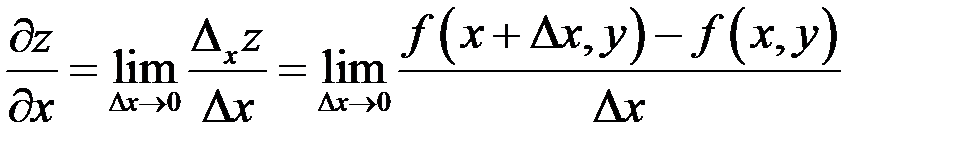 .
.
Аналогично,
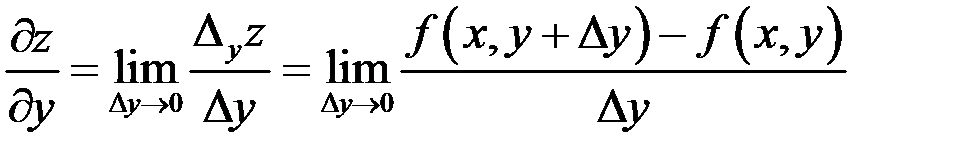 .
.
Так как 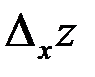 вычисляется при неизменном значении переменной у, а
вычисляется при неизменном значении переменной у, а 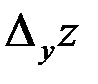 – при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции
– при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции 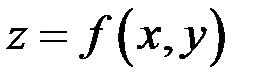 называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции
называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции 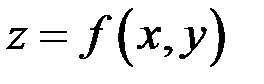 называется ее производная по у, вычисленная в предположении, что х – постоянная.
называется ее производная по у, вычисленная в предположении, что х – постоянная.
Пример 1
Найти частные производные функции 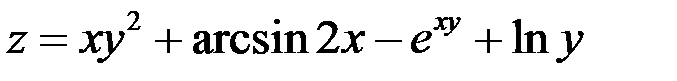 .
.
Решение
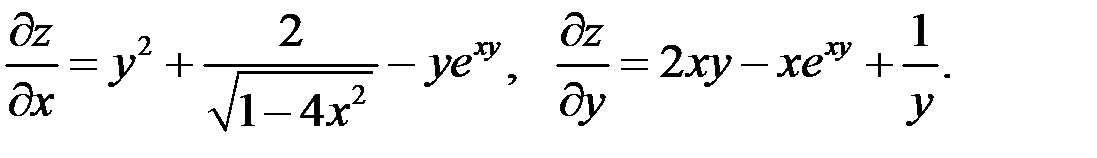
Пример 2
Показать, что функция 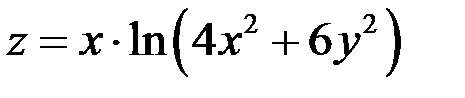 удовлетворяет уравнению
удовлетворяет уравнению 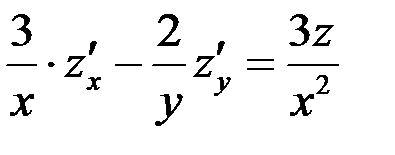 .
.
Решение
Найдем частные производные
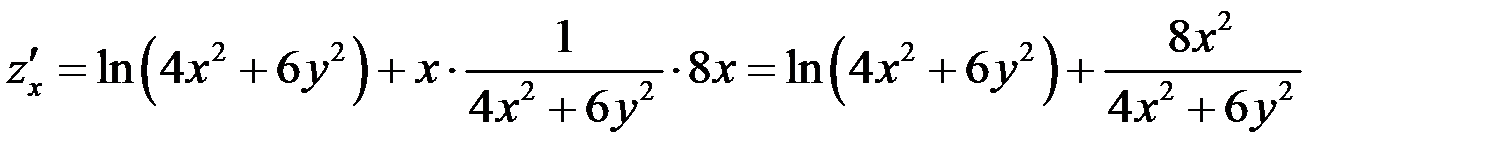 ,
,
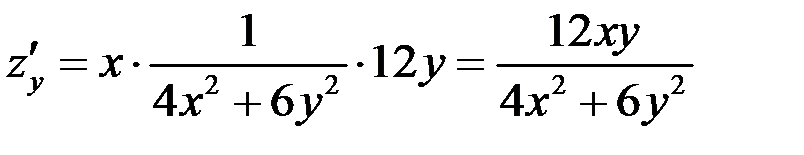 .
.
Подставим найденные выражения в левую часть уравнения:
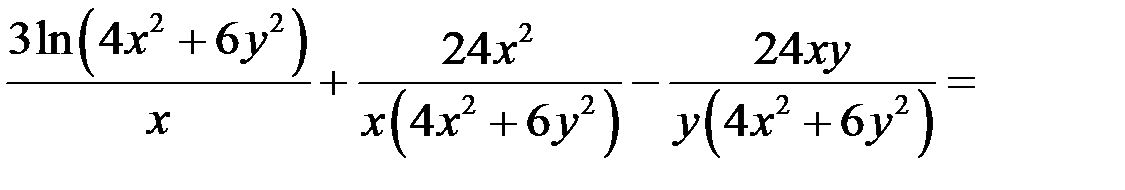
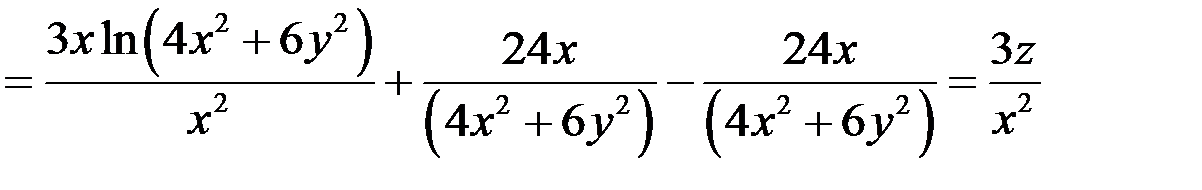 что и требовалось доказать.
что и требовалось доказать.
Дата: 2019-02-02, просмотров: 378.