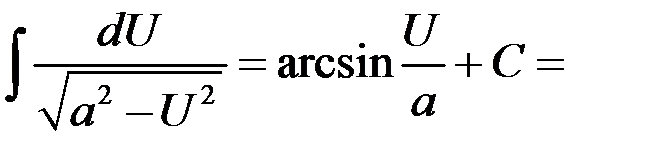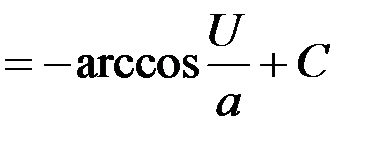Кафедра «Прикладная информатика и математика»
МАТЕМАТИКА
Методические указания
по контрольным работам для студентов
заочного отделения
Санкт-Петербург
2015
Одобрено на заседании кафедры «Прикладная информатика и математика»
протокол № ___ от ________ 2015 г.
Сборник заданий по математике. Методические указания по выполнению контрольных работ по курсу «Математика » для студентов заочного отделения.
Сборник содержит задачи контрольных работ по математике для студентов заочного отделения всех направлений, предусмотренные учебной программой в соответствии с ФГОС ВО. Задания и методические указания могут быть использованы в курсах математических дисциплин всех направлений и специальностей СПб УУиЭ.
Составитель:
к.п.н., доцент С.Д. Прозоровская
к.э.н. Т.А. Черняк
Рецензент:
Санкт-Петербургский университет управления и экономики
2015
ОГЛАВЛЕНИЕ
1. Требования к оформлению контрольных работ………..……..….…4
2. Формирование исходных данных к задачам………………….…..…4
3. Рекомендуемая литература…………………….……………………..5
4. Контрольная работа № 1. Линейная алгебра……………………..…6
5. Контрольная работа № 2. Элементы векторной алгебры и аналитической геометрии……………………………………………………24
6. Контрольная работа № 3. Предел и производная функции одной переменной……………………………………………………….….35
7. Контрольная работа № 4. Интегральное исчисление функции одной переменной…………………………………………………..….50
8. Контрольная работа № 5 Дифференциальное исчисление функции нескольких переменных……………………………………………57
9. Краткое содержание (программа) курса…………………….…….63
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в отдельной тетради. На обложке тетради необходимо указать: название института Университета; название кафедры; название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и личный шифр студента.
2. На каждой странице следует оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номера задач по данному сборнику. В условия задач следует сначала подставить конкретные числовые значения параметров т и п, после чего выполняется их решение.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Контрольная работа № 1. Элементы линейной алгебры
1.1. Найти значение матричного многочлена 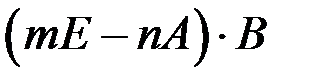 , если
, если 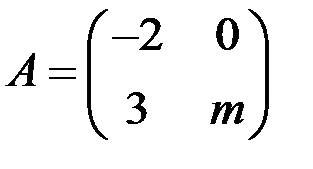 ,
, 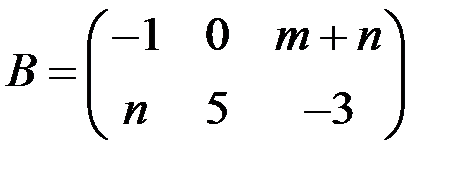 ,
, 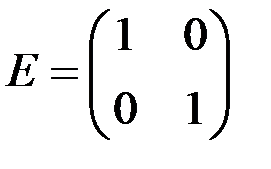 .
.
1.2. Вычислить определитель двумя способами, по правилу треугольника и разложением по строке (или столбцу): 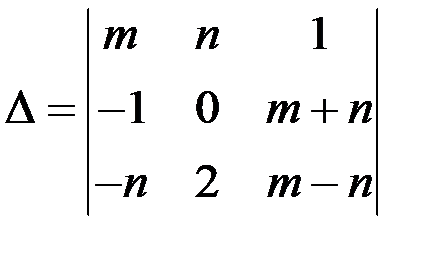 .
.
1.3. Найти матрицу обратную к матрице 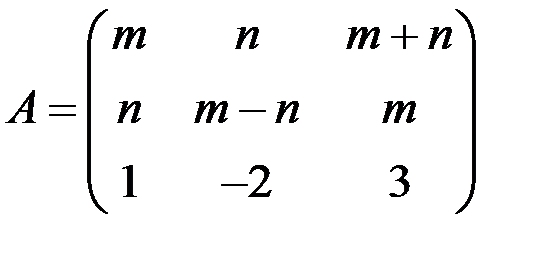 и проверить выполнение равенства
и проверить выполнение равенства 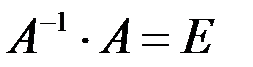 .
.
1.4. Решить систему линейных алгебраических уравнений двумя способами: по формулам Крамера и методом Гаусса: 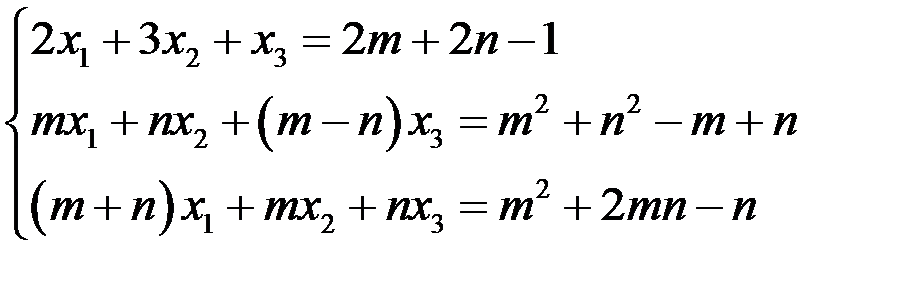 .
.
Матрицы и действия над ними
Прямоугольная таблица чисел вида
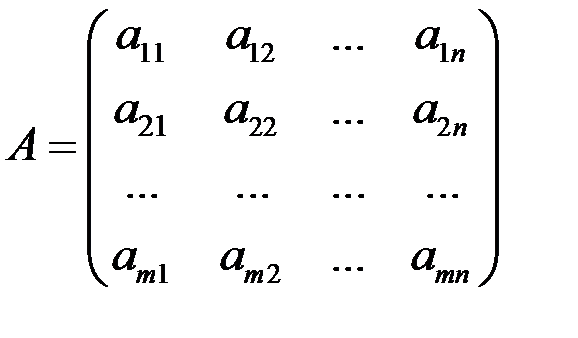
называется матрицей размера m ´ n; здесь m – число строк, n – число столбцов.
Числа 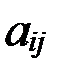 (i = 1,2,…,m; j = 1,2,…,n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.
(i = 1,2,…,m; j = 1,2,…,n) составляющие матрицу, называются ее элементами. Первый индекс i означает номер строки, второй j – номер столбца.
Если число строк и столбцов матрицы одинаковое 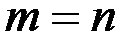 , то матрица называется квадратной, порядка n.
, то матрица называется квадратной, порядка n.
Квадратная матрица, в которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной, а диагональная матрица, у которой все элементы, стоящие на главной диагонали равны единице, называется единичной:

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю. Например:
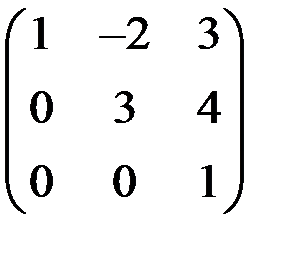 .
.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается символом О, например 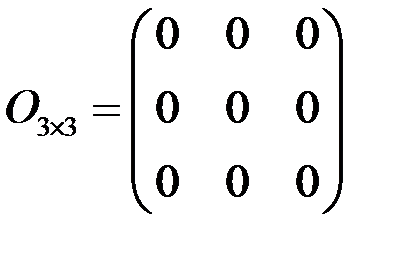 .
.
Прямоугольная матрица, в которой каждая строка заменена столбцом с тем же номером, называется транспонированной по отношению к данной матрице, обозначается 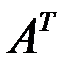 . Например, если
. Например, если 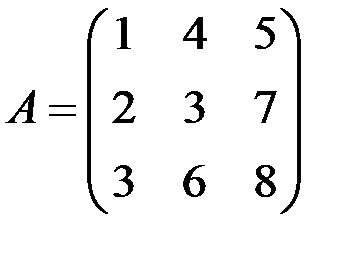 , то
, то 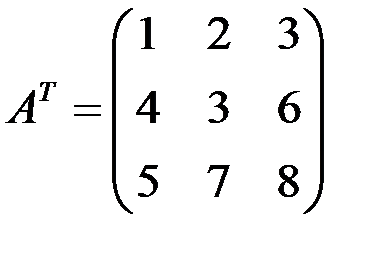 .
.
Очевидно, что 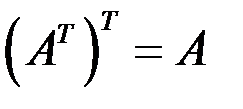 .
.
Действия над матрицами
Две матрицы одинакового размера называются равными, если их соответствующие элементы равны.
А = В, если 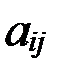 =
= 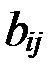 (i = 1,2,…,m; j = 1,2,…,n).
(i = 1,2,…,m; j = 1,2,…,n).
Суммой двух матриц одинакового размера называется матрица того же размера, все элементы которой равны суммам соответствующих элементов слагаемых матриц.
А + В = С, если 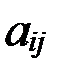 +
+ 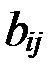 =
= 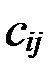 (i = 1,2,…,m; j = 1,2,…,n).
(i = 1,2,…,m; j = 1,2,…,n).
Пример 1
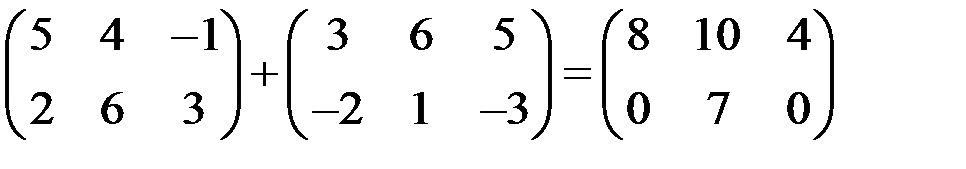 .
.
Произведением матрицы А на число α называется матрица αА или Аα, все элементы которой равны соответствующим элементам матрицы А, умноженным на α.
Пример 2
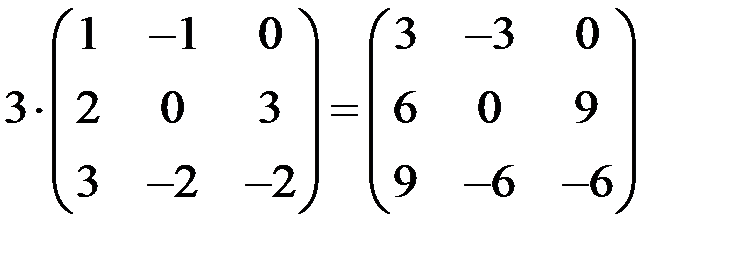
Матрица 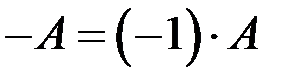 называется противоположной матрице А.
называется противоположной матрице А.
Умножение матриц.
Пусть дана матрица А размера m ´ n и матрица В размера n ´ p.
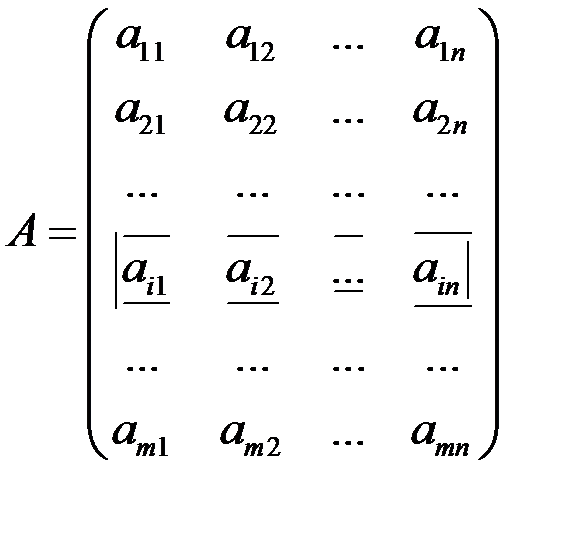
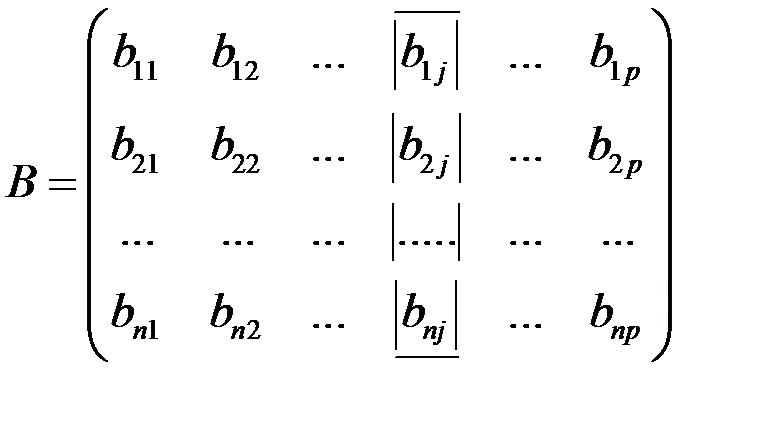
Для двух матриц А и В, у которых число столбцов первой матрицы равно числу строк второй матрицы, определено понятие произведения матрицы А на В следующим образом:
С = А · В , где С есть матрица размера m ´ p,
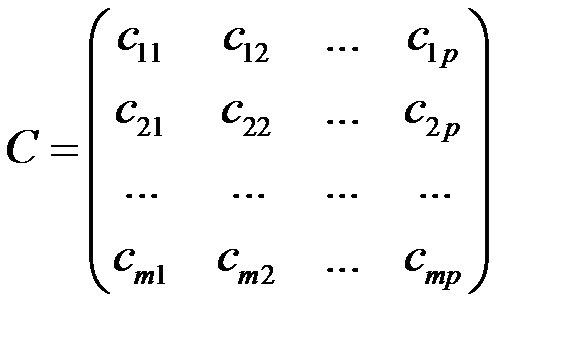
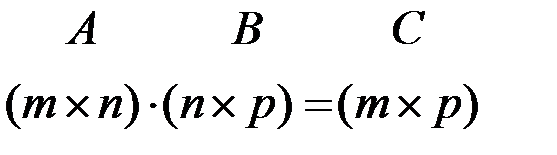 ,
,
если 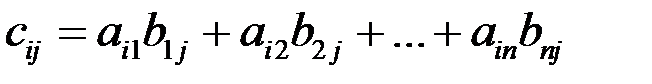 , где (i = 1,2,…,m; j = 1,2,…,p).
, где (i = 1,2,…,m; j = 1,2,…,p).
Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i-той строке и j-том столбце произведения двух матриц, нужно элементы i-той строки первой матрицы умножить на соответствующие элементы j–го столбца второй и полученные произведения сложить.
Таким образом, чтобы составить первую строку матрицы С нужно перемножить первую строку матрицы А поочередно на все столбцы В; чтобы получить вторую строку произведения С, нужно вторую строку А перемножить последовательно на все столбцы В и т.д.
Пример 3 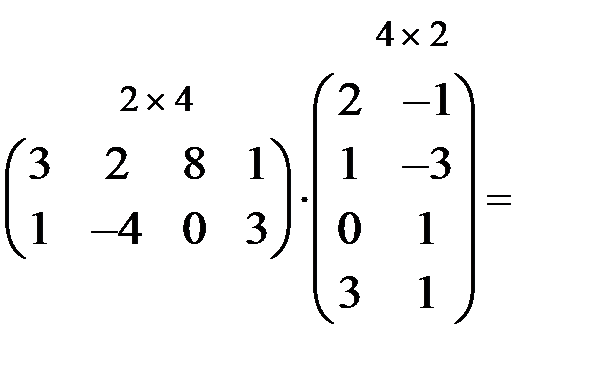
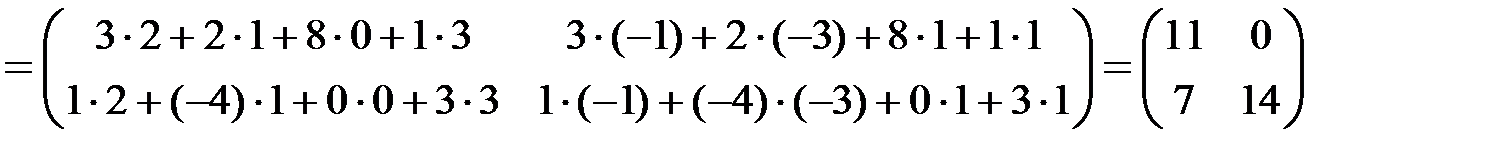
Произведение двух матриц НЕ подчиняется переместительному (коммутативному) закону
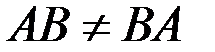 ,
,
в чем можно убедиться на примерах. Кроме того, если произведение АВ определено, то ВА может не иметь смысла.
В частных случаях, когда 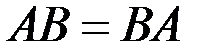 матрицы называются перестановочными.
матрицы называются перестановочными.
Легко доказать, что единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем
А Е = Е А = А.
Таким образом, единичная матрица играет роль единицы при умножении.
Пример 4
Найти значение матричного многочлена 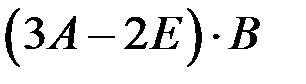 , если
, если 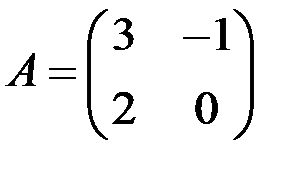 ,
, 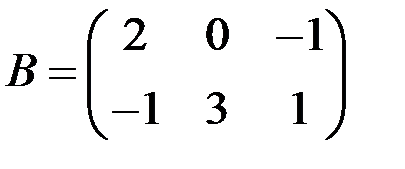 ,
, 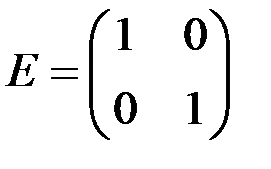 .
.
Решение
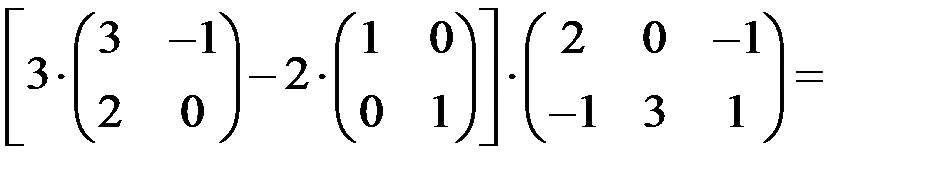
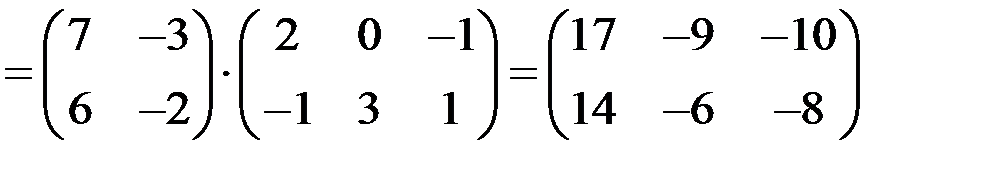 .
.
Пример 3
Вычислить определитель по правилу треугольника: 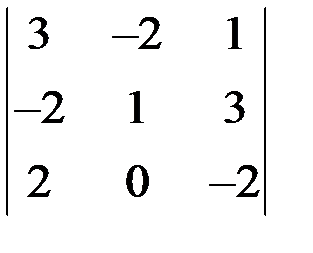 .
.
Решение
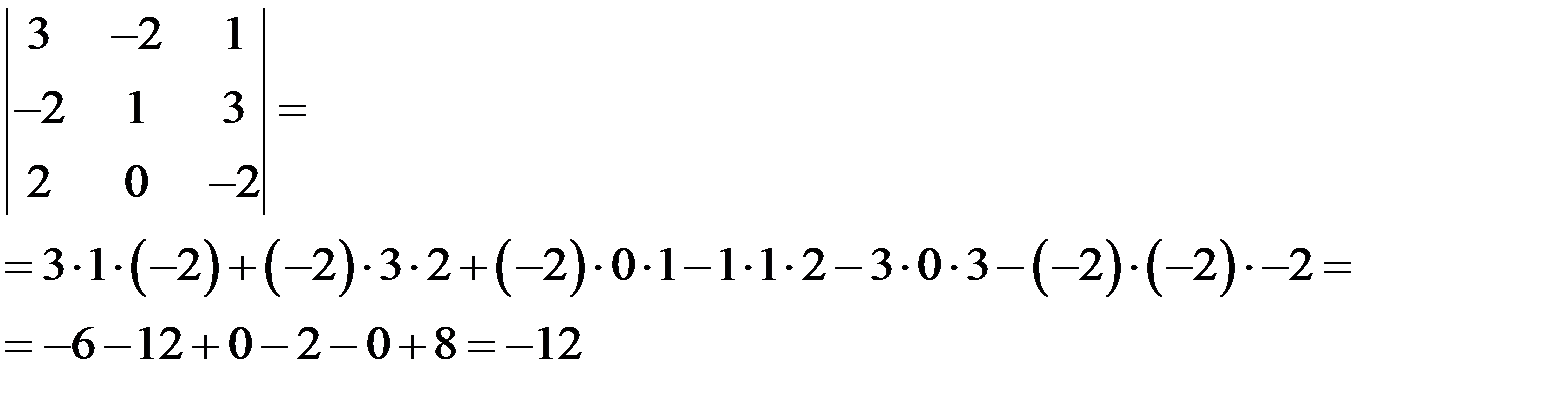
Свойства определителей
Рассмотрим свойства определителей на примере определителя 3-го порядка.
Рассмотрим определитель:
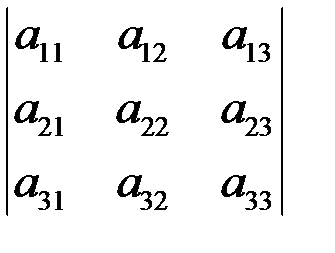 .
.
Определение. Минором некоторого элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пресечении которых стоит этот элемент. Обозначение минора 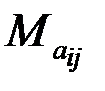 .
.
Пример 4
Минор элемента а12: 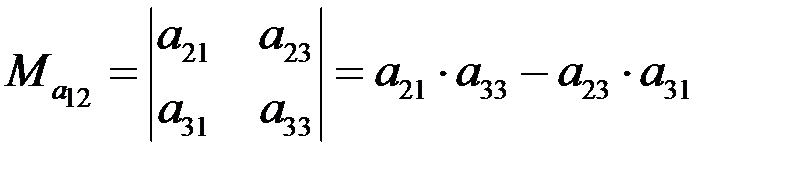 .
.
Определение. Алгебраическим дополнением любого элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, есть число четное, либо с противоположным знаком, если эта сумма есть число нечетное. Обозначение алгебраического дополнения А ij.
Пример 5
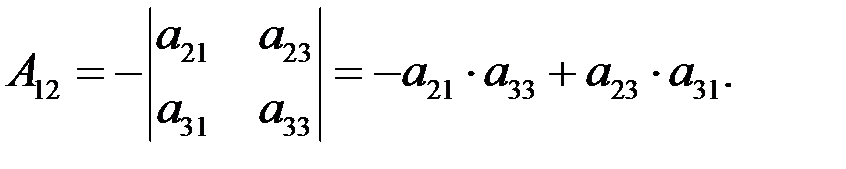
Свойство 1. Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.
Пример 6
Вычислим определитель, разложив его по элементам 1-ой строки:
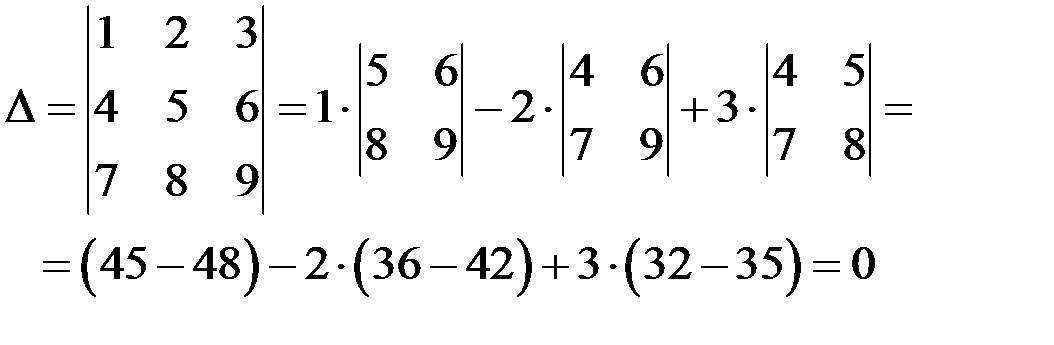 .
.
Свойство 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.
Свойство 3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).
Свойство 4. Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя.
Свойство 5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю.
Свойство 6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю.
Свойство 7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.
Свойство 8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые:
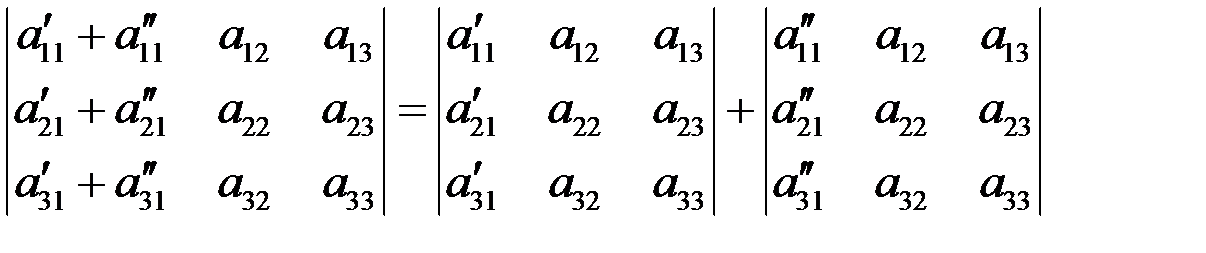 .
.
Свойство 9. Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится.
Пример 7
Вычислим определитель:
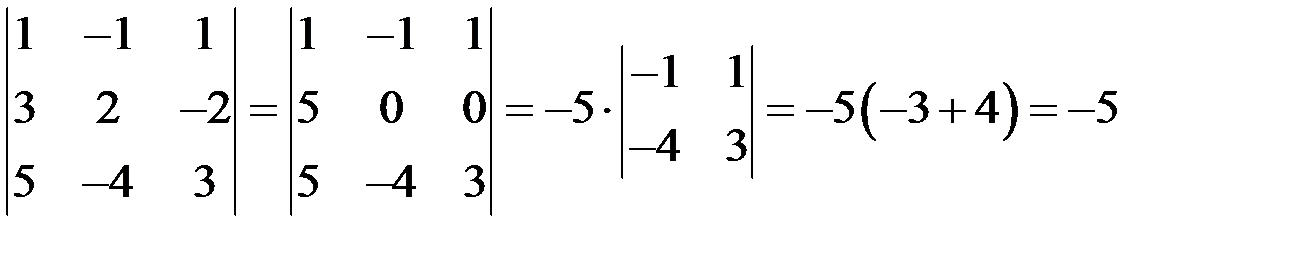 ,
,
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица 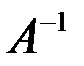 , которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
По определению
А · 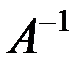 =
= 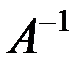 · А = Е.
· А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
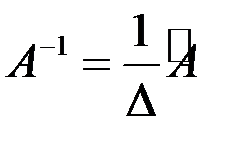 ,
,
где 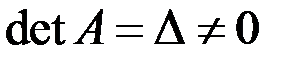 - определитель матрицы А,
- определитель матрицы А, 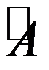 - союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
- союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
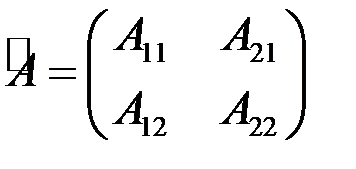 ,
,
для квадратной матрицы 3-го порядка союзной является матрица
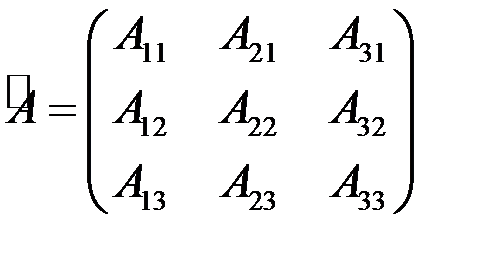 .
.
Пример
Для матрицы 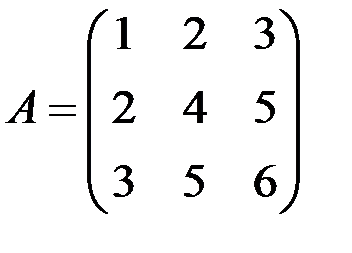 найти обратную.
найти обратную.
Решение
Обратную матрицу находим по формуле
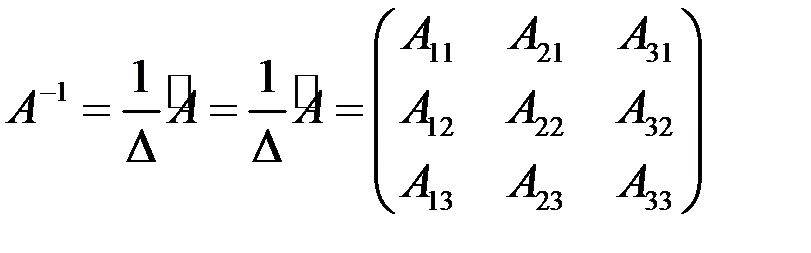 .
.
Определитель матрицы 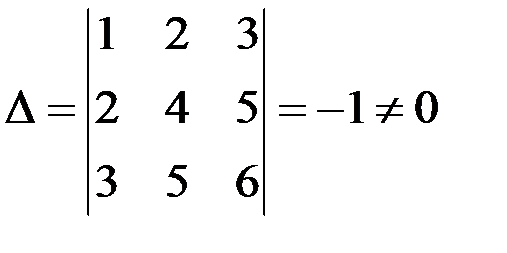 , следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
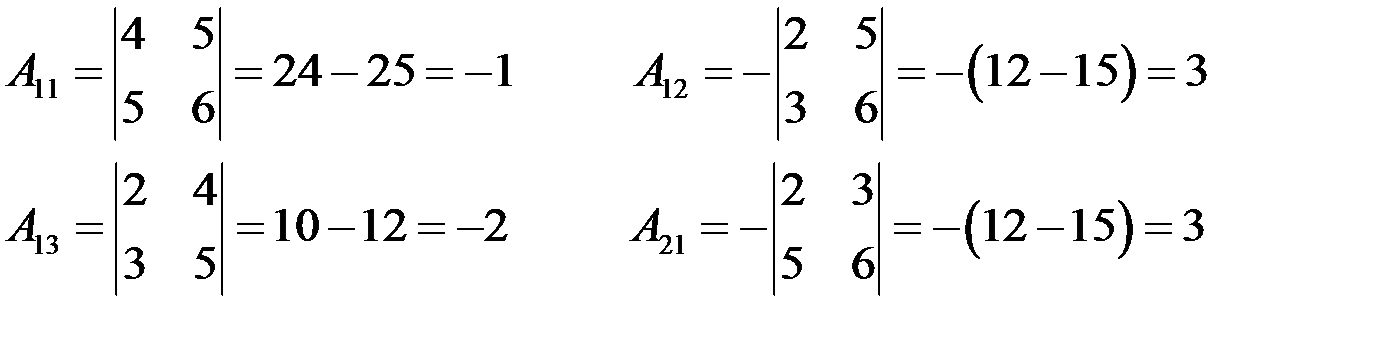
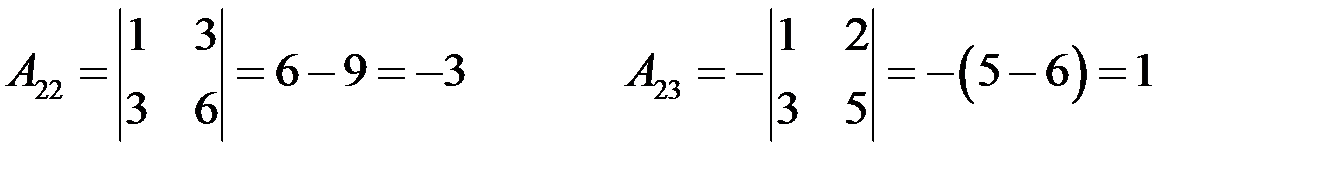
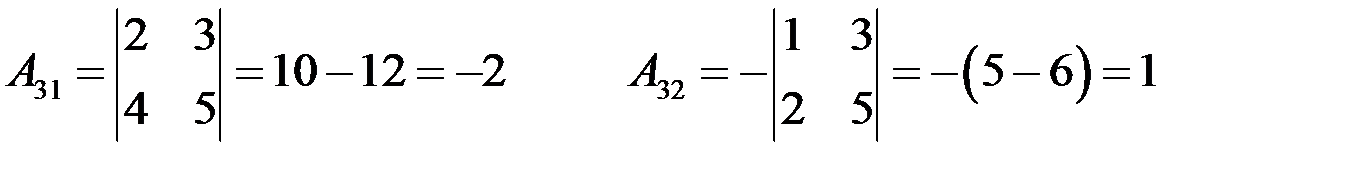
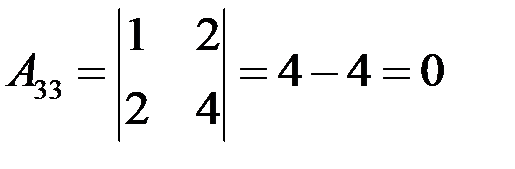 .
.
Тогда обратная матрица имеет вид
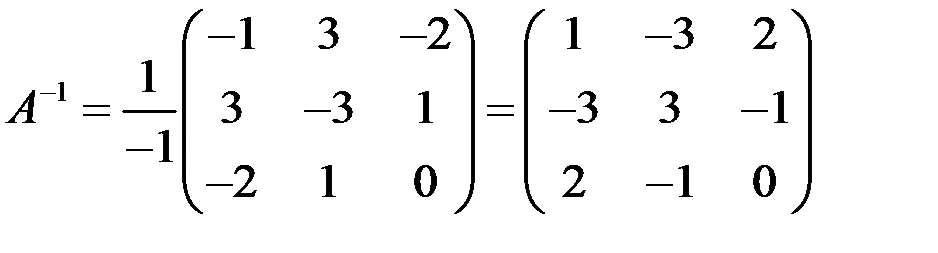 .
.
Решение
Формулы Крамера: 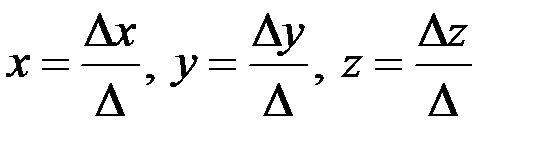 . Вычислим определители:
. Вычислим определители:
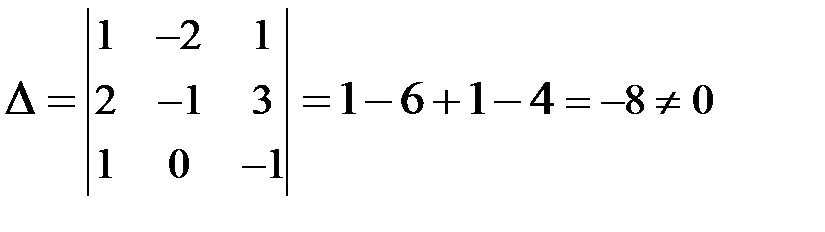 ,
,
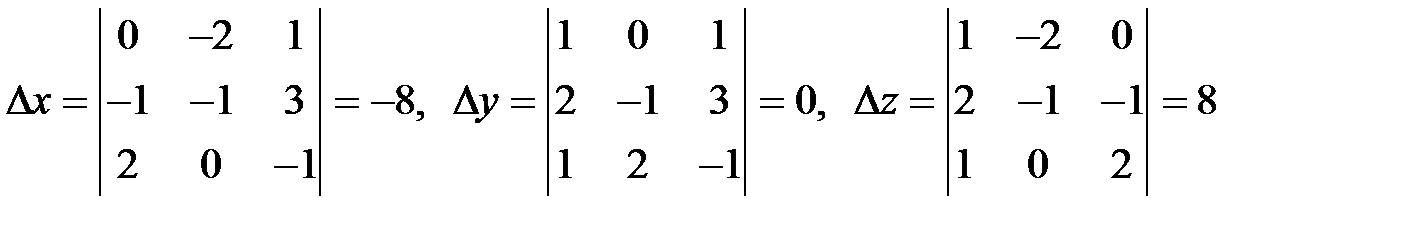 , тогда
, тогда
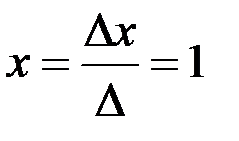 ,
, 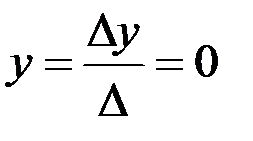 ,
, 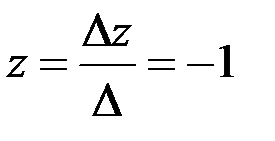 .
.
Итак, 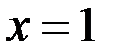 ,
, 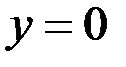 ,
, 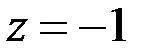 .
.
Ранг матрицы
Пусть дана матрица 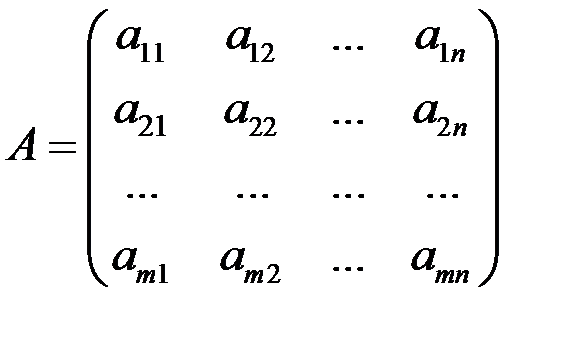 .
.
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Обозначение: rang A, r(А) или r.
Очевидно, 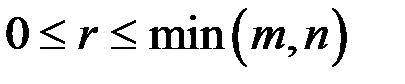 – меньшее из чисел m и n.
– меньшее из чисел m и n.
Минор, порядок которого определяет ранг матрицы, называется базисным. Вычисление всех миноров отличных от нуля трудоемкая операция. На практике для вычисления r(A) используют метод Гаусса.
Элементарными преобразованиями называются следующие действия над матрицами:
1. Вычеркивание нулевой строки.
2. Умножение какой либо строки на число.
3. Прибавление к одной из строк другой строки, умноженной на любое число.
4. Перестановка двух столбцов или двух строк.
Теорема 1. Ранг матрицы не меняется при элементарных преобразованиях.
Пример 2.
Найти ранг матрицы 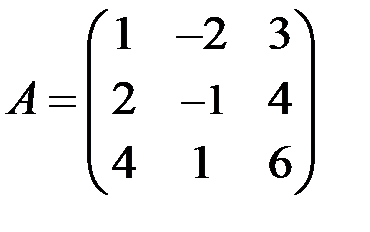 .
.
Решение
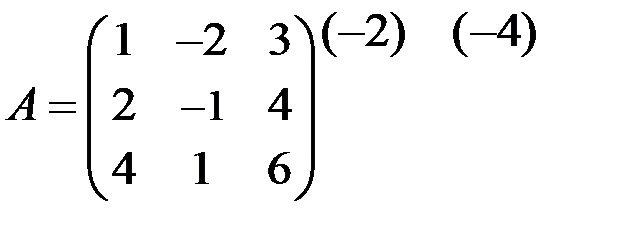 ~
~ 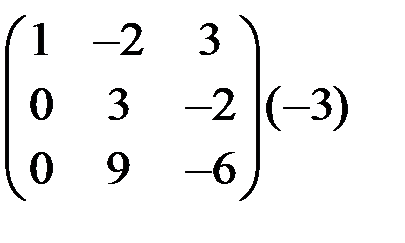 ~
~ 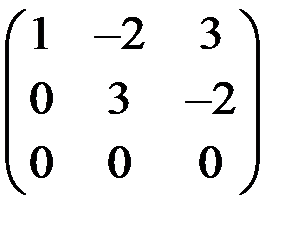
На первом шаге первую строку матрицы умножили на (-2) и сложили со второй строкой, умножили первую строку на (-4) и сложили с третьей строкой. На втором шаге вторую строку умножили на (-3) и сложили с третьей строкой. Нулевую строку вычеркнули. Таким образом, ранг матрицы r = 2.
Метод Гаусса решения СЛАУр
Пусть дана система линейных алгебраических уравнений (СЛАУр)
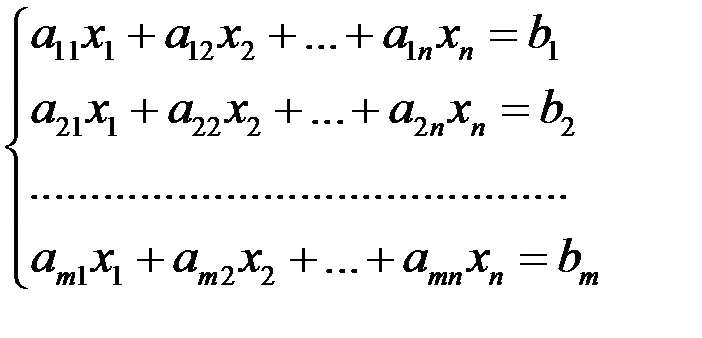
Поставим задачу: исследовать данную систему, т.е. выяснить, не решая ее, совместна она или несовместна, а если совместна, то определенна она или неопределенна.
На все эти вопросы отвечает теорема Кронекера - Капелли.
Пусть дана матрица системы 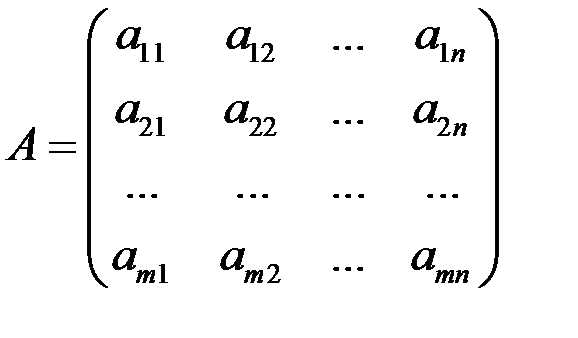 .
.
Рассмотрим расширенную матрицу системы
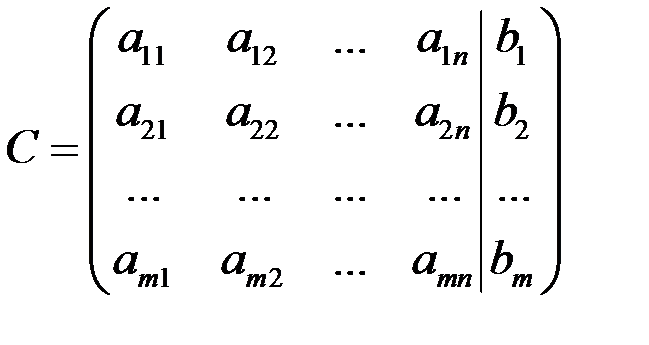 .
.
Теорема Кронекера – Капелли.
СЛАУр совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы:
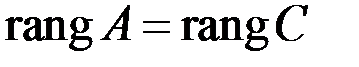 или
или 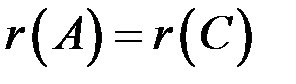 .
.
Замечание
Если 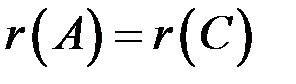 и
и 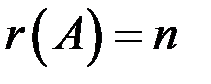 , где n – число неизвестных, то система определенна; если
, где n – число неизвестных, то система определенна; если 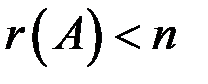 , то система неопределенна, если же
, то система неопределенна, если же 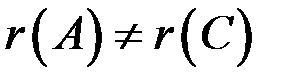 , то система несовместна.
, то система несовместна.
Метод Гаусса решения СЛАУр состоит в следующем.
1. Выписывают расширенную матрицу системы
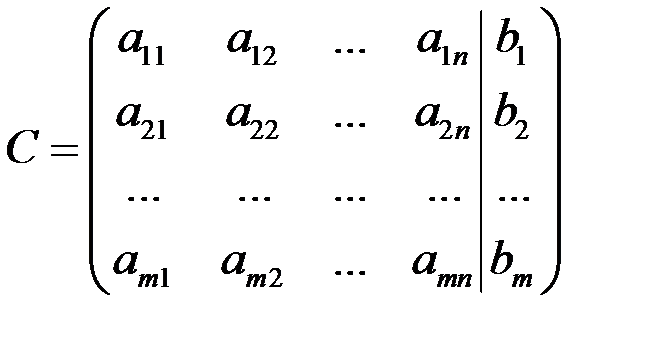
и с помощью элементарных преобразований приводят ее к трапециевидному виду.
2. Применяя теорему Кронекера – Капелли, исследуют систему, получая один из случаев:
– система совместна и определенна,
– система совместна и неопределенна,
– система несовместна.
Трапециевидная форма расширенной матрицы С в каждом из этих случаев имеет вид:
1) С ~ 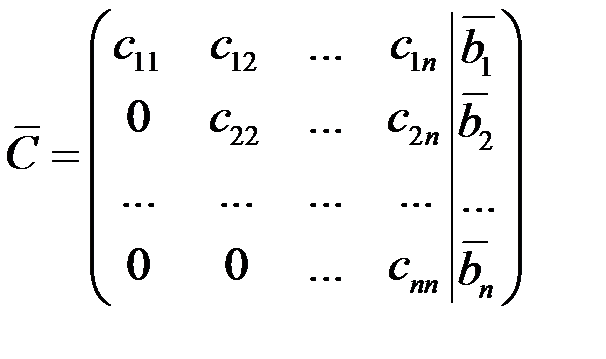
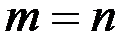 ,
, 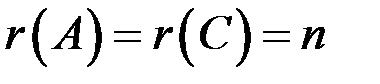 ,
,
следовательно, система определенна, имеет единственное решение,
2) С ~ 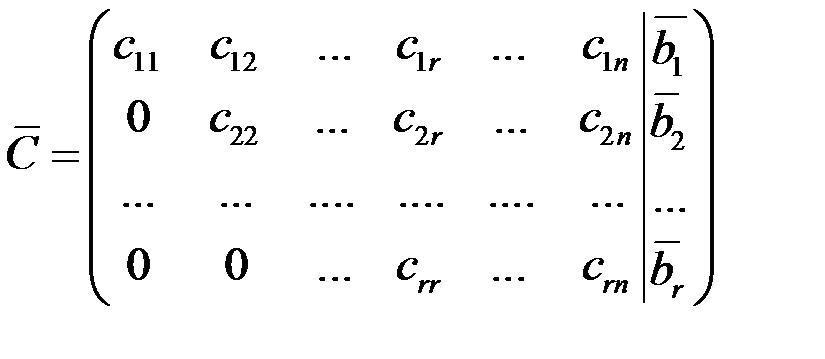
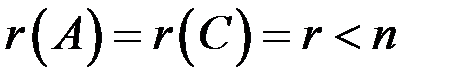 ,
,
следовательно, система неопределенна, имеет бесконечное множество решений,
3) если какая-либо строка матрицы С имеет вид 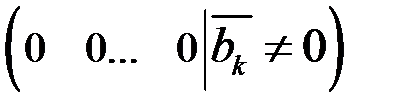 , то система несовместна (решений нет).
, то система несовместна (решений нет).
3. Для решения системы, если оно существует, следует записать новую систему, отвечающую полученной трапециевидной матрице, которая является более простой по сравнению с исходной и решить ее (обратный ход).
Пример 3.
Исследовать и решить СЛАУр: 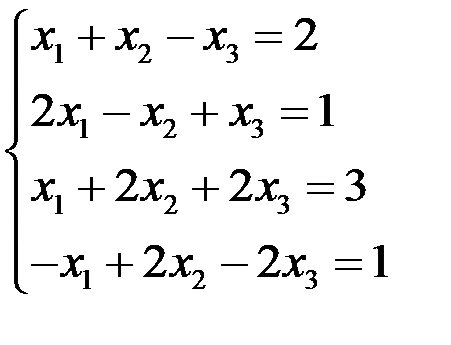 .
.
Решение
Составим расширенную матрицу и проведем над ней эквивалентные преобразования для определения 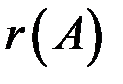 и
и 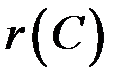 .
.
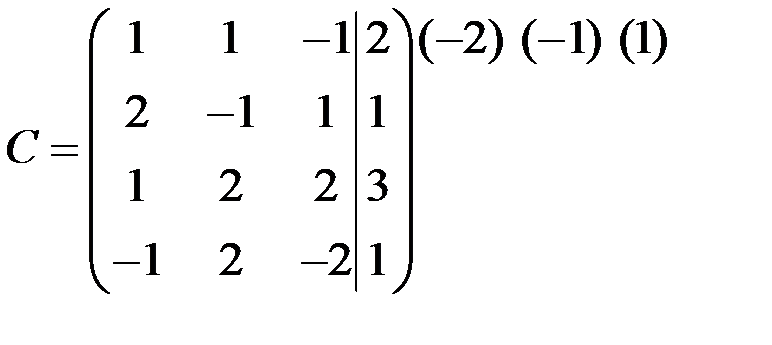 ~
~ 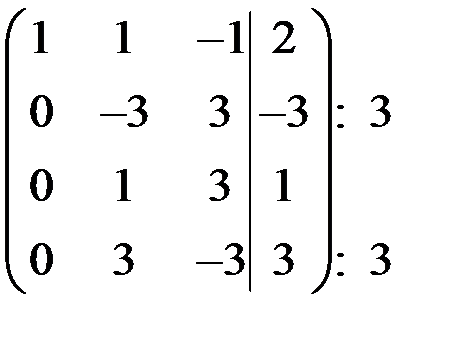 ~
~
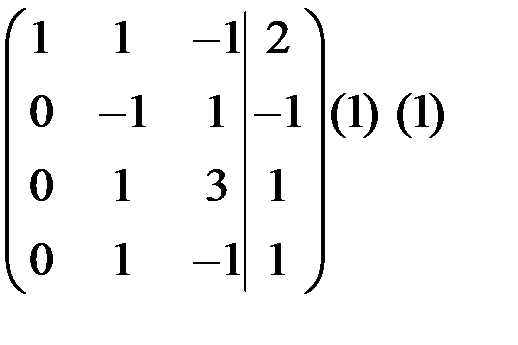 ~
~ 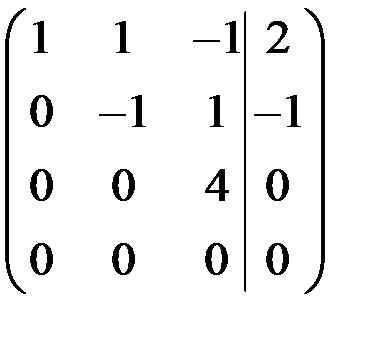 ,
,
Таким образом, 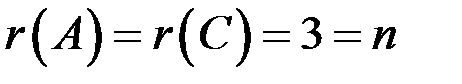 , следовательно, по теореме Кронекера – Капелли система совместна и определенна.
, следовательно, по теореме Кронекера – Капелли система совместна и определенна.
Составим систему, соответствующую последней матрице, эквивалентную исходной:
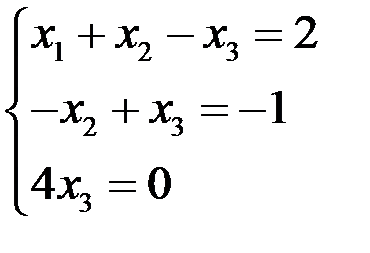 Þ
Þ 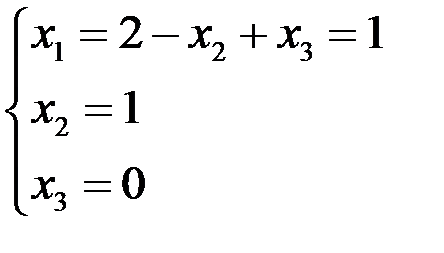 .
.
Таким образом, 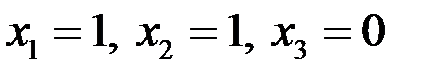 .
.
Пример 4.
Исследовать и решить СЛАУр: 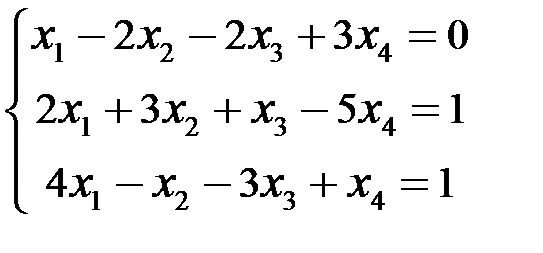 .
.
Решение
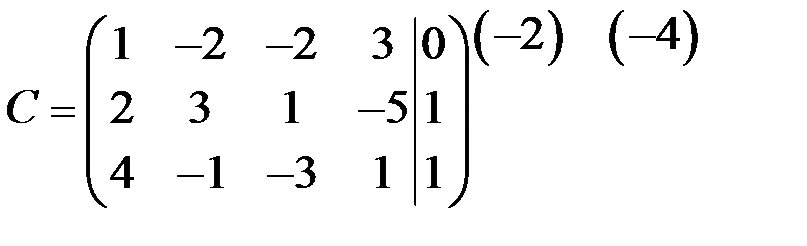 ~
~ 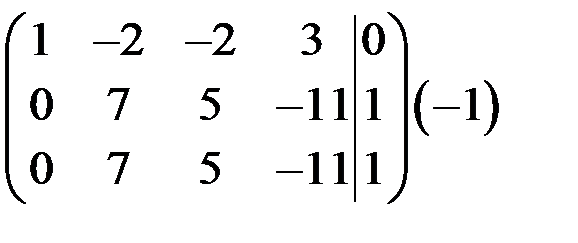 ~
~ 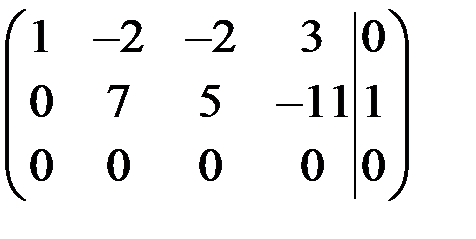
Так как 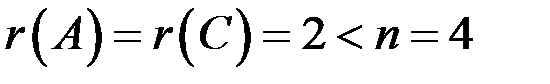 , следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
, следовательно, система совместна и неопределенна (имеет бесчисленное множество решений).
Последней матрице соответствует система:
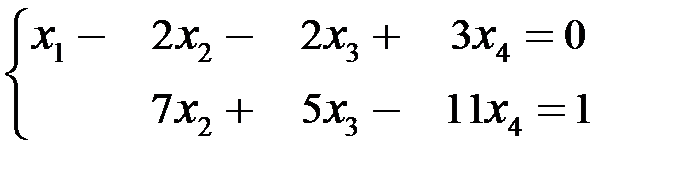 Þ
Þ 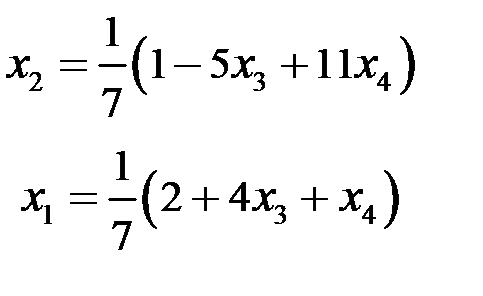
где 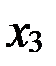 и
и 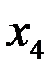 – произвольные параметры.
– произвольные параметры.
Пример 5.
Исследовать и решить СЛАУр: 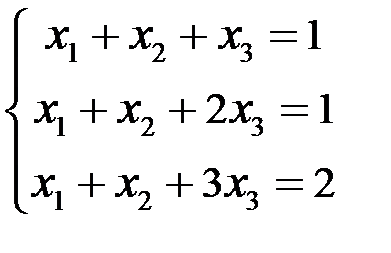
Решение
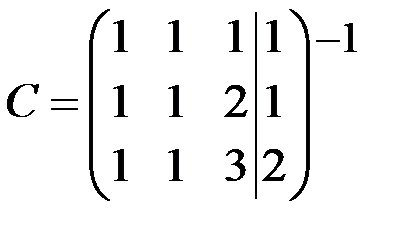 ~
~ 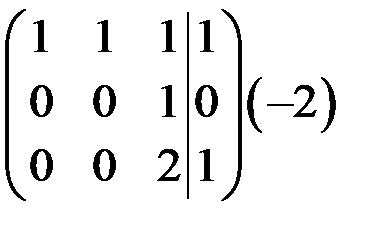 ~
~ 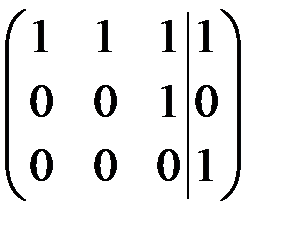
Так как 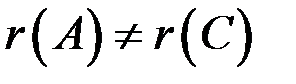 , то система несовместна (решений нет).
, то система несовместна (решений нет).
Пример 6.
Исследовать и решить СЛАУр: 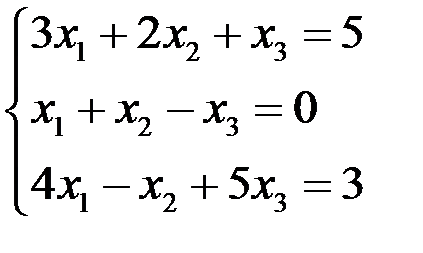 .
.
Решение
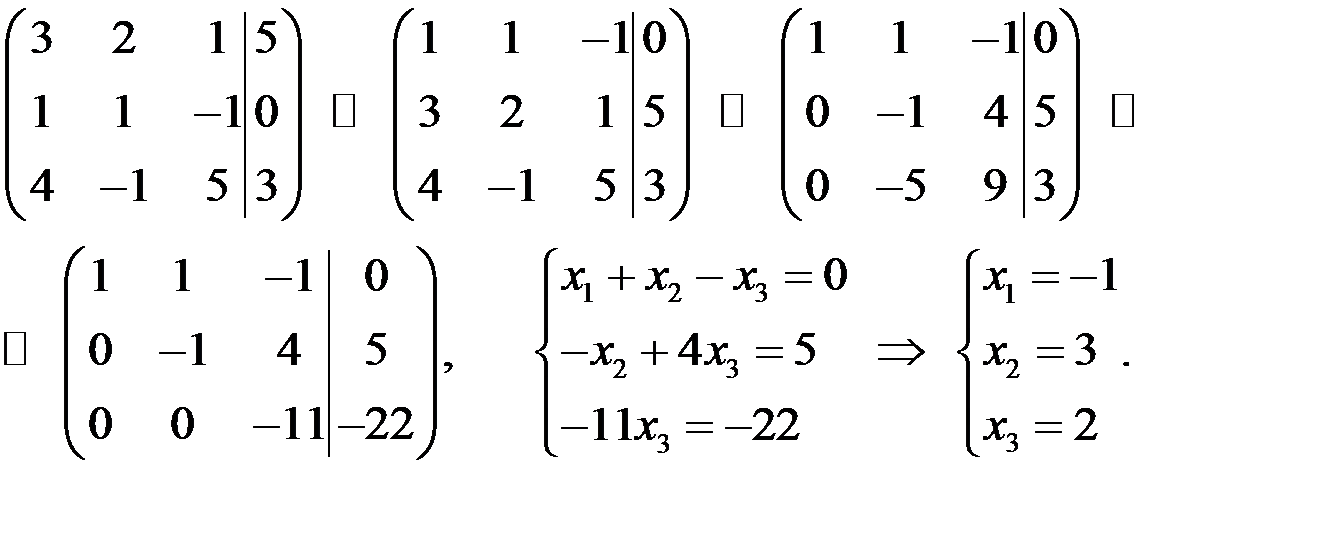
Таким образом, 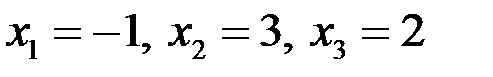 .
.
Прямая на плоскости
Уравнение вида
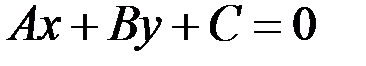
называется общим уравнением прямой.
Уравнение вида
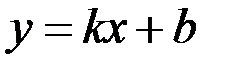
называется уравнением прямой с угловым коэффициентов, здесь 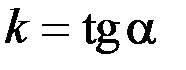 ,
, 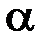 - угол, образованный прямой с положительным направлением оси Ох, b – ордината точки пересечения прямой с осью Оу.
- угол, образованный прямой с положительным направлением оси Ох, b – ордината точки пересечения прямой с осью Оу.
Пусть даны две точки прямой 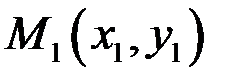 и
и 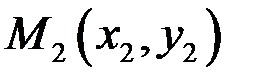 . Уравнение прямой, проходящей через две заданные точки имеет вид
. Уравнение прямой, проходящей через две заданные точки имеет вид
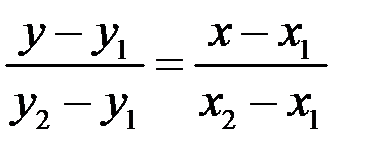 .
.
Уравнение прямой, проходящей через заданную точку 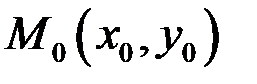 в заданном направлении, определяемом угловым коэффициентом k , имеет вид
в заданном направлении, определяемом угловым коэффициентом k , имеет вид
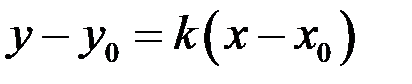 .
.
Пример
Даны вершины треугольника 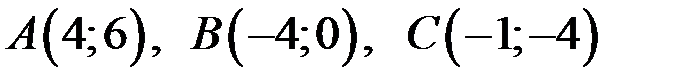 . Найти:
. Найти:
1) уравнение стороны АВ;
2) уравнение медианы, проведенной из вершины С;
3) координату точки пересечения медиан;
4) уравнение высоты, опущенной из вершины В на сторону АС и ее длину;
5) уравнение прямой, проходящей через точку С параллельно прямой АВ;
6) площадь треугольника.
Решение
1) Используем уравнение прямой, проходящей через две точки 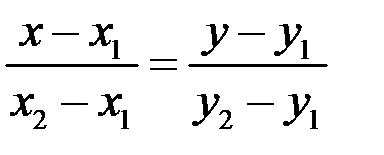 . Подставив координаты точек
. Подставив координаты точек 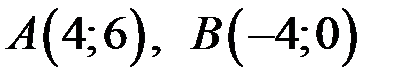 , получим
, получим
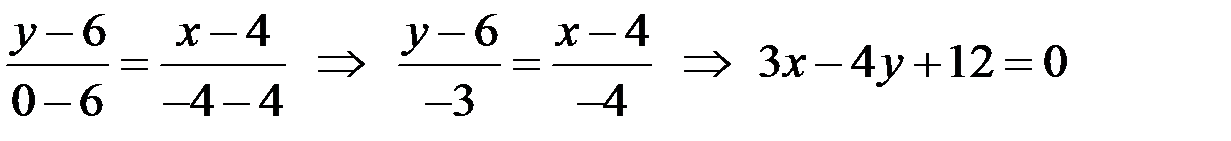 - общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом
- общее уравнение прямой АВ, из которого находим уравнение прямой с угловым коэффициентом 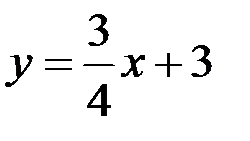 ,
, 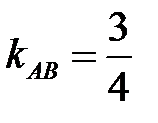 .
.
2) Медиана, проведенная из вершины С делит противолежащую сторону АВ треугольника пополам. Найдем координаты точки Е середины стороны 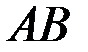 (рис.1):
(рис.1):
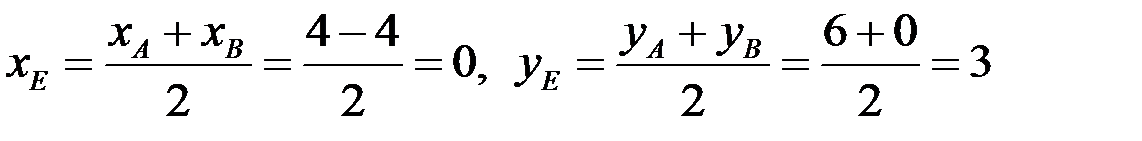 , т.е.
, т.е. 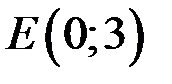 ,
, 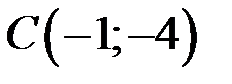 . Подставим координаты точек в уравнение прямой, проходящей через две точки, получим
. Подставим координаты точек в уравнение прямой, проходящей через две точки, получим 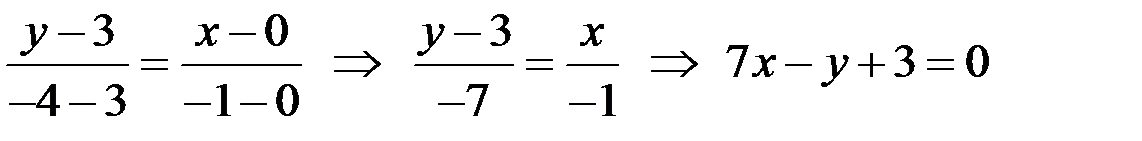 - общее уравнение прямой СЕ.
- общее уравнение прямой СЕ.
3) Точка М делит каждую медиану в отношении 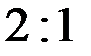 , считая от вершины. Таким образом, ее координаты
, считая от вершины. Таким образом, ее координаты 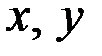 можно найти по формулам:
можно найти по формулам:
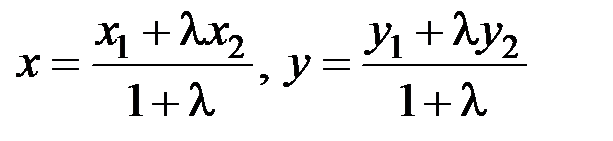 .
.
В нашем случае
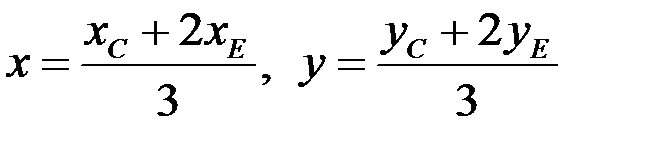 ,
,
откуда 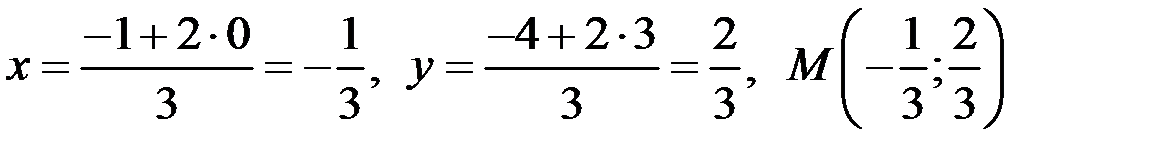 .
.
4) Найдем уравнение прямой, проходящей через заданную точку 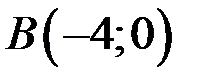 перпендикулярно прямой
перпендикулярно прямой 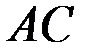 из уравнения
из уравнения 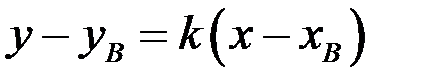 . Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки
. Найдем угловой коэффициент прямой АС, используя уравнение прямой, проходящей через две точки 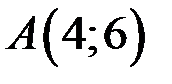 и
и 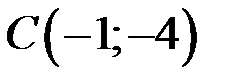 :
:
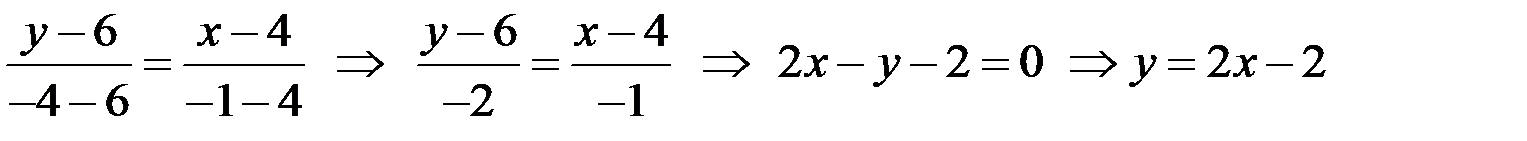 - уравнение АС.
- уравнение АС.
Угловой коэффициент прямой АС равен 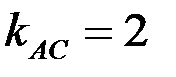 , тогда, используя условие перпендикулярности двух прямых
, тогда, используя условие перпендикулярности двух прямых 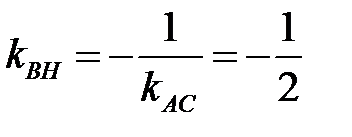 , получим
, получим
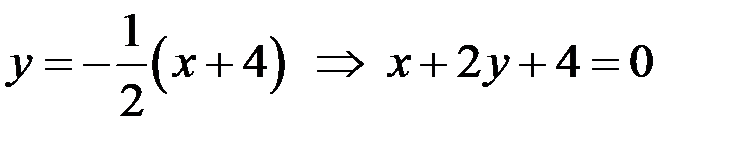 - уравнение высоты.
- уравнение высоты.
Длину высоты можно найти, как расстояние от точки 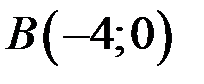 до прямой АС по формуле
до прямой АС по формуле 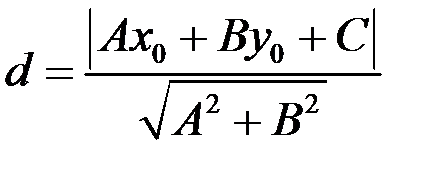 . В нашем случае уравнение прямой АС:
. В нашем случае уравнение прямой АС: 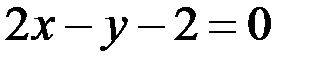 , следовательно,
, следовательно,
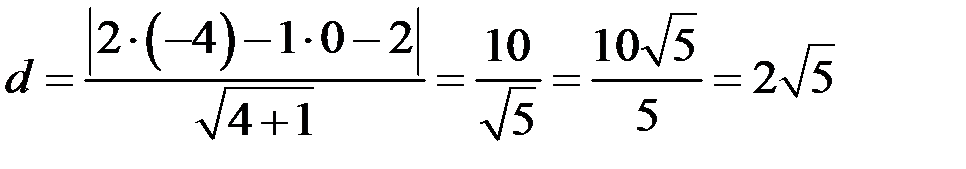 .
.
5) Для нахождения уравнения прямой, проходящей через точку С параллельно прямой АВ используем уравнение прямой, проходящей через заданную точку в заданном направлении 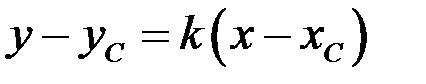 и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен
и условие параллельности двух прямых. Известно, что угловой коэффициент прямой АВ равен 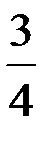 , следовательно,
, следовательно,
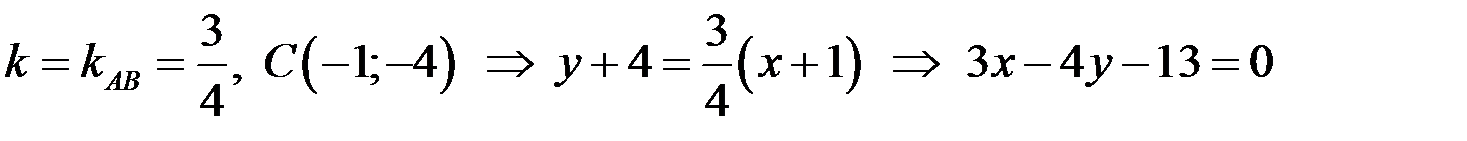 -
-
- уравнение искомой прямой.
6) Площадь треугольника находится по формуле: 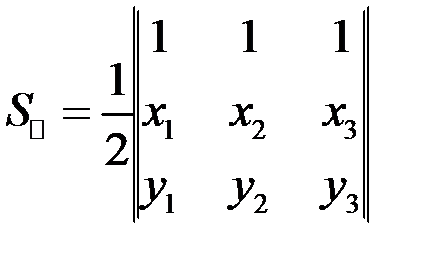 , в нашем случае
, в нашем случае
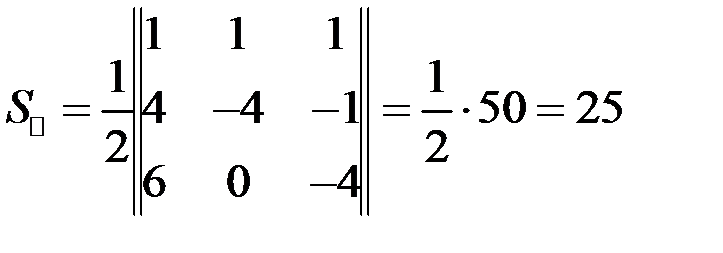 .
.
у А(4;6)
Е
В(-4;0) М
0 1 х
С(-1;-4)
Рис. 1
Пример
Даны вершины треугольной пирамиды 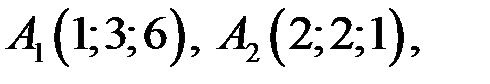
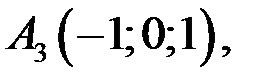
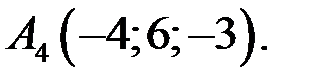 Найти:
Найти:
1) угол между ребрами 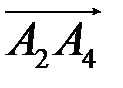 и
и 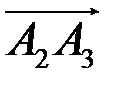 ;
;
2) площадь грани 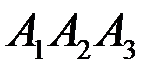 ;
;
3) объем пирамиды 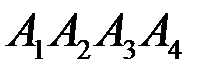 ;
;
4) длину высоты, опущенной из вершины 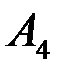 на грань
на грань 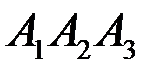 ;
;
5) угол между ребром 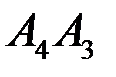 и гранью
и гранью 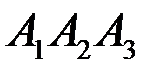 ;
;
6) уравнение высоты, опущенной из вершины 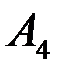 на грань
на грань 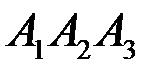 .
.
Решение
| А4 А2 В А1 А3 Рис. 2 | 1) Угол между ребрами 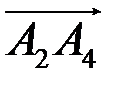 и и 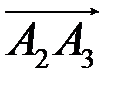 находим с помощью скалярного произведения векторов по формуле находим с помощью скалярного произведения векторов по формуле
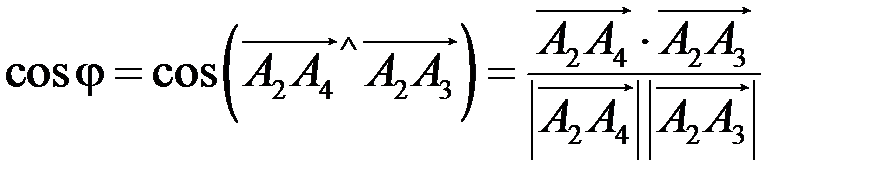 ,
найдем координаты векторов ,
найдем координаты векторов
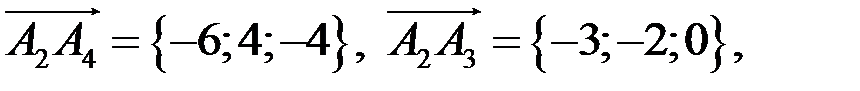 тогда косинус угла между векторами
тогда косинус угла между векторами
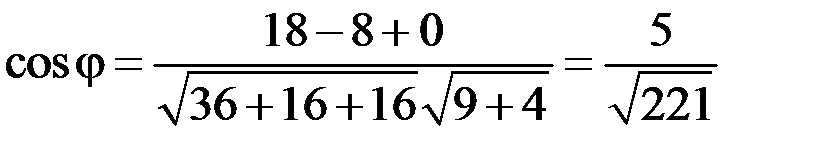 . .
|
2) Площадь грани 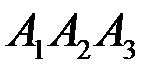 находим с помощью векторного произведения векторов. Найдем координаты вектора
находим с помощью векторного произведения векторов. Найдем координаты вектора 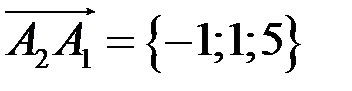 , тогда площадь треугольника находим по формуле
, тогда площадь треугольника находим по формуле
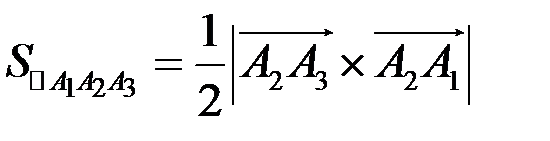 .
.
Найдем векторное произведение векторов
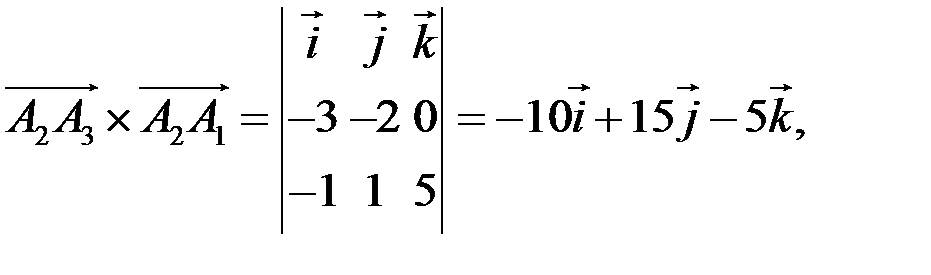
модуль векторного произведения равен
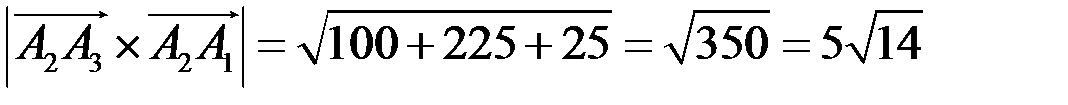 ,
,
откуда находим площадь треугольника
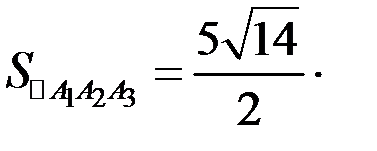
3) Объем пирамиды находим с помощью смешанного произведения векторов по формуле
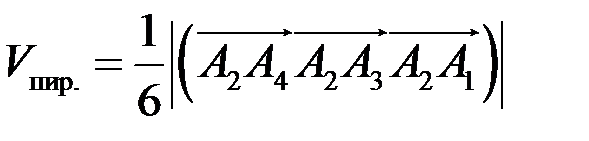 ,
,
так как выше найдены координаты векторов
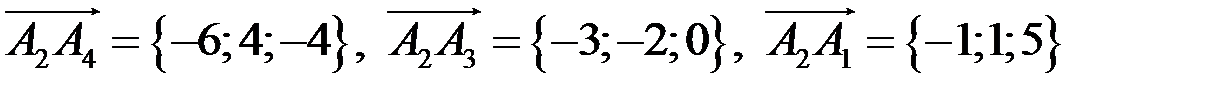 ,
,
подставим координаты векторов в формулу, получим
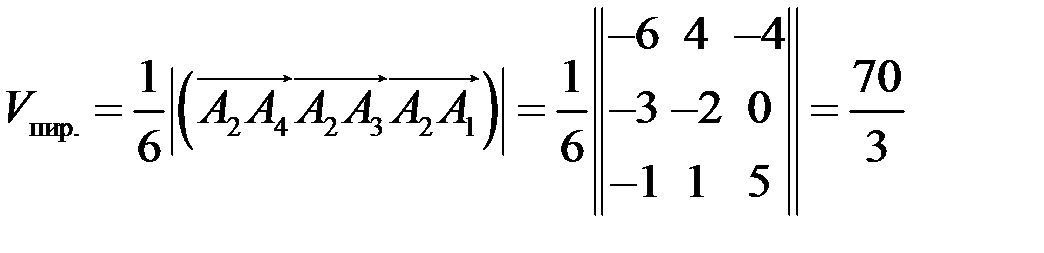 .
.
4) Для нахождения длины высоты h, опущенной из вершины 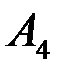 на грань
на грань 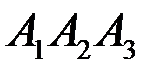 применим формулу
применим формулу
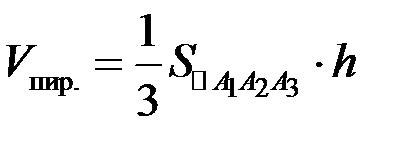 ,
,
откуда находим
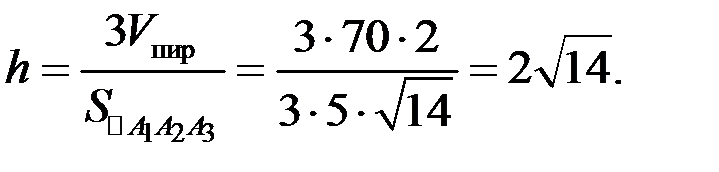
5) Общее уравнение плоскости 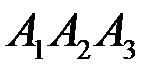 :
:
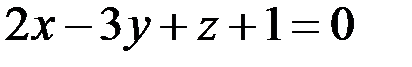 ,
,
нормальный вектор плоскости 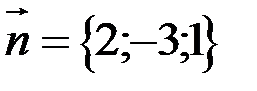 .
.
Уравнение высоты 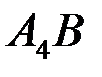 :
: 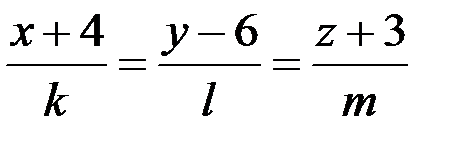 .
.
Условие перпендикулярности прямой и плоскости: 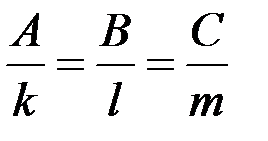 .
.
В нашем случае 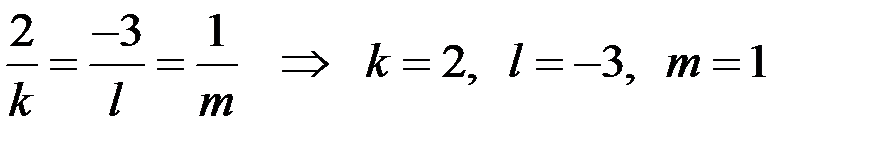 , тогда уравнение высоты имеет вид
, тогда уравнение высоты имеет вид
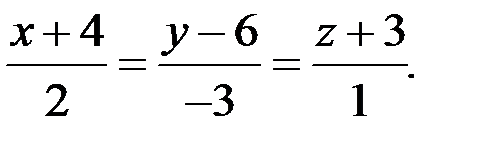
Пример 1
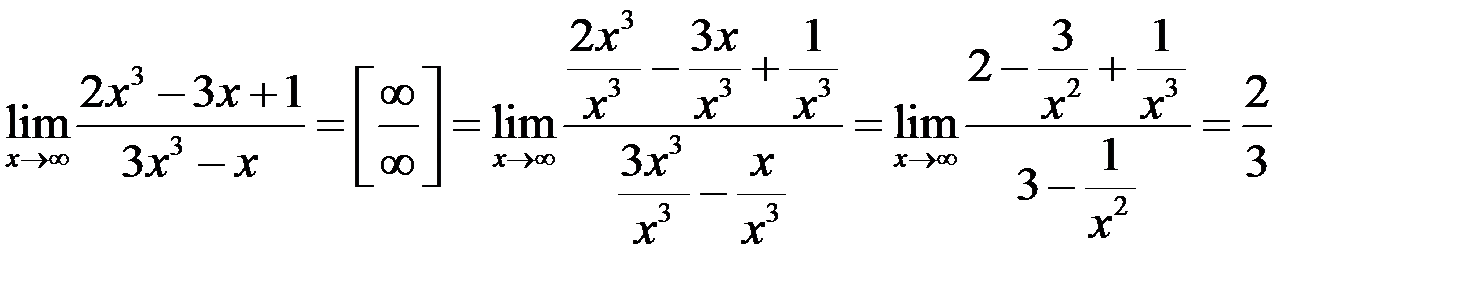 ,
,
так как при 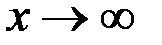 каждая из дробей
каждая из дробей 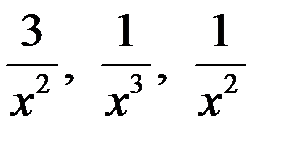 стремится к нулю.
стремится к нулю.
Пример 2
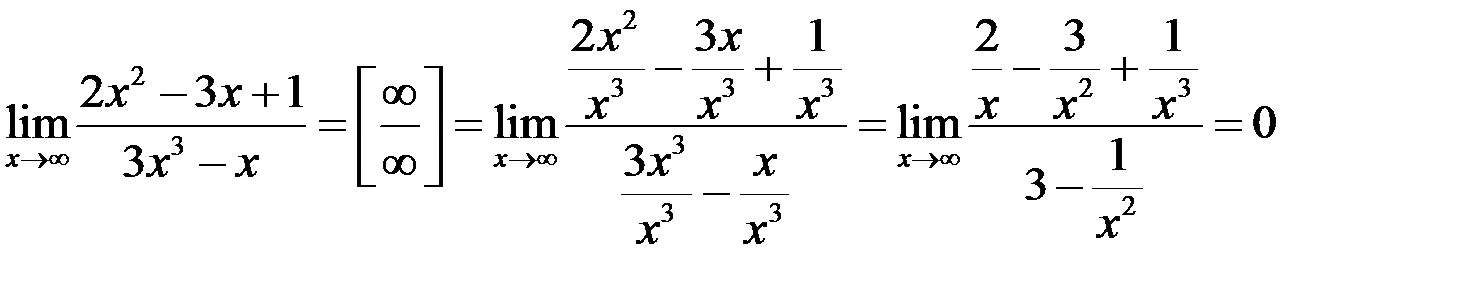 .
.
Пример 3
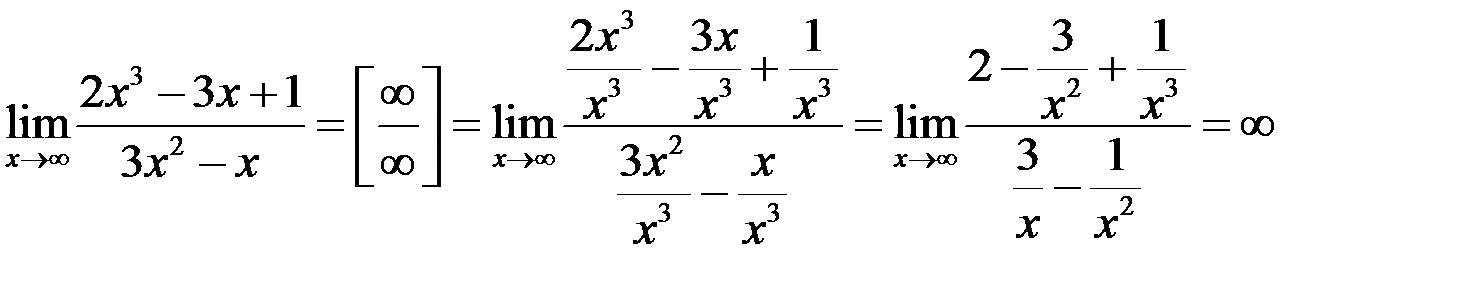 .
.
Замечание. Из рассмотренных примеров видно, что предел частного двух многочленов при 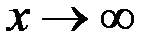 равен отношению коэффициентов при старших членах, если степени многочленов, стоящих в числителе и знаменателе, равны; равен нулю, если степень числителя меньше степени знаменателя; равен ¥, если степень числителя больше степени знаменателя.
равен отношению коэффициентов при старших членах, если степени многочленов, стоящих в числителе и знаменателе, равны; равен нулю, если степень числителя меньше степени знаменателя; равен ¥, если степень числителя больше степени знаменателя.
3.2. Раскрытие неопределенности вида 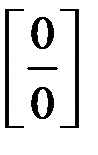
Рассмотрим отношение функций 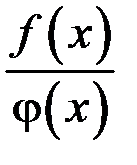 . Пусть
. Пусть 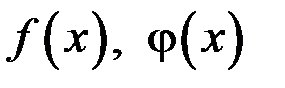 – бесконечно малые функции (б.м.ф.) при
– бесконечно малые функции (б.м.ф.) при 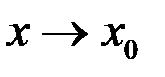 , отношение
, отношение 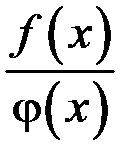 в этом случае называется неопределенным выражением вида
в этом случае называется неопределенным выражением вида 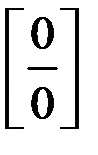 .
.
Чтобы раскрыть неопределенность вида 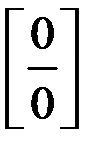 , заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель и сократить на него.
, заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель и сократить на него.
Чтобы раскрыть неопределенность вида 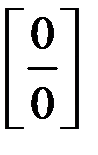 , в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности, домножив числитель и знаменатель на сопряженное выражение.
, в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности, домножив числитель и знаменатель на сопряженное выражение.
Пример
Вычислить предел 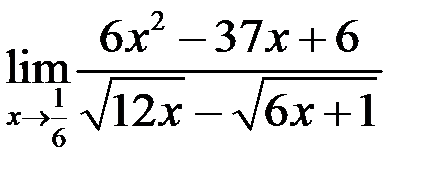 .
.
Решение
При 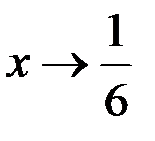 числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида
числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида  . Для раскрытия неопределенности числитель и знаменатель дроби умножим на сопряженное знаменателю выражение, т.е. на сумму
. Для раскрытия неопределенности числитель и знаменатель дроби умножим на сопряженное знаменателю выражение, т.е. на сумму 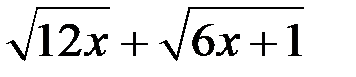 , а квадратный трехчлен
, а квадратный трехчлен 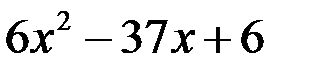 разложим на множители, найдя для этого его корни:
разложим на множители, найдя для этого его корни:
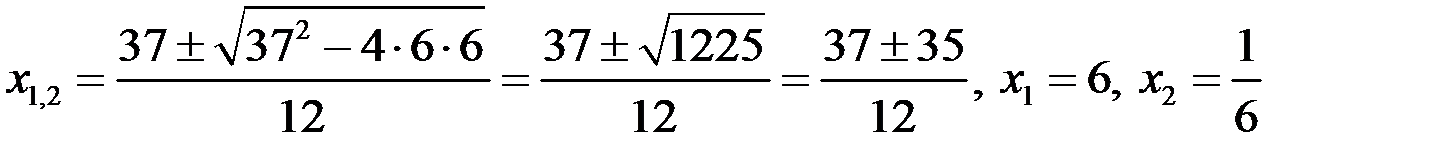 ,
,
тогда,
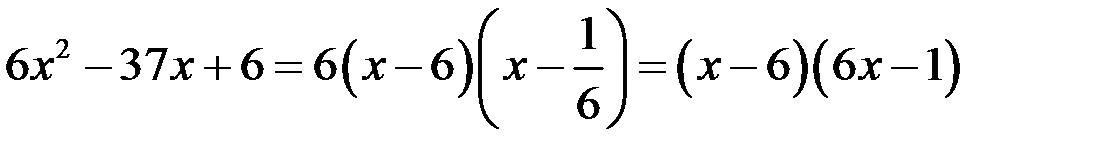 .
.
Таким образом, получим:
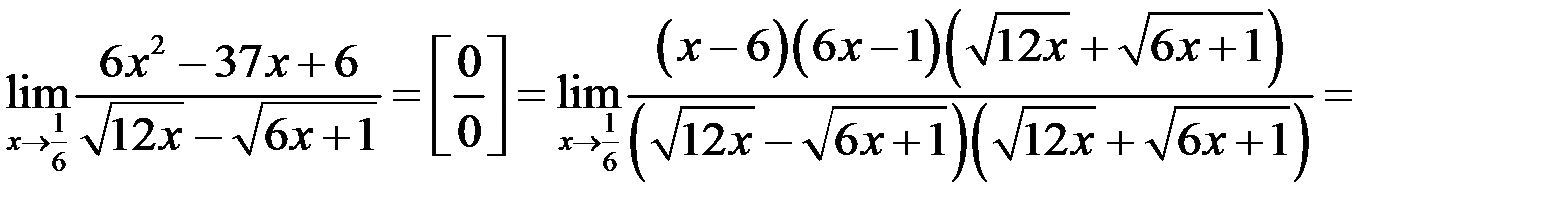
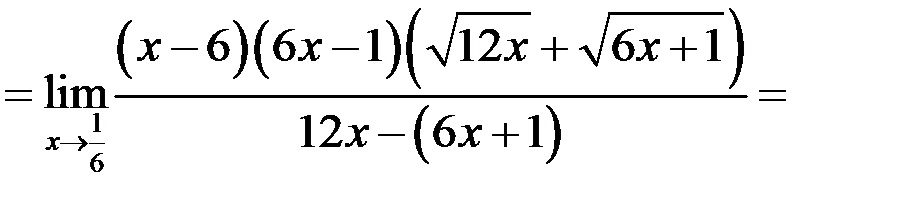
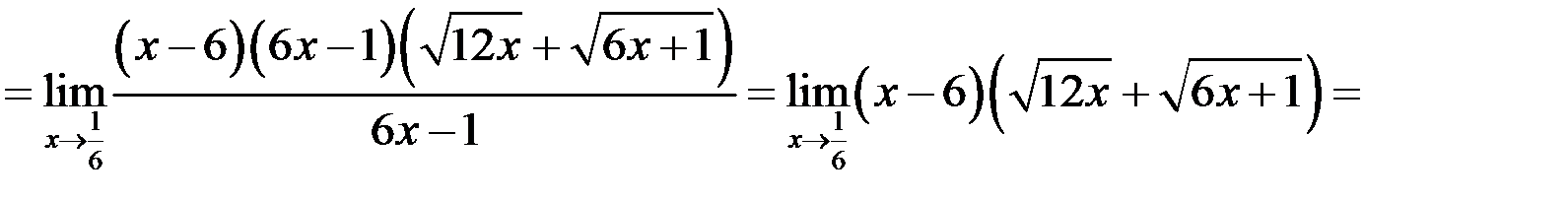
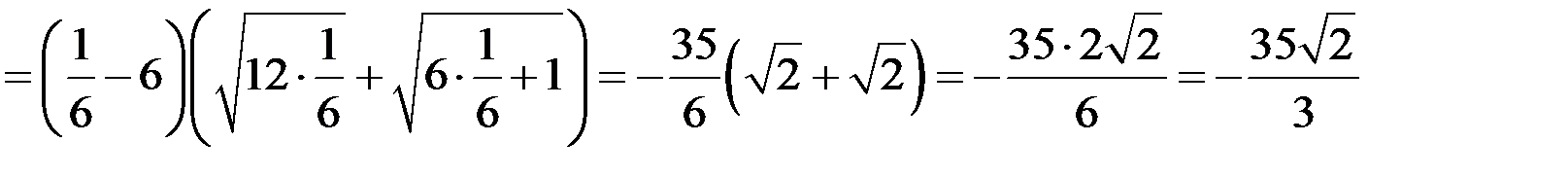 .
.
Пример
Вычислить предел 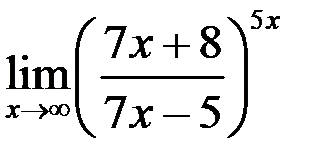 .
.
Решение
Предел основания 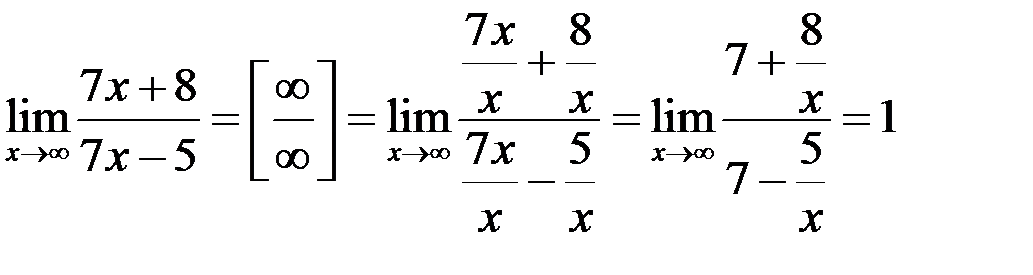 , а показатель степени
, а показатель степени 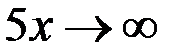 при
при 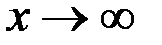 , т.е. имеет место неопределенность вида
, т.е. имеет место неопределенность вида 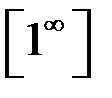 . Выделим целую часть основания степени
. Выделим целую часть основания степени
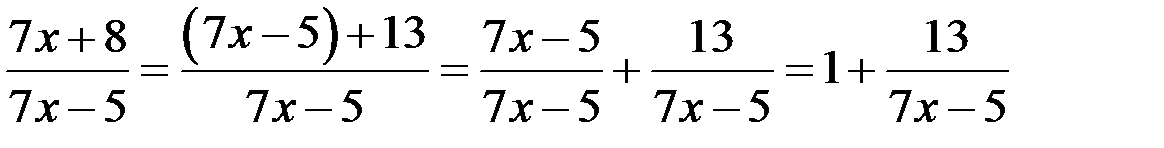
и применим второй замечательный предел:
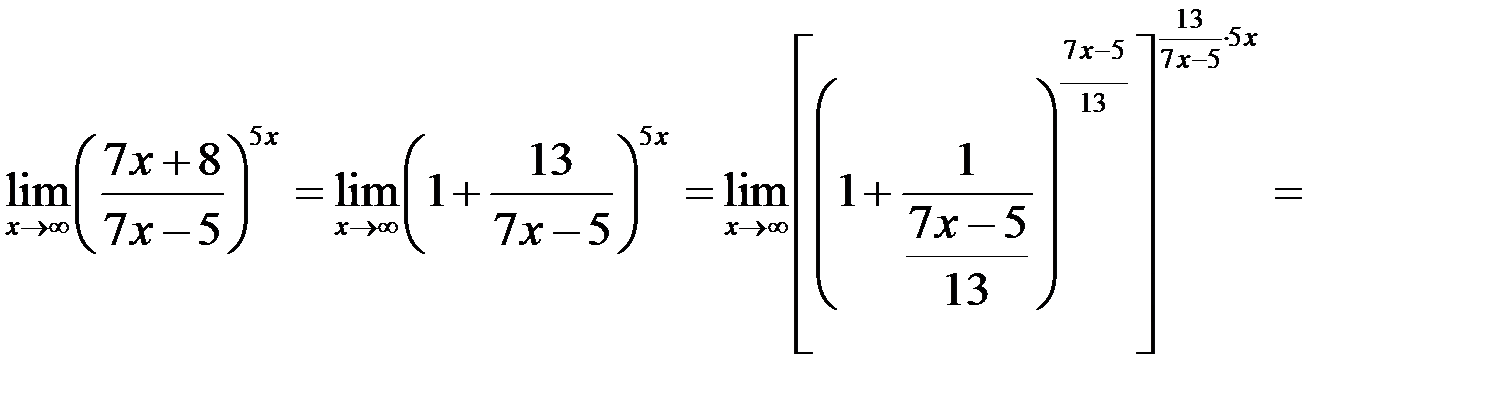
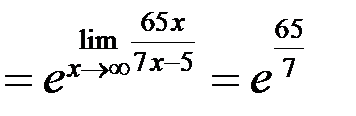 , учитывая, что
, учитывая, что 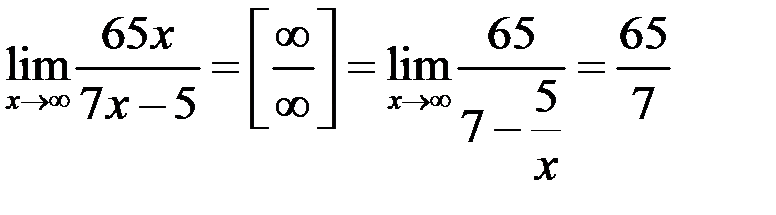 .
.
Непрерывность функции
Пусть функция 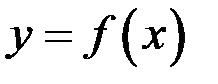 определена в некоторой окрестности точки
определена в некоторой окрестности точки 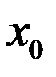 .
.
Определение. Функция 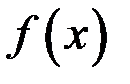 называется непрерывной в точке
называется непрерывной в точке 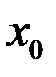 , если она имеет предел в точке
, если она имеет предел в точке 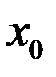 и этот предел равен
и этот предел равен 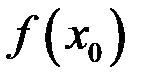 – значению функции
– значению функции 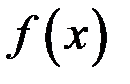 в точке
в точке 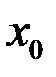 :
:
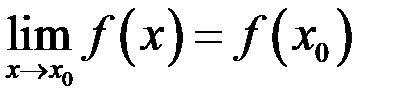 .
.
Таким образом, для того чтобы функция 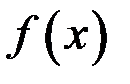 была непрерывна в точке
была непрерывна в точке 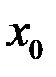 , необходимо и достаточно выполнение трех условий:
, необходимо и достаточно выполнение трех условий:
1) функция 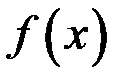 должна быть определена в точке
должна быть определена в точке 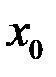 ;
;
2) должны существовать пределы функции 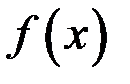 при
при 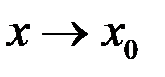 как слева, так и справа, т.е.
как слева, так и справа, т.е. 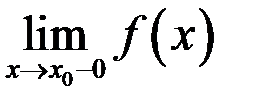 и
и 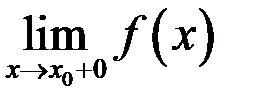 ;
;
3) эти пределы должны быть равны между собой и равны значению функции 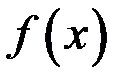 в точке
в точке 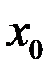 , т.е.
, т.е. 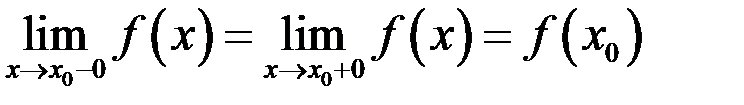 .
.
Если хотя бы одно из этих условий не выполнено, то говорят, что функция имеет разрыв в точке 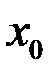 и точку
и точку 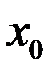 называют точкой разрыва функции
называют точкой разрыва функции 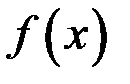 .
.
Точки разрыва следует искать среди точек, не входящих в область определения функции.
Классификация точек разрыва
Определение. Если в точке 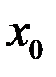 функция
функция 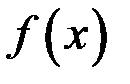 имеет пределы слева и справа и они равны между собой, а в точке
имеет пределы слева и справа и они равны между собой, а в точке 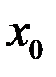
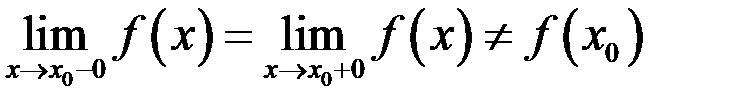
или функция не определена, то точка 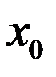 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 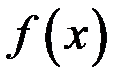 .
.
В этом случае функцию можно доопределить в точке 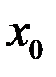 так, чтобы она стала непрерывной, т.е. положить
так, чтобы она стала непрерывной, т.е. положить
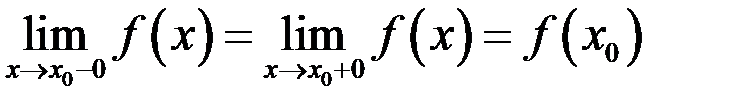 .
.
Определение. Если в точке 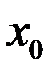 функция
функция 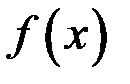 имеет конечные пределы слева и справа, причем
имеет конечные пределы слева и справа, причем 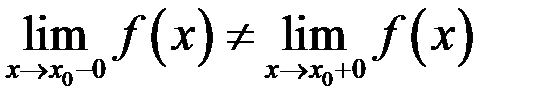 , то точка
, то точка 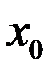 называется точкой разрыва функции
называется точкой разрыва функции 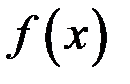 1-го рода.
1-го рода.
При переходе через точку 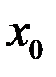 значение функции
значение функции 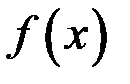 претерпевает скачок, измеряемый разностью
претерпевает скачок, измеряемый разностью 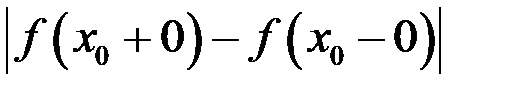 .
.
Определение. Точка 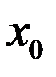 называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен
называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен 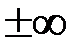 .
.
Пример
В точках 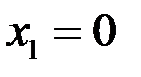 и
и 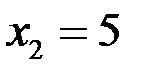 для функции
для функции 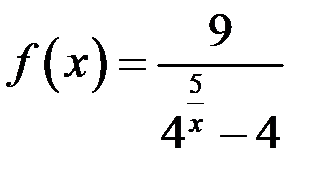 установить характер точек разрыва.
установить характер точек разрыва.
Решение
Область определения функции 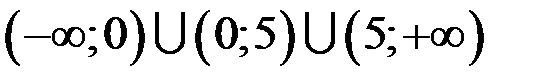 . Данная функция непрерывна во всех точках, кроме точек
. Данная функция непрерывна во всех точках, кроме точек 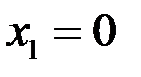 и
и 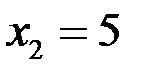 , которые не входят в область определения функции.
, которые не входят в область определения функции.
Исследуем точку 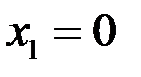 , находя ее односторонние пределы в этой точке:
, находя ее односторонние пределы в этой точке:
если 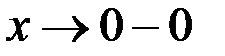 , то
, то 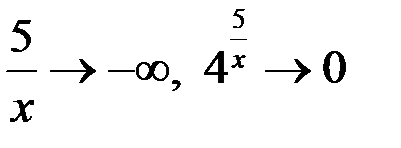 , тогда предел слева
, тогда предел слева 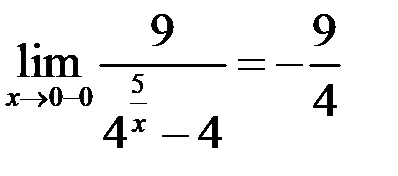 ,
,
если 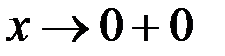 , то
, то 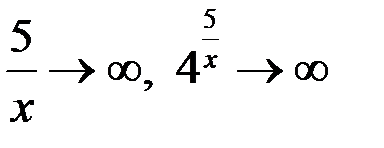 , тогда предел справа
, тогда предел справа 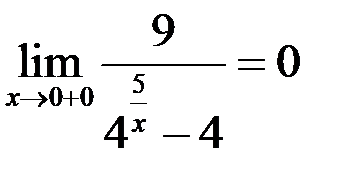 .
.
Так как односторонние пределы конечны, но не равны между собой, то в точке 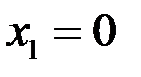 функция
функция 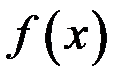 имеет разрыв 1-го рода (скачок функции).
имеет разрыв 1-го рода (скачок функции).
Исследуем точку 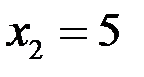 , находя ее односторонние пределы в этой точке:
, находя ее односторонние пределы в этой точке:
если 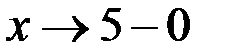 , то
, то 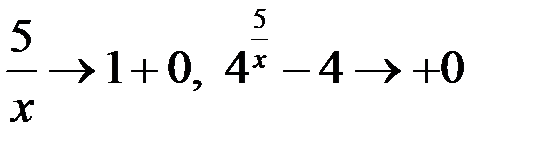 , тогда
, тогда 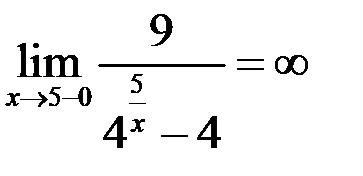 ,
,
если 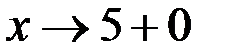 , то
, то 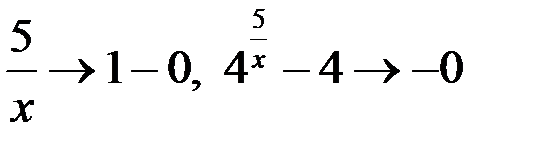 , тогда
, тогда 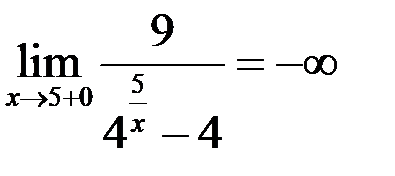 .
.
Так как односторонние пределы равны 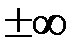 , то в точке
, то в точке 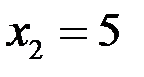 функция
функция 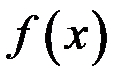 имеет разрыв 2-го рода.
имеет разрыв 2-го рода.
Правила дифференцирования
Определение. Производной функции 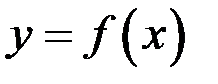 в данной точке х называется предел отношения приращения функции к приращению аргумента, при
в данной точке х называется предел отношения приращения функции к приращению аргумента, при 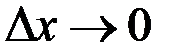 , если он существует.
, если он существует.
По определению
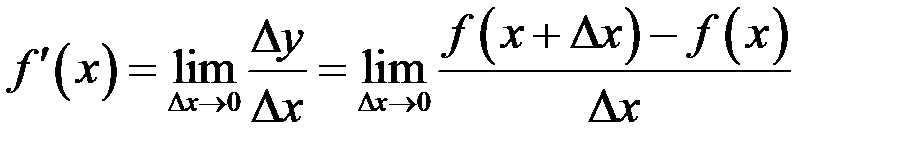 .
.
Таблица производных
| № | № | ||
| 1 | 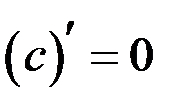 , , 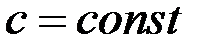
| 10 | 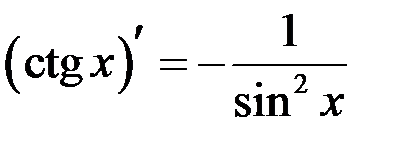
|
| 2 | 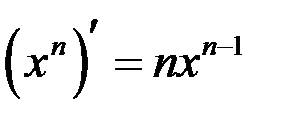
| 11 | 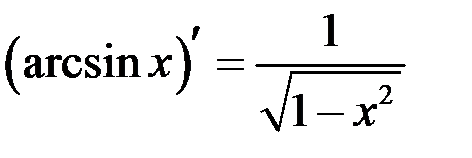
|
| 3 | 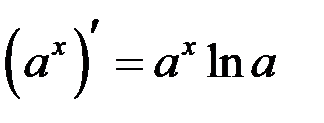
| 12 | 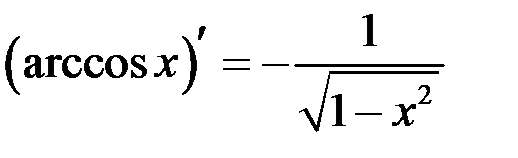
|
| 4 | 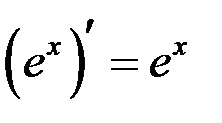
| 13 | 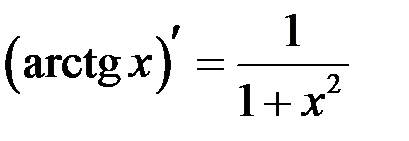
|
| 5 | 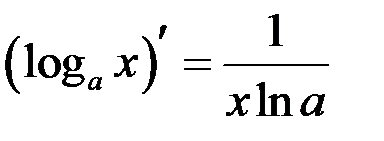
| 14 | 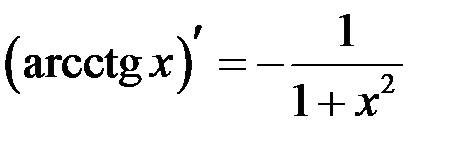
|
| 6 | 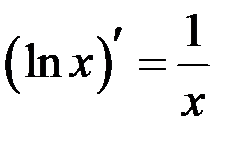
| 15 | 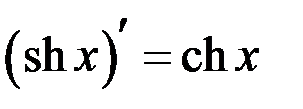
|
| 7 | 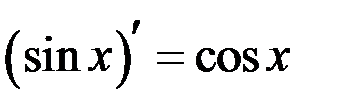
| 16 | 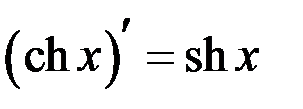
|
| 8 | 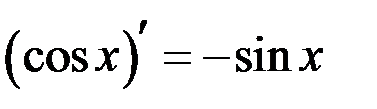
| 17 | 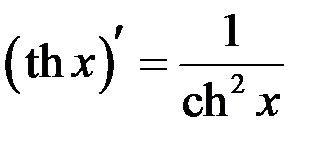
|
| 9 | 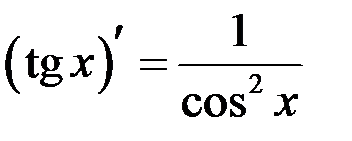
| 18 | 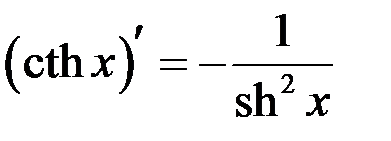
|
Правила дифференцирования
1. Производная постоянной равна нулю: 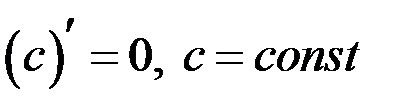 .
.
2.
Теорема. Если каждая из функций 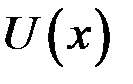 и
и 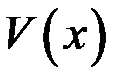 дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии
дифференцируема в данной точке х, то сумма, разность, произведение и частное (частное при условии 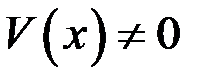 ) так же дифференцируемы в этой точке, причем имеют место формулы:
) так же дифференцируемы в этой точке, причем имеют место формулы:
1) 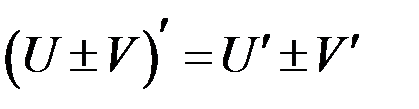 ,
,
2) 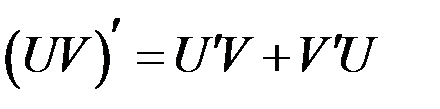 ,
,
3) 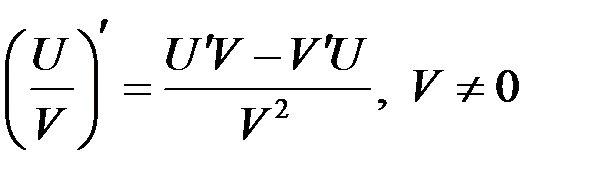 .
.
Следствие. Постоянный множитель можно выносить за знак производной:
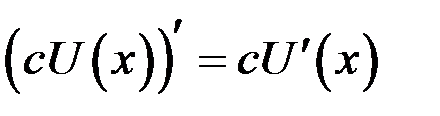 .
.
Пример
Используя таблицу производных и правила дифференцирования, найти производную функции 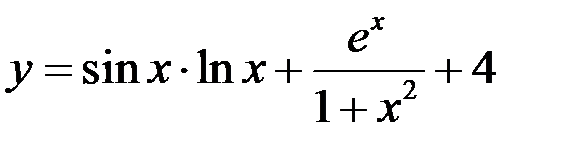 .
.
Решение
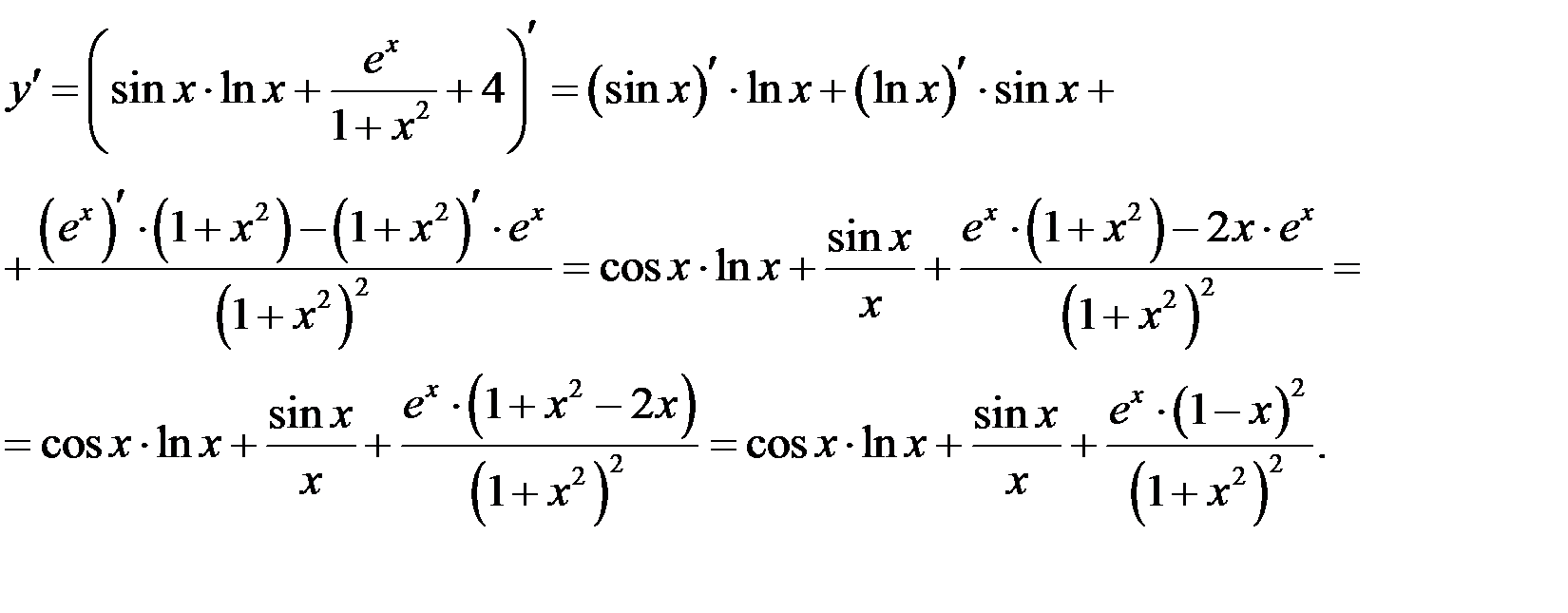
Производная сложной функции
Пусть дана сложная функция 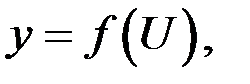 где
где 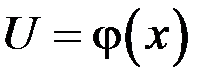 или
или 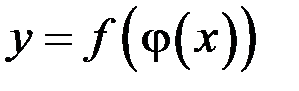 .
.
Теорема. Если функция 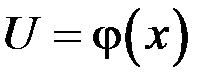 дифференцируема в точке
дифференцируема в точке 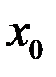 , а функция
, а функция 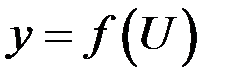 дифференцируема в точке
дифференцируема в точке 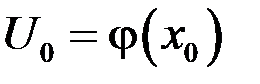 , тогда сложная функция
, тогда сложная функция 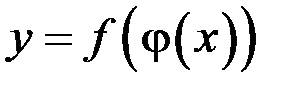 дифференцируема в точке
дифференцируема в точке 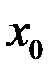 , причем
, причем
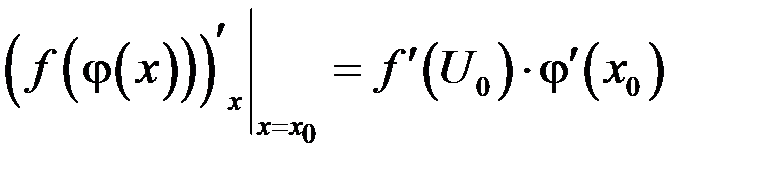 или
или 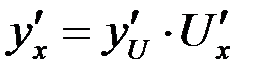
Замечание. Теорема может быть обобщена на случай любой конечной цепочки функций. Так, если 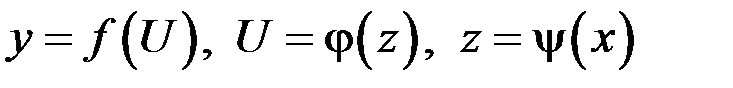 , или
, или 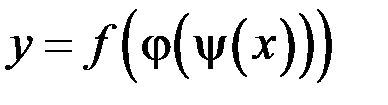 и существуют производные
и существуют производные 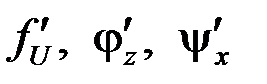 , то
, то 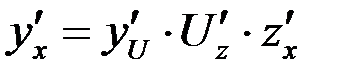 .
.
Пример
Найти производную функции 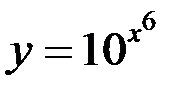 .
.
Решение
Здесь 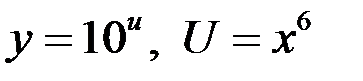 ,
,
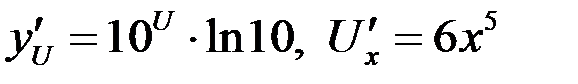 , тогда
, тогда 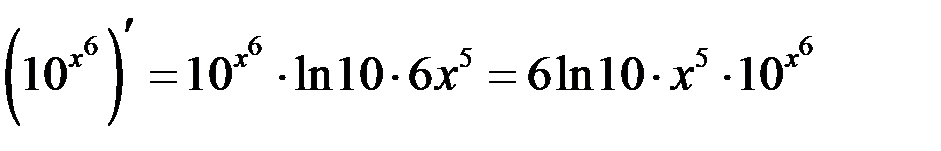 .
.
Пример
Найти производную функции 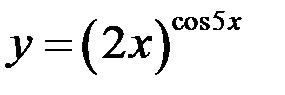 применяя метод логарифмического дифференцирования.
применяя метод логарифмического дифференцирования.
Решение
Здесь основание и показатель степени зависит от х. Логарифмируем обе части равенства 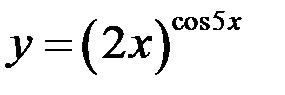 по основанию е:
по основанию е:
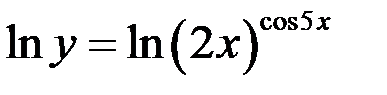 ,
,
применяя свойства логарифмов, получим
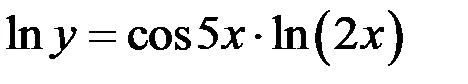 .
.
Продифференцируем обе части последнего равенства по х, рассматривая у как функцию х:
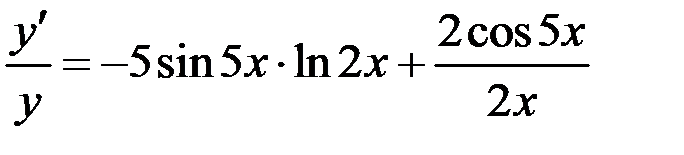 ,
,
умножим обе части равенства на у и подставим вместо у его выражение 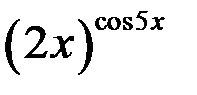 , получим
, получим
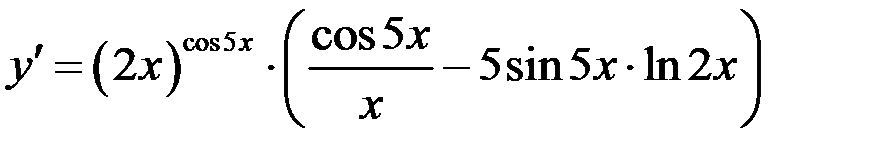 .
.
Пример
Найти производную функции, заданной неявно: 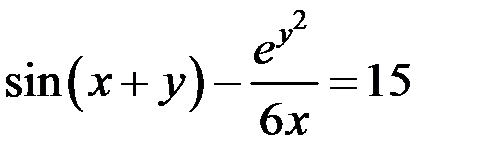 .
.
Решение
Продифференцируем обе части данного уравнения по аргументу х:
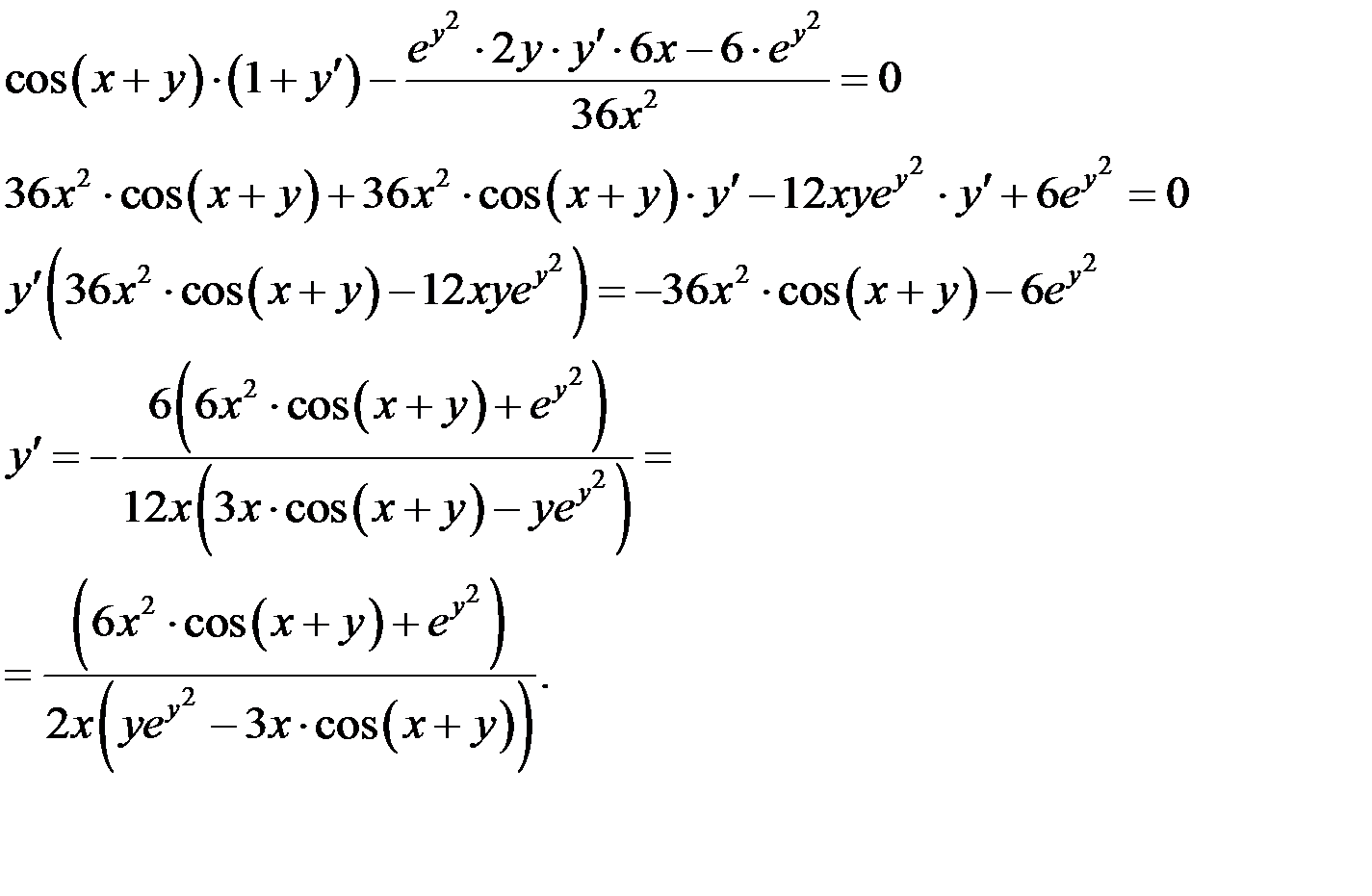
Пример
С помощью методов дифференциального исчисления исследовать и построить график функции 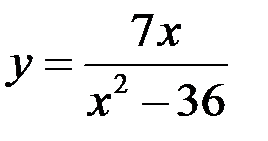 .
.
Решение
1. Область определения функции находится из условия: 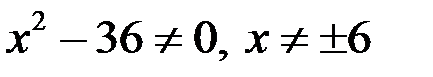 , т.е.
, т.е. 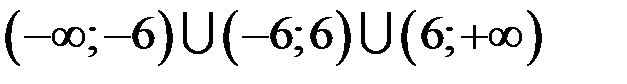 .
.
2. Точки пересечения графика функции с осями координат:
с осью Оу, 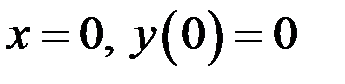 , точка
, точка 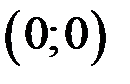 ,
,
с осью Ох, 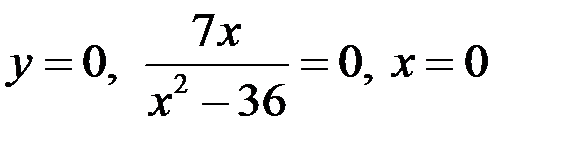 , точка
, точка 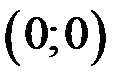 .
.
3. Четность, нечетность.
Функция 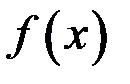 называется четной, если для любого х из области определения справедливо равенство
называется четной, если для любого х из области определения справедливо равенство 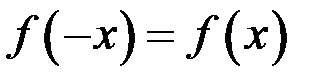 . Функция
. Функция 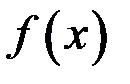 называется нечетной, если для любого х из области определения справедливо равенство
называется нечетной, если для любого х из области определения справедливо равенство 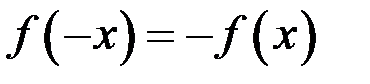 . Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
. Если не выполнено ни одно из равенств, то функцию называют функцией общего вида.
В нашем случае, 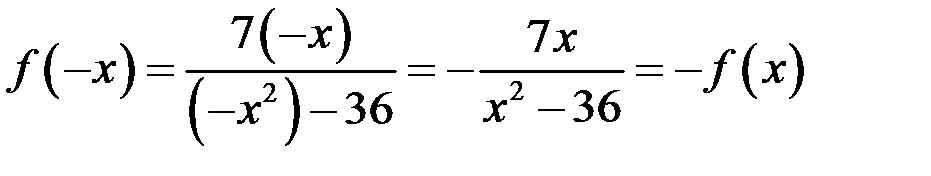 , следовательно, функция нечетная, а ее график симметричен относительно начала координат.
, следовательно, функция нечетная, а ее график симметричен относительно начала координат.
4. Точки разрыва функции и асимптоты графика функции.
1) Вертикальные асимптоты. Прямая 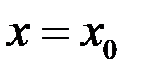 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 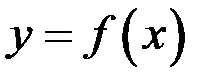 , если хотя бы один из пределов
, если хотя бы один из пределов
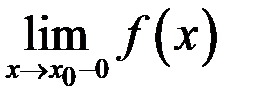 или
или 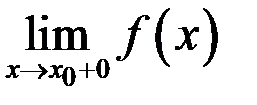
равен 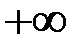 или
или 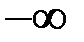 . Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
. Таким образом, для нахождения вертикальных асимптот следует найти все точки разрыва 2-го рода данной функции. Если точек разрыва нет, то нет и вертикальных асимптот.
Заданная функция имеет две точки разрыва второго рода 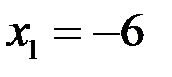 и
и 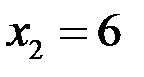 , так как
, так как
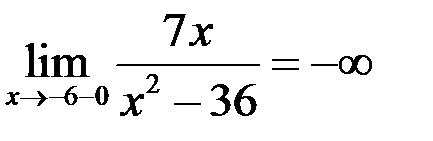 ,
, 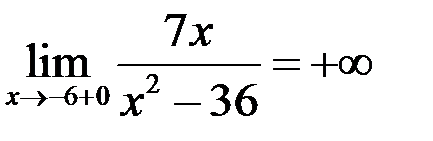 ,
,
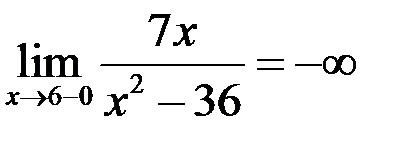 ,
, 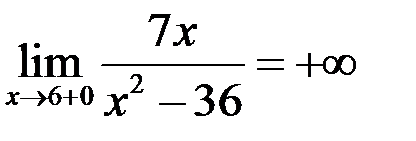 ,
,
следовательно, график функции имеет две вертикальных асимптоты 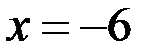 и
и 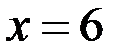 .
.
2) Горизонтальные асимптоты. Горизонтальная асимптота – частный случай наклонной асимптоты, когда 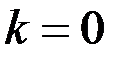 .
.
Чтобы найти горизонтальные асимптоты графика функции, нужно найти пределы:
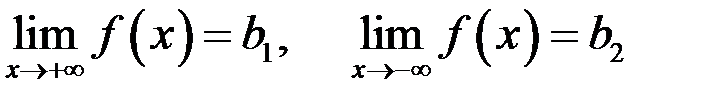 .
.
Если эти пределы конечны и различны, то прямые 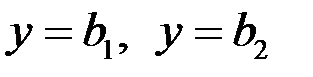 будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен
будут горизонтальными асимптотами. Если какой-либо из этих пределов не существует или равен 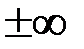 , то не существуют и соответствующие асимптоты.
, то не существуют и соответствующие асимптоты.
Так как
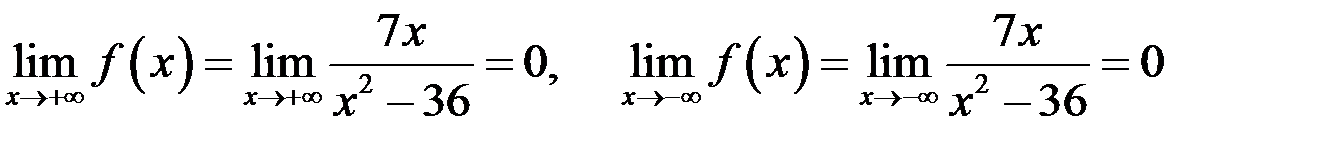 ,
,
то график функции имеет горизонтальную асимптоту 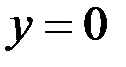 .
.
3) Наклонные асимптоты. Пусть прямая 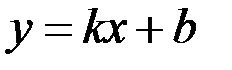 является асимптотой графика функции
является асимптотой графика функции 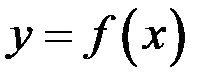 . Такую асимптоту называют наклонной. Для того, чтобы график функции
. Такую асимптоту называют наклонной. Для того, чтобы график функции 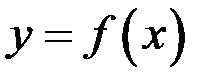 имел при
имел при 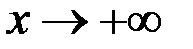 наклонную асимптоту
наклонную асимптоту 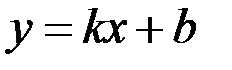 , необходимо и достаточно, чтобы существовали оба предела:
, необходимо и достаточно, чтобы существовали оба предела:
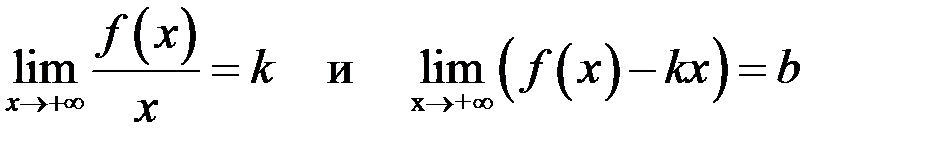 .
.
Аналогично находится асимптота при 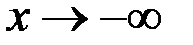 .
.
Так как 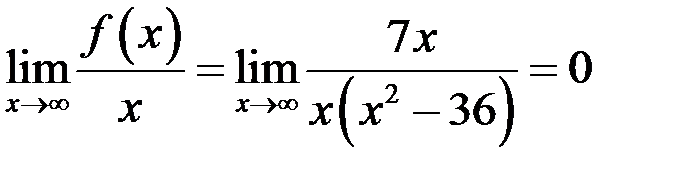 , то наклонных асимптот нет.
, то наклонных асимптот нет.
5. Исследование функции на экстремум.
Для определения интервалов возрастания и убывания функции и ее точек экстремума найдем первую производную:
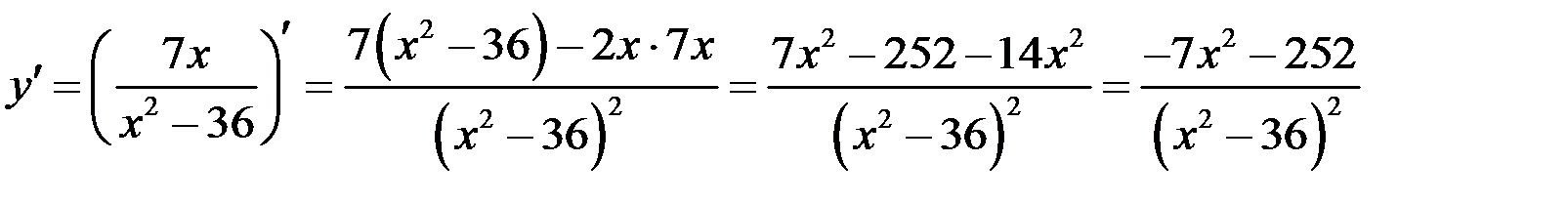 .
.
Найдем критические точки, т.е. точки, в которых производная равна нулю или не существует, для чего приравниваем числитель 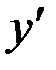 к нулю:
к нулю:
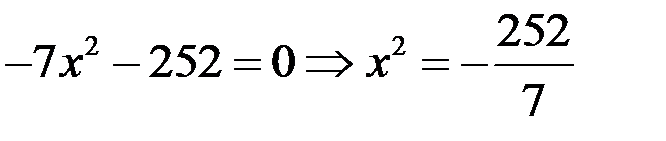 , т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
, т.е. вещественных корней нет, следовательно, точек экстремума нет. Так как производная отрицательна во всей области определения функции, то она всюду убывает в этой области.
_ _ _ 
х
-6 6 у
6. Исследование на выпуклость, вогнутость. Точки перегиба.
Вычислим производную второго порядка:
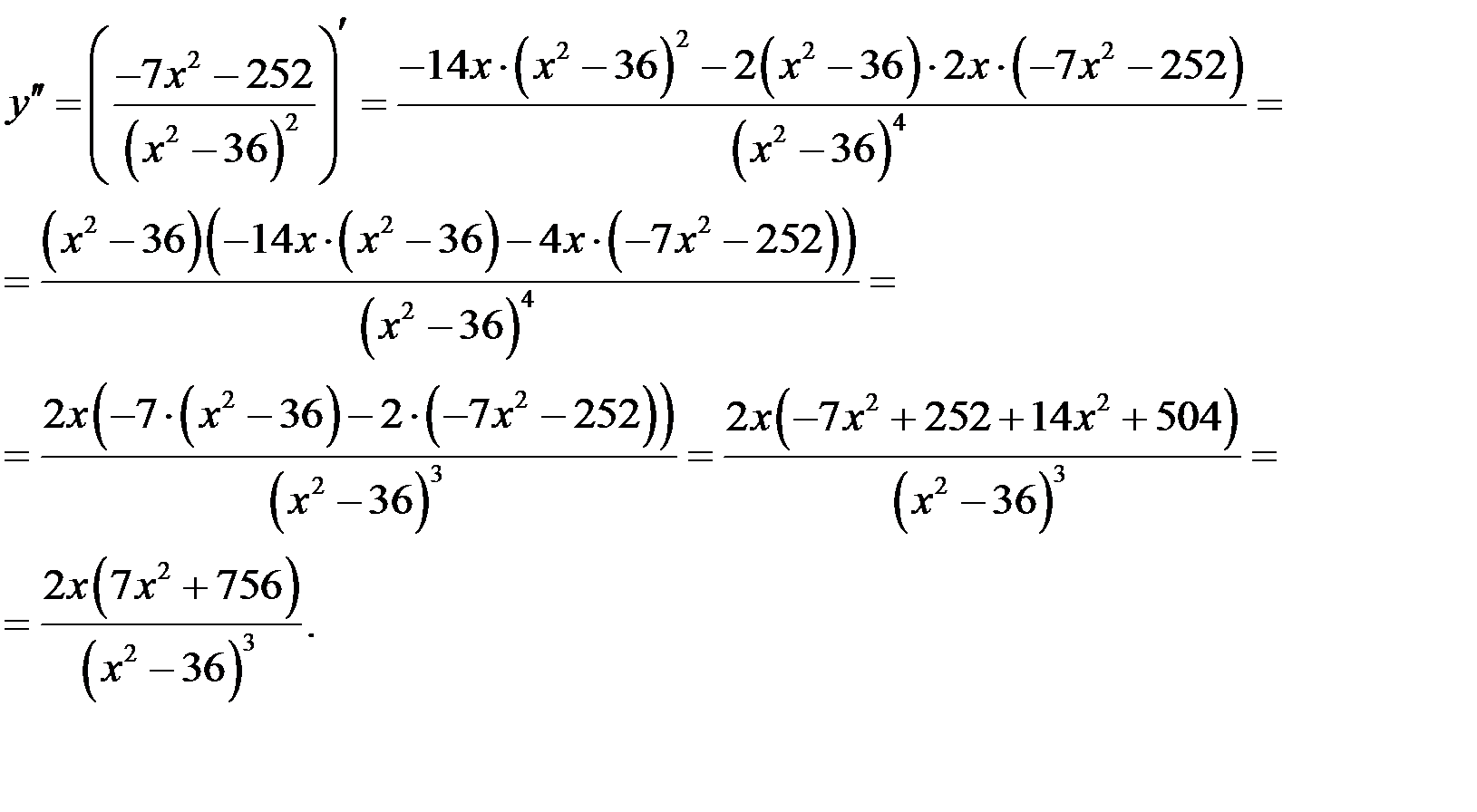 Необходимое условие точки перегиба:
Необходимое условие точки перегиба: 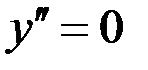 или не существует. Равенство
или не существует. Равенство 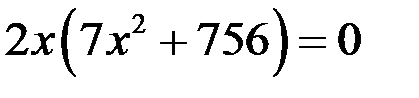 выполняется при
выполняется при 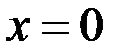 , следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
, следовательно, эта точка является «подозрительной» на точку перегиба. Определим знак второй производной на всей числовой оси и укажем на ней интервалы выпуклости и вогнутости функции.
_ + _ + 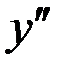
х
 -6
-6  0
0  6
6  у
у
Так как при переходе через точку 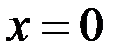 вторая производная меняет знак, то точка с абсциссой
вторая производная меняет знак, то точка с абсциссой 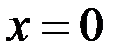 является точкой перегиба. Итак, точка перегиба имеет координаты
является точкой перегиба. Итак, точка перегиба имеет координаты 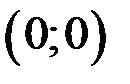 .
.
7. Построение графика функции.

Таблица интегралов
1. 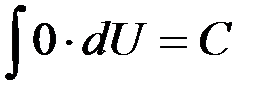
| 8. 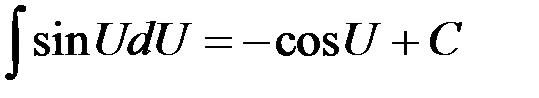
|
2. 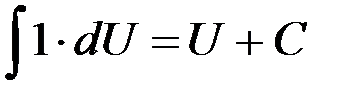
| 9. 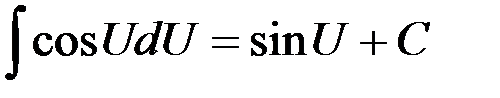
|
3. 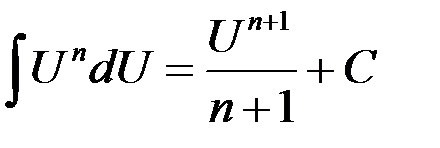
| 10. 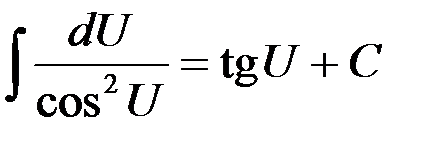
|
4. 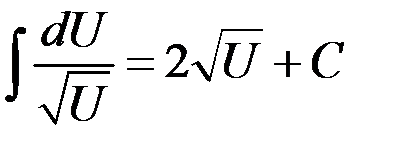
| 11. 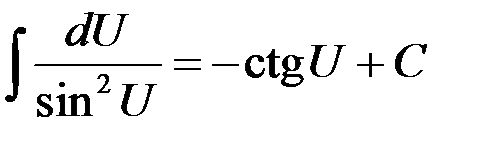
|
5. 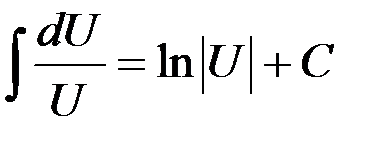
| 12. 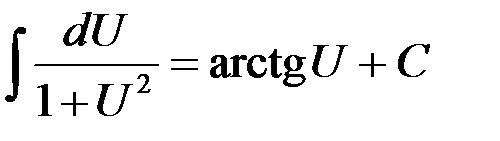
|
6. 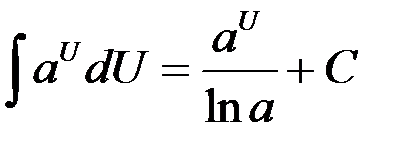
| 13. 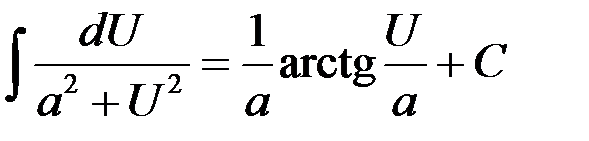
|
7. 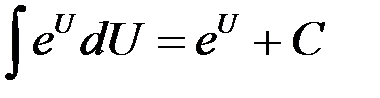
| 14. 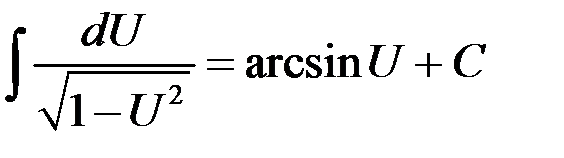
|
| 15. | |
При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:
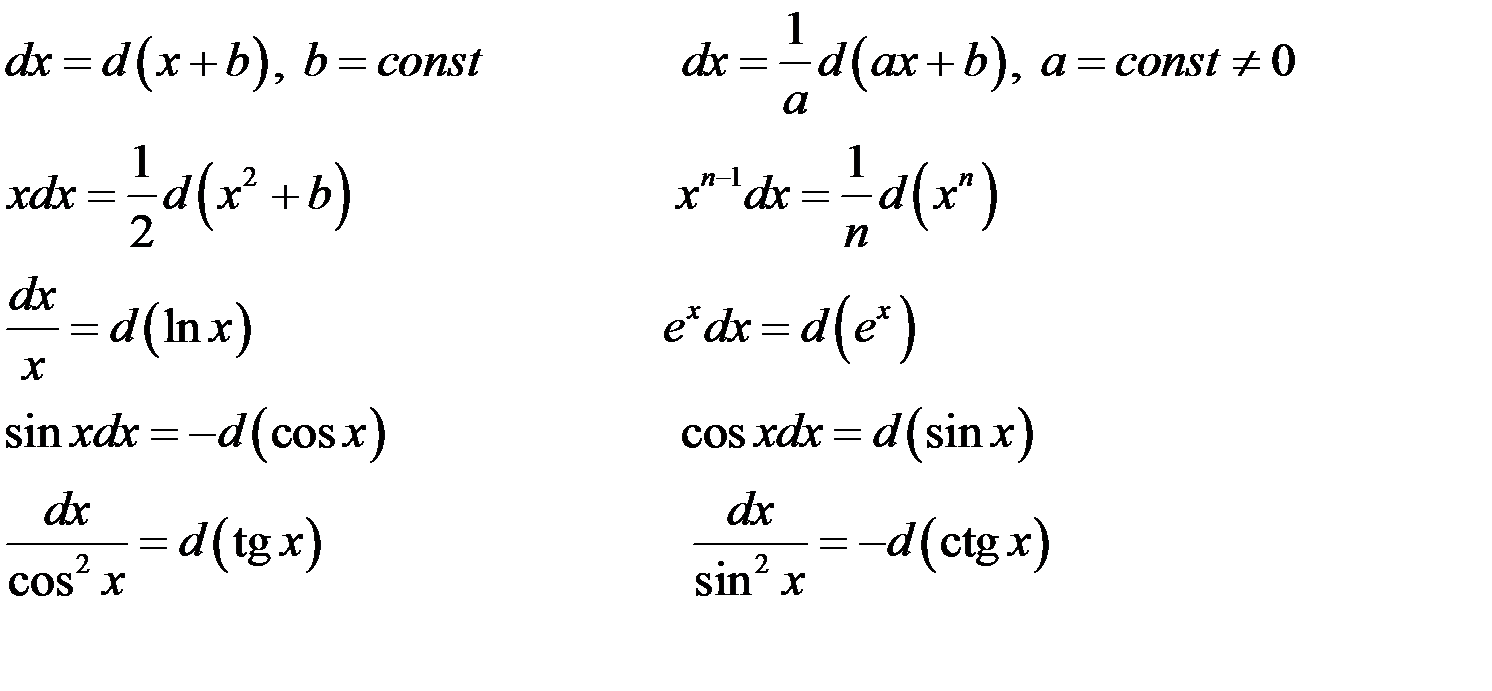
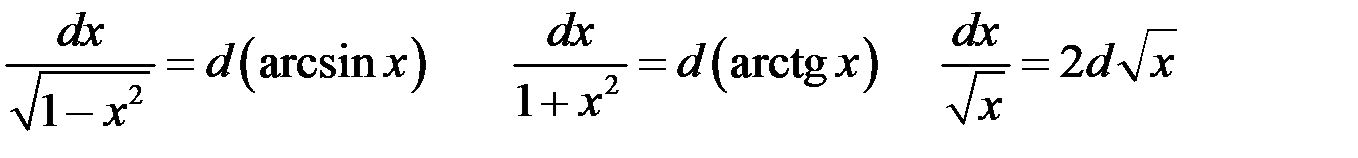
В общем случае
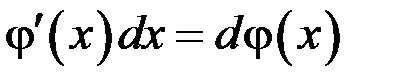 .
.
Пример 1
Найти интеграл 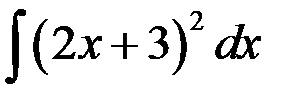 .
.
Так как 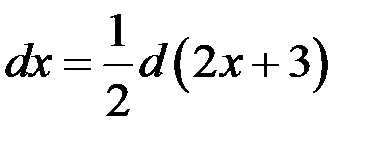 , то
, то
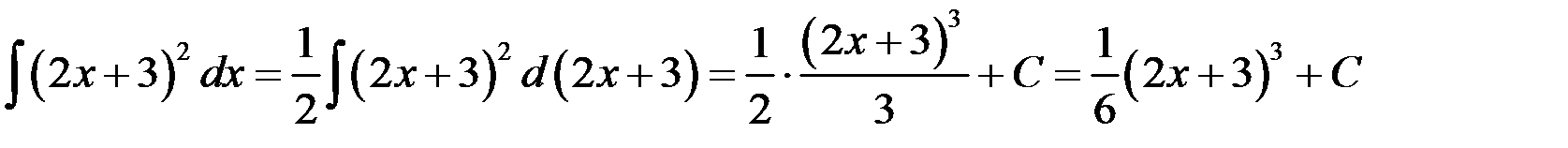 .
.
Пример 2
Найти интеграл 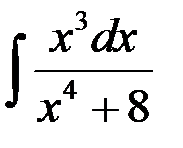 .
.
Так как 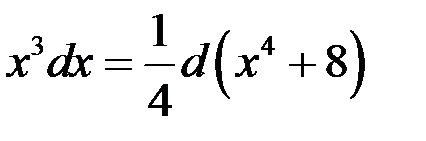 , то
, то
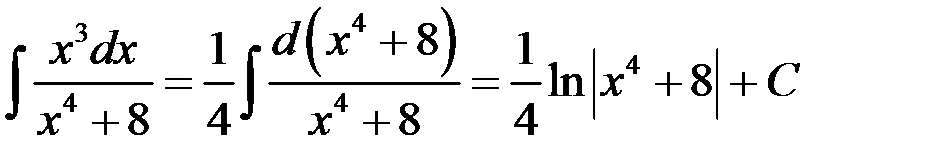 .
.
Пример 3
Найти интеграл 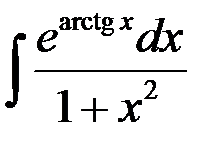 .
.
Так как 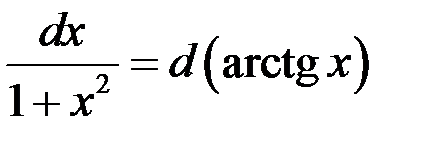 , то
, то
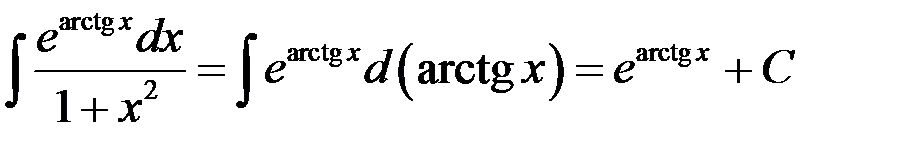
Пример 4
Найти интеграл 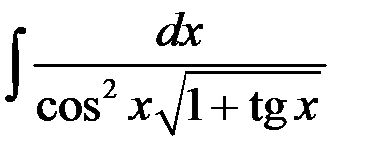 .
.
Так как 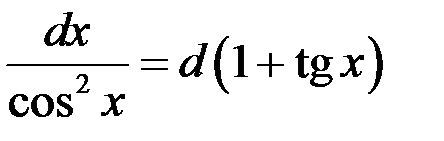 , то
, то
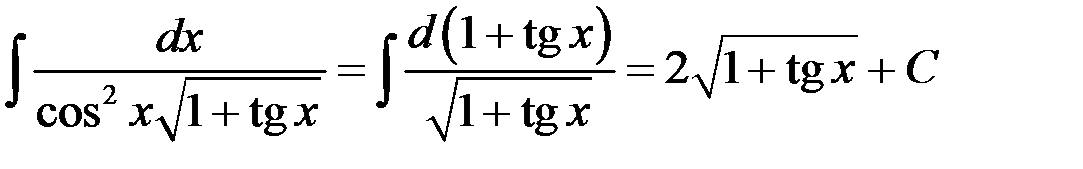 .
.
Пример
Найти интеграл  .
.
Решение
Положим 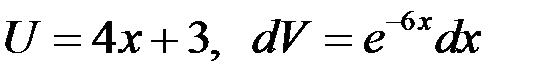 , найдем
, найдем 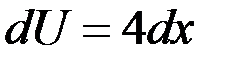 ,
, 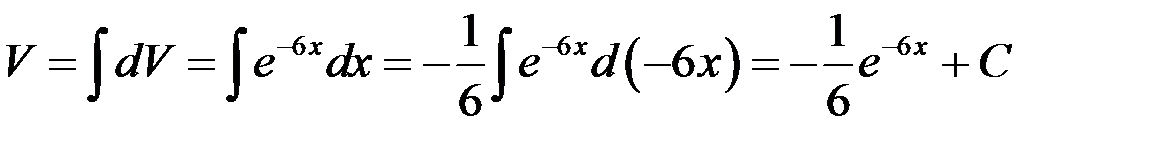 . Так как достаточно взять одну из первообразных, то принимаем
. Так как достаточно взять одну из первообразных, то принимаем 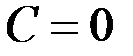 . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям
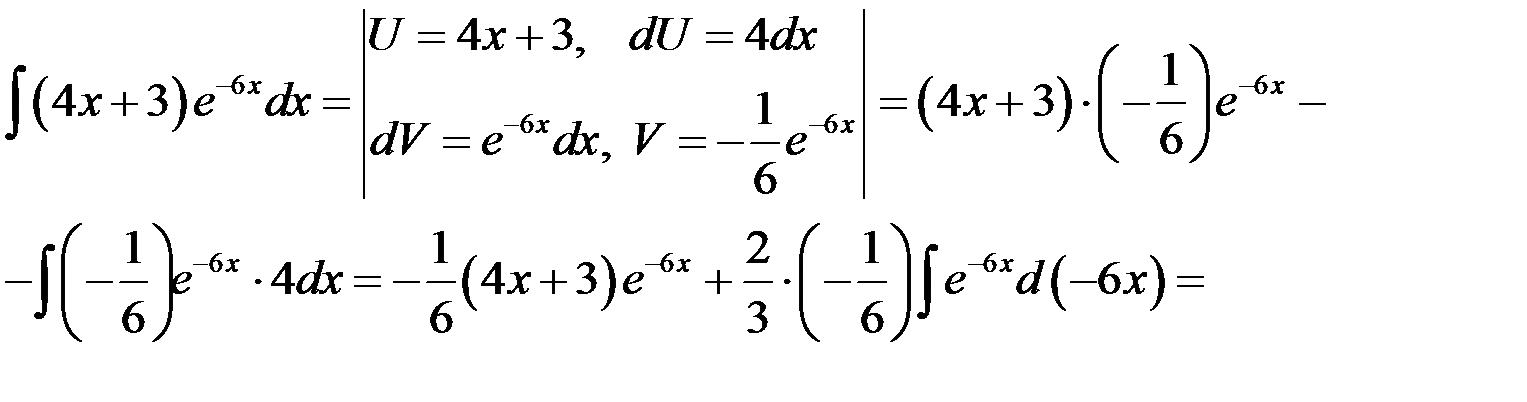
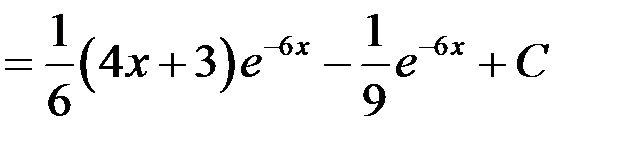 .
.
Пример
Найти интеграл 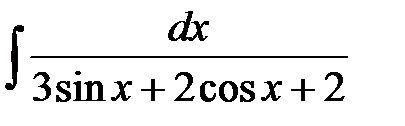 .
.
Решение
Применим универсальную подстановку
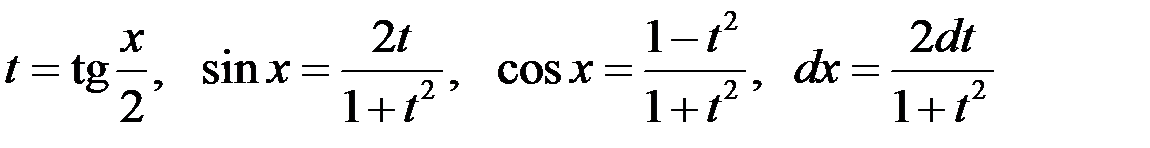 ,
,
получим
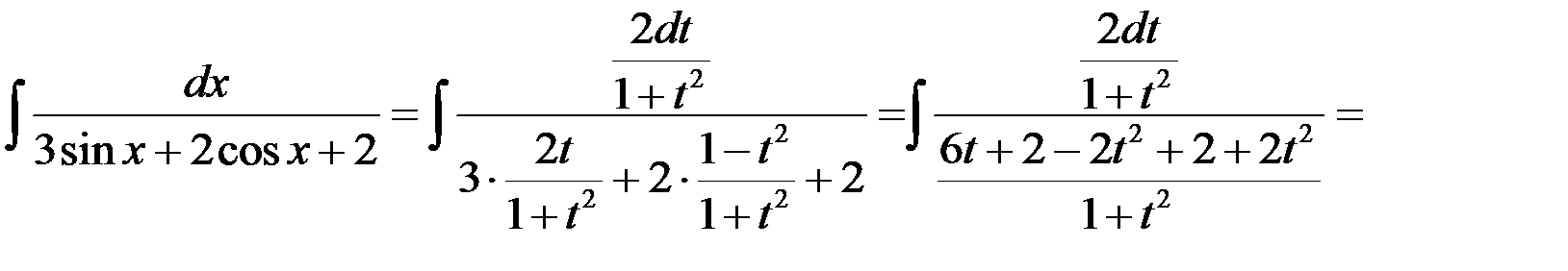
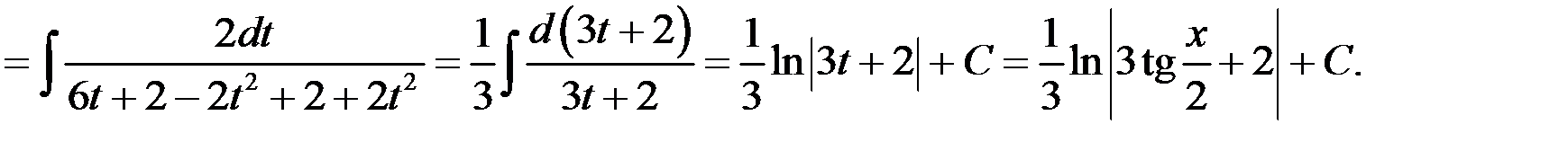
Пример 1
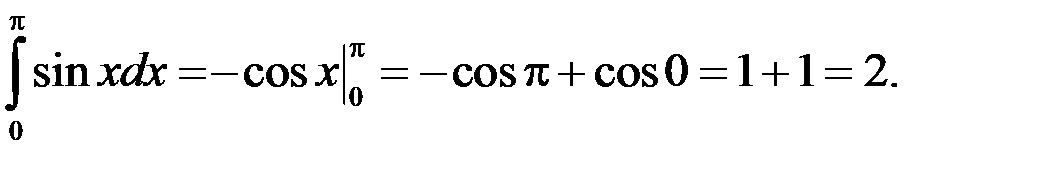
Если 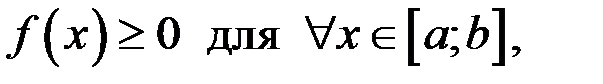 то
то 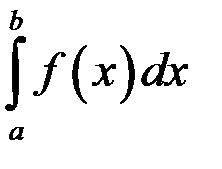 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 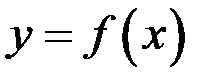 ,
,
прямыми 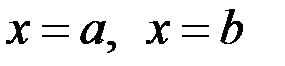 и осью ох:
и осью ох:
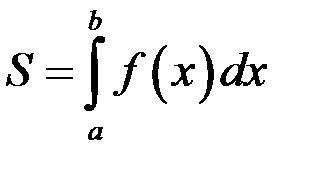
Если 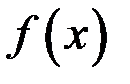 меняет знак конечное число раз на отрезке
меняет знак конечное число раз на отрезке 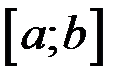 , то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где
, то интеграл по всему отрезку разбивается на сумму интегралов по частичным отрезкам, интеграл будет положителен там, где 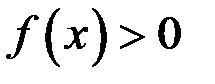 и отрицателен, где
и отрицателен, где 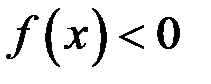 :
:
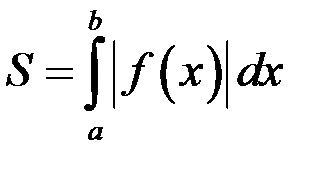 .
.
Пусть нужно вычислить площадь фигуры, ограниченной кривыми 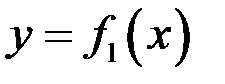 и
и 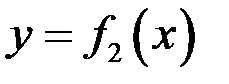 и прямыми
и прямыми 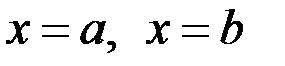 , тогда при условии
, тогда при условии 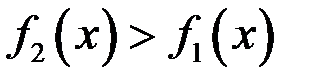 имеем
имеем
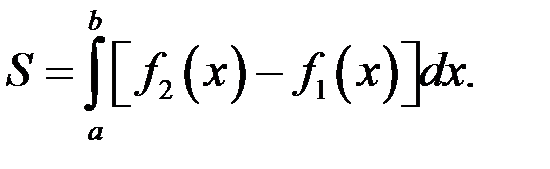
Пример 2
Вычислить площадь фигуры, ограниченной линиями 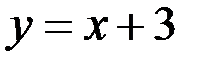 и
и 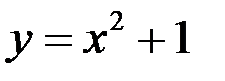 .
.
Решение
| у у=х+3 у=х2+1 3 –3 –1 0 2 х | Найдем точки пересечения: 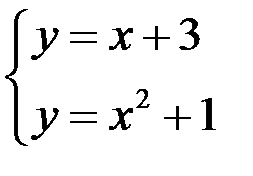 , , 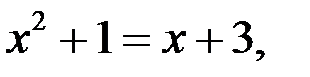
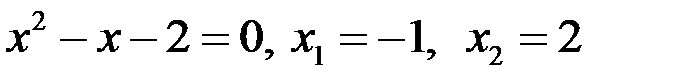 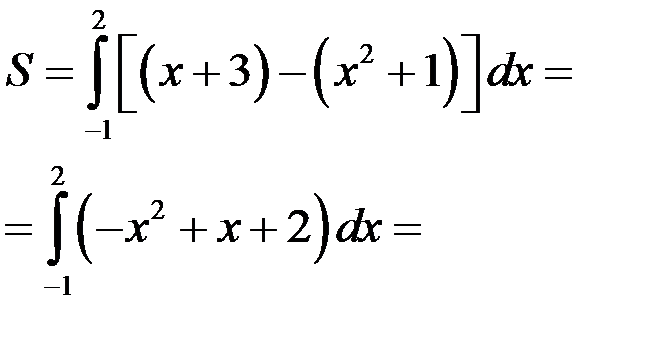
|
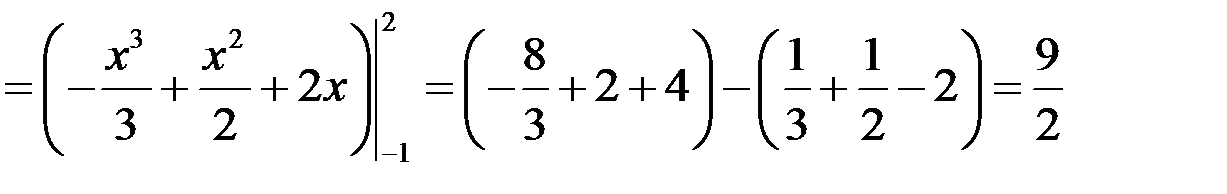 .
.
Аналогично,
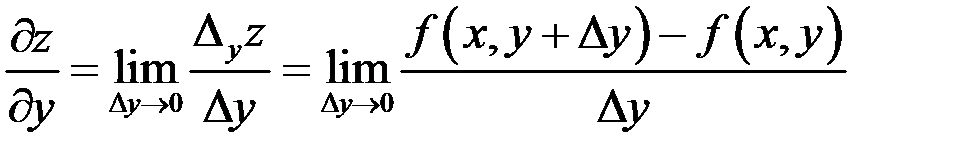 .
.
Так как 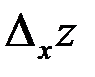 вычисляется при неизменном значении переменной у, а
вычисляется при неизменном значении переменной у, а 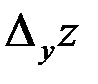 – при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции
– при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции 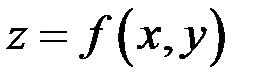 называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции
называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции 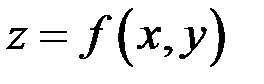 называется ее производная по у, вычисленная в предположении, что х – постоянная.
называется ее производная по у, вычисленная в предположении, что х – постоянная.
Пример 1
Найти частные производные функции 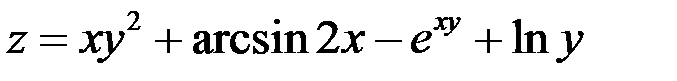 .
.
Решение
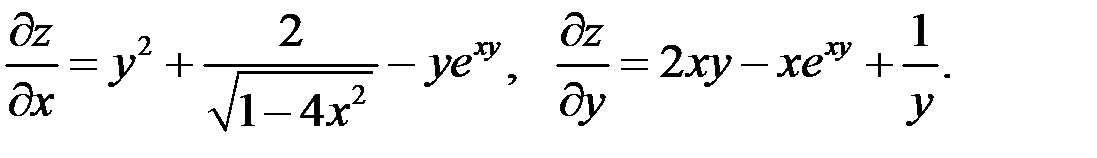
Пример 2
Показать, что функция 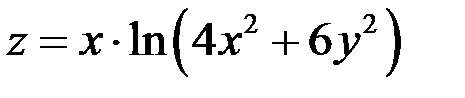 удовлетворяет уравнению
удовлетворяет уравнению 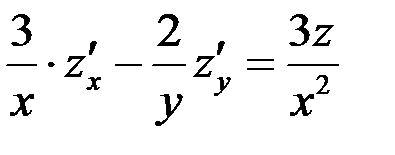 .
.
Решение
Найдем частные производные
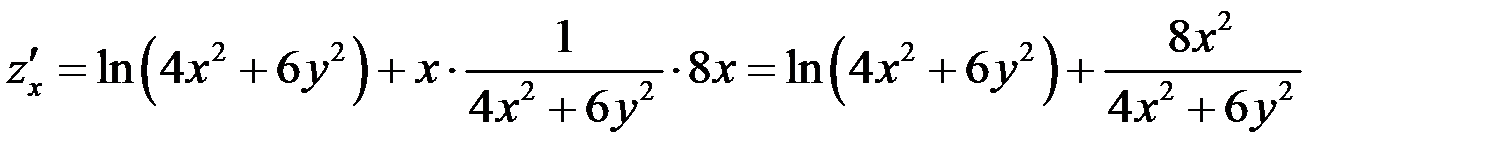 ,
,
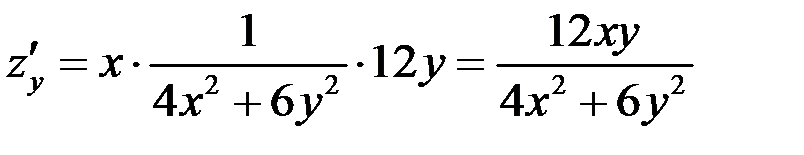 .
.
Подставим найденные выражения в левую часть уравнения:
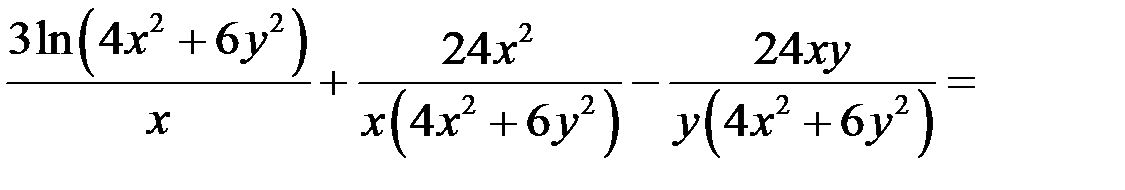
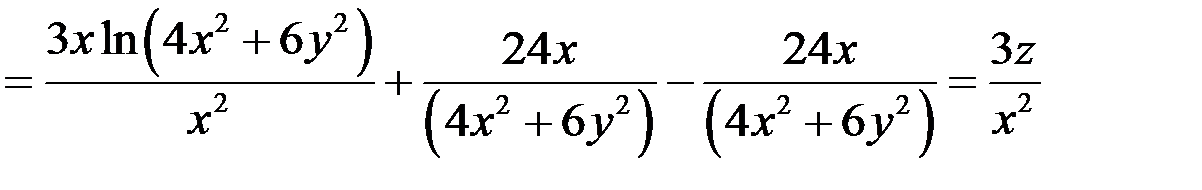 что и требовалось доказать.
что и требовалось доказать.
Пример 1
Найти частные дифференциалы функции
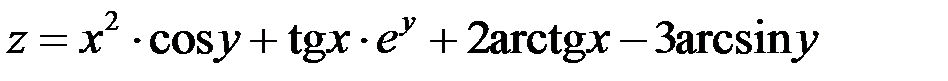
Решение
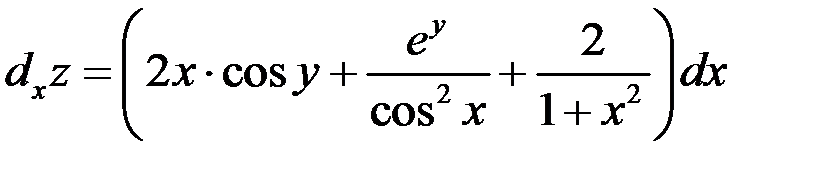 ,
, 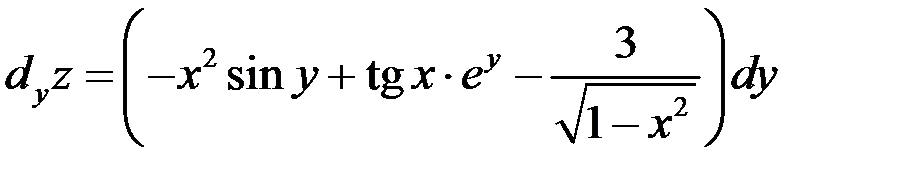 .
.
Полный дифференциал функции 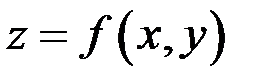 равен сумме ее частных дифференциалов:
равен сумме ее частных дифференциалов:
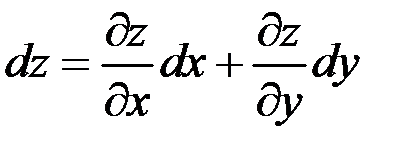 .
.
Пример 2
Найти дифференциал 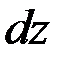 функции
функции 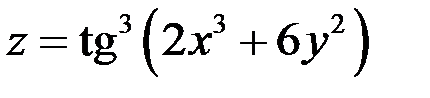 .
.
Решение
Найдем частные производные
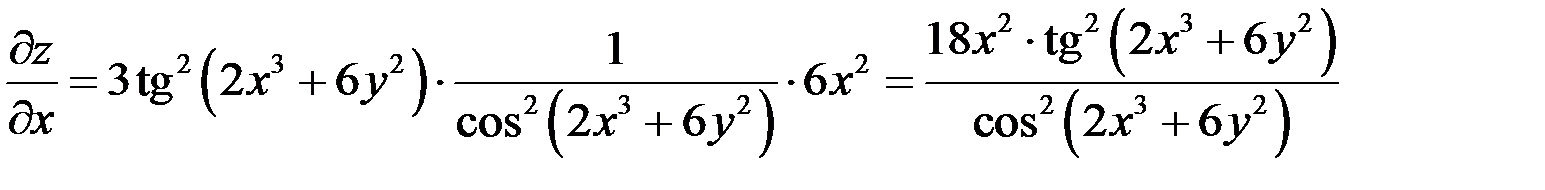 ,
,
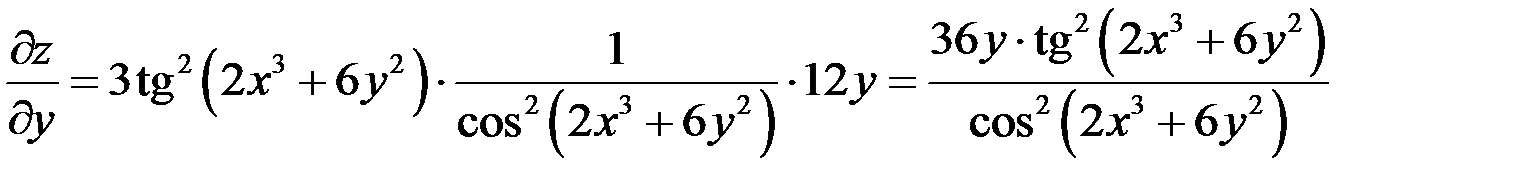 .
.
Подставим частные производные в формулу полного дифференциала, получим
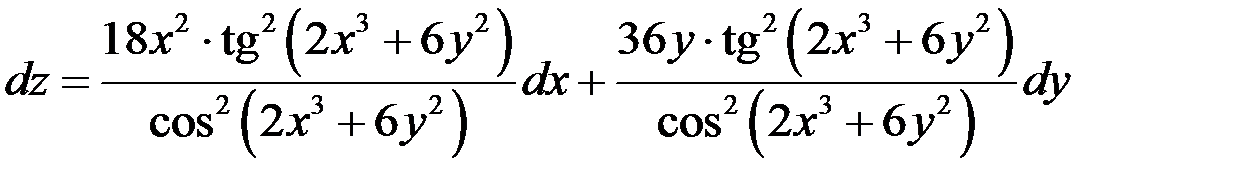 .
.
Пример
Составить уравнения касательной плоскости и нормали к поверхности 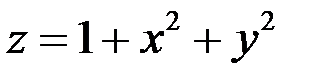 в точке
в точке 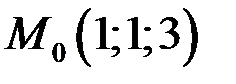 .
.
Решение
Найдем частные производные 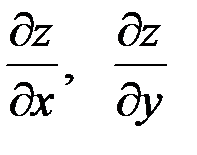 и вычислим их значения в точке
и вычислим их значения в точке 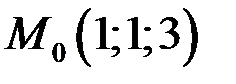 :
:
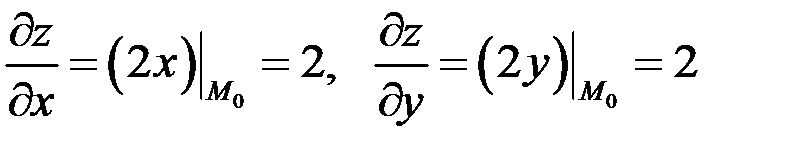 .
.
Уравнение касательной плоскости:
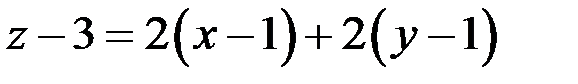 или
или 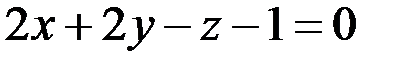 .
.
Уравнение нормали:
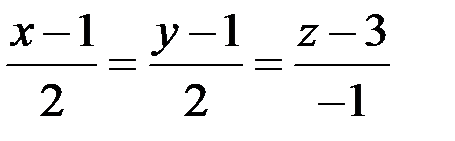 .
.
Пример
Для функции 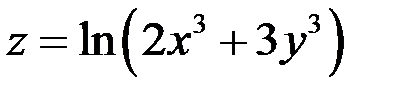 в точке
в точке 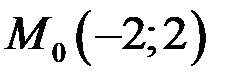 найти градиент и производную по направлению
найти градиент и производную по направлению 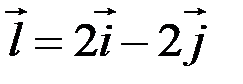 .
.
Решение
Градиент находим по формуле 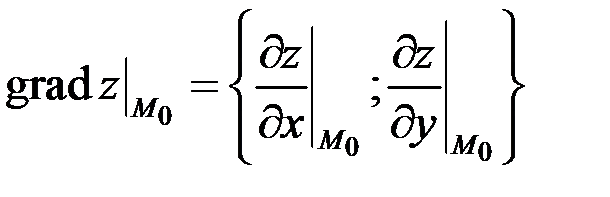 , где
, где
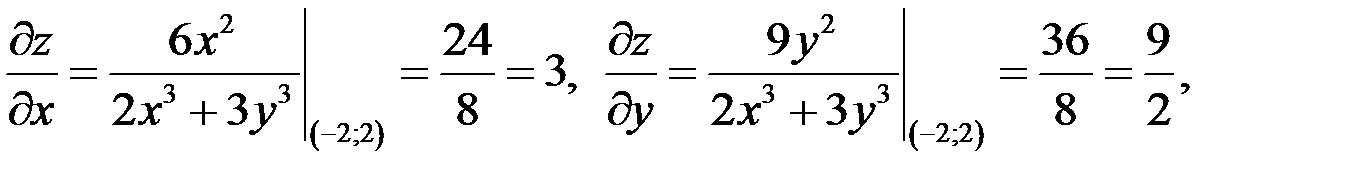 тогда
тогда
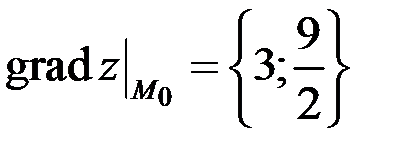 .
.
Производная по направлению: 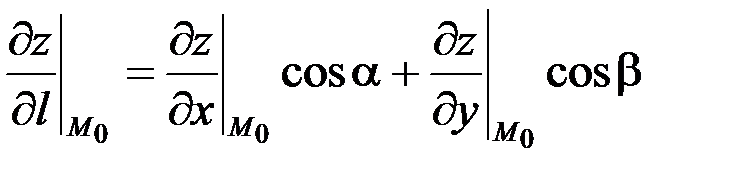 ,
,
где 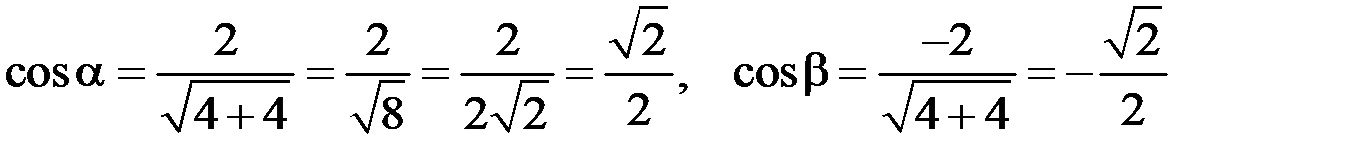 , тогда
, тогда
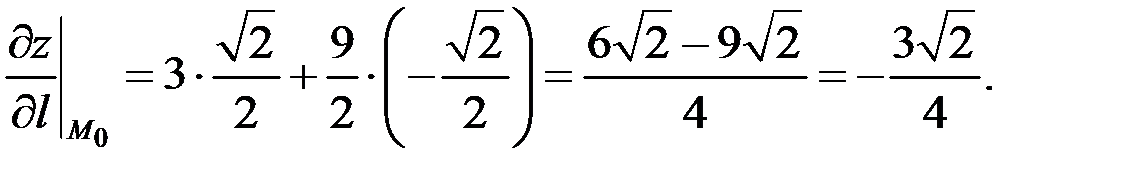
Краткое содержание (программа) курса
Элементы линейной алгебры
Матрицы, операции над ними. Определители и их свойства и вычисление. Ранг матрицы, обратная матрица. Теорема Кронекера-Капелли. Решение систем линейных алгебраических уравнений по формулам Крамера, матричным методом и методом Гаусса. Система m линейных уравнений с n неизвестными.
Кафедра «Прикладная информатика и математика»
МАТЕМАТИКА
Методические указания
по контрольным работам для студентов
заочного отделения
Санкт-Петербург
2015
Одобрено на заседании кафедры «Прикладная информатика и математика»
протокол № ___ от ________ 2015 г.
Сборник заданий по математике. Методические указания по выполнению контрольных работ по курсу «Математика » для студентов заочного отделения.
Сборник содержит задачи контрольных работ по математике для студентов заочного отделения всех направлений, предусмотренные учебной программой в соответствии с ФГОС ВО. Задания и методические указания могут быть использованы в курсах математических дисциплин всех направлений и специальностей СПб УУиЭ.
Составитель:
к.п.н., доцент С.Д. Прозоровская
к.э.н. Т.А. Черняк
Рецензент:
Санкт-Петербургский университет управления и экономики
2015
ОГЛАВЛЕНИЕ
1. Требования к оформлению контрольных работ………..……..….…4
2. Формирование исходных данных к задачам………………….…..…4
3. Рекомендуемая литература…………………….……………………..5
4. Контрольная работа № 1. Линейная алгебра……………………..…6
5. Контрольная работа № 2. Элементы векторной алгебры и аналитической геометрии……………………………………………………24
6. Контрольная работа № 3. Предел и производная функции одной переменной……………………………………………………….….35
7. Контрольная работа № 4. Интегральное исчисление функции одной переменной…………………………………………………..….50
8. Контрольная работа № 5 Дифференциальное исчисление функции нескольких переменных……………………………………………57
9. Краткое содержание (программа) курса…………………….…….63
Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в отдельной тетради. На обложке тетради необходимо указать: название института Университета; название кафедры; название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и личный шифр студента.
2. На каждой странице следует оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.
3. Условия задач переписывать полностью необязательно, достаточно указать номера задач по данному сборнику. В условия задач следует сначала подставить конкретные числовые значения параметров т и п, после чего выполняется их решение.
4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.
Дата: 2019-02-02, просмотров: 397.