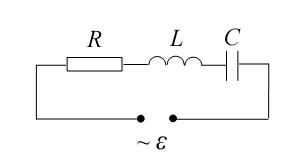
Перейдем теперь к анализу полной электрической цепи с последовательно включенными активным сопротивлением R, индуктивность L и емкостью С, исследуемой в данной работе (рис. 12).

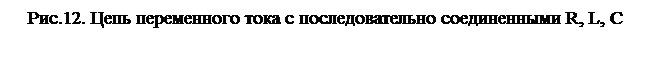
Пусть ЭДС в цепи меняется по гармоническому закону: 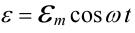                                                                                                (24)

В результате чего в цепи потечет электрический ток:

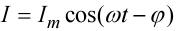                                                            (25)

Определим амплитуду I_m и сдвиг фаз 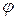 между током и внешней ЭДС, если известны параметры цепи R, L, C. На основании второго закона Кирхгофа для данной цепи запишем:

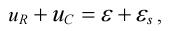                                                                       (26)

Т. е. сумма падений напряжений на отдельных элементах контура равна в каждый момент времени сумме ЭДС, действующих в контуре.

Для любого момента времени t справедливы следующие соотношения:

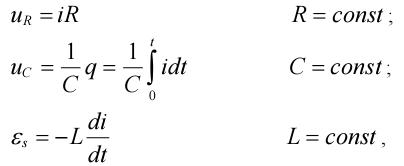
где R – сопротивление резистора, С- емкость конденсатора, L – индуктивность катушки, u_R и u_C – напряжения на соответствующих элементах цепи, i- ток в цепи, q – заряд конденсатора, 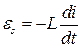 - ЭДС самоиндукции, возникающая в катушке индуктивности при прохождении через неё переменного тока. Подставим (27), (28), (29) в (26).

Получим: 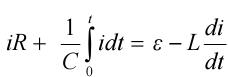. Следовательно:

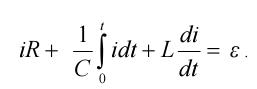                                                (30)

Далее, подставляя в (30) выражения (24) (25):

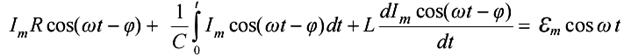
После выполнения операций интегрирования и дифференцирования получим:

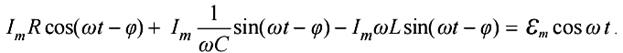
Воспользуемся известными тригонометрическими соотношениями:

преобразуем выражение к окончательному виду:

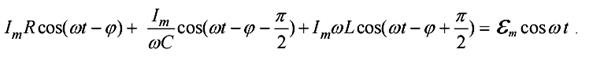(31)

Из анализа (31) можно сделать следующие выводы:

Напряжение на резисторе u_R совпадает по фазе с током в цепи i.

Напряжение на ёмкости u_C отстает по фазе от тока i на угол .

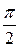Напряжение на индуктивности u_L опережает ток i на угол .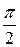

Из этого же уравнения следует, что:

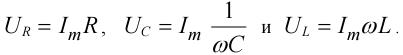                              (32)

Уравнение (31) позволяет определить амплитуду результирующего тока 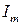, сдвиг фаз между током в цепи и изменением внешней ЭДС, а также полное сопротивление цепи Z, изображенной на рис. 10.

Учитывая уравнения (32) перепишем (31) в виде:

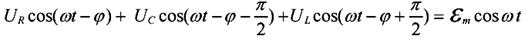(33)

Далее, используя метод векторных диаграмм, представим каждое слагаемое (33) в виде векторов 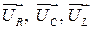и .

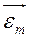Запишем это уравнение как сумму трех векторов, каждый из которых описывает изменение напряжения на резисторе, емкости и индуктивности соответственно:

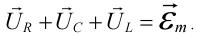
Так как R, L и C соединены последовательно, то через них протекает одинаковый по величине ток, поэтому в качестве основной оси отсчёта на векторной диаграмме выберем ось токов. Тогда, учитывая сдвиги фаз, возникающие между током и напряжениях на ёмкости и индуктивности, векторная диаграмма для нашей цепи будет иметь вид рис. 13. 

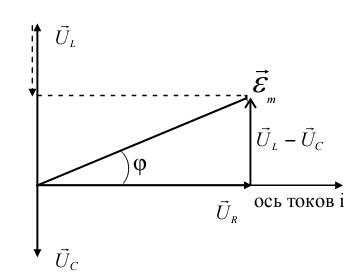
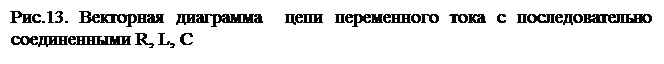
Из рис. 9. по теореме Пифагора имеем:

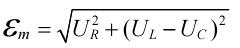
или

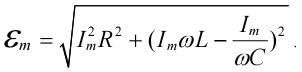
Вынося I за знак корня получим:

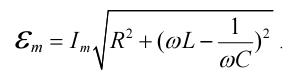
Таким образом, окончательно имеем:

Величина 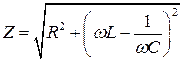 называется полным сопротивлением электрической цепи или импедансом 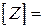Ом. Сдвиг фаз  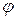между внешней ЭДС генератора и силой тока i можно найти из векторной диаграммы рис. 10: