Мгновенными значениями силы тока i, напряжения u, ЭДС и мощности p в цепях переменного тока называют их значения в данный момент времени.

Амплитудными значениями силы тока I _m, напряжения U _m , ЭДС 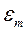  и мощности P_m в цепях переменного тока называют наибольшие мгновенные значения этих величин в случае синусоидального переменного тока за период.

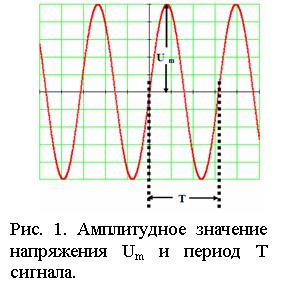
Периодом T называется наименьший промежуток  времени, через который переменный ток повторяет свои значения в той же самой последовательности (рис. 1).

Частотой 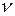 переменного периодического тока называется величина обратная периоду:  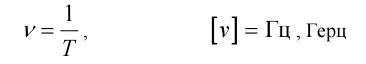                                                                                                                          (2)

Циклической или круговой частотой называют величину:

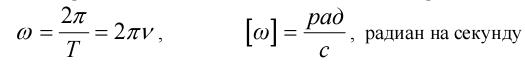       (3)

Сила тока и напряжение переменного тока непрерывно изменяются по величине, поэтому возникла необходимость каким-либо образом сравнивать различные токи друг с другом. При этом необходимо использовать такое действие переменного тока, которое бы не зависело от его направления. В этом отношении наиболее удобным оказалось тепловое действие тока. Причём по тепловому действию тока можно сравнивать переменные токи с постоянными. В связи с этим возникло понятие эффективного значения переменного тока.

Эффективным (действующим, среднеквадратичным) значением переменного тока I_эфф называется такая величина силы постоянного тока, который оказывал бы в цепи такое же тепловое воздействие за время одного периода. По определению:

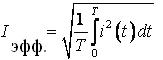
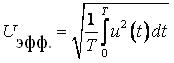                           (4)

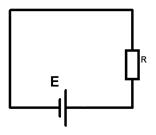
Поясним запись формулы (4). Пусть резистор R подключен к источнику постоянного напряжения, например батареи E (рис. 2). В течение времени T, равное периоду переменного напряжения в нем выделится количество теплоты равное:

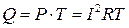                                                        (5)

Подключим теперь этот резистор в цепь переменного тока. Количество теплоты, выделенное переменным током за время dt  равно dQ:

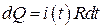
а за период T:

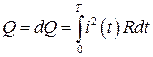                          (6)

Приравнивая (6) и (5) получим:

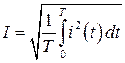
Для синусоидального тока рис. 1, проводя интегрирование, получим:

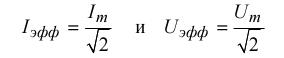                                        (7)

Как правило, все измерительные приборы в электрических цепях отградуированы в действующих значениях величин.

Все элементы электрической цепи обладают сопротивлением. Различают два вида сопротивления: активное и реактивное. Если при прохождении тока через элемент цепи происходит только необратимое превращение электрической энергии в теплоту, то сопротивление такого участка цепи называют активным. Если такого превращения не происходит, то сопротивление называют реактивным. 

Элемент цепи с активным сопротивлением называется резистором. Реактивным сопротивлением – емкостным и индуктивным – обладают соответственно конденсаторы и катушки индуктивности.

Наличие реактивных сопротивлений в цепи переменного тока приводит к тому, что возникает разность фаз между изменениями напряжения и тока в цепи (то есть ток и напряжение не одновременно достигают своего максимального значения). Это обстоятельство значительно усложняет расчёты цепей переменного тока.

Сопротивлением участка цепи постоянного тока называют величину равную:

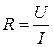                                                                                       (8)

Сопротивлением участка цепи переменного тока называют величину равную:

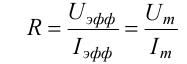                                                          (10)

Математическое описание переменного тока можно осуществить тремя методами: 

- аналитический метод (с помощью тригонометрических функций),

- символический метод (с помощью комплексных чисел),

- метод векторных диаграмм (используется графический метод описания переменного тока).

Аналитический метод описания синусоидальных токов  иногда приводит к громоздким математическим преобразованиям при определении каких-либо величин. Поэтому для упрощения расчётов в этих случаях были придуманы другие методы вычислений, которые мы сейчас рассмотрим.

Метод векторных диаграмм

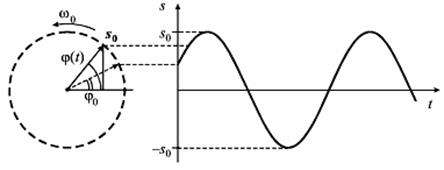
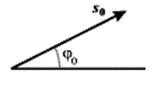
Гармонические колебания допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой 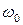можно поставить в соответствие вращающийся с угловой скоростью 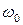вектор, длина которого равна амплитуде  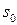а его начальное (стартовое) положение задается углом 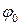совпадающим с начальной фазой (рис. 3).

Вертикальная проекция вектора 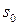 изменяется со временем:

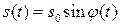                                                                               (11)

 Мгновенное положение вектора 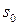определяется углом  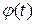- фазой:

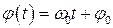                                                                         (12)

При угловой скорости (круговой частоте) 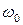вектор совершает  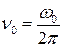оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла 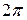к угловой скорости : .

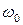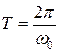С помощью векторных диаграмм легко осуществить сложение гармонических колебаний. Так, если необходимо сложить два гармонических колебания с одинаковыми частотами:

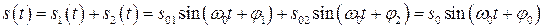(13)

то амплитуду 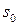 и начальную фазу 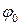суммарного колебания 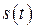с той же частотой  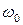можно легко рассчитать из рис. 4а, на котором графически изображена операция сложения векторов 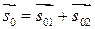в момент времени t=0.

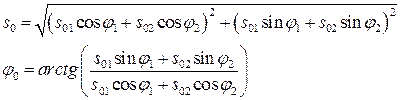                (14)

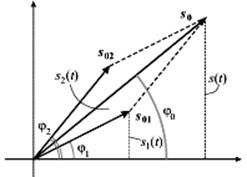
Ясно, что вертикальная проекция вектора 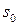будет также изменяться по гармоническому закону с частотой 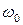поскольку взаимное расположение векторов 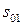и 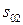не изменяется с течением времени.

Из этой диаграммы наглядно видно, что суммарное колебание опережает по фазе колебание и отстает по фазе от колебания 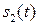. Полная фаза для каждого из трех колебаний в произвольный момент времени отличается от их начальных фаз на одну и ту же величину 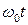которую при построении векторных диаграмм не учитывают. При этом колебание изображается неподвижным вектором (рис. 4б), а частота колебания предполагается известной.

Этот метод очень удобен при сложении двух или нескольких гармонических колебаний, так как в этом случае громоздкие тригонометрические преобразования можно заменить простым сложением векторов.

 Используя идеи этого метода, для различных цепей синусоидального тока строят свои диаграммы, на которых одновременно в виде векторов изображают напряжения и токи в цепи, а по ним определять сдвиг по фазе между изменениями тока и напряжения, а также ряд других характеристик цепи.