МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Кафедра ПР-3 «Медицинские приборы и компьютерные технологии»
УТВЕРЖДАЮ
И.о. заведующего
кафедрой ПР-3
_________/Гренков В.Л/
«___»_________2012 г.
для студентов специальности
Биотехнические и медицинские аппараты и системы»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
НА ЛАБОРАТОРНЫЕ ЗАНЯТИЯ №1-4
по дисциплине 2325 «Воздействие физических полей на биообъекты»
Обсуждены на заседании кафедры
«__»___________2012 г.
Протокол № __
МГУПИ – 2012г.
1. Время каждого занятия: 4 часа (акад.)
2. Место проведения: Проблемная лаборатория молекулярной акустики
Лабораторная работа №1
Измерение импеданса биологического объекта.
Измерение импеданса электрической цепи переменного тока. Проверка закона Ома для цепи переменного тока.
Цель работы: изучение цепей переменного тока, экспериментальная проверка закона Ома для цепи переменного тока с последовательно соединенным активным сопротивлением, емкостью и индуктивностью; экспериментальное получение зависимости сопротивлений от частоты переменного тока: индуктивного - 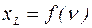 , емкостного -
, емкостного - 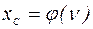 , биологической ткани -
, биологической ткани - 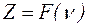 ; производить соответствующие расчеты и по графику функциональной зависимости импеданса биообъекта от частоты переменного тока оценивать его активное сопротивление.
; производить соответствующие расчеты и по графику функциональной зависимости импеданса биообъекта от частоты переменного тока оценивать его активное сопротивление.
Теоретическое описание.
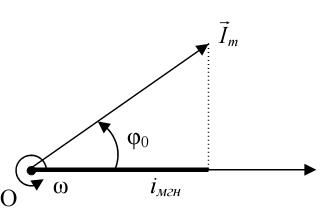
Метод векторных диаграмм
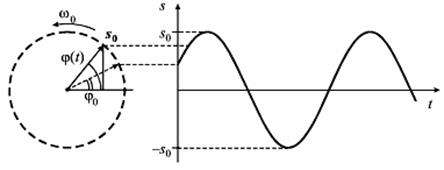
Гармонические колебания допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой 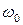 можно поставить в соответствие вращающийся с угловой скоростью
можно поставить в соответствие вращающийся с угловой скоростью 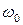 вектор, длина которого равна амплитуде
вектор, длина которого равна амплитуде 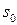 а его начальное (стартовое) положение задается углом
а его начальное (стартовое) положение задается углом 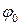 совпадающим с начальной фазой (рис. 3).
совпадающим с начальной фазой (рис. 3).
Вертикальная проекция вектора 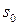 изменяется со временем:
изменяется со временем:
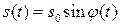 (11)
(11)
Мгновенное положение вектора 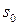 определяется углом
определяется углом 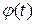 - фазой:
- фазой:
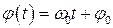 (12)
(12)
При угловой скорости (круговой частоте) 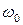 вектор совершает
вектор совершает 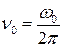 оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла
оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла 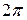 к угловой скорости
к угловой скорости 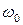 :
: 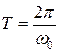 .
.
С помощью векторных диаграмм легко осуществить сложение гармонических колебаний. Так, если необходимо сложить два гармонических колебания с одинаковыми частотами:
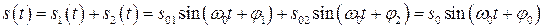 (13)
(13)
то амплитуду 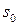 и начальную фазу
и начальную фазу 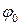 суммарного колебания
суммарного колебания 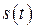 с той же частотой
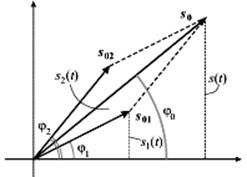
с той же частотой 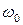 можно легко рассчитать из рис. 4а, на котором графически изображена операция сложения векторов
можно легко рассчитать из рис. 4а, на котором графически изображена операция сложения векторов 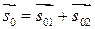 в момент времени t=0.
в момент времени t=0.
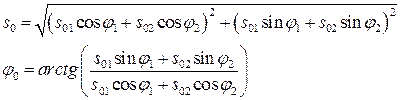 (14)
(14)
|
|
|
Ясно, что вертикальная проекция вектора 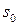 будет также изменяться по гармоническому закону с частотой
будет также изменяться по гармоническому закону с частотой 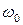 поскольку взаимное расположение векторов
поскольку взаимное расположение векторов 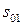 и
и 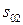 не изменяется с течением времени.
не изменяется с течением времени.

Из этой диаграммы наглядно видно, что суммарное колебание 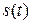 опережает по фазе колебание
опережает по фазе колебание 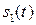 и отстает по фазе от колебания
и отстает по фазе от колебания 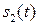 . Полная фаза для каждого из трех колебаний в произвольный момент времени отличается от их начальных фаз на одну и ту же величину
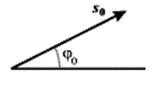
. Полная фаза для каждого из трех колебаний в произвольный момент времени отличается от их начальных фаз на одну и ту же величину 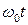 которую при построении векторных диаграмм не учитывают. При этом колебание изображается неподвижным вектором (рис. 4б), а частота колебания предполагается известной.
которую при построении векторных диаграмм не учитывают. При этом колебание изображается неподвижным вектором (рис. 4б), а частота колебания предполагается известной.
Этот метод очень удобен при сложении двух или нескольких гармонических колебаний, так как в этом случае громоздкие тригонометрические преобразования можно заменить простым сложением векторов.
Используя идеи этого метода, для различных цепей синусоидального тока строят свои диаграммы, на которых одновременно в виде векторов изображают напряжения и токи в цепи, а по ним определять сдвиг по фазе между изменениями тока и напряжения, а также ряд других характеристик цепи.
Виды поляризаций.
Электронная поляризация - наиболее общий вид поляризации представляет собой смещение электронов на своих орбитах относительно положительно заряженных ядер в атомах и ионах. В результате такого смещения атом или ион превращается в индуцированный диполь с направлением, противоположным внешнему полю. Время возникновения поляризации после мгновенного наложения поля, называется временем релаксации. Оно составляет в данном случае 10-16- 10-14 с.
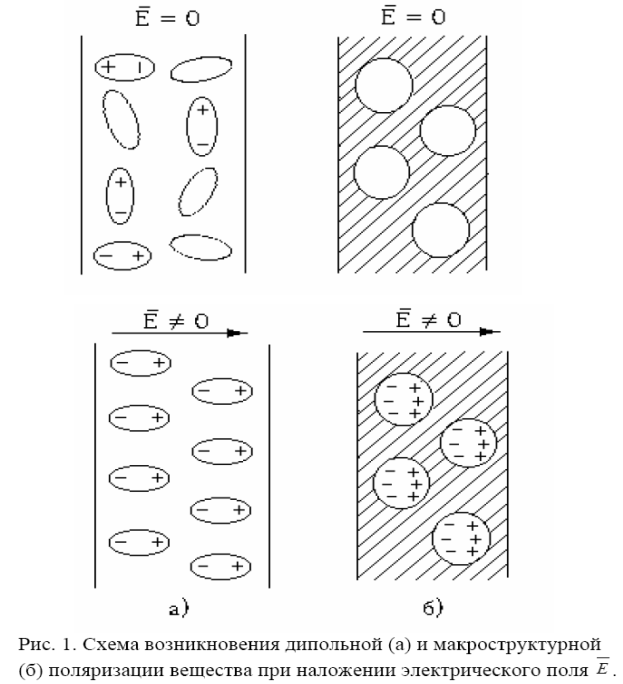
Дипольная (ориентационная) поляризация типична для многих жидкостей и газов (вода, спирты, нитробензол). Молекулы этих полярных диэлектриков не симметричны: “центры масс” их положительных и отрицательных зарядов не совпадают и молекулы обладают дипольным моментом. Дипольные моменты отдельных молекул в отсутствие электрического поля ориентированы хаотически, а во внешнем электрическом поле приобретают преимущественную ориентацию вдоль поля (рис. 14а).
Значительными дипольными моментами вследствие диссоциации ионных групп, а также вследствие адсорбции ионов обладают молекулы белков и других высокомолекулярных соединений. Поэтому в растворах этих веществ дипольная поляризация, обусловленная вращением их полярных молекул, имеет большое значение. Время релаксации дипольной поляризации изменяется в пределах от 10-13- 10-7 с.
Макроструктурная поляризация возникает под действием электрического поля вследствие неоднородности электрических свойств вещества. Для ее возникновения необходимо наличие слоев с различной электропроводностью. Под действием поля свободные ионы и электроны, содержащиеся в проводящих субстанциях, перемещаются в пределах каждого включения до границы проводящего слоя. Дальнейшее перемещение свободных зарядов невозможно вследствие низкой проводимости соседних слоев (рис. 14б). В результате этого процесса проводящее включение приобретает дипольный момент и ведет себя подобно гигантской полярной молекуле. Этот вид поляризации играет основную роль в биологических объектах, являющихся гетерогенными структурами. Гетерогенность тканей в большой степени обусловлена наличием мембран. К ним относятся клеточные мембраны и мембраны, окружающие клеточные органоиды и образующие эндоплазматическую сеть.
Цитоплазма клеток обладает малым активным сопротивлением из-за наличия в ней большого количества свободных ионов, в то время как у мембран вследствие их малой проницаемости для ионов, оно очень высокое (примерно 1000 Ом на каждый см2 площади поверхности мембраны).
|
Поверхностная поляризация происходит на поверхностях, имеющих двойной электрический слой. При наложении внешнего электрического поля происходит перераспределение ионов диффузной части двойного электрического слоя: частицы дисперсной фазы смещаются в одну сторону, а ионы диффузного слоя - в другую. В результате частицы дисперсной фазы с противоионами диффузного слоя превращаются в наведенные диполи. Время релаксации поверхностной поляризации лежит в пределах от 10-3 до 1 с.
Электролитическая поляризация возникает между электродами, опущенными в раствор электролита, при протекании через них электрического тока. При наложении разности потенциалов на электроды произойдет перераспределение потенциалов, определяющих ионов в диффузной части двойного электрического слоя. В области катода увеличится концентрация катионов, а в области анода - уменьшится. Следовательно, и в данном случае появление поляризации обусловлено смещением зарядов, которое проявляется в изменении концентрации ионов в приэлектродной области. Время релаксации электролитической поляризации имеет порядок 10-4 – 10-2 с.
Все описанные виды поляризации в той или иной степени присущи биологическим объектам.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Порядок выполнения
ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА.
1. Перед началом работы ознакомится с принципиальными схемами установки, разобраться в назначении ручек и кнопок учебного модуля. Проверить целостность сетевого провода.
2. Включить установку в сеть ~220 В. Поставить переключатель «СЕТЬ» в положение «ВКЛ» при этом должен загореться сигнальный индикатор «сеть».
3. Многофункциональная кнопка «ГЕНЕРАТОР/R,f /U» перед началом эксперимента должна быть отжата, генератор выключен.
4. Пользуясь интерактивным меню, отображаемом на дисплее прибора, выбрать необходимый эксперимент (обычно первый опыт — Изучение импеданса электрической цепи переменного тока « IMPED RLC »).
5. Для перемещения по пунктам меню служит кнопка «ВЫБОР ОПЫТА». Текущее положение отображается на дисплее символом «*». Для начала эксперимента нажать кнопку «ENTER».
6. Установить одну из частот генератора с помощью кнопок «ЧАСТОТА». Для надежного срабатывания кнопок их необходимо удерживать нажатыми в течение не менее 2-х секунд.
7. Установить переменный резистор «R» (активное сопротивление) в среднее положение. Занести значение R и частоты ν в табл. 1.
8. Нажатием кнопки «ГЕНЕРАТОР/R,f/U» включить вольтметры, измеряющие падения напряжений на катушке индуктивности и резисторе R. Ручку R при этом не трогать (в любом режиме работы, вращение ручки R приводит к изменению активного сопротивления) Занести измеренные данные в таблицу 1.
9. Переключить установку кнопкой «UR, UL / UR, UC» для точного измерения падения напряжения на конденсаторе (падение напряжение на резисторе, естественно не изменяется). Занести измеренные значения в табл.1
10. Рассчитать по формулам (32) действующее значение электрического тока в цепи, значения индуктивного и емкостного сопротивления, а также значения емкости конденсатора и индуктивности катушки самоиндукции. Следует помнить, что вольтметры измеряют действующие значения напряжения, в формулы же (32) входят амплитудные значения. Однако, согласно (7), действующие и амплитудные значения различаются только постоянным множителем и (32) можно также использовать для действующих значений без изменений (подставляя показания вольтметров, получаем не Im а Iдейст). При расчетах считать все элементы цепи идеальными.
11. Отжать кнопку «ГЕНЕРАТОР/R,f/U» и установить другое значение активного сопротивления R, не изменяя частоты генератора. Записать R в таблицу 1.
12. Повторить действия пп. 8 - 11. Все рассчитанные и измеренные данные занести в таблицу.
13. Устанавливая кнопками «ЧАСТОТА», другие значения частоты генератора, провести аналогичные измерения для еще каких-либо двух-трех частот и двух- трех значений активной нагрузки R.
14. Рассчитать средние значения индуктивности <L> и емкости <C>.
15. По формулам 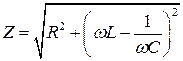 рассчитать импеданс электрической цепи для частот
рассчитать импеданс электрической цепи для частот 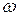 и активных сопротивлений R, при которых вы проводили измерения. Все вычисления производите в СИ. Данные занести в табл. 1
и активных сопротивлений R, при которых вы проводили измерения. Все вычисления производите в СИ. Данные занести в табл. 1
16. Сравните рассчитанные вами значения емкости С и индуктивности L с реальными значениями этих параметров для данной установки:
C =10 нФ; L =0,47 Гн
Таблица 1
|
| R, Ом | UR, В | UC, В | UL, В | C, нФ | L, Гн | Z, Ом |
|
| |||||||
<L>=… Гн, <C>=… нФ
17. Проверить справедливость закона Ома для цепи переменного тока. Рассчитать для нескольких частот 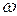 и значений импеданса Z действующее значение ЭДС
и значений импеданса Z действующее значение ЭДС 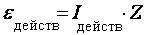 с выхода генератора G и сравнить его с реальным значением для данной установки
с выхода генератора G и сравнить его с реальным значением для данной установки 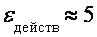 Вольт.
Вольт.
18. По окончании эксперимента нажать кнопку «ESC» и перейти в главное меню выбора опыта.
Второй эксперимент. Определение зависимости импеданса биологического объекта от частоты переменного тока и его активного сопротивления RT
19. При помощи кнопки «ВЫБОР ОПЫТА» выбрать второй эксперимент «Измерение импеданса биологического объекта» «IMPED BIOLOGY» и войти в режим измерения, нажав кнопку «ENTER».
20. Установить частоту встроенного звукового генератора установки равной 1 кГц с помощью ручки «ЧАСТОТА».
21. Записать измеренное значение полного сопротивления образца Z, Ом и частоту тока воздействия F, кГц в таблицу 2.
22. Установливая ручкой «ЧАСТОТА» другие частоты звукового генератора, снять зависимость полного электрического сопротивления образца в норме (режим NORMAL) от частоты Z=Z(f). Все измеренные данные занести в таблицу 2.
Таблица 2
| Частота тока воздействия, F, кГц | ||||
| Полное сопротивление объекта исследования, Z, Ом |
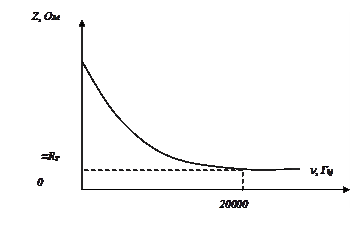
23.  Постройте по полученным данным график зависимости импеданса биологического образца от частоты тока воздействия Z=Z(ν) на миллиметровке. График должен иметь вид, аналогичный рисунку 30.
Постройте по полученным данным график зависимости импеданса биологического образца от частоты тока воздействия Z=Z(ν) на миллиметровке. График должен иметь вид, аналогичный рисунку 30.
24. По полученному графику оценить активное сопротивление ткани Rт, как величину сопротивления, не меняющегося с изменением частоты. Импеданс ткани 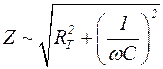 , где RT – активное сопротивление ткани (RT – const на всех частотах в данных условиях),
, где RT – активное сопротивление ткани (RT – const на всех частотах в данных условиях), 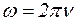 . Например, по графику рис. 30 можно установить, что при частоте
. Например, по графику рис. 30 можно установить, что при частоте 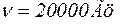 величина
величина 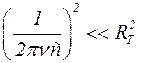 , поэтому
, поэтому 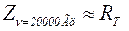 . Таким образом, за активное сопротивление биологической ткани RT в данном случае приблизительно принимаем значение импеданса Z при частоте
. Таким образом, за активное сопротивление биологической ткани RT в данном случае приблизительно принимаем значение импеданса Z при частоте 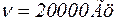
25. С помощью многофункциональных кнопок «ВЫБОР ОПЫТА/ЧАСТОТА/СОСТОЯНИЕ ОБРАЗЦА» выбрать состояние образца после кипячения в течение 2 минут (BIOL 2), а затем 5 минут (BIOL 5) при отмирание биологического объекта и повторить пп. 21 – 25.
26. Сравнить полученные вами зависимости с теоретическими графиками рис. 16 и сделать выводы.
27. По окончании работы выключить установку, поставив переключатель «СЕТЬ» в положение «выкл», при этом должен погаснуть сигнальный светодиод «сеть» и вынуть сетевую вилку из розетки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется переменным электрическим током?
2. Перечислите основные характеристики переменного тока.
3. Что называется действующим значением напряжения, тока, ЭДС? Каковы эти значения при синусоидальном токе? Выведите формулу (7) для действующих значений.
4. Перечислите основные методы вычислений для цепей переменного тока.
5. Из рисунка 4 выведите формулу (14) для сложения гармонических колебаний. Объясните построение векторной диаграммы.
6. Чему равен сдвиг фаз между током и напряжением в цепочках R, L и R, C? Построить векторные диаграммы.
7. Чему равны индуктивное и емкостное сопротивления? Как они изменяются с частотой?
8. Рассмотрите цепь на рис. 10 и выведите закон Ома для нее.
9. Что называется импедансом электрической цепи? Что произойдет, если при некоторой частоте генератора ω0 в электрической цепи рис. 10 значения индуктивного и емкостного сопротивлений сравняются по величине? Изобразите этот случай на векторной диаграмме.
10. Дайте определение диполя, дипольного момента, плеча диполя. Как они направлены в электрическом поле? Вне его?
11. Перечислите виды поляризации и дайте их краткую характеристику.
12. Чем обусловлены емкостные свойства живой ткани?
13. Каковы особенности электропроводности биологических объектов?
14. Чем обусловлены емкостные свойства биологических тканей?
15. Что такое дисперсия импеданса?
16. Расскажите о применении метода измерения электропроводности
в медицине и биологии.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Практикум по физике. Электричество и магнетизм: уч. пособ. для вузов / под ред. Ф. А. Николаева – М.: Высш. шк., 1991. – 151 с.
2. Савельев И. В. Курс общей физики. Т. 2 / И. В. Савельев – М.: Наука, 1988. – 496 с.
3. Детлаф А. А. Курс физики / А. А. Детлаф, Б. М. Яворский – М.: Высш. шк., 1989. – 608 с.
4. Бордовский Г.А. Общая физика: курс лекций с компьютерной поддержкой. Т. 1. / Г.А. Бордовский, Э. В. Бурсиан – М.: Изд-во Владос-Пресс, 2001. – 240 с.
5. Кошкин Н. И. Справочник по элементарной физике / Н. И. Кошкин, М. Г. Ширкевич – М.: Наука, 1988. – 284 с.
6. Калашников С.Г. Электричество. - М.: Физматгиз. 1985-1986
7. Губанов Н.И., Утенбергеров А.А. Медицинская биофизика. М.: Медицина, 1978. С. 211-230.
8. Ремизов А.Н. Медицинская и биологическая физика.М.: Высшая школа, 1987. Т. 2. С. 330 - 331.
9. Ливенцев Н.М. Курс физики. М.: Высшая школа, 1978. Т.2. С. 146 - 150.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Дата: 2019-02-02, просмотров: 482.
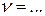 Гц
Гц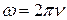 =…
=…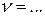 Гц
Гц