Методом конечных разностей

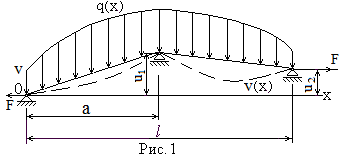Гибкая струна(рис. 1)лежит на трёх опорах, находящихся на разных уровнях к горизонту, туго натягивается

продольной силой F, постоянной по всей длине, нагружена неравномерной распределённой нагрузкой

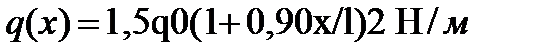
Её изогнутая ось описывается обыкновенным дифференци-альным уравнением второго порядка

    Требуется найти методом конечных разностей сеточную функцию v(x_i) и изобразить её график.

Исходные данные

Решение

Продольную силу представим в виде

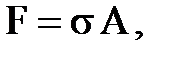
где 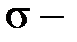 нормальное напряжение в поперечном сечении, А – площадь поперечного сечения. Перепишем (1) в виде

                                       (1)

Здесь введено обозначение

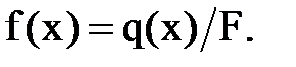
К уравнению (1) присоединяются граничные условия на концах струны

(2)

соответствующие факту их неподвижности, и условие на промежуточной опоре

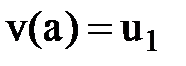.                                           (3)

Задачу (1) - (3) далее будем решать с помощью метода конечных разностей. С этой целью вместо подобласти L + Г введём дискретную область l_h в виде узлов равномерной сетки с шагом h

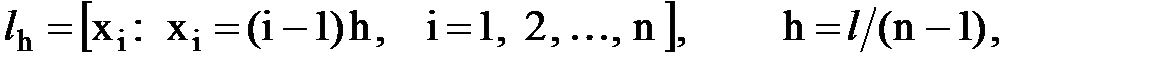
где Г – граница области, n – количество узлов сетки. Значения функций и производной заменим точными и приближёнными значениями в узлах сетки

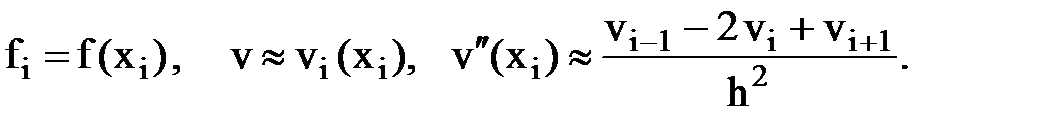
Тогда вместо уравнения (1) и дополнительных условий (2), (3) получим однородную систему линейных алгебраических уравнений

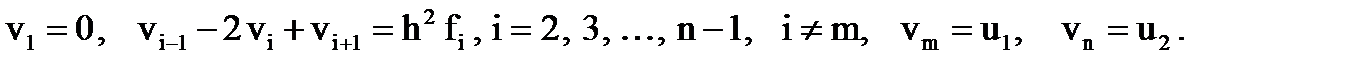
Здесь m – номер точки, совпадающей со средней опорой. Систему уравнений можно переписать в матрично-векторной форме

Bv = с,                                              (6)

где B - квадратная матрица порядка n, v^T = {v₁, v₂,…, v_n} – вектор, компонентами которого являются отклонения струны.

Можно легко показать, что матрица коэффициентов является ленточной и трёхдиагональной вида

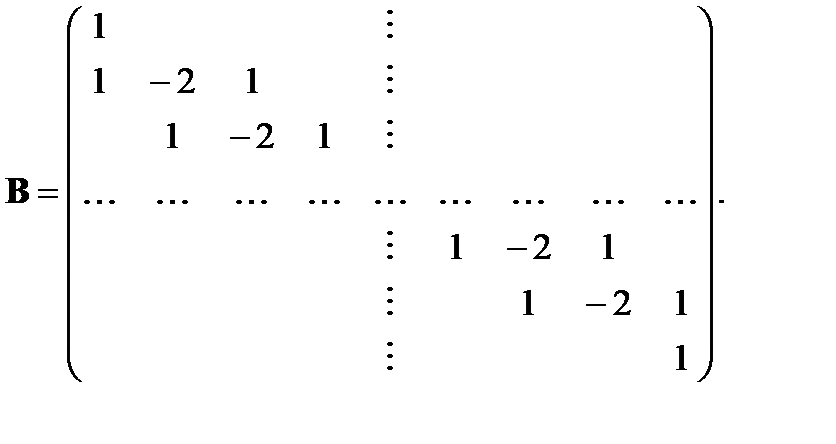
Здесь нулевые элементы не выписаны. Правая часть системы уравнений является вектором

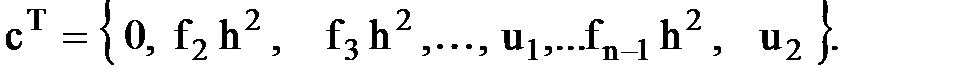
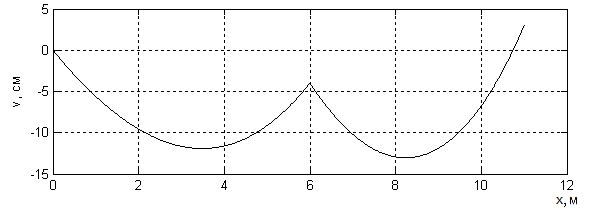
Задача решена с помощью программы на алгоритмическом языке MATLAB. Результаты счёта представлены на рис. 2.

% Струна. Cтатическая задача. 11.12.18

% Отклонения струны. Метод конечных разностей.

% Общая постановка задачи:

% v''=f(x), f(x)=q(x)/sig/A, v(0)=0, v(l)=0.

% Приведение к алгебраической системе общего вида

%              B v = c

% и её решение

clearall;

disp ('Начало_____________________')

l=11; a=6; u1=-0.04; u2=0.03; A=0.00004; sig=30e+06; 

n=1001; n1=n-1; h=l/n1; m=round(a/h+1);

 x=[0 : h : l]; q0=11; 

q=1.5*q0*(1+0.90*x/l).^2;

F=sig*A;

f=zeros(1,n); v=zeros(1,n); c=zeros(1,n); B=zeros(n,n);

f=q/F;  

% Формирование матрицы В

B(1,1)=1; B(n,n)=1; % Граничные условия

% В регулярных точках сетки

for i=2:m-1;

B(i,i-1)=1; B(i,i)=-2; B(i,i+1)=1; c(i)=f(i)*h^2;

end;

B(m,m)=1; c(m)=u1;

for i=m+1:n-1;

B(i,i-1)=1; B(i,i)=-2; B(i,i+1)=1; c(i)=f(i)*h^2;

end;

c(n)=u2;

% Решение системы уравнений

v=B\c';

plot (x, v*100, 'k','LineWidth',1), grid on;

xlabel('x'); ylabel('v, cм');

disp ('Конец_____________________')